二阶导数识别井储效应的气井试井解释新方法

田冷，王泽川*，张春阳，王建礼，蒋丽丽

(1.中国石油大学(北京)石油工程学院，北京 102249；2.长庆油田第三采油厂，延安 716000)

近年来，中国天然气需求量不断增长，已成为全球最大的天然气进口国，2018年对外依存度达到45.3%，需求量增速远高于国内产量增速，供需矛盾日益突出[1]。在天然气开采中，试井是动态描述及动态监测的重要手段之一，已成为气田勘探开发工作的重要组成部分[2]。

对气井试井的研究已经开展了很多年，在传统试井模型的基础上，也产生了很多新理论和新方法，李晓平等[3]针对水平气井渗流机理复杂，对不稳定试井难以分析的情况，利用拉氏反演算法，做出了识别和求取流动阶段地层参数的试井分析典型曲线；田冷等[4]针对苏里格气藏非均质性严重的实际情况,建立了既考虑表皮效应、井筒存储效应的影响,又考虑气藏地层特性及地层厚度变化的适合其气藏特征的三区不等厚横向非均质复合气藏试井解释模型,求出了无限大和封闭边界两种典型外边界条件下的气藏拟压力解,并绘制了井底压降典型曲线,就各参数对典型曲线的影响进行了分析；曾杨等[5]通过对双对数图中的拟压力和拟压力导数曲线进行分析,从中找出一些特征点和特征线,推出了计算储层参数的新公式，对未出现径向流的气井试井资料进行了解释。

相比于油井，天然气压缩性强，且气井一般较深，井筒储集效应严重，应用常规理论难以很好地拟合实际试井资料，在试井分析过程中会对试井解释结果的准确性造成较大影响，因此亟须对理论分析方法进行改进，以获得更准确的试井解释结果。

对井筒储集效应的影响已有很多研究，李跃刚等[6]利用压力导数判别方法，确定了受井筒储集效应影响下的半对数直线段起点的判断依据。程时清等[7]考虑了变井筒储集效应对试井的影响，绘制了井筒储集系数呈三种变化形式的典型曲线，并获得了一些规律性的认识。张晓龙[8]对受井储效应影响下的油井的续流现象进行了研究，为产量计量提供了理论依据。刘鹏超等[9]避开了早期实测数据波动的问题，对霍纳曲线直线段进行了分析，从而提出了求取井储系数的新方法。王强等[10]考虑到页岩气的吸附-扩散效应、滑脱效应以及应力敏感效应,重新建立了页岩气藏渗流模型，并考虑了表皮效应和井筒储集效应对产能公式的影响。

现从试井理论入手，针对气井的压恢试井，推导考虑井储效应及表皮系数的试井解释新模型，依据井储效应影响程度划分两种试井解释类型，并运用二阶导数识别不同压恢曲线中的井储效应。对实际测试数据运用有限差分方法，耦合多条曲线拟合结果，提高试井解释的准确性。

1 试井分析模型改进

1.1 气井压恢试井基础模型

压恢试井是气井试井的常用方法，因为关井过程中产量恒为0，结果较为稳定。假设一口井，以稳定产量生产的时间为tp，然后关井进行压力恢复试井，则试井曲线[2]可以描述为

(1)

(2)

式中：k为渗透率，mD；h为储层有效厚度，m；q为产气量，104m3/d；μ为流体黏度，mPa·s；B为气体地层体积系数；t为关井时间，h；pi为原始地层压力，MPa；pws为关井后井底压力，MPa。

以上称为压力恢复公式，如果关井前生产时间比关井时间长很多，即tp≥Δtmax，且考虑气井表皮系数影响，则可得

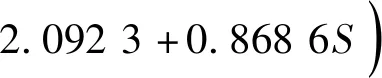
(3)

式(3)中：pwf为井底流动压力，MPa；φ为岩石孔隙度；Ct为储层的综合压缩系数，MPa-1；rw为完井半径，m；pwf为关井时井底压力，MPa；S为表皮系数。

式(3)称为MDH公式，针对长时间生产后关井的气井，如果在直角坐标纸上做出pws(t)和lgt之间的关系曲线，测出其斜率，即可以计算得到各个参数，然而，在实际气井试井分析中，由于井储效应的影响，实测曲线往往偏离趋势线，拟合效果不理想，无法获得准确的测试数据。

在气井生产中，由于井筒具有一定的储容性，井筒中流体具有一定的压缩性，使得井底产量变化滞后于地面产量变化，这种现象称为井筒储集效应。井储效应的井储系数[5]表示为

(4)

由式(4)可以得到，井储效应受流体压缩性影响，而天然气压缩性较强，在试井分析过程中不能忽略。

受井筒储集效应影响，针对压恢试井模型，需要在试井公式中引入井储系数，可得

(5)

定义压力变化为

p(t)=pws(t)-pwf(tp)

(6)

式(6)中：p(t)为仅与关井时间t相关的函数。

化简可得

(7)

定义等效时间为

t′=lgt

(8)

则可得分析方程为

(9)

式(9)难以得到解析解，因此需要利用计算机辅助得到数值解，从而得到压力恢复值p和等效时间lgt之间的关系。

气井受井储效应影响程度不同，压恢曲线表现也不同，针对不同的井储系数，做出其压力恢复值p和等效时间lgt之间的关系图如图1所示。

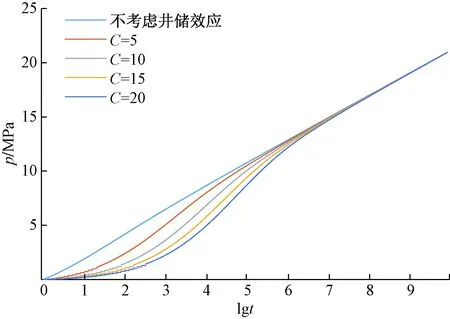
图1 不同井储系数下的压恢试井理论曲线Fig.1 The oretical curves of pressure buildup test under different well storage coefficients

从图1中可以看到，在压恢试井前期，受井储效应影响，压力恢复速度明显下降，p-lgt关系整体呈凹型曲线状态；井储系数越大，试井初期压力恢复速度越慢，在半对数曲线中表现为凹度值增大。

1.2 二阶导数试井分析模型

结合压力恢复曲线和分析方程中压力对等效时间的一阶导数的曲线，可以得到对比图如图2所示。

图2 压力恢复曲线及其一阶导数曲线图Fig.2 Pressure buildup test curve and its first derivative curve

可以明显看到，压恢曲线的斜率呈现增大后减小的关系，针对此模型，可以应用实际试井资料拟合获知方程中各系数，从而得到气井的地层系数、表皮系数等参数，为方便拟合，进一步探究压恢曲线和压恢曲线一阶导数的性质，对压力和等效时间求二阶导数，公式为

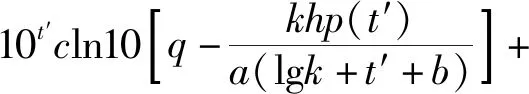
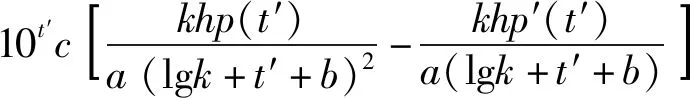
(10)

当此二阶导数为0时。压力对等效时间的一阶导数曲线存在极大值，压恢曲线出现拐点，此时存在关系式为

(11)

设m=lgk+t′+b，则可得到二项式

aqln10m2+(-khpln10-khp′)m+khp=0

(12)

根据求根公式可得m有两个根，分别为

t′→∞,m2→∞

(13)

图3展示了在压恢试井的半对数曲线及其一阶和二阶导数中此时刻的物理意义。

图3 压恢理论曲线及其一阶、二阶导数曲线图Fig.3 Pressure buildup test curve and its first and second derivative curves

2 试井资料解释方法改进

针对不同井储效应的气井，可以采取不同的拟合方法，基于井储效应对于气井试井的影响程度，将试井解释情况划分为两类，应用二阶导数的性质分别建立不同的试井解释模型，利用压恢曲线及其一阶、二阶导数曲线之间的耦合关系，对压恢曲线进行拟合，进而取得更准确的试井资料。

2.1 试井解释问题分类

2.1.1 第一类试井解释问题

对于大部分气井来说，由于储层埋深普遍较大，且气体压缩性强，压恢曲线很难达到近直线段。对于此类试井问题，需要综合运用二阶导数的零点以及一阶导数的极值点性质进行分析。

对于m1，由二阶导数公式进行分析。在该点处，考虑表皮因子的系数b和地层系数kh满足关系式

(14)

代入一阶导数公式得

(15)

由此可得地层系数kh、井储系数C以及考虑表皮因子的系数b之间的关系。对压力恢复值随等效时间的变化、压力恢复值随等效时间的一阶导数及二阶导数变化情况进行拟合，耦合多条曲线间参数值，从而得到较准确的试井解释参数。

2.1.2 第二类试井解释问题

针对井储效应不明显的气井，在压恢试井中曲线能够达到近直线段，则可对压恢曲线后期近直线段进行线性拟合，分析直线斜率，从而得到地层系数。

当t′→∞，m2为t′的同阶无穷大。

根据微分方程[式(9)]的数值解结果，此时井筒压力恢复值随时间的变化曲线近似为一条直线，二项式公式[式(12)]可写为

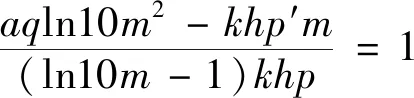
(16)

由微分方程数值解的结果可知，在压恢试井后期，压力对等效时间的二阶导数趋近于0，压力对等效时间的一阶导数为常数，对于式(16)由洛必达法则可得

(17)

由此可得地层系数参数，代入式(14)、式(15)中即可得到其他地层参数。

2.2 实际数据拟合方法改进

在试井作业时，需要经由压力计记录关井之后的压力变化曲线，一般每隔一个较短的时间记录一次数据。针对试井资料特点，采用有限差分法对试井中压力与等效时间的一阶导数和二阶导数的变化关系进行差分离散。

一阶差商：

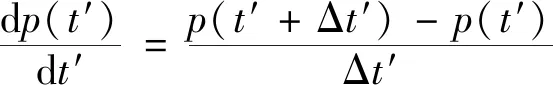
(18)

二阶差商：

(19)

从而得到实际试井资料中压力对时间的一阶导数值和二阶导数值随等效时间的变化。根据以上推论，在此连续的数值中，可以得出如下结果。

(1)当压力恢复对等效时间的一阶导数值达到最大值，则压恢曲线达到第一个拐点，由压恢试井分析模型，此时的压力恢复及其一阶导数值、井储系数C、地层系数kh、考虑表皮因子的系数b存在关系如式(15)所示。基于实际生产数据，通过调整参数拟合理论公式，即可得到井储系数、地层系数、表皮因子等参数。

(2)若生产井的井储效应较小，当压恢试井后期，压力恢复对等效时间的一阶导数值几乎不发生变化时，则压恢试井曲线表现为一条近乎直线的形态，且斜率满足关系式如式(17)所示，此时可针对压恢试井后期曲线直接进行线性拟合，得到地层系数，并回代入式(14)、式(15)中，从而得到各试井解释参数。

对压力恢复值随等效时间的变化、压力恢复值随等效时间的一阶导数变化情况及二阶导数变化情况进行耦合，能够更有效的拟合实际数据，从而提高试井解释的准确度。

3 实际试井资料拟合

A区块位于苏里格气田西区西北部，地质储量1 090.15×108m3，，投产井数243口，其中水平井38口，直井205口，主力产层为盒8段、山1段、山2段，2014年建产规模达6.0×108m3，2015年至今稳产规模达5.0×108m3。

X井为该区块2011年开发井，该井于2011年10月27日开钻，于2011年11月20日完钻，完钻井深3 622.0 m，完钻层位为马家沟组。其他流体及地层参数如表1所示。

表1 井、储层和流体性质参数表Table 1 Parameter tables of well,reservoir and fluid properties

2014年9月18日对该井进行压恢试井，试井前流量为2.2×104m3/d，首先进行通井，通完井后于9月23日关井进行压力恢复试井，11月7日压力恢复试井结束，压力恢复曲线如图4所示。

图4 压恢试井实测压力恢复图 Fig.4 Actual pressure recovery diagram of the pressure buildup test

在半对数坐标中，压力恢复值和等效时间之间的关系、压力恢复一阶导数值和等效时间的关系如图5所示。

由图5可以看到，在对该气井进行压恢作业时，天然气压缩性强，且气井较深，井筒储集效应明显，至压恢试井结束时，压恢曲线依然难以达到直线段，因此，将其归为第二类试井解释问题，需要结合导数曲线的第一个极大值点对试井资料进行解释。

图5 压恢试井实测资料半对数曲线图Fig.5 Semilogarithmic curve of measured data of actual pressure buildup test

根据试井资料，应用二阶导数法进行分析，可以认为当等效时间为2.85时，试井曲线的一阶导数值达到一个极大值为4.098，此时对应的恢复压力为6.6 MPa，根据式(13)，则可得到常数m和地层系数kh之间的关系。进而可通过计算机辅助手段，应用分析方程及数值解结果，耦合压力恢复值随等效时间的变化曲线、压力恢复值随等效时间的一阶导数变化曲线和二阶导数变化曲线，调整井储系数C、地层系数kh等值，对实际生产数据降噪处理后进行拟合，得到拟合结果如图6所示。

图6 压恢资料半对数曲线拟合效果图Fig.6 Semilogarithmic curve fitting effect diagram of the pressure buildup test data

根据压力随等效时间变化的泰勒展开，对压力的一阶导数拟合结果的截断误差为O(Δx)，对压力的二阶导数拟合结果的截断误差为O(Δx2)，运用有限差分方法，对压恢曲线的多阶导数曲线进行拟合，耦合多曲线拟合结果可以有效提高试井解释准确度，然而，阶数越高，截断误差越小，受工程和地质因素影响，实测数据难以达到满足高阶导数拟合要求的精度，即使经降噪处理后在拟合过程中仍不可避免地出现拟合结果差等问题，根据实践分析，耦合压恢曲线及其一阶、二阶导数曲线的拟合结果能够在减少数据拟合难度的情况下有效提高试井解释准确度。

运用试井模型对该试井曲线进行拟合，可以明显看到，相比常规试井模型，改进后的试井模型对于实际数据的拟合有着更好的精度，如图7所示。

图7 改进前和改进后试井模型拟合数据对比图Fig.7 Comparison of fitting data of well test model before and after improvement

试井资料实际值(根据后续生产资料得出)、常规模型预测值、改进模型预测值的对比如表2所示。

表2 不同方法预测地层系数表Table 2 Prediction of formation coefficient table by different methods

根据拟合得到的结果，常规模型因为没有考虑井储效应的影响，得到的地层系数值明显偏大，而改进后的模型得到的地层系数值接近实际值，从而使试井解释的准确度大幅度增加，根据改进后的模型，得到该井的井筒储集系数为8.53，表皮系数为2.2。

4 结论

(1)在常规试井理论基础上，通过数学推导，得到了考虑井储效应的气井试井新模型，明确了井储效应对压恢试井前期的半对数曲线的影响程度，井储效应越大，试井初期压力恢复速度越慢，在半对数曲线上表现为曲线凹度增大，压恢分析曲线的直线段出现时间越晚。

(2)系统分析了井储效应和表皮因子影响下的压力恢复值随等效时间变化的二阶导数模型，按照井储效应对气井试井曲线的影响程度大小，划分了两类试井解释问题，并结合二阶导数性质，分别推导了试井参数解释的理论模型，形成了考虑井储效应的气井解释的新方法。

(3)针对井储效应严重，压恢试井的半对数曲线很难达到直线段的情况，基于实际试井资料，应用理论模型，结合有限差分方法，在半对数坐标系中分别对压力恢复值及其多阶导数曲线进行拟合，实践表明应用二阶导数可以在减少数据拟合难度的情况下有效提高拟合精度。多条曲线的耦合结果有效提高了试井解释的准确度。