基于土水分特征曲线的废弃泥固化机理研究

吴言坤， 白 坤， 江苏洋， 杨志超， 袁 锐

（1.清华大学土木水利学院，北京 100084； 2.中铁十四局集团有限公司，济南 250014；3.中铁十四局集团大盾构工程有限公司，南京 211899； 4.河海大学土木与交通学院，南京 210098）

泥水盾构长距离穿越粉质黏土地层时会产生大量的废弃泥浆，常规处置手段如自然晾晒、外运，不仅容易产生二次污染，而且会占用大量宝贵的土地资源［1-2］. 通过向其中添加固化材料经过固化处理形成可以利用的土工材料，是废弃泥浆资源化利用的重要方向. 目前这方面的研究重点集中于固化材料的种类、配方，以及固化土的强度和变形等方面，关于废弃泥浆固化机理方面的研究也局限于从生成物或微观结构的角度定性地进行评价，从定量化的角度对废弃泥浆的固化机理进行研究尚不多见［3-5］.

废弃泥浆固化机理是废弃泥浆中的水分和固化材料发生一系列复杂的物理化学反应而改变了其初始的存在形式［6-8］，使固化土的物理力学性质发生了本质的变化. 分析固化过程中水分转化规律是研究废弃泥浆固化机理一条新途径［9-12］. 废弃泥固化后其中的绝大部分水从原来的重力水和自由水转化为三部分：结合水、吸着水和毛细水. 毛细水和吸着水是形成土中负压的主要因素，通过测量固化过程中吸力的变化建立相应的水分模型将吸着水和毛细水分开，并考虑蒸发因素可以实现对固化过程中形成的结合水、吸着水和毛细水的定量化研究.

废弃泥固化过程中吸力的测量和一般土吸力的测量有所不同，首先废弃泥在固化过程当中吸力不断地在发生变化，要保证吸力能够连续、准确测量；其次固化的过程是一个不可逆的过程，如果采用类似压力板测量的方法重新将试样饱和再进行排水，就难以准确模拟固化过程中水分和吸力的变化；为了在固化过程中准确、实时地记录吸力的变化，可以采用对吸力变化反应迅速的张力计进行测定. 但是张力计的测量范围相当有限（0～90 kPa），所以需要通过其他途径获取其高吸力段的数据.

研究表明土体结构（颗粒粒径、表面积、体积、孔隙大小等）具有自相似特征，即具有一定的分形维数［13-14］.Childs［15］在第一届国际土壤学会议上第一次提出土体水分特征曲线的概念，水分特征曲线是土结构分布的反映，根据所确定的反映土体结构特征分形维数进而可推导出具有一定物理意义的土体水力特性的分形描述模型.

1 废弃泥固化土分形维数研究

1.1 废弃泥固化土试样的制备

试验所选用的废弃泥取自济南市济泺路穿黄隧道工程现场废弃泥浆沉淀池的底部泥浆，其基本物理力学性质指标见表1.

表1 废弃泥物理力学性质指标Tab.1 The physical and mechanical properties of dredged sludge

本试验选择水泥、粉煤灰及石膏等固化材料进行复合添加，1 m3废弃泥中添加50 kg水泥、100 kg粉煤灰和15 kg石膏，之后将废弃泥和固化材料以100 r/min的机械方式强制搅拌充分，共制样2组.

1.2 水分特征曲线分形维数的确定

Tyler 和Wheatcraft［16］认为：假定具有自相似结构的多孔介质由大小不同的颗粒组成，各级土粒的比重ρi=ρ，则大于某一特征平均粒径Rˉi的质量为：

式中：D为描述自相似性的分形维数；Cv、λv为常数，与颗粒大小、形状有关.

当假定平均粒径Rˉi=0 时，式（1）即为计算全部土体颗粒的总质量MT. 假定Rmax为最大的土颗粒尺寸，D粒径为颗粒大小分布的分形维数，可以推导出

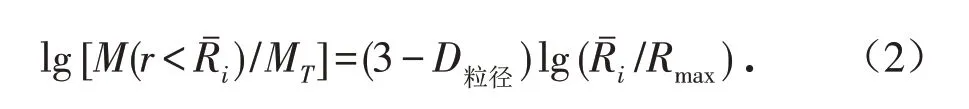
黄冠华和詹卫华［17］的研究表明水分特性曲线的分形维数与基于质量颗粒大小分布的分形维数两者基本接近且呈线性关系

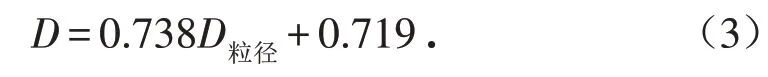
采用比重计法测得的废弃泥固化土粒径分布曲线如图1所示.

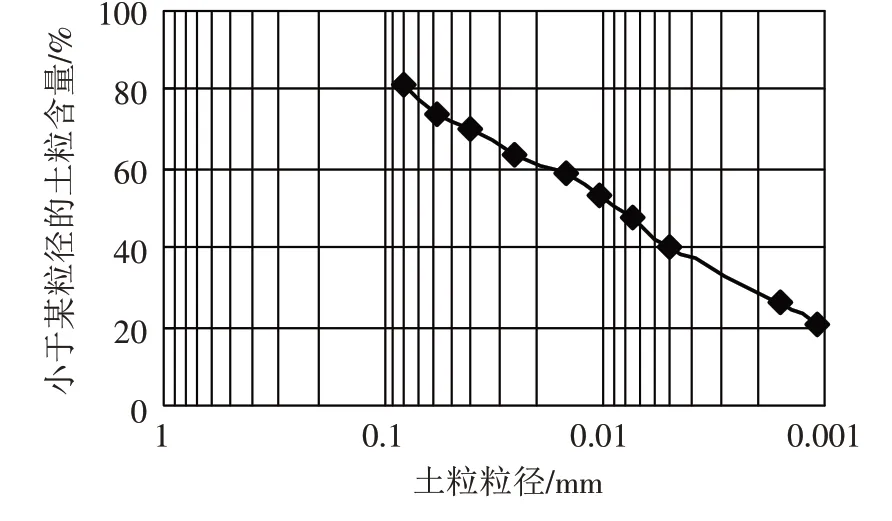
图1 废弃泥固化土颗分曲线Fig.1 Grain-size distribution curve of solidified dredge sludge

根据式（2）对颗分试验的结果进行整理，并根据最小二乘法拟合上述数据，拟合的土粒分布方程具有很好的线性相关性（图2）. 结合图2 及式（2），可以获得颗粒大小分布分形维数D粒径=2.623，根据式（3）计算得到水分特征分形维数D=2.654 8.

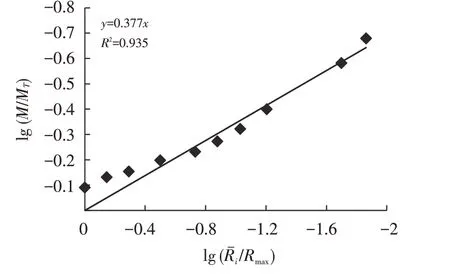
图2 废弃泥固化土质量分形模型Fig.2 Quality fractal model of solidified dredge sludge

2 废弃泥固化土水分特征曲线的分形模型

2.1 水分特征曲线的分形描述

Pfeifer 和Avnir［18］认为，在三维测度空间内多孔介质的孔隙分布分形模型的积分形式可以表述为：

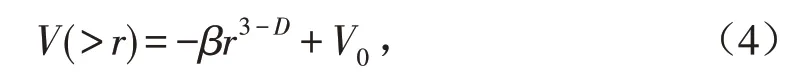
式中：V(>r)是尺寸大于一给定值r的累计孔隙体积；D是孔隙尺寸分布的分维数；β为常数；V0为积分常数.

土体孔隙率

式中：θ是土体的体积含水率；VT是土样的总体积.

式（4）中的积分常数V0为半径介于最小孔隙尺寸0和最大孔隙尺寸rmax之间的孔隙体积，

当土体饱和时有θs=n，其中，θs是土体饱和体积含水率，即土体中所有孔隙充满水时，水的体积与整个土体体积比值. 将式（4）、（6）以及Young-Laplace方程代入（5）式可以得到

式中：ψa为进气值；D为反映土体水力特征的分形维数；θ和ψ分别为实测的土体不同体积含水率和基质吸力；θs≤V0/VT≤1，当V0/VT=θs时，上式转化成与Campbell 定律一样的形式；当V0/VT=1 时，上式的结果与Rieu和Sposito研究的成果具有一致的形式.

对于相同的土样和一定型号的张力计V0/VT，θs以及ψa可以近似假定为常数，令ζ=θs-V0/VT，η=V0/VT，则式（7）可以变为

式中：ζ、η为常数，可以通过最小二乘法得到. 式（8）即为非饱和土水分特征曲线分形模型.

2.2 废弃泥固化过程中基质吸力的测量及参数拟合

试验中基质吸力的测量采用Daiki-3150型张力计，观测连续进行了4 d直至超出了张力计的测量范围.两组试验数据见图3，根据试样的含水率和吸力通过最小二乘法拟合的ζ、η值，见图4.

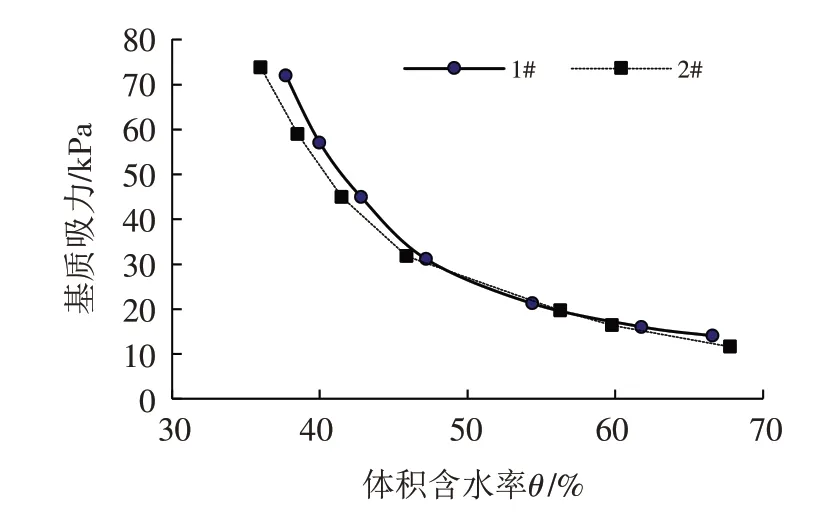
图3 实测水分特征曲线Fig.3 Measured water characteristic curves

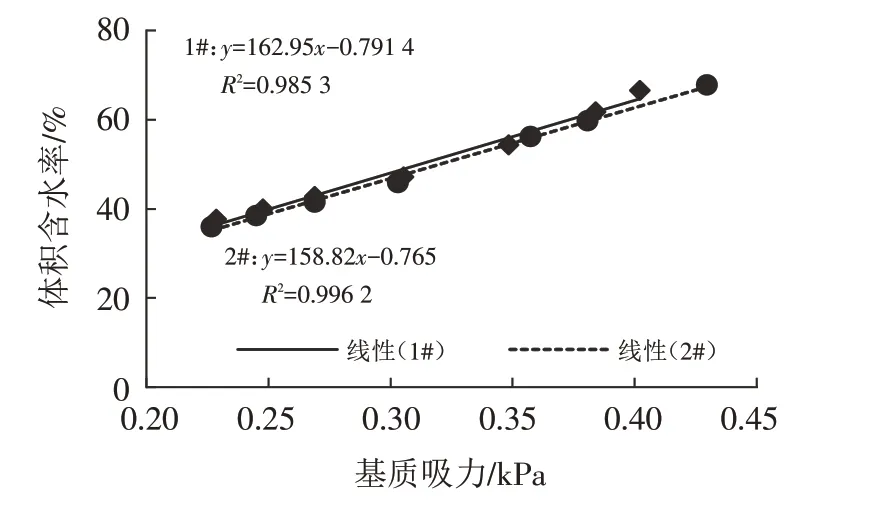
图4 模型参数拟合曲线Fig.4 Fitted curves of model parameters

根据拟合的参数ζ、η即可得到废弃泥固化过程完整的水分特征曲线（见图5）.

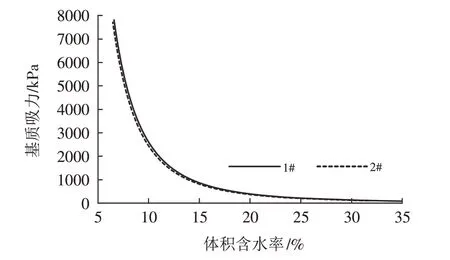
图5 废弃泥固化土水分特征曲线Fig.5 Water characteristic curves of solidified dredge sludge

3 废弃泥固化机理研究

土体中的基质吸力由毛细水吸力和土体表面吸着水吸力两部分组成，毛细水和土颗粒结合能较弱，具有较低的水分势能，即毛细水占优势时的基质吸力较小；吸着水和土颗粒结合能较强具有较高的水分势能，即吸附水占优势时基质吸力较大. 随着土体含水量的变化，基质吸力发生变化，基质吸力的两个组成部分在总基质吸力中所占的比例也在发生变化. 土体含水量与基质吸力的关系曲线实质上是反映这两种作用的共同效应. 为了在含水量与基质吸力的关系曲线上反映出基质吸力两个组成部分的变化，文献［19］建立的含水量与基质吸力之间相关关系数学模型为：

式中：ω为土体质量含水量；a，b，c，d为统计参数.

采用式（9）将图5的土水分特征曲线重新进行拟合，并分别将ω1=aψ-b和ω2=cψ-d绘制于图6中.

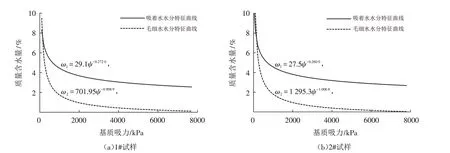
图6 吸着水和毛细水水分特征Fig.6 Water characteristics of capillary water and absorbing water

综合图5和图6可以看出，式（9）可以反映出毛细水和吸着水随基质吸力变化而改变的规律：①在固化过程中含水量在逐渐降低，吸力在不断增加，在高吸力段毛细水的含量很小，固化土以吸着水为主；②在低吸力段毛细水的含量随基质吸力的减小而急剧增大，吸着水的含量虽然也在增加，但是增加的幅度小于毛细水增加的速度；③随着固化的进行土的骨架结构越来越致密，所以毛细水下降得相当迅速，形成的固化体具有较强的吸附作用导致吸着水量下降较为缓慢，而且到高吸力阶段吸着水水量依然较高；④去除水分蒸发量之后毛细水和吸着水减少的量，即为和固化材料发生水化反应生成结合水的量.

假定忽略不计能够测得基质吸力前发生水化反应的水量，则固化过程中的吸着水、毛细水累计减少量分别可以表示为：

其中：ψ0为实测的吸力初始值；ms为固化土颗粒质量.

假定蒸发的水量全部来自毛细水和吸着水的减少量，则与固化材料发生反应形成的结合水水量为：

关于蒸发量的计算可以采用Gardner［20］提出的土壤干燥模型：蒸发累积值E与蒸发历时t的平方根呈线性关系

根据文献［21］的研究结果，水分扩散率和分形维数成如下关系

综合式（13）～（15）可得不同基质吸力条件下的土体累计蒸发量计算模型.

根据上述的数学模型和分析，本文计算了1 m3的废弃泥在固化过程中毛细水、吸着水、蒸发水以及结合水的变化量，如图7所示.

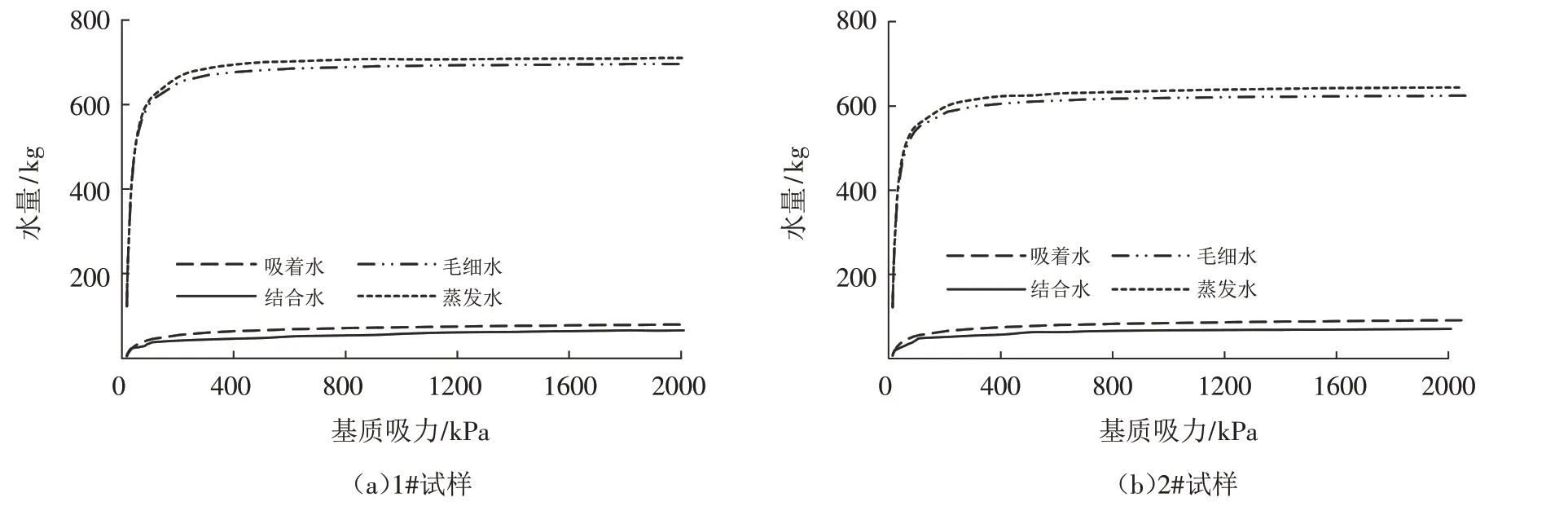
图7 吸着水、毛细水、蒸发水、结合水水量变化关系曲线Fig.7 Relationship among water variations of the absorbing water，capillary water，evaporated water and combined water

从图7中可以看出：①在固化进行的早期吸着水、毛细水、蒸发水以及结合水水量的变化都是很快的，而到了后期其水分变化趋于平缓，说明大部分固化反应都是在固化早期完成的，主要是因为形成的水合物包裹于固化材料的表面阻碍了水化反应的进一步进行；②上述四种水分变化曲线都存在明显的拐点，结合水增长量的拐点和吸着水减少量的拐点以及变化趋势较为一致，说明吸着水是结合水的主要来源，而蒸发水和毛细水的拐点以及变化趋势较为一致，说明毛细水是蒸发水的主要来源，这和实际情况中水化反应中优先反应颗粒表层水以及蒸发优先蒸发结合势能较低的水是一致的；③由于假定忽略不计吸力测量之前结合水的生成量，所以按照本文模型计算的结合水生成量偏低.

4 结论

1）采用张力计测定废弃泥在固化过程中基质吸力的变化是可行的，能够实时地反映固化过程中基质吸力和含水量的变化；

2）通过废弃泥固化土的水力分形维数和张力计测得的低吸力状态的吸力值可以建立其水分特征曲线的分形模型，通过模型能够获得完整的水分特征曲线以弥补张力计在量程方面的不足；

3）通过所建立的数学模型将毛细水和吸着水分离，并将毛细水和吸着水水量进行量化，为进一步揭示固化机理奠定基础；

4）考虑蒸发模型后能够量化固化反应过程中结合水的生成量，揭示了毛细水、吸着水、蒸发水以及结合水之间的关系，从定量和定性的角度阐明了结合水的水量以及来源，为固化材料的配方以及固化土力学性质的研究提供了基础资料；

5）为了能够更准确深入地研究固化过程中水分特征曲线的形式，应当采用水分离心机测定高吸力状态的吸力值，应用干燥加速度试验对水分势能进行更准确地量化，以修正所建立的分离毛细水和吸着水的数学模型.