碎石土边坡坡度对桩基地震响应的影响

甘 俊， 谭维佳， 岳 宏， 祝铠甲， 马长政

（1.青海煤炭地质勘查院，西宁 810000； 2.长安大学地质工程与测绘学院，西安 710054）

桩基础因具有适应性强，承载力高等优点，特别适用于山区斜坡地形的施工条件. 实际上，西南山区斜坡工程90%以上为桩基础. 但该区受到印度板块和欧亚板块的碰撞影响，经常发生强烈地震，汶川8.0级和芦山7.0级地震中，地震致地基基础损坏达到30%～40%.

桩的地震动力响应主要是指地震荷载作用下桩土相互作用体系中结构变形特性和受力特征［1］. 一直以来，国内外学者对于承受水平作用的桩基础研究较少，往往偏重于竖向作用下桩-土工作特性的研究［2］. 研究主要集中在动力方程的求解、动力响应试验、动力特性参数等方面，对悬臂抗滑桩加固边坡地震动力响应［3］、可液化地基上边坡加固桩地震动力破坏特点［4］、锚杆抗滑桩加固边坡工程动力稳定性［5］、地震荷载下顺层岩体边坡响应特性和抗滑桩控制效果［6］、下伏基岩堆积体边坡抗滑桩加固前后地震响应［7］等方面开展了模式试验研究，由于模型试验成本高、尺寸小，模型桩的动力试验不能有效地表达实际的桩-土相互作用，至今得到有价值的试验结果非常有限. 随后有学者基于OpenSees［8］、Quasi-3D FEM［9］、PILE3D［10］、ABAQUS［11］、FLAC3D等［12］数值平台进一步考虑了土的材料和几何非线性模拟桩-土相互作用. 为了研究地震作用下倾斜场地桩-土-结构的相互作用规律，张卢明等［13］采用分离相似设计方法和基于连续介质力学的离散元法，进行了群桩结构模型振动台试验与数值分析，获得了身动应力变化规律及处置场的整体稳定性. 李见飞等［14］提出一种基于Newmark滑块原理的抗滑桩加固三维平台土坡地震位移方法，并以抗滑桩加固的三维平台边坡作为研究对象，基于极限分析上限定理分析了三维平台边坡的地震稳定性［15］. 同时，考虑了地震-降雨耦合作用［16］、抗滑桩排布方式［17］、桩间距［18］等因素对加固边坡安全性的影响. 但是上述研究均忽略边坡坡度这一重要边坡几何参数对斜坡建筑桩基地震响应的影响，特别是对于碎石土边坡，至今仍未明确不同坡度桩-土体系受地震荷载时的变形效应，以至于斜坡桩基设计仅依据长期的实践经验进行设计，缺乏理论支撑.

本文以西南地区穿越典型地形地貌和地基土大类的某一线路工程为例，采用PLAXIS3D有限元软件建立边坡桩-土体系分析模型，详细分析边坡坡度对斜坡桩基地震响应的影响.

1 工程概况

该输电线路工程位于龙门山中、高山区与四川盆地北缘弧形褶缓低山丘陵过渡地带，属于Ⅷ度地震烈度区，穿越地形坡度为30°（如图1所示）. 场地下覆第三系砂岩，呈层状，产状为245°∠23°，节理发育. 第四系覆盖层为第四系坡残积物（Q4el+dl），残坡积碎石土，分布在斜坡的表层，粒径一般为3～8 cm，中等粒径也可达到20 cm，棱角状，磨圆度差，块石之间充填少量黏性土，厚3～5 m.

图1 线路工程所穿越的斜坡全貌Fig.1 The slope of the transmission line project in this study

该线路工程所用基础为混凝土人工挖孔桩基础. 桩径1.0 m，桩长8 m，出露0.6 m. 混凝土等级C25.

2 分析模型建立

根据场地、地基条件以及桩基础设计方案，并以勘察钻孔ZL01～ZL08的8口钻孔揭露地层为依托采用PLAXIS3D建立计算模型，该模型的宽450 m（Y）、长700 m（X）、高200 m，所建立的模型见图2所示. 底部边界约束位移，顶部边界为自由边界；侧向边界设定水平向为位移约束；地震力作用时模型周围边界选取自由场边界，主体网格的侧边界通过阻尼器与自由场网格进行耦合，自由场网格的不平衡力施加到主体网格的边界上.

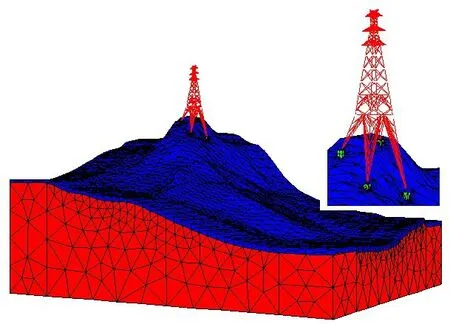
图2 计算模型Fig.2 The computational model

建模过程中，岩土体采用四面体、五面体和六面体混合网格单元相互匹配、连接组成. 桩基础实际尺寸采用柱型网格（即六面体网格）进行建模. 通过网格节点连接上部结构和桩周土体，上部结构采用空间梁单元模拟［19］. 计算中岩土体物理力学参数见表1所示.

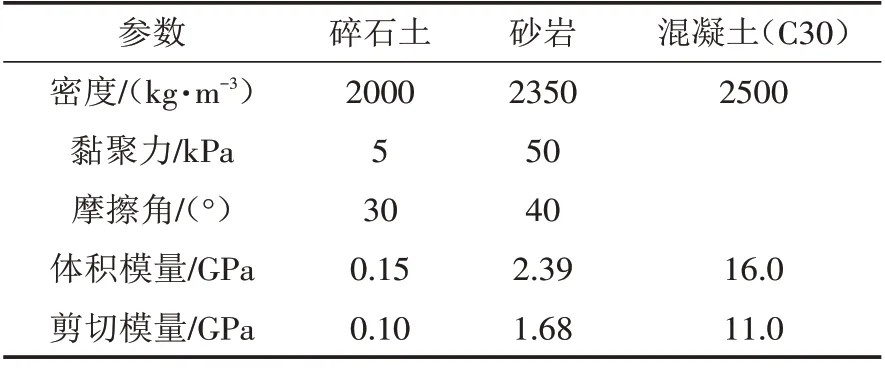
表1 物理力学参数表Tab.1 Physical and mechanical parameters

为了分析边坡坡度对桩基础地震响应的影响，坡度考虑为0°、15°、30°、45°.

2）本文动力计算中材料阻尼的设定采用瑞雷阻尼，可表示成质量矩阵M和刚度矩阵K的线性组合：

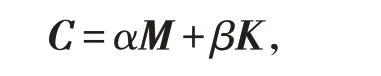
式中α、β为瑞雷阻尼系数，

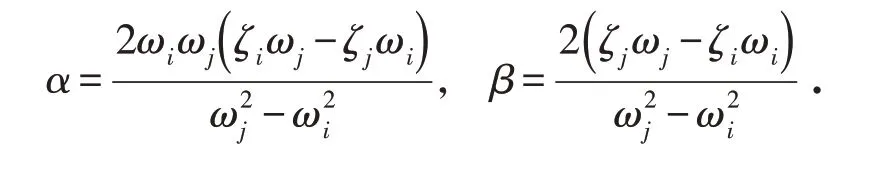
其中：ωi、ωj分别为结构的第i和第j振型的固有频率；ζi、ζj为相应的阻尼比. 一般情况下i、j分别取1和2［20］.

3）地震荷载选取芦山地震名山科技强震动台数据，仅考虑水平地震作用. 通过SeismoSignal进行人工滤波，处理后地震作用历时30 s，单位时间步长0.005 s，历时8～18 s为振动峰值区，地震主震频率为10 Hz. 波形图如图3所示. 计算时，将加速度时程从基底输入，相当于施加于研究对象所有单元上，从相对运动角度来看，认为对象不动而基岩作反向运动.

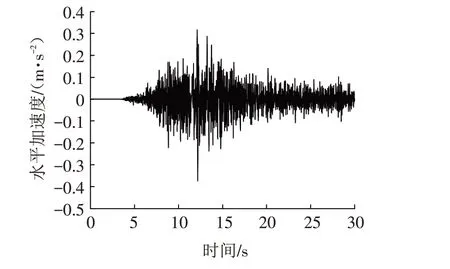
图3 地震加速度时程曲线Fig.3 Time history curve of seismic acceleration

3 对桩基响应表征参数的影响

桩基础动力表征参数主要包括桩基础的加速度、内力和位移的变化.

3.1 对桩身加速度

在桩身中心沿深度方向每隔一定距离布设一个考查点，收集沿地震传播方向的水平向峰值加速度. 由图4 可见，水平场地中基底加速度与输入地震波幅值大致相同；桩基自下而上加速度变化不明显，桩顶靠近地面处的加速度也并未出现明显的放大效应. 说明，密实碎石土水平场地对桩基础地震加速度反应并不明显. 斜坡场地（>0°坡），桩身各处表现出相对基底的加速度放大效应. 说明随着斜坡坡度的增大，桩-土运动相互作用已逐渐凸显. 同时，桩底峰值加速度均近似相同，也说明下伏土层对桩具有显著的嵌固作用.

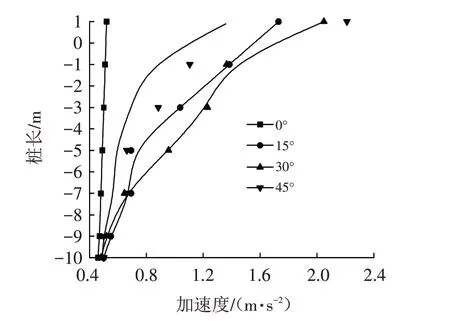
图4 不同坡度桩身加速度-埋深关系曲线Fig.4 Acceleration-buried depth relationship curves of piles with different slope gradients

桩身加速度随桩身从桩底到桩顶成非线性变化，在桩顶最大，桩底最小，除0°坡外，其他坡度场地桩基桩顶加速度为1.5～2.0 m/s2，比原始地震输入放大了3～4 倍. 桩顶加速度最大值随斜坡坡度正切值关系近似为αmax=27-97×tanβ+126×（tanβ）2关系，见图5.

图5 桩身加速度最大值-坡度关系曲线Fig.5 Relationship curve between pile maximum acceleration and slope gradient

3.2 对桩身弯矩

收集垂直坡向的桩身两侧面的应力，应力收集时取桩侧面中线点、两边缘线不同深度的应力，计算其平均值，再根据桩身两侧面的应力差计算桩所受的弯矩. 从图6可见，桩身弯矩从桩底到桩顶先增后减，桩顶至3～3.5 倍桩径范围增大，随后开始减小，至桩底为最小值，说明在桩顶遭受水平地震荷载时，桩身下部并不会受到明显的影响. 因为桩下部反应主要由土层控制，而上部土层由于斜坡坡度的存在对桩的嵌固作用效果不佳；另一方面说明了由于斜坡坡度的影响，一定深度上、下土层差异性逐渐加大，斜坡土体失效与未失效处桩产生了明显的弯矩突变，该处较其他位置弯矩绝对值要大很多.

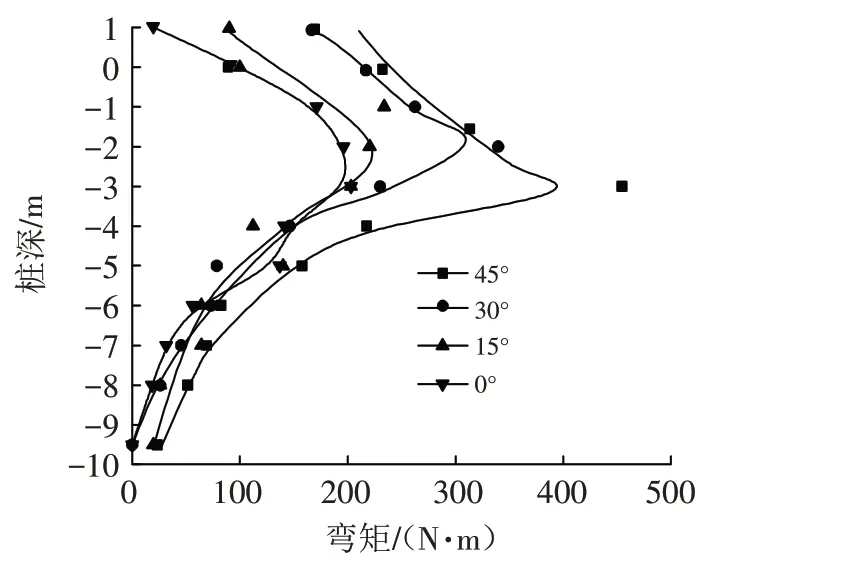
图6 不同坡度桩身弯矩-埋深曲线Fig.6 Bending moment-buried depth curves of piles with different slope gradients

斜坡坡度从0°～45°，桩身最大弯矩从150 N·m 增大到400 N·m，桩的弯矩随坡度增加响应强烈. 桩身弯矩包络最大值随斜坡坡度正切值关系亦近似线性变形. 趋势线公式为M=187+262×tanβ，如图7所示.

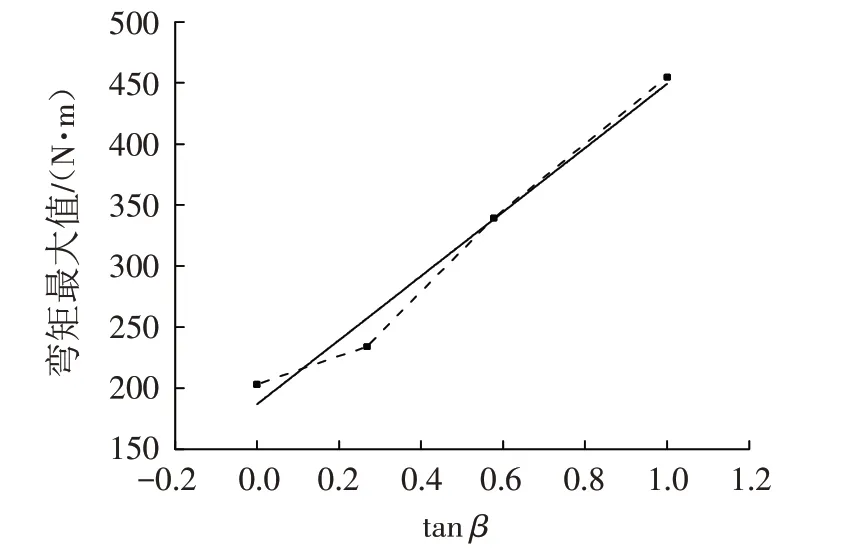
图7 桩身弯矩最大值-坡度关系曲线Fig.7 Relationship curve between pile maximum bending moment and slope gradient

3.3 对桩身位移的影响

与加速度考查点设置相同，位移分别收集不同地震历时时刻的水平向位移. 从图8可见，随斜坡坡度的增加，桩各深度的位移幅值逐渐增大，尤其是在桩身中上部（约0.5倍桩身至桩顶），桩身位移随斜坡坡度的增大而迅速增大. 斜坡坡度较缓时（0°～15°），坡度每增加15°，桩顶最大位移增加约5 mm；斜坡坡度超过15°，坡度每增加15°，桩顶最大位移增加约15 mm.

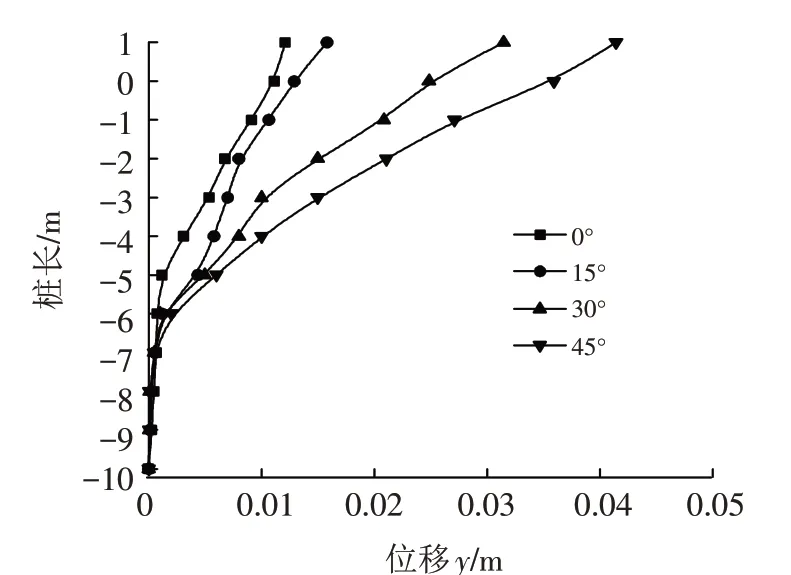
图8 不同坡度桩身位移-埋深曲线Fig.8 Displacement-buried depth curves of piles with different slope gradients

图9 为桩顶最大位移与斜坡坡度正切值之间的关系，从图中可见，桩顶最大位移与斜坡坡度正切值随着斜坡坡度的增大近似呈线性关系，趋势线为y=0.01×tanβ+0.01.

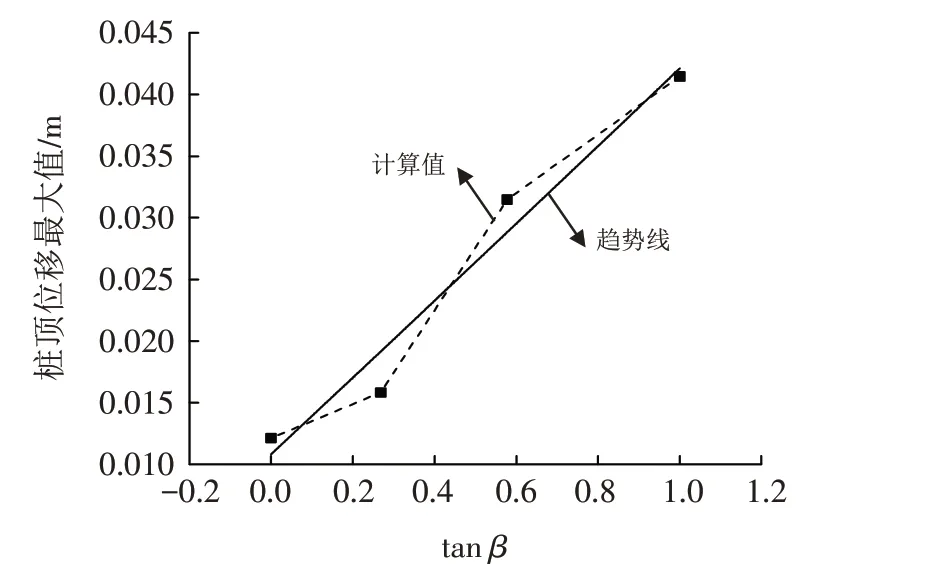
图9 桩顶位移最大值-坡度关系曲线Fig.9 Relationship curve between pile maximum displacement and slope gradient

4 对桩-土动力p-y曲线的影响

图10为基准模型不同桩深桩-土体系动力p-y曲线图. 动荷载作用下土的应力-应变关系具有明显的非线性. 从荷载作用全过程的滞回曲线中选取所经过的极值点或拐点作为该滞回圈的顶点，并假定此点为骨架线上的点.

从图10中可见，碎石土动力p-y骨干曲线的形状为上“凸”型. 从振动初期至振动结束过程中p和y从成正比例变化逐渐呈现步调不一致，尤其对于浅表层土体，两者不一致性表现得甚为明显，这一现象说明斜坡场地桩身上部土体易出现大变形而丧失抵抗强度；另外，p-y曲线随着埋深的增加，土体刚度（kini）逐渐变大，土反力（pu）增大，滞回圈面积（S）却在减小，说明桩-土相互作用动力耗能作用随深度增加而逐渐增大，但滞回圈形式近似相似.

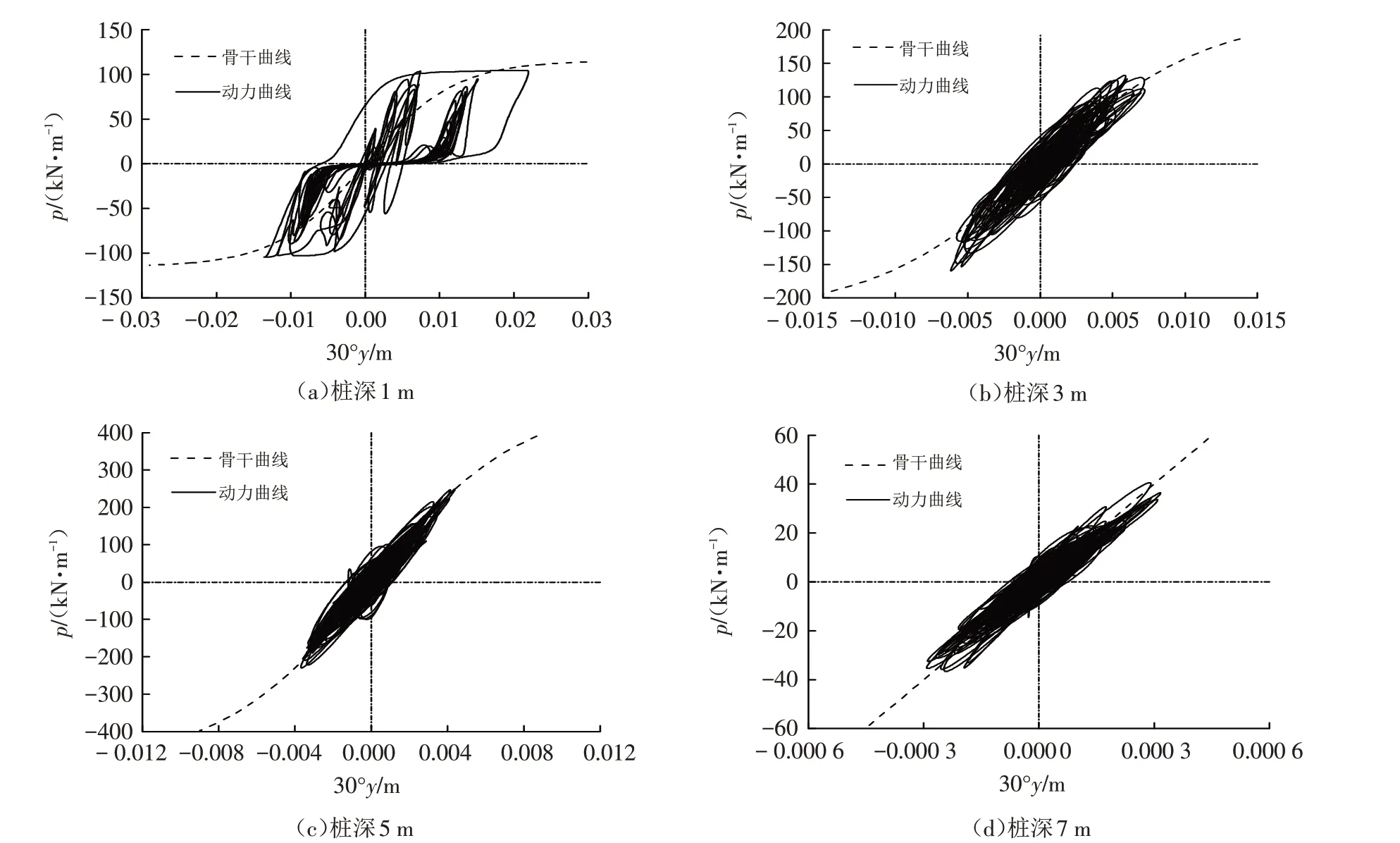
图10 不同桩深桩-土体系动力p-y曲线Fig.10 Dynamic p-y curves of pile-soil system with different pile depths

进一步整理不同坡度下，桩-土体系动力p-y骨干曲线斜率（kini）、极限土抗力（pu）及滞回圈面积（S）随深度（z）、坡度（β）的变化情况见图11所示. 其中图11a，b，c分别为logkini-log（zcosβ），pu-zcosβ，S-log（zcosβ）的关系曲线. 其中滞回圈面积按椭圆形面积计算（S=πab，其中a为滞回圈长轴长度；b为滞回圈短轴长度）.

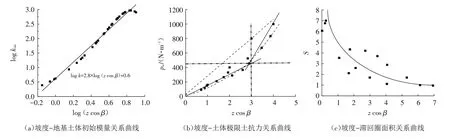
图11 动力p-y曲线各参量-斜坡坡度关系Fig.11 Relationship between various parameters of dynamic p-y curve and slope gradient

由图11a 可知，地基土体初始模量随着zcosβ的增加而增大，整体趋势为线性增大，曲线大致分为两个阶段：①log（zcosβ）≤0.8，正比增大段；②log（zcosβ）>0.8，稳定变化段. 桩埋深越深，振动过程对其影响越小，即，桩埋深超过8倍桩径深度，如若该深度桩周土体处于弹性状态时，外界荷载对该深度以下桩基础变形影响不明显.

图11 b为地基极限土抗力随坡度、zcosβ的关系曲线. 地基极限土抗力随着zcosβ的增加而增大，整体趋势为线性增大. 其趋势分布大致分为两个线性变化段：zcosβ≤3和zcosβ>3，后一段曲线斜率明显大于前一段；该深度与桩基础包络弯矩最大值出现位置近似相同，即可说明地基极限土体抗力与桩身变形密切相关.

图11c为滞回圈面积随坡度、深度（zcosβ）的关系曲线，两者关系相对离散，但总体来说近似双曲线变化.

5 结论

本文针对斜坡桩基抗震设计优化措施缺乏理论和实践支撑这一问题，以西南地区穿越典型地形地貌和地基土大类的某一线路工程为例，采用PLAXIS3D有限元软件建立边坡-桩-土体系分析模型，分析边坡坡度对桩身动力响应及动力p-y曲线的影响，研究结果如下：

1）斜坡场地桩基地震响应表征参数中桩基础的加速度、内力、位移受地震荷载影响明显，但由于斜坡坡度的影响，一定深度上、下土层差异性逐渐加大，斜坡上部土体丧失了抵抗强度使桩产生了明显的响应突变.

2）桩身加速度、弯矩、位移均随斜坡坡度增大而增大，但变化的幅度随桩深的增加越来越弱. 三者与坡度关系近似为：αmax=27-97×（tanβ）+126×（tanβ）2，M=187+262×（tanβ），y=0.01×tanβ+0.01.

3）地震输入下非线性碎石土动力p-y曲线相对来说较为规则且对称，随着埋深的增加，土体刚度逐渐变大，土反力增大，滞回圈面积减小.

4）桩-土体系动力p-y骨干曲线斜率（kini）、极限土抗力（pu）及滞回圈面积（S）随深度（z）、坡度（β）均呈一定的线性关系.