面向大规模交互数据空间划分的Voronoi图生成算法及应用 *
熊鹏文,周晓芸,熊宏锦,张婷婷
(1. 南昌大学 信息工程学院, 江西 南昌 330031; 2. 海装驻武汉地区军事代表局, 湖北 武汉 333000;3. 陆军工程大学 指挥控制工程学院, 江苏 南京 210007 )
Shamos和Hoey于1975年在“最近问题”中提出了Voronoi 图这一概念,从此拉开了计算几何的帷幕[1]。传统的Voronoi图是由连接任意两邻点直线的中垂线连接构成的[2]。平面中的点到最近的Voronoi单元都比其他的点到该Voronoi单元的距离要近。传统Voronoi图研究的是单个点对单个点的空间关系,它将每个点都视为是相互独立的。然而,在现实世界中,一个物体通常都处于和其他物体相互关联的状态中,我们不能仅仅把目光投向局部某个点,而应该从整体的角度去看待点与点之间的联系。
因此,针对多核心Voronoi图的研究受到了广大研究人员的关注,并取得了一些成果。但是由于Voronoi单元核心的数量限制,或者点集数量的限制,抑或是计算方式的限制,多核心Voronoi图都不能快速地对大规模数据进行空间划分。Barequet等[3]提出了两点核心Voronoi图,但是Voronoi单元核心的数量限制导致该算法的应用具有局限性;Chen等[4]提出的聚类诱导 Voronoi 图(Clustering Induced Voronoi Diagram,CIVD),虽考虑了点与点之间的影响函数关系,但是由于算法过于烦琐,只能生成小规模数据的Voronoi图,因此效率较低、普适性较差。陈学森等[5]提出的基于集合影响力的Voronoi算法,虽然对Voronoi单元核心数量受到限制的问题进行了处理,但是需要人为输入参数来调整Voronoi图划分的密度,实际处理起来较为复杂。卢嘉豪等[6]提出了平面相交多边形的Voronoi图,但是由于计算方式限制只能对少量目标进行Voronoi图生成。万静等[7]提出了障碍空间中基于Voronoi图的不确定数据聚类算法,但只考虑2级生成点以内的不确定数据和障碍情况,适用范围窄。
对此,为了更深入地研究点集在空间的分布关系,本文将Voronoi图的概念推广到基于密度的聚类算法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)的Voronoi图(Voronoi Diagram for DBSCAN,DBSCAN-VD),不再将二维平面中的点集视作相互独立的,而是通过聚类将点划分成一个一个的点集,从而研究点集与点集之间的联系。本文还提出一种自适应确定DBSCAN参数的算法,无须人为确定参数,通过利用数据集自身分布特性生成候选和参数[8],自动寻找聚类结果的簇数变化稳定区间,并将该区间中密度阈值最少时所对应的和参数作为最优参数。DBSCAN参数的自动选取不仅可以节省计算参数的时间,而且可以有效提高聚类的准确效果。最后以显微镜下嗜中性粒细胞的图像和我国地表火点分布图作为仿真实例,验证DBSCAN-VD算法解决大规模数据下空间划分问题的有效性。
1 DBSCAN聚类原理
DBSCAN聚类算法是一种基于密度的聚类算法,它可以在带有噪声的空间数据库中发现任意形状的聚类。DBSCAN聚类算法具有良好的抗噪能力。关于DBSCAN聚类算法的定义[9]如下:
定义1Reps邻域。假设存在空间中的点集D,∀p∈D,以对象p为中心、以给定半径Reps为半径的邻域称为对象p的Reps邻域。
定义2密度阈值Tminpts。假设存在空间中的点集D,∀p∈D,称满足对象p成为核心点的值为密度阈值Tminpts。
定义3核心点。 假设存在空间中的点集D,∀p∈D,∀{p1,p2,…,pn}∈D,p1,p2,…,pn在对象p的Reps邻域内,若Reps内点数大于Tminpts,表示对象p的Reps邻域内对象个数大于密度阈值,则定义p为核心点。
定义4边界点。假设存在空间中的点集D,∀p∈D,∀{p1,p2,…,pn}∈D,若Reps邻域内点的数量小于Tminpts,且落在核心点的邻域内,则称以上定义点为边界点。
定义5噪声点。假设存在空间中的点集D,∀p∈D,既不是核心点也不是边界点,则称p为噪声点。
DBSCAN算法的流程首先是将所有点标记为核心点、边界点或噪声点[10]。DBSCAN聚类演示如图1所示,A点为核心对象,以A点为圆心的Reps邻域内找到其他点。然后以各自的点为圆心、Reps为半径作圆,直到邻域内任意一个点在以Reps为半径作圆时,Reps邻域不能囊括其他点,则该点称之为边界点B、C。N点不能被任何以核心点为圆心、Reps为半径的圆包裹进去,所以称之为离群点。图中黑色箭头的指向表示密度可达,以A点为圆心、Reps为半径的圆构成的集合中包含了所有的密度直达样本,集合外的均不能密度直达,在这些密度可达的样本序列的Reps邻域内,所有的样本相互都是密度相连的[11]。

图1 DBSCAN聚类演示Fig.1 DBSCAN clustering demonstration
2 基于自适应DBSCAN聚类的Voronoi图的定义
2.1 传统Voronoi图的定义
Voronoi图是对空间的最邻近划分[12],在给定一些目标的情况下,将空间划分成若干个区域,所有划分区域内的任意一点都距离该区域内的目标最近。传统Voronoi图是根据平面点集绘制的分割图像,是针对每一个点与其他点之间的位置关系进行邻域划分。图2所示的是一个点集数量为8的Voronoi图,这8个点为Voronoi图的核心点,平面空间被任意两点连线的中垂线划分成若干个区域,这些区域为Voronoi单元,每个Voronoi单元中的任意一点都距离该Voronoi单元中的核心点最近。

图2 传统点集Voronoi图Fig.2 Voronoi diagram of traditional point set
令P={p1,p2,…,pn}为平面上n个点的集合,其中pi表示集合中的任意一点,d(p,q)表示点p与点q之间的欧式距离,则定义:
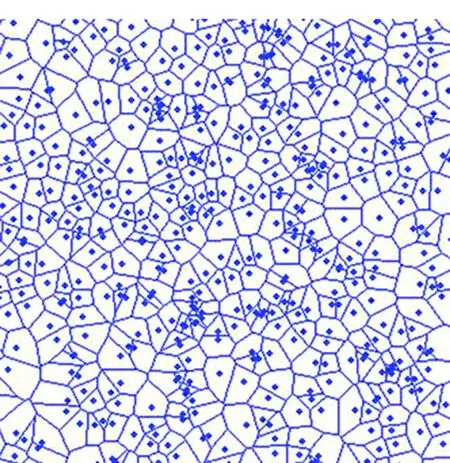
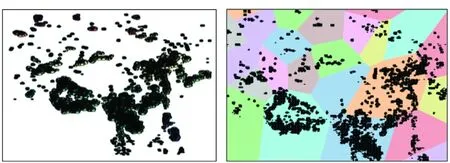
V(pi)={x|d(x,pi) 集合V(p)={V(p1),V(p2),…,V(pn)}便是Voronoi图[13]。 Voronoi图给出了平面的空间划分,集合中的元素为Voronoi核心点,如图2中的8个点。V(pi)是一个域,为对应于pi的Voronoi域,也称作Voronoi单元。划分平面空间的线段,即Voronoi单元的边界,为Voronoi边。 传统Voronoi图是针对每一个点进行Voronoi单元划分,Voronoi单元的数量随着点集的数量增加而增加。在点集数量过大的情况下,Voronoi图划分会产生图像分割过于密集、Voronoi单元格过多的问题。如图3所示的点集为500的Voronoi图,由于目标数量较多,对每一个点进行Voronoi分割产生的划分结果过于细致,实际应用价值很小。 图3 500个点的Voronoi图Fig.3 Voronoi diagram of 500 points 因此,由问题出发引出基于自适应DBSCAN聚类的Voronoi图(DBSCAN-VD)生成算法研究。DBSCAN-VD的示意如图4所示,为了便于观察,同一种颜色的点表示通过DBSCAN聚类归纳为一类的点集。图中有五种颜色的小圆,分别代表五类点集,每个点集中的蓝色小点则是代表点集的核心,最后再以点集的核心生成传统Voronoi图。DBSCAN-VD算法就是依据最近邻关系,将这五个点集进行划分。 图4 DBSCAN-VD的简化形式Fig.4 Simplified form of DBSCAN-VD DBSCAN-VD算法通过对生成的点集进行聚类,从而生成若干个点与点之间有密切联系的点集的子集,再在这基础上生成点集的子集的Voronoi图。在通过对该Voronoi图的定义、性质进行研究之后,得出基于DBSCAN聚类的Voronoi图的生成算法。 定义6平面上存在一个点p和一个点集s,定义p到s的距离为p到点集s中最近一点的距离值。 d(p,s)=inf(d(x,p)|x∈s) (1) 定义7平面上存在一个以点集为元素的集合S,S={s1,s2,…,sn},其中si表示一个点集,Voronoi图定义为平面上距离si最近的点的集合。 V(si)={x|d(si,x)≤d(sj,x),∀si∈S,sj∈S,i≠j} S的Voronoi图为: V(S)={V(s1),V(s2),…,V(sn)} (2) 定理1给定平面上的一个集合S={s1,s2,…,sn},其中 (3) (4) 证明: 根据定义6,p0离si最近。再根据定义7,可以得到 p0∈V(si) 所以 另外, 然后 可以得到 所以 因此 □ 定理1实际上是依据Voronoi图的最近邻关系,对点集与点集之间进行划分。上述推导在数学上证明了DBSCAN-VD生成算法的合理性,接下来通过仿真实验来证明算法的正确性。 本文提出的DBSCAN-VD的基本生成算法首先采用自适应参数最优法[14]得出DBSCAN聚类所需的两个参数值Reps和Tminpts,然后对生成的点集进行DBSCAN聚类,找出点与点之间的空间关系,从而将点集划分为若干个点与点之间有密切联系的点集的子集,最后生成聚类后形成的子集的Voronoi图。 DBSCAN聚类的第一步就是确定Reps和Tminpts这两个参数的值[15]。Reps和Tminpts体现了聚类的合理性,从而决定了DBSCAN-VD生成的效果。为了确保聚类后产生的点集的子集规模不过大或过小,本文采用的自适应DBSCAN-VD算法可以自动确定参数值,提高了聚类的准确度。 基于DBSCAN算法,定义密度阈值Tdensity为Reps邻域内存在的Tminpts个数据点,可以得到: (5) 首先定义聚类的“距离”:本文将欧式距离作为聚类距离。计算数据集D的距离分布矩阵,即 Dn×n={Ddistance(i,j)|1≤i≤n,1≤j≤n} (6) 其中:Dn×n为n×n的实对称矩阵;Ddistance(i,j)为数据集D中第i个对象到第j个对象的距离。 Reps参数列表是通过K-平均最近邻法和数学期望法产生的,通过计算数据集D中每个数据点与其第K个最近邻数据点之间的K-最近邻距离,并对所有数据点的K-最近邻距离求平均值,得到数据集的K-平均最近邻距离。第K列的元素构成所有数据点的K-最近邻距离向量DK。对向量DK中的元素求平均,可得到向量DK的K-平均最近邻距离,并将其作为候选Reps参数,Reps参数列表表示为: (7) 然后采用数学期望法生成Tminpts参数列表,再依次求出每个Reps参数对应的Reps邻域对象数量,并计算所有对象的Reps邻域对象数量的数学期望值,作为数据集D的Tminpts参数,表示为: (8) 其中,Pi为第i个对象的Reps邻域对象数量,n为数据集D中的对象总数,最后求解出聚类类别数列表。 根据数据集提取出Reps候选项(按从小到大排列),然后再提取出Tminpts候选项,随后用这些候选项尝试使用DBSCAN算法进行聚类,如果连续的候选项聚类的类别数目相同, 那么选择Reps相对较大的那个作为最终参数输入DBSCAN算法中去。 首先对需要进行空间划分的物体提取二维平面点集,接着以每个点为圆心、Reps为半径的圆来搜索簇,当点p的Reps邻域包含的点数大于Tminpts时,创建一个以p为核心点的新簇。聚类算法依据Reps和Tminpts找出所有核心点,然后分别以核心点为起点,找出由其密度可达的对象生成的新簇,直到遍历完所有点便结束。如图5所示,虚线表示Reps邻域,p1是核心对象,p2由p1密度直达,p3由p1密度可达,p3与p1密度相连。 图5 点集划分处理过程Fig.5 Point set division process 由定理1得到生成算法的具体步骤如算法1所示。 算法1 DBSCAN-VD的生成 图6展现了算法的过程。由图6可以清晰地看出算法的核心思路:首先随机生成点数为5 000的点集,然后对点集进行DBSCAN聚类生成若干个子集,最后用传统Voronoi图算法生成由点集的子集构建的Voronoi图。定理1可以证明该算法思路的正确性。 (a) 聚类图(a) Cluster diagram (b) Voronoi图 (b) Voronoi diagram图6 点集数量为5 000时的Voronoi图生成结果Fig.6 Result of Voronoi diagram generation when the number of point sets is 5 000 F值是一种评价聚类结果的综合指标。设正确率Cprecision为判断正确的数据个数占识别出的数据个数的百分比;召回率Crecall为判断正确的数据个数占实际的数据总数的百分比。则F值表示为: (9) 在聚类结果簇数正确的前提下,密度阈值越小,则噪声率越低,而且聚类结果的F值呈增大趋势。这是由于随着密度阈值的降低,越多的低密度数据点被划分进簇,因此噪声率变低,同时F值的增大则表明准确率增加,聚类结果趋于正确。聚类结果对比如表1所示。 表1 聚类结果对比 从F值评价指标来看,对不同类型的数据集进行聚类,DBSCAN-VD算法均优于对比算法,说明DBSCAN-VD算法具有较高的精确性。 为了证明本文算法的有效性和可靠性,采用Python和OpenCV 2.4.11对算法进行了实现。实验环境为Windows7操作系统,8 GB 内存Intel i5-6500, 3.20 GHz 处理器。 白细胞是人体内血液中的一种细胞,医学上往往检测白细胞的形态和数量作为疾病诊断的依据[16]。正常情况下机体的白细胞数目为4.0×109/L~10.0×109/L。当机体发生炎症等疾病时均会造成白细胞数目的变化, 因此检测白细胞的形态和数量对人体检测疾病来说具有重大意义。血常规检测中,医生根据各个参考值分析白细胞的各个指标,从而对机体进行初步分析[17],具体白细胞的数值与人体机能的关系如下: 1)白细胞计数增多。当人体内的白细胞总数每微升超过10 000个时,一般被诊断为病理性白细胞升高。病理性升高最常见的原因是感染,尤其是细菌感染,感染程度越高,白细胞的数量越大,呈正比关系。 2)白细胞计数减少。当人体内的白细胞总数每微升少于4 000个时,一般会被诊断为病理性白细胞降低。病理性降低最常见的原因是病毒感染,如流行性感冒、病毒性肝炎、水痘等,均能引起病理性白细胞降低。 因此,检测白细胞数目可以为人体疾病的诊断提供依据,白细胞数目的大小也可以反映该疾病的严重程度。 验证过程为:首先从嗜中性粒细胞镜下图片中提取出二维平面点集,如图7所示。 图7 嗜中性粒细胞显微镜下图片Fig.7 Microscope diagram of neutrophils 然后将采集到的点集调用DBSCAN-VD算法,得出结果如图8所示。由图8可知,实例产生了19个Voronoi单元格,在目标对象为大规模嗜中性粒细胞的情况下,DBSCAN-VD算法大大减少了Voronoi单元的数量,更能清晰地观察嗜中性粒细胞群的分布情况,而不是像传统Voronoi图对每一个嗜中性粒细胞进行Voronoi划分。 (a) 聚类后的图片(a) Picture after clustering (b) DBSCAN-VD的划分(b) Division of DBSCAN-VD图8 嗜中性粒细胞显微镜下DBSCAN-VD图Fig.8 DBSCAN-VD diagram of neutrophil under microscope 本文采用该仿真实例对基于集合影响力的多点核心Voronoi图算法进行比较,结果如下: MPUVD(multi-point and unique Voronoi division)算法需要代入参数ε=1.2进行计算(ε为调整点集划分的密度参数,需要人为调整),得出近似优结果如图9所示。实例共计算1 038个采样点,生成了59个多点核心单元格。 图9 MPUVD算法Voronoi划分图Fig.9 Voronoi partition diagram of MPUVD algorithm 本文DBSCAN-VD算法无须输入聚类参数,结果如图10所示。自动生成19个Voronoi单元格,在目标对象为大规模嗜中性粒细胞的情况下,DBSCAN-VD算法大大减少了Voronoi单元的数量,更能清晰地观察嗜中性粒细胞群的分布情况。 图10 DBSCAN算法Voronoi划分图Fig.10 Voronoi partition diagram of DBSCAN algorithm DBSCAN-VD算法的优势有以下几点: 1)采用DBSCAN-VD算法可以减少Voronoi单元的数量,从而提高Voronoi图的生成效率。 2)采用DBSCAN-VD算法可以保证聚类效果的准确性和合理性。 3)DBSCAN-VD算法可以根据离散点分布情况自动生成聚类参数,而MPUVD算法的参数需要多次调试才能获得。 火是引起地球表面异常的重要因素,可以驱使自然界森林、灌木、草原等生态系统植被的演替。植被燃烧过程中的火产生出大量的气溶胶粒子以及各种微量气体,对大气环境和全球碳循环有着重大的影响。如图11所示,本文采用地表火点数据来验证DBSCAN-VD的实际应用效果,地表火点数据来自中国科学院遥感与数字地球研究所研发的SatSee-Fire近实时地表高温异常点查询服务系统。 图11 地表火点数据分布Fig.11 Distribution diagram of surface fire data 验证过程为:首先由地表火点数据分布图找出火点的地理位置,然后提取二维平面中点集,如图12所示。 图12 地表火点数据分布的二维平面点集Fig.12 Two-dimensional plane point set for the distribution of surface fire data 将采集到的点集调用DBSCAN-VD算法,得出结果如图13所示。 由图13可知,实例产生了23个Voronoi单元格,在目标对象为大规模地表火点的情况下,DBSCAN-VD算法大大减少了Voronoi单元的数量,可以更清晰地看出我国地表火点在空间上的划分,由此得到精确的火点高发区域。如图13所示,我国南部、东南亚和西亚是地表火点的高发区域,DBSCAN-VD算法可以提高地表火点的预防和监测效率、精度。 (a) 聚类后的图片(a) Picture after clustering (b) DBSCAN-VD的划分(b) Division of DBSCAN-VD图13 地表火点的DBSCAN-VD图Fig.13 DBSCAN-VD diagram of surface fire 上述嗜中性粒细胞、地表火点的仿真实例充分证明了本文提出的DBSCAN-VD算法突破了传统Voronoi图在划分对象为大规模点集时, 产生图像分割过度的问题。这不仅为Voronoi图发展做出了贡献,也让Voronoi图应用更加广泛。 对于二维数据而言,DBSCAN 算法的基本时间复杂度为O(n2),n为数据集中数据点的数目。自适应DBSCAN算法在DBSCAN算法的基础上进行迭代运算,迭代次数由最优参数对应的K值大小决定,在算法实际运行过程中,K远小于n时,聚类过程即发生收敛。因此,DBSCAN-VD的时间复杂度为O(Knlnn)。Voronoi图的基本时间复杂度为O(nlnn),本文提出的该算法复杂度为O(Knlnn)+O(nlnn)。 综上,本文算法的算法复杂度虽然较传统Voronoi图算法略高,但是提升了聚类的精确性,适用于点集数量较大时生成Voronoi图的应用场景。 目前,传统单点Voronoi图很难适用于大规模数据下的空间划分。本文从大规模点集进行Voronoi图划分时产生Voronoi单元个数过多而导致分割过度的问题出发,提出了一种基于自适应DBSCAN聚类的Voronoi图。通过对显微镜下嗜中性粒细胞、地表火点数据进行DBSCAN-VD仿真,结果可得DBSCAN-VD算法适用于大规模数据下的空间划分,突破了传统Voronoi图单点对单点的一种划分形式,为Voronoi图应用于地理信息系统、生物医学等领域拓宽了应用。在今后的工作中,将从点集的Voronoi图推广到多边形集合的Voronoi图,并且针对Voronoi图尝试改良其生成算法,提高算法的运算效率。2.2 DBSCAN-VD与传统Voronoi图的关系

2.3 DBSCAN-VD的定义

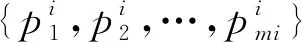
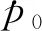
3 DBSCAN-VD的基本生成算法
3.1 DBSCAN聚类参数的确定
3.2 点集划分处理

3.3 DBSCAN-VD生成算法步骤



4 仿真实例及分析
4.1 嗜中性粒细胞的划分




4.2 地表火点的空间划分


5 算法复杂度分析
6 结论

