粮食平房仓底部竖向压力现场试验及离散元模拟
曾长女,李 鑫,范 量,张 斌
河南工业大学 土木工程学院,河南 郑州 450001
粮食是关系国家安全的战略物资,是人民群众的基本生活保障。我国建立了特殊的粮食长期储存制度,建设了大量的粮食储备仓以确保国家粮食安全,这些粮仓中平房仓占很大部分[1]。粮食压力的确定对于粮食平房仓的设计和安全运营具有重要意义。《粮食平房仓设计规范》(GB 50320—2014,以下简称《规范》)中提出,粮食引起的底部竖向压力分布均匀,仅与粮堆高度和粮食容重相关。该理论将粮食作为一种理想的连续性介质,采用流体压力理论计算粮堆竖向压力,但忽略了粮食颗粒的离散特性[2],因而难以反映真实的粮堆竖向压力分布规律。
目前对筒仓侧压力的大小和分布研究较多[3-9]。粮食作为一种典型的散粒体介质,其底部竖向压力分布与预测储粮数量、平房仓设计等都相关。为了能准确掌握国家粮食储备情况,张德贤等[10]通过现场试验建立粮仓底部压力与储粮数量之间的关系,从而对储粮数量进行监测,确保国家储粮安全。在对实仓[11-12]和模拟仓[13-14]的研究中,提出了粮堆底部竖向压力呈非均匀分布,大致呈中间大、边界小的趋势,其不均匀程度随粮堆高度增加而增大,粮堆单点底部压力与粮堆高度之间近似呈线性关系。但由于现场试验具有规模大、费用高、周期长、不易重复进行等缺点,且现场存在较多不确定因素会影响试验结果,导致试验数据有限,难以得到更多实用成果。为了弥补现场试验的不足,部分学者采用离散元数值模拟方法研究。PFC(particle flow code)是一种基于离散元思想模拟不连续物体运动及相互作用的颗粒离散元法,近年来被应用于研究粮仓底部压力。许启铿等[15]、陈家豪等[16]、杨真真等[17]利用 PFC3D软件对散粮堆底部压力进行了模拟分析,研究了粮堆竖向压力、水平压力等底部压力的分布规律。这些研究大多针对粮堆堆积高度、粮堆内部摩擦应力等因素对仓底压力进行分析,而且都采用的是圆形颗粒模拟小麦,不符合实际颗粒形状;此外,对仓底竖向压力影响因素的系统研究也较少。因此,作者以现场试验模型为原型,利用PFC3D离散元方法重现小麦颗粒,并将现场试验结果与模拟现场装料的数值模拟结果作对比,系统分析影响粮堆底部竖向压力的内因和外因,为粮仓底部压力分布的正确描述提供理论支持。
1 粮食颗粒单元改进
2 离散元数值模拟
2.1 数值缩尺模型相似比分析
由于实际模型尺寸大,在数值建模时,若按1∶ 1进行建模会导致数值模型生成的颗粒数量庞大,导致数值模拟无法进行。因此,利用Zhao等[18]提出相似理论来反映不同模型尺寸之间的内在本质联系,建立缩尺模型可较准确地表示原始物理模型的力学行为。
保证建立的原物理模型和缩尺模型的几何尺寸相似,即两个模型的颗粒半径、模型尺寸、颗粒重叠量等按照等比例进行缩放。
式中:Rw和Rs分别为原物理模型和缩尺模型的粒子半径;Lw和Ls分别为原物理模型和缩尺模型的几何长度;uw和us分别为原物理模型和缩尺模型的颗粒重叠量。
建立缩尺模型时,缩尺模型与原物理模型的应力、应变必须保持一致[19]。应力(σ)、应变(ε)可表示:
式中: F(u,R)为相邻颗粒之间所有接触力的合力;D为颗粒特征长度,D=2R;A为颗粒特征面积,A=D2。由式(1)可知,可保证缩尺模型与原物理模型中颗粒应变相等。在三维中,缩尺模型与原物理模型特征面积比值为λA=λ2,则可知缩尺模型与原物理模型的颗粒间接触力的合力比值λF=λ2。
式中:F(u,R)w为原物理模型颗粒之间所有接触力的合力;F(u,R)s为缩尺模型颗粒之间所有接触力的合力。
在离散元中,颗粒的运动方程满足牛顿第二定律[19]。

(4)
在准静态状态下,式(4)中的惯性项可以忽略不计[19],即:
F(u,R)=Q(t)。
(5)
为了保证建立的缩尺模型与原物理模型具有相同的力,则两个模型中对应的力必须相等或相差一个固定倍数[20]。
式中:t为常数;Q(t)w为原物理模型颗粒外部施加的力;Q(t)s为缩尺模型颗粒外部施加的力。
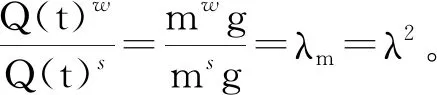

故在缩尺模型中,若将试验模型尺寸等比例缩小λ,则模拟模型颗粒密度应该为原试验模型颗粒密度的λ-1。
2.2 PFC3D模型建立
2.2.1 工程概况
本试验仓是方形平房仓实仓,仓体长45 m,宽28 m,高12 m。根据对称性,选取整个粮仓的1/4作为试验区域,粮食最终装满全仓。在试验区域仓底安装44个振弦式压力传感器和6个重复检测试点监测粮堆底部竖向压力[21]。压力传感器分为4行,在仓壁2距离0.1、9、16 m位置处分别布置间隔为1 m或2 m的3列压力传感器,分别标注为R3、R2和R1。在仓壁1距离7 m位置处布置间隔为1 m或2 m的一行压力传感器,标注为R4。传感器布置如图2所示。在仓底安装振弦式压力传感器,读取稳定初始值,然后开始装粮。装粮时间为每天8:00至23:00,历时5 d完成。装粮完成后静置储存。在试验过程中,每隔0.5 h读取并记录每个压力传感器上的竖向压力值。

图2 现场试验压力传感器的布置
2.2.2 模型细观参数确定
基于上述现场试验以及相似理论,将试验仓尺寸缩小10%进行数值建模,即所建模型的长、宽、高分别为4.5、2.8、1.2 m。为使模型仓达到原型仓所需的重力场,按上述缩尺模型相似比结论,可通过增大散体颗粒的密度来实现,即模型仓中散体颗粒密度为原型仓中颗粒密度的10倍,可使模型仓和原型仓内应力状态一致。
在PFC3D中,颗粒与颗粒、颗粒与墙体相互接触都会产生相互作用[22]。颗粒之间的相互作用通过模拟颗粒间的接触来实现,在每一个特定接触上的本构模型可以分为线性接触模型、接触黏结模型等。线性接触模型适用于无黏性模型,根据粮食颗粒离散性特点,本文中采用线性接触模型,主要细观参数:颗粒法向接触刚度kn、法向与切向刚度比kratio和摩擦系数μ。采用参数标定方法确定颗粒试样的细观参数[23],当模拟值与试验值的应力-应变吻合时,认为当前选择的参数比较合适。表1为PFC3D模型所选用的细观参数。

表1 PFC3D模型细观参数Table 1 Mesoscopic parameters of PFC3D model
2.2.3 储粮过程模拟
建模时,仓壁和仓底采用墙单元表示,粮食颗粒采用颗粒簇clump单元表示。PFC3D提供的测量球命令作为虚拟传感器对底部竖向压力进行测量,测量球半径为0.15m,测量球放置位置如图3a所示,可方便地监测全仓的粮食底部竖向压力。为模拟人工平粮状态,该模型仓内散体颗粒的生成采用在模型底部生成颗粒,在重力作用下让颗粒达到平衡状态,再生成下一层颗粒,如此循环直到达到预定填料高度,散体颗粒上部为平顶。本次数值模拟分4次装满,每层高度分别为0.20、0.40、0.60、0.75m。先在模型顶部生成半径为0.020~0.024m的小球颗粒,再利用颗粒簇clump单元进行替换,最后设定重力场,运行一定时步后,观察最大不平衡力,当其趋近于零时,颗粒堆积稳定密实,开始下次装料,循环重复此过程4次,达到预定高度时停止装料,结果如图3b所示。
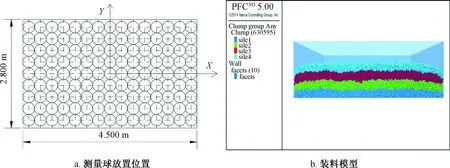
图3 PFC3D建模模型Fig.3 PFC3D modeling model diagram
3 粮食底部竖向压力影响因素分析
在验证模型的基础上,改变影响因素,进一步分析粮堆底部竖向压力分布影响因素。所建模型具有对称性,粮堆竖向压力分布也具有对称性,因此取坐标轴一半进行分析。
3.1 颗粒形状影响
图4所示为球形颗粒、椭球颗粒的底部竖向压力分布。由图4可知,球形颗粒整体趋势与椭球颗粒相近,但椭球颗粒在距仓壁最远位置处的底部竖向压力值较大,在靠近仓壁位置处底部压力值较小,而且随着粮堆高度的增加,距仓壁最远位置与仓壁位置处的底部压力差值越大。对比2种颗粒形状的力链数,球形颗粒的力链数为355 547,椭球颗粒的力链数为562 822,这是由于椭球颗粒比球形颗粒更容易发生自锁现象[24],使椭球颗粒在内部形成能够有效抵御外界的颗粒链,不易受外界影响。

图4 不同颗粒形状对粮堆底部压力
配位数为某一颗粒与其他颗粒接触的颗粒数量,是表示堆积密实度的细观结构参数。不同颗粒形状配位数变化如图5所示。由图5a可知,配位数在X轴上距仓壁距离的增大而增大,与粮堆底部竖向压力分布相对应。将仓底所有测点处配位数取平均值,由图5b可知,随着堆粮高度的增加,颗粒平均配位数随之增加,使粮堆更加密实。模型达到平衡状态时,球形颗粒配位数为6.12,Aparicio等[25]从理论上证明了单一粒径球体准静态下堆积的配位数为6,与本文模拟值相近;椭球颗粒配位数为10.36。由此可知,不同颗粒形状在不同堆粮高度下,其配位数不同,椭球颗粒可以有效增大颗粒的配位数,可以使粮堆在堆积过程中更加密实,不易发生波动。

图5 配位数的变化
3.2 装料方式影响
为模拟装料方式的影响,采用2种颗粒生成方式:一种在模型底部一层一层生成颗粒,如此循环直到达到预定填料高度;另一种在模型顶部生成颗粒,在重力作用下让颗粒下落至仓底,待颗粒平衡后,再生成下一层颗粒,如此循环直到达到预定填料高度。2种颗粒生成方式的椭球颗粒在不同粮堆高度下竖向压力分布曲线如图6所示。由图6可知,顶部生成颗粒方式使底部竖向压力曲线浮动较小,底部竖向压力分布较为均匀;底部生成颗粒方式对底部竖向压力分布影响较大,且受仓壁摩擦系数影响较大。

注:底部生成颗粒简称底颗粒,顶部生成颗粒简称顶颗粒。图7同。
孔隙率、配位数随堆粮高度变化如图7所示。由图7可知,孔隙率随堆粮高度增加而减小,配位数随堆粮高度增加而增加。堆粮高度达到0.75m时底部生成颗粒的平均孔隙率与平均配位数分别为0.392、10.360,顶部生成颗粒的平均孔隙率与平均配位数分别为0.349、11.689。顶部生成颗粒在重力作用下下落至模型仓底部,导致粮堆的孔隙率减小、配位数增大,孔隙率与配位数变化成反比,与齐阳等[26]得到的孔隙率与配位数变化趋势相似。可证明顶部生成颗粒的生成方式使粮堆更加密集、接触力分布更均匀,对粮堆底部竖向压力影响更小。对比这2种生成方式的接触力链数,底部生成颗粒的生成填充方式接触力链数为573 923,而顶部生成颗粒的生成方式接触力链数为688 852,也可证明顶部生成颗粒的生成方式使粮堆更加密集。因此,颗粒生成方式不同,导致粮堆结构的密实状态不同,会影响粮堆底部竖向压力的分布。

图7 孔隙率、配位数随堆粮高度变化
3.3 仓壁摩擦系数影响
考虑仓壁摩擦系数为0.0、0.2和0.4对粮堆底部竖向压力影响,不同仓壁摩擦系数粮堆底部竖向压力分布如图8所示。由图8可知,仓壁摩擦系数为0.0的底部竖向压力曲线波动较大,呈多个波峰和多个波谷状态;仓壁摩擦系数为0.4的底部竖向压力随着距仓壁距离的增加呈增加趋势。由于不同摩擦系数仓壁对颗粒的摩擦作用,导致不同仓壁对粮堆底部竖向压力的影响不同。
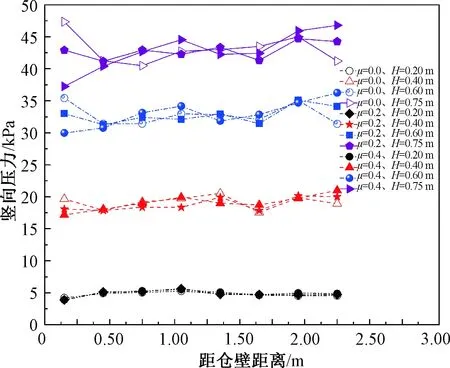
图8 不同仓壁摩擦系数粮堆底部竖向压力分布
X向对称轴中心位置、仓壁位置处底部竖向压力在不同仓壁摩擦系数作用下随堆粮高度变化曲线如图9所示。由图9可知,在模型中心位置处,随着仓壁摩擦系数增大,中心底部竖向压力值增大;在仓壁位置处,随着仓壁摩擦系数越大,边界底部竖向压力值越小。由此表明,仓壁摩擦系数对边界底部压力的分布影响显著,对中心位置处的底部压力影响较小,底部压力分布与仓壁摩擦系数、距离仓壁距离有关,与文献[16]的结论相似。

图9 X向对称轴中心位置、仓壁位置底部压力随堆粮高度变化
4 现场试验与数值模拟结果
结合上述粮堆底部竖向压力的影响因素分析,在仓壁摩擦系数为0.4的模型仓顶部生成椭球颗粒,在重力作用下下落至模型仓底部,并将数值模拟与现场试验结果进行对比分析。数值模拟与现场测点数据结果对比如图10所示。模拟采用的测量球半径较大,并非与现场试验布置的传感器位置一一对应,因此会产生偏差。利用《规范》中粮堆竖向压力公式pvk=γh( γ 为粮食容重,kN/m3;h为堆粮高度,m)计算最大粮堆高度下底部竖向压力值作为理论值,由图10可知,《规范》获得的理论值均比现场试验测试值和数值模拟值大。随着距垂直仓壁距离的增加,数值模拟与试验监测的粮堆底部竖向压力均先逐渐增加,之后达到稳定状态。就整体趋势而言,数值模拟的底部竖向压力值与试验值具有相同的变化趋势,可利用本文建立的模型进行粮堆底部竖向压力变化趋势研究。

图10 数值模拟与现场试验对比分析
为了定量地表述仓底粮食竖向压力分布规律,采用压力分布系数表述不同位置处粮堆底部竖向压力。定义压力分布系数λV为各测点位置粮堆底部竖向压力(V)与对应列中最大的粮堆底部竖向压力值(Vmax)之比。
由图11可知,压力分布系数λV随距离垂直对应仓壁距离的增加而增加,在垂直对应仓壁0~4m范围内压力分布系数增长较快。在对应仓壁大于8m后,两个测点之间压力分布系数大部分在0.9~1.0之间,增长幅度较小,因此该位置处仓壁对粮堆底部竖向压力影响较小。需要说明的是,本现场试验中靠近中部3个点有异常,主要是受中间柱等因素的影响。

图11 现场试验底部粮食竖向压力分布系数
将现场试验R3、R2、R1和R4列的数值模拟结果与文献[16]数值模拟结果对比,如图12所示。压力分布系数λV随着距离相应壁面距离的增加而逐渐增大,随后又缓慢下降逐渐趋于稳定。距仓壁0~5m范围内,压力分布系数增长较快,与文献[16]增长趋势相同;距仓壁8m左右,增长幅度较小,逐步趋于稳定,与现场试验结论相似。

图12 数值模拟底部粮食竖向压力分布系数
由现场试验和数值模拟试验可知,距仓壁距离对仓底粮食压力分布影响较大,根据上述分析,粮仓与粮食之间摩擦系数、装料方式、颗粒形状等都会对粮堆底部竖向压力产生影响,显然装料方式、仓壁摩擦系数影响更大,尤其是仓壁摩擦系数的影响获得了众多学者的关注。由本文的试验可得,在试验范围内,距仓壁距离大于8m后,墙体对粮食底部竖向压力的影响就很小了。整体而言,现场试验结果比数值模拟结果大,且这两者结果均小于《规范》推荐的理论值,有必要积累更多的现场数据,对现有规范相关内容进行适当的修正。
5 结论
以现场平房仓装料试验为基础,利用PFC3D软件对平房仓进行数值模拟,研究了颗粒形状、仓壁摩擦系数和装料方式对粮堆底部竖向压力分布的影响。
离散元软件PFC3D建立的椭球颗粒能更好地模拟小麦在填料过程中粮堆底部竖向压力变化趋势。球形颗粒配位数为6.12,椭球颗粒配位数为10.36,椭球颗粒更容易发生自锁现象。颗粒不同的生成方式会影响粮堆结构的密实状态,从而影响粮堆底部竖向压力的分布。顶部生成颗粒方式会导致粮堆孔隙率小、配位数大,使得粮堆更加密集。
粮堆底部竖向压力分布与仓壁摩擦系数以及距离仓壁距离有关。不同仓壁摩擦系数对仓底竖向压力分布影响不同,仓壁摩擦系数越大,对边界底部压力的分布影响越显著,对中心位置处的底部压力影响越小。
压力分布系数能很好地表示不同位置处粮堆底部竖向压力的分布情况。压力分布系数在仓壁处较小,随距仓壁距离的增加而逐渐增大。现场试验和模拟试验均表明在距仓壁距离小于5m的范围内,压力分布系数增长较快,到达8m后压力分布系数趋于稳定。
本文获得的现场试验和数值分析结果,将为今后规范修订仓底压力提供可靠的理论依据。
致谢:感谢云南省粮油工业有限公司为试验提供帮助。

