惯性稳定平台高精度控制方法*

于子航，王改云

（桂林电子科技大学，广西 桂林 541000）

0 引言

惯性稳定平台的精度对于系统性能的影响重大，特别是在军用侦察、卫星成像等远距离应用中，光学视轴的微小抖动都会造成CCD 成像模糊，因而对于稳定性的要求非常高［1-2］。传统的惯性平台驱动一般采用直流力矩电机。但直流力矩电机的体积大、散热差，并且采用机械换给系统带来了一些高频干扰，降低了系统的可靠性［3-4］。相比较来说，永磁同步电机（PMSM）为三相交流驱动，采用电换向，并且其转矩密度大，体积小。因而越来越多的高精密惯性平台采用PMSM 作为驱动电机，以给平台留出更多的有效载荷空间。

基于经典控制理论的线性控制器难以满足当前系统的高精度需求。近些年来，各种控制策略被用于PMSM 的调速系统中。比如利用迭代学习对重复性扰动抑制的高效性，文献［5］设计了空间域的迭代学习控制器用于抑制PMSM 的齿槽力矩。针对电流检测误差，文献［6-7］详细分析了其对于系统的影响，文献［8］设计了测量误差观测器来实时观测和补偿。

以上的控制方法虽然都取得了一定的效果，但也存在各自的问题。比如迭代学习控制器比较占处理器的内存，而针对电流环的误差观测器设计比较复杂。

对于调速系统的主控器，文献［9-11］采用了自抗扰控制，取得了较好的效果。然而仍然存在设计复杂、参数较多难以整定的问题。文献［12］设计了模型参考自适应控制，但对于PMSM 这类模型实际工作中变化不大的系统，模型参考自适应难以取得满意的效果。

近些年来，滑模变结构控制（SMC）因其较强的鲁棒性和设计简单的特点，被广泛用于各类电机的调速控制中［13-16］。但基本的滑模控制抖振严重，而若调整参数减小抖振又必将使得系统状态趋向于滑模面的速度过慢，从而导致系统响应速度慢。对于基本滑模控制存在的弱抖振和快趋近速度之间的矛盾，文献［17］设计了一种指数趋近律，其切换增益是关于系统状态的函数，使得系统状态可以快速到达滑模面，但系统状态在滑模面上依然抖振很大。文献［18］在传统趋近律基础上，设计了一种可变增益的趋近律，达到了削弱抖振的效果，但当系统状态趋近滑模面时，切换增益迅速减小，使得系统状态趋近滑模面的速度很慢，系统的鲁棒性差。

基于以上背景，本文设计了一种新型滑模控制器，有效减小了抖振并提升了速度跟踪性能。同时，为进一步削弱系统抖振并抑制电机工艺缺陷、驱动控制电路缺陷以及外部实时扰动，将系统所受外扰扩张为系统的一个状态，设计Luenberger 状态观测器对外扰进行观测，并将观测到的扰动补偿进系统中。

1 PMSM 的数学模型

PMSM 调速系统的基本控制策略中应用最广泛的是直接转矩控制和矢量控制。直接转矩控制在实际应用中存在磁链观测困难、非线性振荡和参数摄动等问题，因而难以实现高精度控制。本文采用矢量控制。矢量控制通过坐标变换的方法将电流分解成相互垂直的转矩分量和励磁分量，然后进行独立的控制。

矢量控制将施加在电机上的ABC 三相电流变换成旋转dq 两轴上的电流。控制d 轴电流为0 即可实现解耦，此时电机输出力矩与q 轴电流成正比。

在忽略电机制造工艺缺陷的前提下PMSM 的数学模型可表示为：

2 新型滑模控制器的设计与实验

由于系统受各种扰动的影响，传统的滑模控制器必须增大控制器系数以满足可达性条件。然而系数的增大会使得系统状态不断地穿越滑模面，从而导致系统抖振。由于抖振频率较高，很容易使得系统不稳定［19-20］。在平台实际工作中，抖振还容易对轴系造成不可逆的物理损伤，降低平台的寿命。

为此，本文设计了一种新型的滑模控制器。

为证明所提出的新型SMC 相比于传统SMC 和PI 控制器的优越性，设计了匀速跟踪实验对各控制器性能进行了对比。在实验中不额外施加其余外扰，确保各实验中系统的工作环境一致，匀速跟踪实验能较好地反映系统在齿槽力矩和摩擦力矩的干扰下速度跟踪的性能。

2.1 新型滑模面的设计

由第1 节的PMSM 数学模型可得PMSM 的运动方程为：

定义角速度误差e=ω-ωd，其中，ωd为角速度给定值。代入上式中可得：

定义滑模面：

其中，f 为反馈系数且f >0。

此时系统状态完全由滑模面所确定。根据线性系统理论，当式（4）代表的系统极点均在复频域的左半平面上时，角速度误差e 将在有限时间收敛到0。参数f 决定了e 的收敛速度。

2.2 控制律的设计

在式（5）的基础上，设计如下控制律：

从而，所设计的控制律满足滑模可达性条件。无论系统状态如何，以上设计的滑模控制器都可以使系统输出角速度误差在有限时间内收敛到0。

2.3 新型滑模控制器实验

在已有的实验平台上进行实验。平台所使用的PMSM 参数如表1 所示。

表1 平台电机参数

对扫频获得的系统模型进行拟合可得系统速度环被控对象的名义模型为：

根据前文所提策略对实验平台设计新型滑模控制器。对比实验分别采用PI 控制器和传统SMC控制器。控制器参数如表2 所示。

表2 控制器参数

实验条件为10°/s 匀速跟踪。实验结果如下页图1 所示。

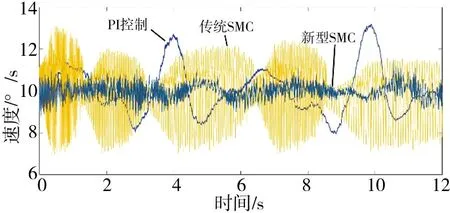
图1 基本控制下的匀速跟踪曲线

由实验结果可见，齿槽力矩对PI 控制器的影响很大，由于鲁棒性太弱使得PI 控制器的收敛速度很慢，速度跟踪误差最大值达到了3°/s。传统的SMC虽然能很快收敛到给定值，但其抖振十分剧烈，并且速度误差也超过了2°/s。相比较来说，本文提出的新型SMC 在保证较小的跟踪误差的同时具有很小的抖振，其速度跟踪误差不超过1°/s。证明了提出的新型SMC 的有效性。

3 扰动抑制

虽然本文提出的新型滑模控制器可以提高系统的跟踪精度，但由于控制律中包含有符号函数项，因而仍存在抖振。抖振主要来源于系统的外扰，当系统状态到达滑模面时无法停留在上面，而是不断地在滑模面上下穿越，在表达式上的反映就是符号函数项的值不断地突变。采用饱和函数替代符号函数可以一定程度上削弱抖振，但仍然难以从根本上解决问题［21-22］。

为此，本文采用扰动观测与补偿的方法减小滑模控制器的抖振，同时抑制外部扰动对系统的影响，提升系统的跟踪精度。

在Simulink 中搭建了仿真系统，对施加的扰动进行观测。设计了25 Hz 的正弦扰动观测，以测试观测器的带宽和相位滞后程度；设计了三角波扰动的观测，以测试观测器对于宽频带复杂扰动的观测效果。

3.1 Luenberger 观测器的设计

由式（2）得：

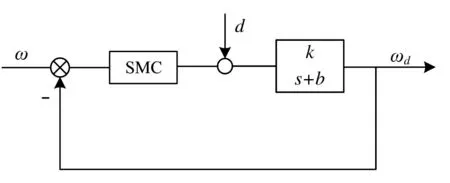
图2 速度环等效框图

为观测出系统的等效扰动d，将d 扩张成为系统的一个状态：

设计Luenberger 状态观测器：

反馈矩阵E 用来配置的特征值（A-EC）。由上式可见，（A-EC）的特征值为负时，观测误差可在有限时间收敛到0。并且由式（18）知特征值的绝对值越大，则收敛速度越快，观测值能迅速跟踪实际值，即观测器的带宽越宽。但观测器带宽越宽则会在观测到的扰动中引入越多的高频噪声，反向补偿进系统后容易造成系统颤振甚至不稳定。由于实际平台工作中一般安装有减振器，传递到平台的扰动频率基本都在20 Hz 以下，因而所设计的扰动观测器带宽达到25 Hz 即可抑制绝大部分外部干扰，并且可保证系统的稳定运行。

3.2 观测器的仿真实验

由上述分析可知，矩阵（A-EC）的特征值决定了观测器的带宽。在仿真实验中调整（A-EC）的特征值，使得观测器带宽设定为25 Hz，得到反馈矩阵E 的取值为：

在Simulink 中搭建仿真，分别给系统施加幅值0.2 A 频率25 Hz 的正弦扰动和幅值0.2 A 频率5 Hz的三角波扰动。观测到的扰动与实际施加的扰动d 对比曲线如下页图3～图4 所示。

图3 正弦波扰动观测仿真曲线

图4 三角波扰动观测仿真曲线

从仿真曲线可见，在25 Hz 正弦波观测中，观测器增益约为0.7，满足带宽25 Hz 的要求。在三角波扰动观测中，除速度突变处由于相位滞后导致误差较大外，其余绝大部分时间内观测误差的绝对值均小于0.01 A，即实际扰动的95%可以被所设计的观测器观测到。

以上仿真实验证明了所设计的扰动观测器具有较好的性能，满足本系统的要求。

4 复合控制器的设计及实验

4.1 复合控制器设计

本文在第3 节中设计了一种新型的滑模控制器，但由于外扰的存在，参数l 的值设置得很大，以满足滑模可达性条件，确保系统的稳定性。但参数l的增大会使得角速度跟踪误差收敛速度较慢，从而降低了系统的跟踪精度。

而本文在第4 节中设计了一种扰动观测的方法，使得外扰的值可被估计出来，从而补偿进滑模控制器中，以减小l 的值，降低SMC 的抖振，同时抑制外扰对系统的影响。

在式（7）的基础上设计扰动补偿后的SMC 控制律可表示为：

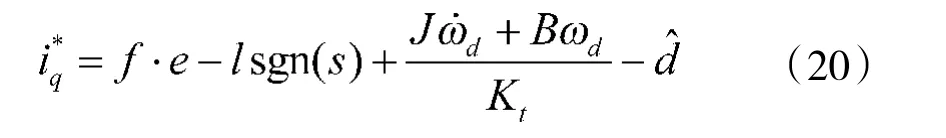
由于外扰d 中的大量低频分量被观测器观测并补偿，因而控制器的参数l 可设成较小的值。在实际系统中，l 取值改为0.06 即可保证系统稳定。

基于新型复合控制器的PMSM 场矢量控制框图如图5 所示。

图5 基于复合控制器的系统框图

4.2 复合控制器的实验

本实验平台的主控芯片为DSP（TMS320F2812），采用FPGA（EP4CE6F17C8）作为辅助控制器分担主控器的压力。电流环频率为10 kHz，速度环频率为1 kHz。通过14 位高精度磁编码器测量电机的机械角位置，16 位微机械陀螺仪测量平台相对于惯性坐标系的角速度。

对比实验采用的控制策略为传统的PI+DOB。分别比较10°/s 的匀速跟踪及幅值10°/s 频率1 Hz的三角波跟踪条件下两种控制策略的跟踪精度。

其中匀速跟踪反映了系统对于稳态指令的复现精度，可以较好地反映系统抵抗外扰的能力。而三角波指令中包含了各频率分量，可以较好地反映系统对于复杂的宽频带指令的复现能力，表征系统的带宽和响应速度。

对于惯性稳定平台，评价系统精度的指标为电机相对于惯性坐标系的位置误差，即速度误差在时域上的积分：

所有的控制器参数均调至保证系统稳定条件下的最优值。为保证可重复性，每组实验均重复3次。得到的典型实验结果如图6 ～图7 所示。每组曲线的上图为速度曲线，下图为位置误差曲线。

图6 匀速跟踪及位置误差对比

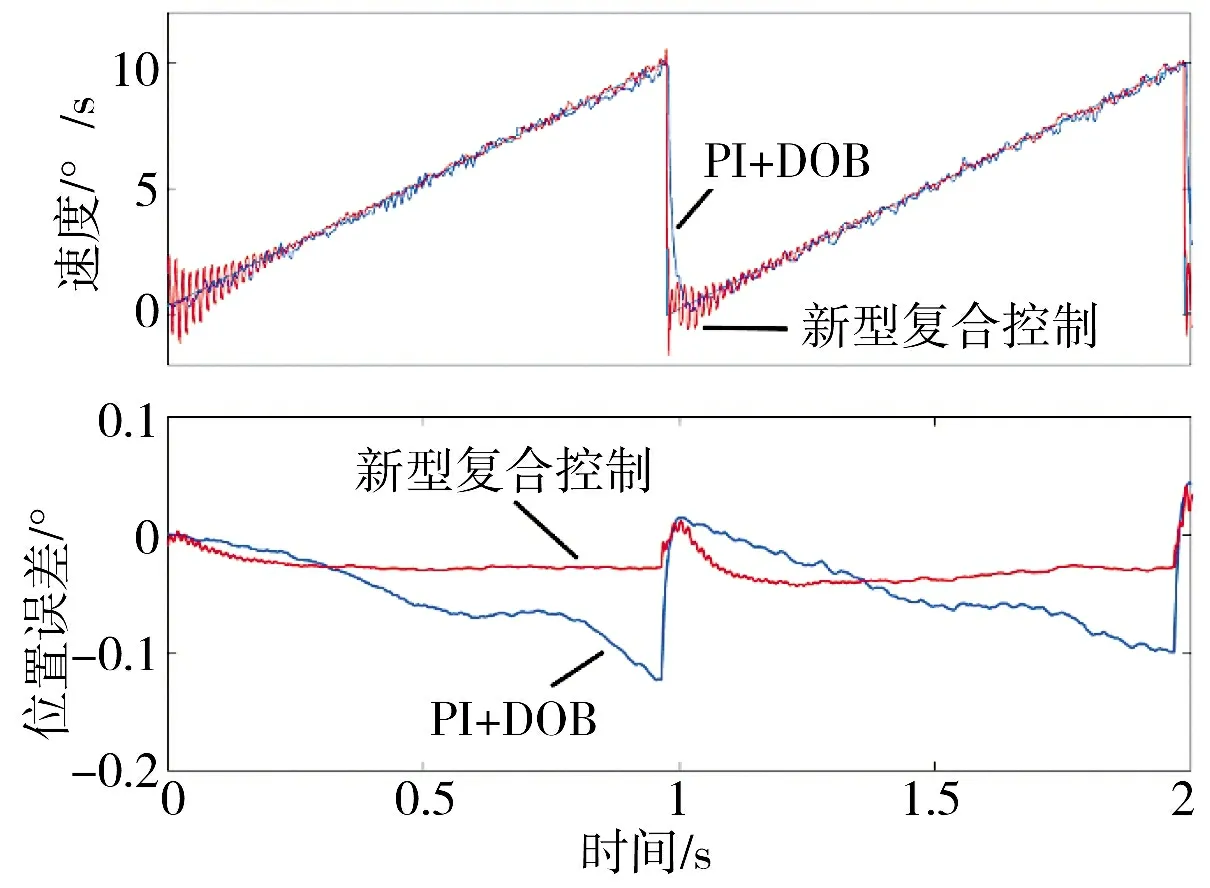
图7 三角波跟踪及位置误差对比

对数据进行分析。计算位置误差绝对值的平均值及RMS 值，结果如表3 所示。

表3 位置误差平均值及RMS 值对比

4.3 实验结果分析

由以上实验结果可见，采用本文提出的新型SMC+扰动观测器的复合控制方案，可以显著提高系统的跟踪精度。在匀速跟踪实验中，新型控制方案的位置误差平均值仅0.006 32°，约传统PI+DOB方案的1/3。在三角波跟踪实验中，新型控制方案的位置误差RMS 值仅0.023 1°，约为PI+DOB 的一半。

5 结论

针对传统SMC 存在抖振剧烈的问题，本文提出了一种新型SMC，实验结果证明新型SMC 可以减小系统抖振，提高速度跟踪精度。鉴于所提出的新型SMC 仍然存在抖振问题，对外扰抑制能力不强，本文将外扰扩张成为系统的一个状态，设计了Luenberger 状态观测器对外扰进行观测，并将观测到的扰动补偿到所提出的新型SMC 中，进一步削弱了系统的抖振，并且提高了系统抵抗外扰的能力。匀速跟踪及三角波跟踪的实验结果证明，所提出的复合控制方案，相对于传统PI+DOB 方案的跟踪误差更小，特别是在匀速跟踪实验中，位置跟踪精度提高了约3 倍。证明了本文提出的新型复合控制方案为一种简单、高效的控制策略。