基于改进GA-BP 神经网络的目标毁伤效果评估*

张宗腾，张 琳，谢春燕，张 搏，杨博帆

（1.空军工程大学防空反导学院，西安 710051；2.解放军95835 部队，新疆 马兰 741700；3.空装驻上海地区第一军代室，上海 200235）

0 引言

目标毁伤效果评估起源于第一次世界大战，早期多以人工判读的方式评估目标毁伤情况，其工作效率较低［1］。伴随着高新武器装备的研发、信息化战场环境日趋复杂多变，以及“蜂群”作战理念的突显，在实施火力打击后，能否及时准确地对目标毁伤情况做出判断，将在很大程度上影响后续作战任务的执行，并直接关系到新一轮火力打击的制定。因此，对目标毁伤效果评估已成为作战目标选取、打击和再调整的重要环节，不仅能够为指挥员提供正确的决策依据，而且能够最大限度地优化火力、提升作战资源利用率。

目前，国内外研究人员对目标毁伤效果评估进行了不同程度的研究。文献［2-3］利用层次分析法建立评估模型，虽然系统性强、模型简洁清晰，但在定性与定量分析时，主观性大、定量数据少；文献［4-7］中模糊综合评判法能够将定性评估有效地转为定量评估，但是复杂性关联指标的权重仍是主观化的设定；文献［8-10］的贝叶斯网络则利用直观的图形结构，具备很好的推理和计算能力，但在推理信息较少或缺乏时，无法精确获得评估结果；文献［11-12］神经网络能够较好地实现非线性映射、具备模糊推理和泛化能力、计算单元简单且易于实现，但其自身易陷入局部最优困境，并且在多维变量下收敛速度较慢。

由于目标系统复杂度高，其毁伤效果评估各指标关联耦合性较强，且考虑到评估时效性的需求，因此，选用典型BP 神经网络为基础进行评估。由于典型BP 神经网络易收敛陷入局部最小值且需多次测试，遗传算法（Genetic Algorithm，GA）具备其并行、高效和全局搜索的特点，二者融合的GA-BP 神经网络更适用于目标毁伤效果评估。但是典型的遗传算法在一定程度上会出现较早收敛等问题，为有效发挥其优势，本文对该算法加以改进，提出了改进GA-BP 神经网络模型。并以飞机系统为例，使其在确保较高的评估可信度和准确度前提下，避免了模型陷入局部极小值，提升了模型泛化能力，从而实现目标毁伤效果评估。

1 飞机系统毁伤模型

1.1 目标毁伤树

目标毁伤树是一种采用演绎式分析方法，从目标系统层（顶事件）开始，自顶向下、逐级分析系统、子系统、部件、单元等相互影响关系，并构造形成特殊的倒立树状逻辑关系图。同时，参考美军目标毁伤评估常用的“三段式”方法［13］，首先是确立目标系统层的总体评估对象；然后是功能毁伤层将评估对象按照子系统功能划分为若干子功能系统；最后是分析物理毁伤层的相关部件毁伤（基层事件），并按照重要程度区分和确定关键重要部件。

根据飞机系统总体和子系统的功能特征分析，将飞机系统划分为平台总体、动力推进、通信导航、载荷操控、综合防护等5 个子功能系统。考虑到飞机系统的复杂性，对毁伤树进行简化合并（例如，将起落装置、环控设备等并入机身，将UHF 电台天线、GPS 天线等并为机载天线），并选取3 个较为关键的子功能系统，进行目标毁伤分析如图1 所示。

图1 飞机系统毁伤树

1.2 毁伤等级划分

经调查研究，并查阅国内外相关文献资料，通常将飞机系统的毁伤级别［14-15］划分为：KK 级、K级、A 级、B 级、C 级、E 级。考虑到目标毁伤不仅体现在物理毁伤层面，而且还应重点体现在目标功能毁伤层面，毁伤等级以目标子系统功能毁伤程度来划分。在此基础上，根据目标功能毁伤程度对毁伤等级进行判定。同时，结合单位工作实际经验和专家意见，为便于战场目标毁伤效果评估，本文将目标毁伤分为4 个等级，见表1，即无损毁伤、轻度毁伤、中等毁伤、严重毁伤。

表1 目标毁伤等级判定

2 改进GA-BP 神经网络模型

利用上一章所构建的系统毁伤模型作为输入，为实现目标毁伤效果评估，本文提出了改进GA-BP神经网络模型，并通过MATLAB 软件实现该模型的编程，其设计流程图如图2 所示。

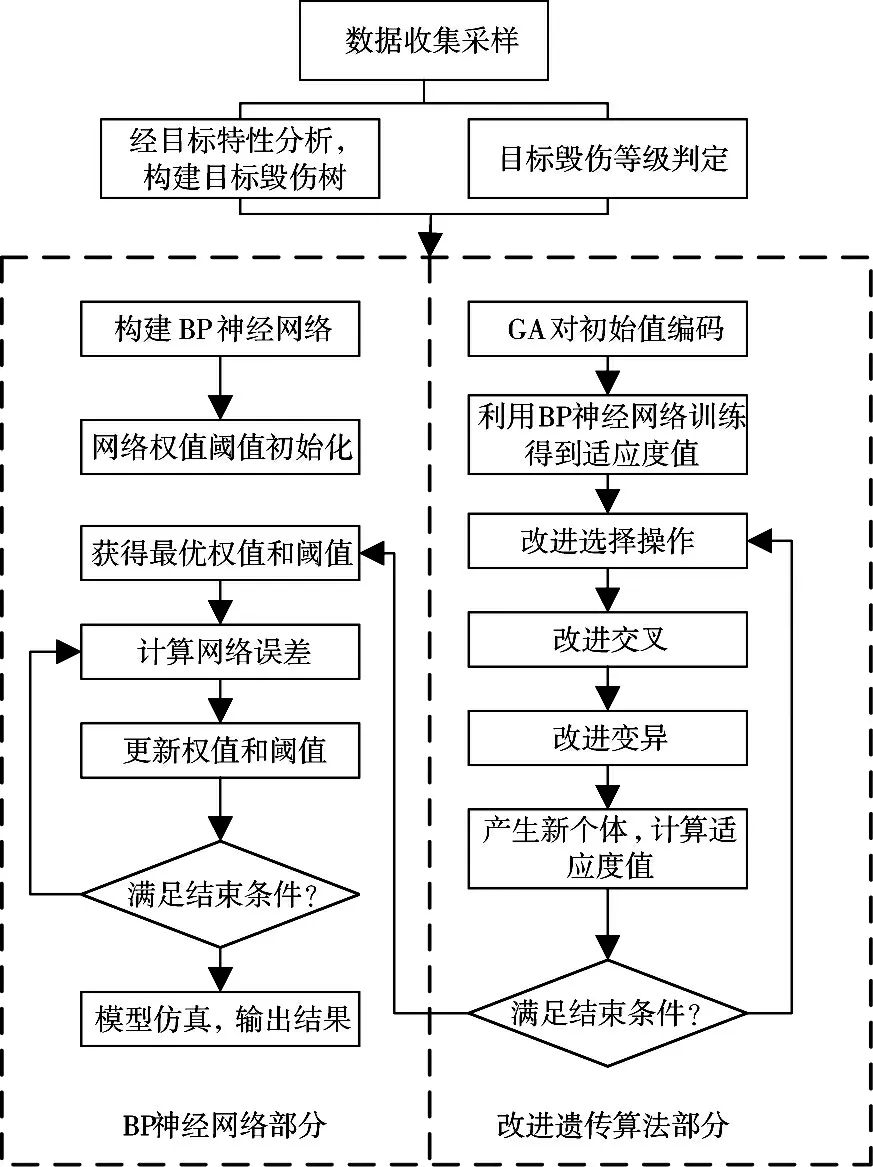
图2 改进GA-BP 神经网络模型流程图

该模型利用经典BP 神经网络所拥有的良好容错和非线性映射能力，并充分结合遗传算法可以广泛搜索空间并寻求全局最优解的特点，两者优势互补、有机融合，具体操作步骤如下：

1）根据目标毁伤树的物理毁伤层、目标系统层分别确定神经网络的输入和输出节点数，并邀请相关领域专家，依据目标毁伤等级判定标准进行评分，生成网络模型训练与测试数据集；

2）构建BP 神经网络，并初始化相关权值、阈值和函数，通过遗传算法演化训练神经网络，以获得最优权值和阈值；

3）利用演化训练得到的最优权值和阈值进一步优化BP 神经网络，以得到满足精度要求的BP 神经网络。

2.1 BP 神经网络

BP 神经网络通常由输入层、隐含层和输出层等组成，并按照网络输出层与期望间误差最小的原则，从输出层经隐含层，再反馈至输入层，修正各层神经元的阈值和权重值［16］。一个典型的3 层BP 神经网络即能实现对任意非线性函数的逼近，其结构如图3 所示。

图3 典型3 层BP 神经网络结构图

若隐含层到输出层的传递函数f（·），输出层的传递函数为g（·），则输入层的输出为：

隐含层的输出为：

输出层的输出为：

此时，神经网络的输出值与期望值的误差为：

式中，n、r、m 分别为输入层、隐含层、输出层的神经元个数，wij、wjk分别为输入层节点i 与隐含层节点j的权值、隐含层节点j 与输出层节点k 的权值。

2.2 改进的遗传算法

2.2.1 染色体编码和种群初始化

由于本文使用的数据集合中多为浮点数，且预测精度要求较高，因此，采用实数编码的方式对各网络节点权值进行编码，并设定权重的阈值为区间［-1，1］的随机数。其中，染色体编码的长度l 为：

式中，n、r、m 分别为输入层、隐含层、输出层的神经元个数。

同时，为避免遗传算法陷入局部最优解，降低算法复杂程度，一般种群规模在20～200 之间，这里设置种群规模为30。

2.2.2 适应度函数设置

适应度函数是用来评估个体优劣程度的函数。由于遗传算法在进化搜索中基本不依赖外部信息，所以作为唯一的评判依据，更应选取合理恰当的适应度函数，通常适应度函数为［17］：

式中，a、b 为常数，f 为搜索目标函数。由于本文所使用的遗传算法为单目标函数，且BP 神经网络为单输出节点，因此，这里的适应度函数为：

式中，yi、zi分别为神经网络的输出值与期望值。

2.2.3 改进的选择算子

遗传算法中常用的选择算子为最优个体保存法，即直接将适应度最高的个体复制给下一代。该方法虽然避免了最优个体被淘汰的风险，但在一定程度上忽视了种群的多样性。因此，针对该问题并结合以概率为基础的适应度比例法，本文提出一种新的选择算子，其操作过程为：

1）计算初始种群中各个个体的适应度；

2）根据个体适应度，将其从高到低依次排列，并分为高、中、低三档；

3）对高档和中档个体直接复制一份遗传到下一代；

4）从高档和低档中按照各50%的比例原则随机选择并复制到下一代中。

这样在很大程度上提高了算法的选优能力，同时还保持了种群的多样性。

2.2.4 交叉、变异算子

遗传算法中的交叉和变异操作，是保持种群良好性和多样性的重要环节。其中，第i 个染色体Xi和第j 个染色体Xj在k 位进行交叉操作的公式为：

式中，a 为区间［0，1］的随机数。

若选择个体i 的第j 个基因X 进行变异操作的公式为：

式中，Xmax、Xmin分别为基因X 的上界和下界，r1为区间［0，1］的随机数，r2为一个随机数，t 为当前进化次数，Tmax为最大进化次数。

2.2.5 改进的自适应交叉、变异概率

为避免群体陷入局部最优解，Strinvinas［18］等曾提出了自适应的交叉率（Pc）和变异率（Pm），其公式为：

其中，fbig为交叉的个体中适应度较大的值；fmax为种群中个体适应度最大的值；favg为种群个体平均适应度值；f 为当前需要变异的个体适应度值。

由式（10）、式（11）可知，虽然此方法比较适合于进化后期的种群，而在进化初期演化的不太理想，因为适应度高的个体几乎不参与前期的交叉和变异，易使遗传算法种群进化陷入局部最优解困境。因此，这里提出一种改进的自适应交叉、变异概率公式，提高了进化前期的个体交叉和变异概率，加速了遗传算法收敛速度，具体公式如下：

3 实验结果和分析

3.1 数据集

利用某红蓝对抗模拟仿真平台，根据图1 采集飞机系统各部件毁伤数据共20 组。并邀请10 名领域专家、高工、技师依据表1 对飞机系统各部件毁伤程度评分，再通过模糊加权合成的方法计算获得各部件和系统总体的毁伤程度值，如下页表2 所示。

表2 飞机系统各部件毁伤程度

其中，前16 组为训练数据，用于训练神经网络节点权重值；后4 组为测试数据，用于验证模型有效性。

3.2 试验仿真及结果分析

本文根据试验样本特点，选用单隐层的BP 神经网络，并依据飞机系统毁伤树见图1，确定其输入层和输出层节点个数分别为10 和1，隐含层激活函数为‘Tansig’，输出层激活函数为‘Purelin’，网络采用贝叶斯正则化算法‘Trainbr’训练网络，学习率为0.000 1，目标误差为0.001。

同时，隐含层节点数量多少直接影响BP 神经网络的训练性能，然而隐含层节点数的确定尚无理论指导［19］，一般采用经验式（14）确定。经反复测试，本文设置隐含层节点个数为12。

式中，n、r、m 分别为输入层、隐含层、输出层的神经元个数；α 通常取0～10。

通过MATLAB 对改进GA-BP 神经网络模型进行仿真，其均方误差曲线和平均适应度曲线如下页图4、图5 所示。综合两个曲线可以看出，改进GA-BP 神经网络在迭代至第20 代左右，网络均方误差和适应度都得到了快速收敛，并稳定至某一较小区间内。

图4 均方误差曲线

图5 平均适应度曲线

并且通过图5 还可观察得到，虽然模型在迭代至第20 代时，已经拥有了较高的适应度值，但是由于遗传算法中加入了改进的选择操作、交叉和变异算子，在不破坏种群稳定性的同时，最大程度上保持了种群的多样性，提升了模型的泛化能力和全局搜索寻优能力。

同时，为进一步验证改进GA-BP 算法的评估精准度，本文将GA-BP 算法和BP 算法也进行了仿真，其仿真结果如图6 所示。通过三者与实际数据的直观对比，IGA-BP 模型更加接近实际值曲线。并且通过计算3 种模型的平均绝对误差和平均相对误差发现（见表3），传统的BP 算法和GA-BP 算法在精度方面均低于改进后的GA-BP 神经网络模型。

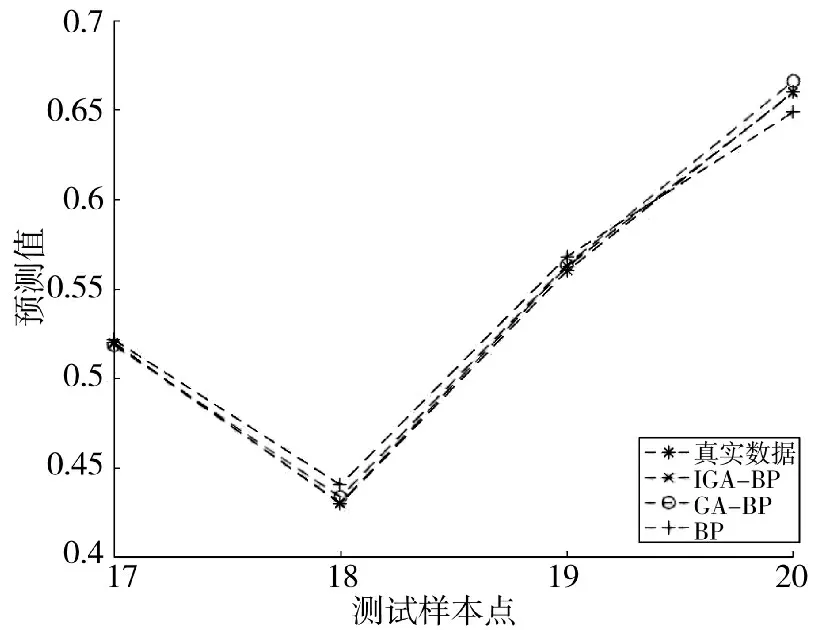
图6 评估结果比较图

表3 误差精度比对表

4 结论

本文提出了一种基于改进GA-BP 神经网络模型，并将其引入到目标毁伤效果评估领域，可应用于已知打击目标相关信息数据条件下的红蓝对抗演习演训评估任务。文中以飞机类复杂系统为例，在构建目标毁伤树和划分毁伤等级的基础上，针对传统遗传算法中选择操作、交叉和变异概率加以改进。同时在保证模型稳定性的基础上，最大程度地提升了种群的多样性，增强了模型的泛化能力和全局寻优能力。最后通过算例仿真并与现有算法相比较，验证了模型的收敛性和准确性。该模型可为演习演训攻防双方目标毁伤效果评估和战场损伤评估提供一定的辅助决策支持，对目标毁伤效果评估的人工智能化方面的发展具有一定的启发和借鉴意义。