块截断编码的图像自嵌入半脆弱水印算法

王艺龙，李震宇，巩道福*，马世鑫，刘粉林

1. 中国人民解放军战略支援部队信息工程大学， 郑州 450000； 2. 中国人民解放军国防大学， 北京 100091

0 引 言

数字图像作为获取及传播信息的主要载体，给人们的生活带来极大便利，但其易被编辑、修改的特点也带来了一系列安全隐患。人们为了达到某种目的，可以利用图像处理工具对图像进行篡改。因此对数字图像的内容进行真实性判断，并恢复被篡改的内容是当前的研究热点。

数字图像自嵌入水印技术是解决此类问题的主要技术手段之一，其将图像的内容信息进行压缩编码，并嵌入到图像中，通过比较篡改前后图像水印的变化情况进行完整性认证，依据嵌入的内容信息实现篡改恢复。现有的自嵌入水印技术主要分为脆弱水印方法和半脆弱水印方法两类。脆弱水印研究主要关注认证粒度和嵌入强度等，如Singh和Singh(2016)提出了一种基于离散余弦变换(discrete cosine transform, DCT)系数的自嵌入水印算法，该算法将图像分为块，对每个块基于DCT变换生成2 bit认证水印和10 bit恢复水印。Tong等人(2013)提出了一种基于混沌映射的脆弱水印算法，将图像分为2×2块，取每个块均值的高5 bit，并找到每个块的同伴块，也取块均值高5 bit，将10 bit作为恢复水印。通过10 bit的恢复水印得到2 bit的认证水印，利用混沌映射找到映射块并将水印嵌入该块像素的最低3 bit中。Rakhmawati等人(2018)提出了一种基于双认证的自嵌入水印算法，该方案将图像分为2×2的块，用块均值的高5 bit作为恢复水印，依据恢复水印生成两份认证水印，并将恢复水印和认证水印嵌入到映射块中。Enugula等人(2020)提出了一种基于自嵌入脆弱水印算法的图像安全方案，该算法将图像进行2×2分块，并依据每个块的均值产生4 bit认证水印和8 bit恢复水印，并将水印嵌入到映射中。这类算法嵌入水印使用了像素的最低3 bit，对原图质量影响较大。Ansari等人(2016)提出一种基于奇异值分解(singular value decomposition, SVD)的脆弱水印算法，该算法将图像分为4×4的块，并依据每个块的奇异值生成12 bit认证水印，利用每个块的2×2子块均值的高5 bit生成恢复水印，将32 bit水印信息嵌入到相应的4×4映射块像素的最低两位中。杨彬彬等人(2015)提出了一种基于安全隐藏的图像分层篡改检测和内容恢复算法，该算法对图像进行4×4分块，对每个块基于DCT变换产生24 bit恢复水印，并用其2×2子块均值产生8 bit 认证水印，将认证水印嵌入在自身块中的最低2 bit中，将恢复水印嵌入到映射块的最低2 bit中。Lin等人(2005)提出了一种基于分块的多级认证脆弱水印算法，该算法对图像进行4×4分块，并用其2×2子块均值的高6 bit生成4×4该图像块的认证与恢复水印，选取其对应映射块的每个2×2子块生成2 bit的认证水印，达到对图像块的双认证目的。这类自嵌入水印算法嵌入水印后的图像失真较小。Al-Otum和Alansari(2019)提出了一种基于置乱的保持双水平矩方法的篡改检测和内容恢复图像水印方案，该算法将图像分为4×4块，基于双水平矩方法对每个块编码生成28 bit恢复水印，并依据每个块的均值生成4 bit认证水印，将其恢复和认证水印嵌入到映射块中。赵新辉和张晓培(2013)提出了一种结合DCT(discrete cosine transform)和矢量量化(vector quantization, VQ)编码的可恢复脆弱水印算法，该算法将图像分为8×8块，根据图像块的复杂度分别采用DCT编码或者VQ编码产生恢复水印，根据恢复水印产生认证水印，并将其嵌入在映射块中。Qian等人(2011)和Zhang等人(2011a)提出的算法都是对图像进行8×8分块，对每个块基于DCT变换生成水印。Zhang(2009)以及Zhang等人(2011b)的算法都是对图像进行8×8分块，分别依据每个块中像素高5 bit产生水印。Gul和Ozturk(2020)提出的算法是对图像进行16×16分块。这类算法认证粒度不细。

另一类是基于块截断编码的算法，Singh和Singh(2019)提出了一种基于块截断编码的具有恢复能力的图像认证有效水印方案，该算法将图像进行2×2分块，对每个块进行块截断编码生成恢复水印，依据恢复水印生成认证水印，将其嵌入到映射块最低3 bit中。Hemida和He(2020)提出了一种基于块截断编码和量子混沌映射的自恢复水印方案，该算法将图像分为4×4块，对每个块生成认证水印，并对其2×2子块基于块截断编码分为平滑块或者复杂块，生成相应的恢复水印，依据量子混沌映射生成块映射块嵌入水印。Chang等人(2020)提出了基于自适应权值压缩绝对块截断编码的脆弱水印图像恢复方案，该算法将图像分为4×4块，对其基于绝对块截断编码产生24 bit的认证与恢复水印，并将水印分别嵌入到两个不同的映射块中。Kim和Yang(2021)提出了一种基于绝对块截断编码和最优像素调整的自嵌入脆弱水印检测图像篡改的方案，该算法将图像分为4×4块，对其进行绝对块截断编码生成恢复水印，利用最优像素调整将恢复水印嵌入其相应映射块中，并依据每个块中像素生成认证水印，嵌入自身块中。

半脆弱水印研究主要应用了图像频域特性来实施水印的嵌入。Chen等人(2017)提出了一种抵抗JPEG压缩的半脆弱水印算法，该算法将图像分为8×8块，基于DCT变换生成认证与恢复水印，并将其嵌入到图像块的7个中频DCT系数中。Li等人(2015)提出了一种基于小波组量化和双重认证方法的可恢复的半脆弱水印算法，该算法将图像分为的16×16块，依据每个16×16块均值的高5 bit生成认证与恢复水印，对每个16×16的块进行小波变换产生第2份认证水印，并将生成的水印嵌入到映射块中。Rhayma等人(2019)提出了一种基于组合数据表示的半脆弱自恢复水印方案，该算法将图像分为32×32块，利用块的均值与其16×16子块的均值生成认证水印，对图像进行小波变换得到二阶低通系数，并基于组合数据表示方法对系数进行压缩得到恢复水印，将认证与恢复水印嵌入到映射块中。Egorova和Fedoseev(2020)提出了一种针对图像ROI(region of interest)并且对JPEG具有鲁棒性的图像内容恢复方案，该算法将图像分为8×8块，对ROI区域的块进行有损JPEG压缩后再编码生成认证和恢复水印，将水印嵌入到其他不感兴趣区域的块中。这类算法尽管能够抵抗对整幅图像的一些正常处理操作，但对图像认证的粒度不细。

篡改者为了达到某种目的，往往对图像的一些局部区域进行篡改，如人脸的重要部位、路牌信息、医学图像中的病灶等细节信息，并对修改区域及其边缘进行平滑处理操作，达到对抗图像检测的目的。本文提出了一种基于块截断编码的自嵌入半脆弱水印算法。算法首先利用块截断编码对图像4×4块的内容进行压缩编码；然后，对压缩信息进行哈希，并将压缩编码和哈希结果级联构成水印，嵌入到相应的映射块中。该算法通过以下两个策略提高嵌入水印后图像质量、认证粒度和对正常处理操作的鲁棒性： 1)基于2×2图像子块均值对4×4图像块内容进行块截断编码，压缩了图像的内容，缩短了水印的长度，保证了嵌入水印后图像的质量，提升了认证粒度； 2)基于对块截断编码量化值阈值的设置，保持了算法对图像平滑处理操作的鲁棒性和恶意篡改的敏感性。

1 算法描述

本文算法的基本思想是：在保证图像失真较小和细粒度认证精度条件下，水印能够对图像局部的平滑处理操作保持一定的鲁棒性。算法包括水印的生成、嵌入和认证恢复3个部分。其架构如图1所示。图1中，水印的生成部分将图像I分成4×4图像块Ii，并对任一图像块Ii进行2×2分块再编码产生16 bit 的编码信息Vi，利用密钥K1对Vi进行哈希处理得到16 bit的校验信息Ui，最终生成32 bit的水印信息Wi；水印的嵌入利用密钥K2找到Ii的映射块Iε(i)，ε(i)为映射块的索引标识。将水印Wi嵌入到Iε(i)中像素的最低2 bit中，得到含水印图像Iw；认证与恢复部分首先将目标图像I′分为4×4图像块I′i，对图像块I′i进行2×2分块编码得到V′i，提取图像块I′i和I′ε(i)中的最后2 bit信息得到W′δ和W′i′，利用V′i、W′i′、W′δ进行认证与恢复。

图1 算法框架图Fig.1 Algorithm framework

1.1 水印的生成

1)对于大小为M×N的原图像I，将其划分为n个不重叠的4×4块，并按行优先顺序排列，则原图像I表示为

I={Ii|i=1,2…,n}

(1)

(2)

(3)

(4)

(5)

(6)

Vi=F(bi,Hi,Li)

(7)

4)利用密钥K1对编码信息Vi进行哈希计算，得到16 bit的校验信息Ui,即

Ui=Hash(K1,Vi)

(8)

5)将Vi和Ui级联构成块Ii的32 bit的水印信息Wi,即

Wi=(Vi,Ui)

(9)

1.2 水印的嵌入

1)利用密钥K2生成图像块Ii的映射块Iε(i)，其中ε(i)需满足以下条件

ε(i)=[(K2×i)modn]+1

(10)

式中，i∈[0,n]，ε(i)∈[0,n]，K2∈[1,n-1]，n为图像中4×4块的总个数。

2)将Ii的32 bit水印信息Wi替换到Iε(i)的像素最低2 bit，得到含水印图像Iw。

1.3 认证与恢复

认证阶段包含以下主要步骤：

1)对待认证图像I′进行4×4分块，对每个4×4块进行2×2分块

I′={I′i|i=1,2,…,n}

(11)

2)利用水印生成步骤生成块I′i的水印V′i,即

V′i=F(b′i,H′i,L′i)

(12)

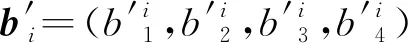
3)利用密钥K2找到I′i的映射块I′ε(i)，提取块I′ε(i)中像素最低2 bit，记做w′i′,即

w′i′=(V′i′,U′i′)

(13)

式中，(b′i′,H′i′,L′i′)=F-1((V′i′)，b′i′=(b′1′i,b′2′i,b′3′i,b′4′i)。

4)提取块I′i中像素最后2 bit，得到32 bit信息，记做W′δ,即

W′δ=(V′δ,U′δ)

(14)

式中，i=[(K2×δ)modn]+1。

5)对图像块I′i而言，若U′δ=Hash(K1,V′δ)，则表明嵌入在I′i块的水印未被篡改，视做块I′i通过认证。

6)对图像块I′i而言，若U′δ≠Hash(K1,V′δ)，但U′i′=Hash(K1,V′i′)，则表明嵌入在I′i块的水印被篡改，视做I′i被篡改，而I′i块的水印w′i′在映射块I′ε(i)中未被篡改，则

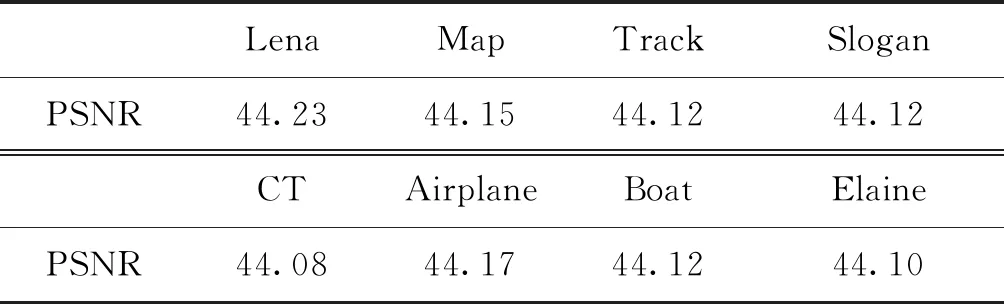
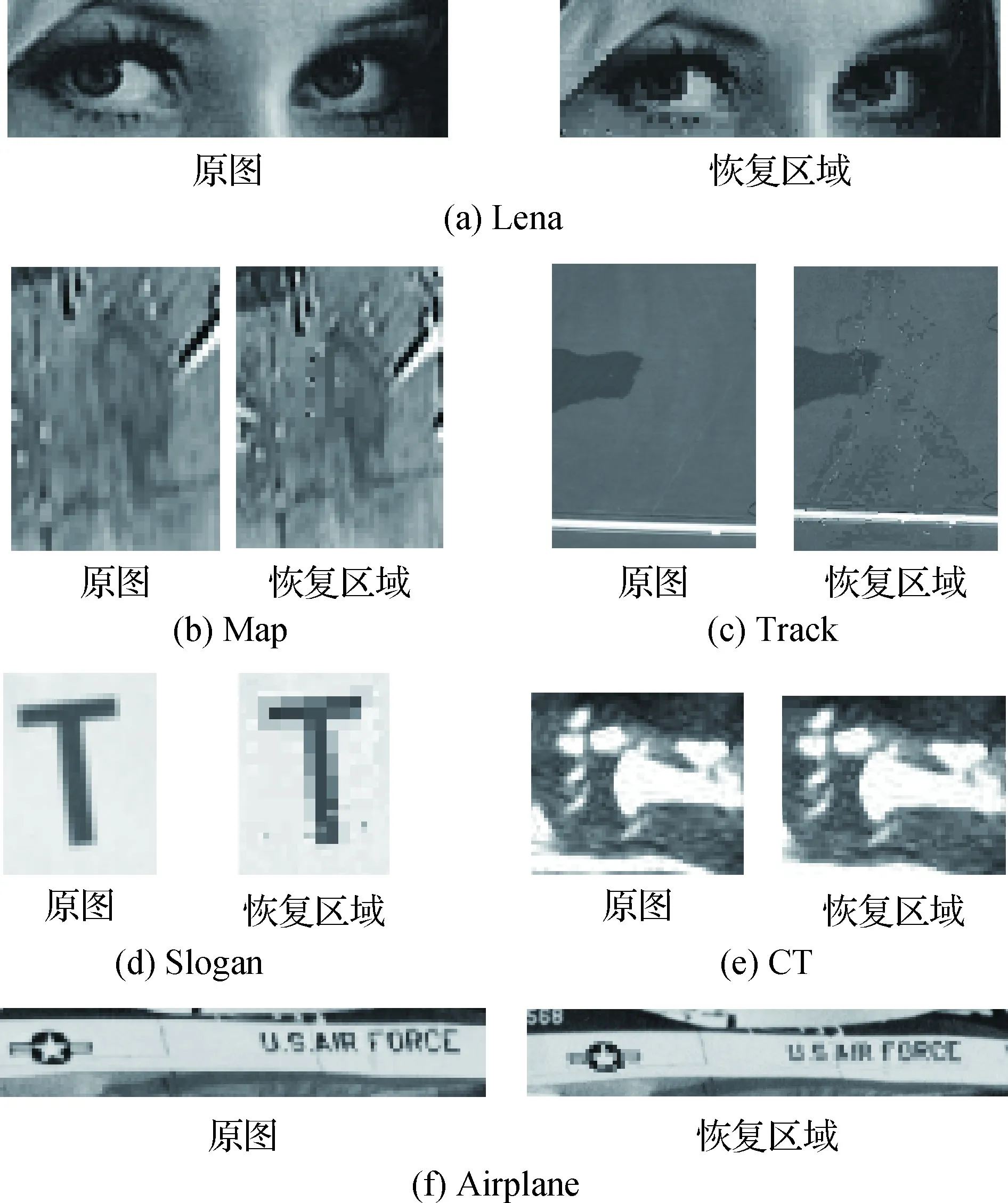
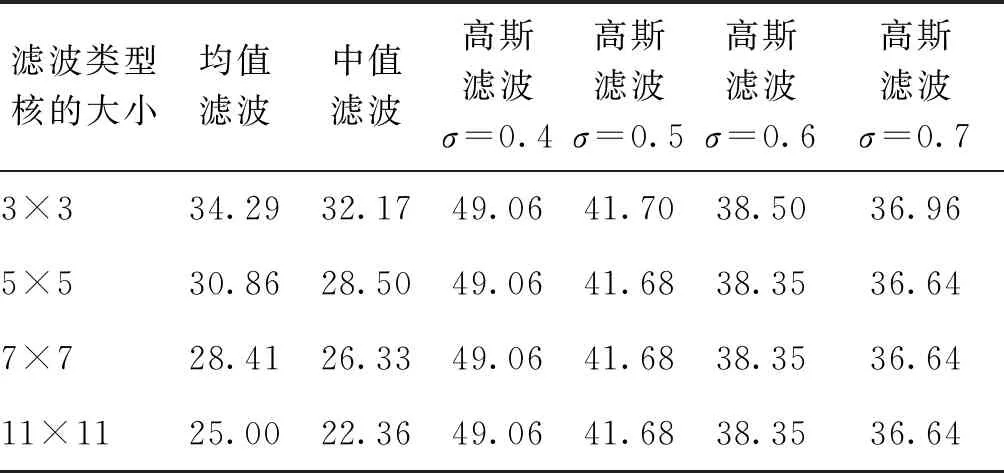
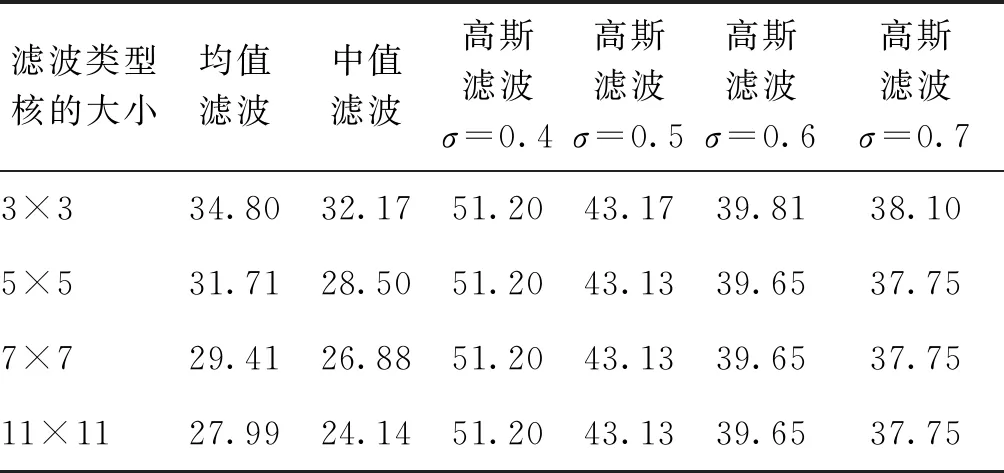
(1)若b′ji=b′j′i=1，且|H′i-H′i′|

(2)若b′ji=b′j′i=0，且|L′i-L′i′|

(3)否则图像子块I′i,j不通过认证。

其中，d为正常图像操作的可容忍修改阈值。

篡改恢复阶段包含以下主要步骤：

1)若图像块I′i不通过认证，且U′i′=Hash(K1,V′i′)，则表明I′i块生成的水印未被篡改，若图像子块I′i,j未通过认证，则对图像子块I′i,j进行恢复,即

(15)

2)若图像块I′i不通过认证，且U′i′≠Hash(K1,V′i′)，则表明I′i块生成的水印被篡改，无法利用水印w′i′对I′i,j进行恢复，则利用块I′i,j周围的8×8邻域子块的均值来恢复I′i,j。

3)最终得到恢复图像Ir。

2 实验结果与分析

本文实验分为实验性能测试和与其他方法比较测试两部分，采用BOWS2(Break Our Watermarking System 2nd)(http://bows2.ec-lille.fr/)比赛使用的图像库，图像库中包含10 000幅不同场景(风景、人物、建筑和图标等)的512×512像素的灰度图像，图像库中的100幅图像作为实验对象。并另选取其他8幅典型场景下的图像展示算法的篡改认证和恢复性能(如图2所示)。

图2 测试图像Fig.2 Test image((a)Lena; (b)Map; (c)Track; (d)Slogan; (e)CT; (f)Airplane; (g)Boat; (h)Elaine)

2.1 本文算法的性能实验

2.1.1 嵌入水印后的图像质量

图3给出了使用本文算法嵌入水印后的水印图像，表1给出了各嵌入水印后图像相对于原始图像的峰值信噪比(peak signal-to-noise ratio, PSNR)值。从表1中可以看出，测试图像的PSNR都达到了44 dB以上，表明含水印图像具有较高的视觉质量。

图3 嵌入水印后的图像Fig.3 Watermarked images((a)Lena; (b)Map; (c)Track; (d)Slogan; (e)CT; (f)Airplane; (g)Boat; (h)Elaine)

表1 嵌入水印后图像相对于原始图像的PSNR

2.1.2 对图像篡改的认证与恢复实验

利用本文算法对图Lena、Map、Track、Slogan、CT、Airplane的含水印图像篡改的认证与恢复结果，如图4—图7所示。

图4 篡改图像Fig.4 Tampered images((a)Lena; (b)Map; (c)Track; (d)Slogan; (e)CT; (f)Airplane)

图4显示了对图3中的前6幅(a)—(f)的不同局部区域的篡改结果。对图3(a)中人物的眼睛、图3(b)中地图中的飞机、图3(c)中的场景、图3(d)中的路标、图3(e)中的肿瘤病灶、图3(f)中的飞机标志进行篡改，篡改率分别为1.13%、0.05%、4.2%、1%、0.01%、0.8%。其篡改区域认证结果如图5所示，恢复结果如图6所示，图3(a)—(f)的恢复后图像相对于含水印图像的PSNR分别为42.8 dB、43.3 dB、41.8 dB、42.1 dB、44.0 dB、40.7 dB。

图5 认证结果Fig.5 Identified images((a)Lena; (b)Map; (c)Track; (d)Slogan; (e)CT; (f)Airplane)

图6 恢复结果Fig.6 Restored images((a)Lena; (b)Map; (c)Track; (d)Slogan; (e)CT; (f)Airplane)

图7 原图与恢复区域的对比图Fig.7 Comparison charts of original images and restored areas((a)Lena; (b)Map; (c)Track; (d)Slogan; (e)CT; (f)Airplane)

2.1.3 对图像大区域篡改的认证与恢复结果

图8给出了对水印图像(图3(g))进行剪切篡改，篡改率为50%时的认证与恢复结果，恢复图像相对于含水印图像的PSNR为30.1 dB。

图8 图3(g)水印图像的篡改、认证与恢复结果Fig.8 Tampered, identified and restored results of watermarked image Fig.3 (g)((a)watermarked image；(b)tampered image;(c)identified image;(d)restored image)

表2给出了6幅测试图像Lena、Map、Track、Slogan、CT、Airplane分别在篡改率5%、10%、20%、30%、40%、50%下的恢复图像相对于含水印图像的PSNR。随着篡改率的增大，恢复后图像的质量下降。即使在篡改率达到50%时，图像的恢复质量仍超过28.6 dB，表明本文算法能够对大面积篡改实现有效恢复。

表2 不同篡改率下的恢复图像相对于含水印图像的PSNRTable 2 PSNR of the recovered content relative to watermarked image with different tampering rates /dB

为进一步测试算法的恢复能力，针对BOWS2图像库中选取的100幅测试图像，分别进行了算法运行时间的统计、含水印图像相对于原始图像PSNR统计和不同篡改率下恢复图像的PSNR统计。算法对100幅图像生成和嵌入水印所用时间约为315.12 s，平均一幅图像所用时间约为3.15 s。100幅图像嵌入水印后相对于原始图像的平均PSNR为44.12 dB。

表3给出了100幅图像在不同篡改率下恢复图像相对于含水印图像的平均PSNR和恢复所用的平均时间。从表3中可以看出，恢复图像相对于含水印图像的平均PSNR随着篡改率的增大而减小，认证和恢复的运行平均时间基本保持在3.6 s以内。

表3 针对100幅图像在不同篡改率下恢复图像相对于含水印图像的平均PSNR和恢复所用的平均时间Table 3 The average PSNR relative to the watermarked image and the average time taken to restore the image for 100 images at different tampering rates

2.2 算法对局部区域平滑滤波的抵抗能力

以图3(h)为例，在算法中d取4的情况下，对其局部区域(滤波区域为80×80，共1 600个2×2的块)分别进行高斯、均值和中值滤波操作，测试水印抵抗局部滤波操作的能力，其结果如图9—图11所示。

图9 针对图3(h)在滤波核为3×3、5×5、7×7，σ为0.40.6的高斯滤波处理后的认证结果Fig.9 Fig.3(h) authentication result after the Gaussian filter with filter core of 3×3, 5×5, 7×7， and σ of 0.40.6((a) filter core of 3×3,σ=0.4；(b) filter core of 3×3,σ=0.5； (c) filter core of 3×3,σ=0.6；(d) filter core of 5×5,σ=0.4； (e) filter core of 5×5,σ=0.5； (f) filter core of 5×5,σ=0.6；(g) filter core of 7×7,σ=0.4；(h) filter core of 7×7 σ=0.5；(i) filter core of 7×7,σ=0.6)

图10 针对图3(h)在滤波核为3×3、5×5、7×7的均值滤波处理后的认证结果Fig.10 Fig.3(h) authentication results under the mean filter processed with the filter core of 3×3，5×5，7×7 ((a) filter core of 3×3；(b) filter core of 5×5；(c) filter core of 7×7)

从图9—图11的结果看出算法在对局部区域平滑滤波是有一定的抵抗能力的。图9可以看出算法对高斯滤波的鲁棒性和滤波核的大小无关，但是随着σ的增大鲁棒性减弱。图10和图11可以看出算法对均值滤波和中值滤波的鲁棒性随着滤波核的增大而减弱。

图12显示了图3(h)在均值、中值、高斯滤波操作下的认证图像中未通过认证块的数量，可以看出只有少量2×2图像块未通过认证，高斯滤波操作下未通过认证块的数量最少。且未通过认证块的数量随着均值滤波核和中值滤波核的增大而增加，随着高斯滤波的σ增大而增加。图12验证了算法对均值滤波、中值滤波和高斯滤波具有鲁棒性，且对高斯滤波的鲁棒性最强。

图13显示了100幅图像在均值、中值、高斯滤波操作下，认证图像中未通过认证块数量的平均值，可以看出实验结果与图12结果基本一致，平均未通过认证块的数量随着均值滤波核和中值滤波核的增大而增加，随着高斯滤波的σ增大而增加。

图11 针对图3(h)在滤波核为3×3、5×5、7×7的中值滤波处理后的认证结果Fig.11 Fig.3(h) authentication result under the median filter processed with the filter core of 3×3，5×5，7×7((a) filter core of 3×3；(b) filter core of 5×5；(c) filter core of 7×7)

图12 针对图3(h)在均值、中值、高斯滤波处理后的认证情况Fig.12 Fig.3(h) authentication results after mean, median, and Gaussian filter processed

图13 针对100幅图像在均值、中值、高斯滤波处理后的认证情况Fig.13 Authentication results of 100 images after mean, median, and Gaussian filter processed

2.3 算法中阈值d的取值对滤波操作鲁棒性的影响

表4给出了图3(h)分别在不同滤波操作下图像滤波区域图像块的PSNR。其中均值滤波和中值滤波在滤波核为11×11时，滤波区域的PSNR分别为25.00 dB和22.36 dB，近似于恶意篡改，滤波后的图像如图15所示。表5给出了100幅图像分别在不同滤波操作下图像滤波区域图像块的平均PSNR，可以看出不同图像在经过滤波核为11×11的均值和中值滤波操作后，滤波区域的平均PSNR分别为27.99 dB和24.14 dB，都近似于恶意篡改。从图14可以看出，d在选取合适值时，图像在滤波核为11×11的均值和中值滤波操作后的认证图像中大量的2×2图像块仍能通过认证。

2.4 实验对比

本节给出了本文算法与对比算法(Qian等，2011；Zhang等，2011a，b；Zhang和Wang，2009；Singh和Singh，2019；Chang等，2020；Gul和Ozturk，2020；Kim和Yang，2021)的性能比较，结果如表6所示。

Qian等人(2011)算法对于篡改率小于35%的图像恢复质量最高可为35.0 dB；Zhang和Wang(2009)算法对于篡改率小于6.6%的图像恢复质量最高可为37.9 dB；Kim和Yang(2021)算法对于篡改率在5%和45%时的图像恢复质量分别为40.0 dB和36.6 dB，这3种算法在篡改率为50%时无法恢复图像。而本文算法可在篡改率5%和50%时进行图像恢复，图像恢复质量分别为32.7 dB和41.8 dB， Singh和Singh(2019)的算法以及Chang等人(2020)算法的恢复条件与本文算法一样，在篡改率为5%时图像恢复质量分别为28.7 dB和39.1 dB，在篡改率为50%时图像恢复质量分别为29.3 dB和41.3 dB，相较而言本文算法的恢复效果较好。而Zhang等人(2011a)算法、Zhang等人(2011b)算法以及Gul和Ozturk(2020)算法的恢复条件比本文算法更好，最高可接受篡改率分别为60%、54%和75%，但是本文方案在水印图像的质量方面更具优势，水印图像的质量为44.23 dB， Zhang等人(2011a)算法、Zhang等人(2011b)算法以及Gul和Ozturk(2020)算法的水印图像质量分别为37.9 dB、37.9 dB和44.14 dB。算法的时间复杂度方面，Gul和Ozturk(2020)算法的时间复杂度为O((n/16)2)， Singh和Singh(2019)算法的时间复杂度为O((n/2)2)，Qian等人(2011)的算法、Zhang等人(2011a，b)的算法以及Zhang和Wang(2009)的算法的时间复杂度为O((n/8)2)，而Chang等人(2020)算法和本文算法的时间复杂度为O((n/4)2)。

图14 针对100幅图像在恶意篡改和不同滤波处理后的认证结果Fig.14 Authentication results of 100 images after mean, median, and Gaussian filter processed

表4 针对图3(h)在不同滤波处理后改变区域的PSNRTable 4 PSNR of Fig.3 (h) changed area after different filters processed /dB

图15 针对图3(h)分别在滤波核为11×11的均值和中值滤波处理后的图像Fig.15 Fig.3(h) after the mean and median filter processed with the filter core of 11×11((a) mean filter, core of 11×11；(b) median filter, core of 11×11)

表5 针对100幅图像在不同滤波处理后改变区域的平均PSNRTable 5 Average PSNR of 100 images changed area after different filters processed/dB

表6 本文方案与几种水印方案的性能比较Table 6 Comparison between the proposed scheme and several watermarking schemes

综上可以看出，本文算法与对比算法(Qian等，2011；Zhang等，2011a，b；Zhang和Wang，2009；Singh和Singh，2019；Chang等，2020；Gul和Ozturk，2020；Kim和Yang，2021)相比在水印图像视觉质量、篡改认证恢复等方面各具优势，相关性能方面甚至高于这些算法。

3 结 论

本文提出了一种基于块截断编码的自嵌入半脆弱水印算法。算法利用块截断编码对图像内容进行压缩，有效降低了水印的长度，提升了图像的视觉质量；基于对块截断编码量化值阈值的设置，保持了算法对图像平滑处理操作的鲁棒性和恶意篡改的敏感性。本文算法在对图像局部的平滑滤波处理具有鲁棒性的同时保持了算法的认证粒度，认证粒度为2×2，而现有的半脆弱水印算法的认证粒度一般为8×8级的，甚至有些算法的认证粒度为16×16级。本文算法在认证粒度上更具优势。

本文算法考虑到图像的篡改往往是区域性的，所以按一定规则的方式来嵌入水印，但不适用于随机篡改。在今后的工作中要设计不同的嵌入方式来应对不同方式的篡改。