3D网格隐写与隐写分析回顾与展望

周航，陈可江，张卫明*，俞能海

1. 中国科学技术大学信息科学技术学院， 合肥 230027； 2. 西蒙弗雷泽大学计算机科学学院， 加拿大 温哥华 V5A1S6； 3. 中国科学院电磁空间信息重点实验室， 合肥 230027

0 引 言

隐写术是一类信息隐藏方法，其主要目标是将秘密消息隐藏在某个数字载体之中并传送给接收方，而不引起第三方的注意，是隐蔽通信或隐蔽存储的一种重要形式(Pevny和Fridrich，2008)。与传统加密技术将明文转换为密文后传输密文不同，隐写利用数字媒体的冗余性，修改局部载体以隐藏秘密消息。数字隐写术作为信息隐藏中的重要技术，自20世纪90年代末以来，持续受到国防安全部门和学术界的重视。隐写术的发展为隐蔽通信带来了便利，但同时也给犯罪组织提供了从事非法活动的手段。有新闻报道，一些著名网站，如eBay和Amazon等已经成为恐怖分子传播秘密信息的隐蔽渠道。已有国际恐怖组织将欧美一些科学家早期关于隐写的研究应用于实践。随着隐写技术的发展，新的隐写理论和隐写算法不断涌现，网络上更是出现了很多可以免费下载使用的隐写工具。因此，为了避免隐写技术被不正当利用所带来的危害，隐写分析技术的研究也在不断地推进，这也给数字隐写的设计带来了更大的挑战。

传统隐写主要的研究载体是图像、视频和音频等常见的多媒体数据，而本文关注的是随着虚拟现实、实时仿真和交互式3维设计技术发展产生的3D模型的隐写技术。这类3D模型作为许多重要应用的底层支撑技术，是计算机图形学的一个基础性研究课题。早期计算机图形学旨在解决如何在计算机中表示3维几何图形，以及如何利用计算机进行图形的生成、处理和显示的相关原理与算法，产生令人赏心悦目的真实感图像。经过40年的发展，广义的计算机图形学的研究非常广泛，如图形交互技术、光栅图形生成算法、曲线曲面造型、实体造型、真实感图形计算与显示算法，以及计算机动画、自然景物仿真和虚拟现实等。随着计算机图形学的发展和大数据时代计算性能的提高，3D模型的隐写和隐写分析的研究也与日俱增，近几年得到了重视。2D图像隐写通过修改像素值的方式嵌入秘密消息，与之不同的是，3D网格隐写通过修改顶点坐标或顶点存储顺序嵌入消息。相比于像素调制，顶点坐标调制在x,y,z这3个坐标分量上均可实现调制，因此在设计3D网格隐写算法时相比于图像隐写更为复杂。

研究3D模型的隐写技术满足了复杂多样的社交环境下多媒体数据隐写安全性的迫切需求，对于创造更为安全的隐蔽通信手段也有重要的影响。首先，复杂多样社交环境下的隐写技术研究有助于保障信息通信的安全性。面对复杂多样的隐写分析者，如何进一步提升隐写的安全性，从而创造更为安全的隐蔽通信手段则成为当前隐写技术研究的重要内容。其次，大数据环境下亟需新型载体隐写技术。随着网络和多媒体技术的发展，当前涌现了大量新型多媒体。作为合适的隐蔽通信载体，新型多媒体隐写技术的研究也随之展开。

本文对现有的3D网格隐写和隐写分析方法进行了较为全面的总结和分析。根据消息嵌入的位置将3D网格隐写算法分为两态调制隐写、最低有效位(least significant bit, LSB)隐写、置换隐写和变换域隐写4类，以及将3D网格隐写分析算法分为通用型隐写分析和专用型隐写分析2类。为更好地描述与分析，首先简要介绍隐蔽通信基本模型；然后评估隐写算法安全性的数据集及评价指标；接着，分别介绍每类3D网格隐写算法和隐写分析算法的基本思想、代表性改进方案以及优缺点总结等，并对典型方法在数据集上总结和分析性能；最后，对3D网格隐写和隐写分析方法的未来发展方向进行了初步展望。

1 隐蔽通信基本模型

现代的隐写模型都是基于囚犯问题(Simmons，1984)设计的，该问题中Alice与Bob需要在Wendy的监视下实现隐蔽通信。通过图1所示的隐写系统可以达到该目的，其中Alice享有密钥k1，Bob享有密钥k2，c是一个被Wendy认可的载体。一般情况下，在私钥隐写系统中，k1=k2。隐写过程如下：Alice将待传递消息m使用密钥k1加密后，通过隐写嵌入步骤Emb(·)将其嵌入载体c得到载密s，然后在Wendy监视下的信道中将s传输给Bob，即

Emb(c,m,k1)=s

(1)

Bob接收到s后利用提取步骤Ext(·)和密钥k2得到消息m，完成一次隐蔽通信

Ext(s,k2)=m

(2)

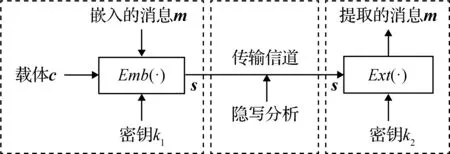
图1 数字隐蔽通信和隐写分析示意图Fig.1 Diagram of digital covert communication and steganalysis

2 数据库及评价指标介绍

3D网格是多边形小平面的集合，是真实3D物体的适当近似。随着3维表面重建和密集即时定位与地图构建(simultaneous localization and mapping，SLAM)的兴起，利用点云—网格生成算法，对海量的3维点云数据预处理得到3D网格。通常，根据不同的拓扑需求和算法需求，会选择不同的3D网格数据结构。最常见的数据结构为面数据结构，由网格所有面的集合构成，而对于每一个面则使用组成面多边形的点来表示。3D网格包含3种不同的组成元素：顶点、边和面。3D网格也可由几何信息和连接信息描述，其中几何信息描述了顶点的3D位置(坐标)，连接信息提供了邻接关系。

3D网格通常按一定的顺序排列顶点和面。尽管面列表包含冗余信息，但能够加速网格上的几何和拓扑运算。面通常由三角形(对应于三角形网格)、四边形(对应于四边形网格)或其他简单的凸多边形(对应于多边形网格)组成。由于三角形网格是当前主流3D网格，因此，本文仅考虑三角形网格。

2.1 数据库

普林斯顿分割集(Princeton segmentation benchmark)包含354个网格(Chen等，2009)，主要用于3D网格分割任务。其中，260对载体—载密网格对用于训练分类器，剩余94对作为测试样本。

普林斯顿网格(Princeton ModelNet)包含12 311个40类网格数据。其中，50%的网格用于分类器训练，剩余网格作为测试样本。

2.2 评价指标

2.2.1 隐写评价指标

安全性、容量和鲁棒性用于评估隐写算法性能。

1)安全性。如果秘密消息的存在只能以不高于随机猜测的概率来估计，则隐写算法可以被认为在隐写分析系统中是完全安全的。

2)容量。为了实现传达秘密消息的高效性，隐写术提供的隐藏能力应尽可能高，可通过相对有效载荷(也称为嵌入率)，即比特每顶点(bit per vertex，bpv)评估。

3)鲁棒性。尽管大多数隐写方法并不追求鲁棒性，但在实际应用中，由于网络流量、带宽和智能设备处理能力的限制，通信信道是有损耗的，导致传输媒体的性能下降，并进一步影响秘密消息的正确提取，因此，有时候有必要考虑隐写算法的鲁棒性。

2.2.2 隐写分析评价指标与典型的分类器

隐写分析的主要目的是确定载体是否嵌入了秘密消息。如果使用某种隐写分析方法来检测可疑的载体，则会有4种可能的结果：

1)真阳性(TP)：载密被正确分类为载密;

2)假阴性(FN)：载体被错误分类为载密;

3)真阴性(TN)：载体被正确分类为载体;

4)假阳性(FP)：载密被错误分类为载体。

载体和载密数据混合而成的隐写分析结果可以构成2×2混淆矩阵，评估指标包括

(3)

(4)

(5)

(6)

式中，R为召回率，FPO为假正率，ACC为准确率，PR为查准率。

支持向量机(support vector machine，SVM)是一种监督式机器学习模型，用于解决分类问题。然而，随着特征空间维数和训练样本的增加，SVM的复杂度和内存需求也迅速增加。为了能够处理高维特征，在实验中一般使用集成分类器分类。

(7)

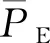
3 3D网格隐写

根据秘密消息嵌入方式，3D网格隐写算法可分为4类：两态调制隐写、最低位隐写、置换隐写和变换域隐写。在3D网格信息隐藏的早期研究阶段，研究人员将水印和隐写术视为相同的技术，并提出了一批嵌入秘密信息的算法。

以下为几种典型数字攻击(Zhou等，2021b)：

1)仿射变换(包括平移、旋转和缩放)。通过移动3D网格或者相机拍摄位置得到变换矩阵，也可通过齐次变换矩阵表示变换过程。

2)顶点重新排序。重新排序不会改变网格拓扑结构，只改变存储顶点的布局，并赋予新的索引。

3)加噪。扫描得到的3D模型通常是带噪模型，由扫描设备和数字化过程产生。

4)平滑。过滤掉高频信号。

5)简化。降低网格处理的复杂度。

3.1 两态调制隐写

两态调制隐写等分邻近两个坐标点之间的线段，标记为01两个状态。根据秘密消息的值对应的状态来相应地修改第3个点的坐标。

早期的3D网格隐写算法常采用两态调制隐写作为基础算法。Cayre和Macq(2003)提出采用量化索引调制技术来调制某个三角面片顶点的坐标值，以嵌入消息0或1。Wang和Cheng(2005)提出基于层级k-维树和高级跳跃策略的快速路径搜索方法，并提出在嵌入区域的多层分段嵌入消息以实现更高的容量。Wang和Wang(2006)提出抗置换攻击的嵌入算法，将坐标点变换到由主成分分析构建的空间，并通过相邻点之间的坐标调制嵌入消息。Chao等人(2009)提出了大容量的可逆隐写方法，首先旋转和放缩3D模型，校准至主成分分析变换得到的主轴、次轴和垂直主轴与次轴的方向上，然后将每个轴上的点根据坐标位置等间隔划分并聚类，最后通过空间调制嵌入消息。Itier和Puech(2017)提出了基于静态算术编码和哈密顿图的嵌入方法，但是嵌入产生的修改幅度较大。由于通过此方法得到的载密网格在球坐标系下的方位角和仰角坐标分量有较为明显的修改，容易受到隐写分析的检测，因此，为了抵抗隐写分析，Li等人(2017a)提出仅在距离分量上嵌入消息。

以上两态调制隐写算法中，Chao等人(2009)算法隐写的容量相对较大，Li等人(2017a)的隐写算法具有较明显的抗隐写分析检测性能。这类方法基于统计位移嵌入消息，对加性噪声攻击、拉普拉斯平滑攻击和网格简化攻击具有鲁棒性。值得一提的是，已经有一些隐写分析方法能够检测某些隐写算法。此外，嵌入过程中的优化算法阻碍了水印嵌入的速度。由于顶点数量有限，因此嵌入容量仍然很小。此外，由于修改幅度明显，因此这类方法无法抵御隐写分析。

3.2 最低位隐写

最低位隐写首先将消息编码至最低有效位平面，并随着嵌入量向更高位平面嵌入信息。

Yang等人(2013)提出了估计坐标点曲率，并依据曲率大小自适应修改部分坐标点的最低位以嵌入消息的3D网格隐写方法。Li等人(2017b)提出了在失真约束下基于密钥调制的3D网格隐写算法。Zhou等人(2019)提出了基于自适应于顶点复杂度的网格顶点的失真函数，并采用校验栅格编码(syndrome trellis code, STC)(Filler等，2011)嵌入秘密消息，实现更高安全性的隐写性能。

最低位隐写算法通常为大容量抗检测算法，其性能由相同嵌入率下的抗检测性能评估。以上最低位隐写算法中，Zhou等人(2019)提出的隐写算法具备最强的抗检测性能。这类算法无法抵御加性噪声攻击、拉普拉斯平滑攻击和网格简化攻击，但对隐写分析有一定的抗检测性。

3.3 置换隐写

置换隐写基础原理是通过秘密消息的值扰动坐标或拓扑结构集合中元素的顺序实现消息嵌入。由于3D网格包含具有可重排顶点和三角面的集合，这为置换隐写提供了消息嵌入的空间。每种元素的排列顺序可以单一地映射为某个整数，因此，通过更改集合中元素的顺序可嵌入秘密消息。

然而，当载体元素较多时，使用置换隐写算法的计算复杂度很高，因此，研究者们通过权衡嵌入容量和时间复杂度以降低置换隐写算法的复杂度。Bogomjakov等人(2008)提出了改进的置换隐写算法，通过秘密消息分段编码排列值，并扰动排列值对应位置的坐标元素以嵌入消息。Huang等人(2009)改进了编码方式，在相同的嵌入效率下提升了嵌入容量。Tu等人(2010a)、Tu和Tai(2012)分别提出了基于二叉树、左斜二叉树和最大期望树的编码方法，进一步提升了嵌入容量。由于置换隐写会导致存储结构上相邻坐标点的邻域相关性下降，容易受到针对性隐写分析的检测，因此，Wang等人(2019)提出在坐标点的一环近邻域编码嵌入消息以抵抗检测。置换隐写的嵌入容量与载体长度相关，当载体顶点数达到5 000时，最大的嵌入率能够达到11 bpv。

以上置换隐写算法中，Tu和Tai(2012)的算法隐写容量相比较而言最大，Wang等人(2019)的隐写算法具有一定的抗隐写分析检测性能。这类算法具有较大的秘密信息嵌入容量，而且对基于坐标修改的攻击(仿射变换攻击、加噪攻击和平滑攻击)具有完全的鲁棒性。

3.4 变换域隐写

变换域隐写算法基础原理是预先经过某种映射变换顶点坐标值，然后在变换域中嵌入秘密消息。

Cho等人(2007)提出了在球坐标系下将顶点坐标与球心坐标的距离作为度量值，分段聚类后均值调制嵌入秘密消息的算法。Bors和Luo(2013)改进了此方法，增加了表面平滑性的约束。Kanai等人(1998)提出基于小波变换域和多分辨率表征下的秘密消息嵌入算法。变换域隐写算法具有鲁棒性强和嵌入容量低的特点。

变换域隐写算法主要评价其鲁棒性。Cho等人(2007)以及Bors和Luo(2013)提出的方法均具有较强的抗攻击性能。这类算法由于嵌入位置与坐标无关，因此对绝大多数攻击算法均具备一定的鲁棒性，但其主要缺点为低嵌入容量。

3.5 算法比较

本节比较了不同的隐写方法的性能。表1比较了不同隐写算法的失真和安全性。若某一隐写算法能有效抵抗所有隐写分析的检测，则视该隐写算法是安全的；否则不安全。对嵌入容量没有进行具体比较，是因为不同隐写算法对于容量上下限的评估不同。对于两态调制隐写和最低位隐写，大多数方法都有严格的容量上限，即不能嵌入超过上限的消息量。而置换隐写方法的上限是估计值，可以逼近但达不到，因此上限不是紧致的。表2是不同隐写算法鲁棒性的比较，其中数字攻击包括仿射变换、顶点重新排序、加噪、平滑和简化攻击等。

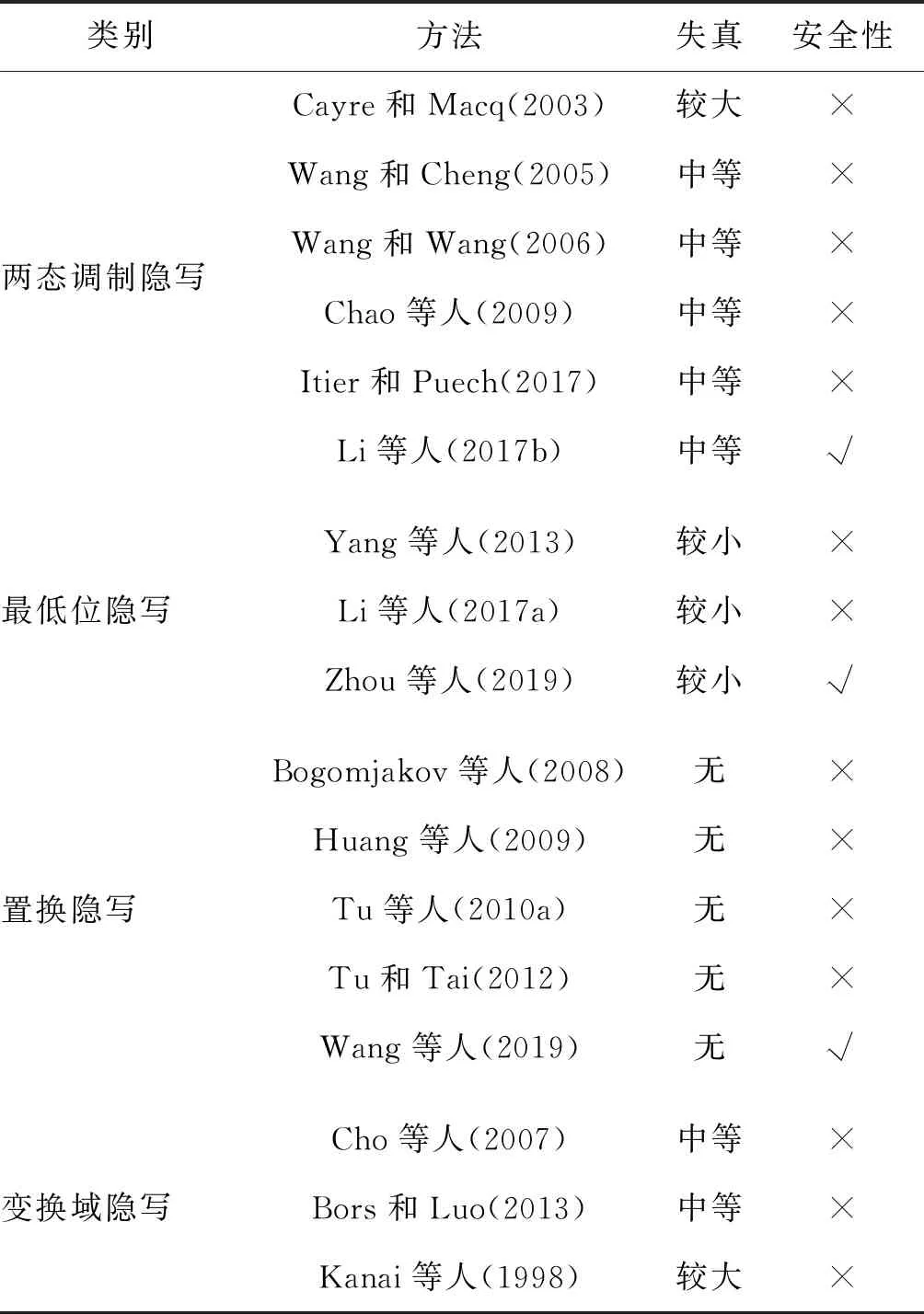
表1 3D网格隐写算法失真和容量的比较Table 1 Comparison of steganographic methods in terms of distortion and security

4 3D网格隐写分析

3D网格隐写分析与图像隐写分析相似，均通过提取邻域元素之间的相关性特征作为分类的依据。两者的不同在于图像像素的相关性通常在图像卷积基础上计算得到，而3D网格坐标邻域相关性通常由网格卷积作为预处理步骤。如前所述，3D网格相邻元素之间具有强相关性，即邻域残差的直方图呈现较陡的状态。由于隐写算法会破坏相邻元素之间的相关性，并造成载密3D网格邻域元素相关性下降，因此目前的隐写分析方面的研究主要集中于通过分析3维空间中相邻元素间的关联度设计残差特征，并进一步训练隐写分析分类器实现二分类。3D隐写分析可分为通用型隐写分析和专用型隐写分析。通用型隐写分析主要检测基于坐标点修改的隐写算法，包括两态调制隐写、最低位隐写和变换域隐写算法的检测。

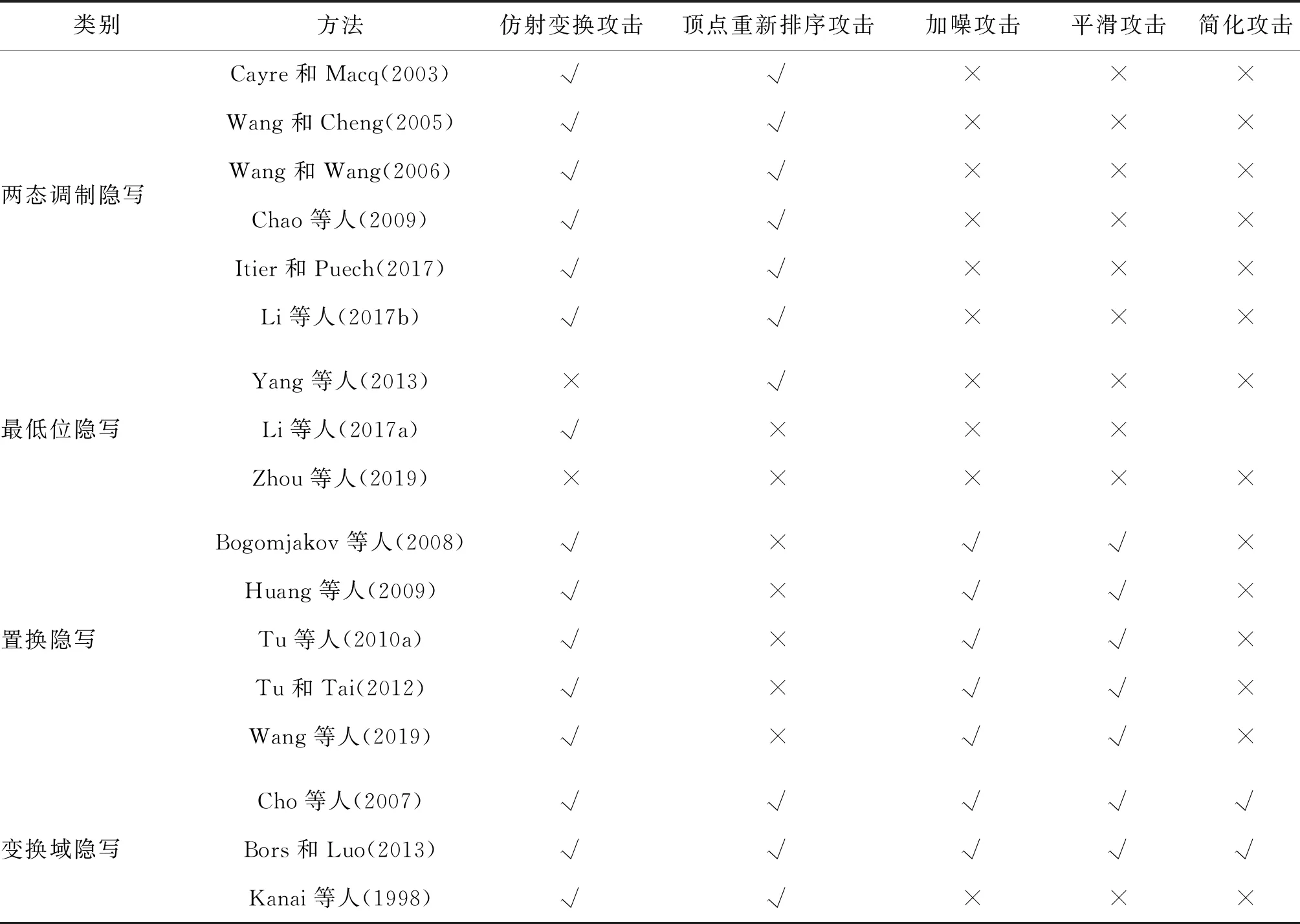
表2 3D网格隐写算法鲁棒性比较Table 2 Comparison of steganographic methods in terms of robustness

4.1 通用型隐写分析

通用型隐写分析由标准化(基于主成分分析(principal component analysis, PCA)的旋转和缩放)、特征提取和分类器的训练构成，如图2所示。其中，3D网格特征由原始3D网格特征与一环邻域均匀拉普拉斯平滑后的3D网格特征的距离表示。在特征提取之前，顶点坐标需要归一化：将3D网格原先的坐标旋转至主成分分析获得的3个主轴方向，并缩放至单位立方体内。

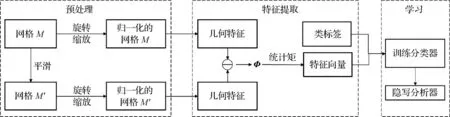
图2 基于统计残差特征学习的3D网格隐写分析框架图Fig.2 3D mesh steganalysis framework based on learning from statistics of residual features and classification

受图像隐写分析启发，载密图像与其平滑后的图像之间的差异大于载体图像与其平滑后的图像之间的差异(Fridrich等，2002；Kodovsky和Fridrich，2009)。由于隐写过程对3D网格也造成了同样的影响，因此，3D网格的隐写分析也遵循同样的原则，分别对原始信号和平滑后信号计算残差特征，即图2中“⊖”，并且计算统计矩进行降低处理。表3根据隐写分析特征设计角度比较了不同隐写分析特征和特征维数。

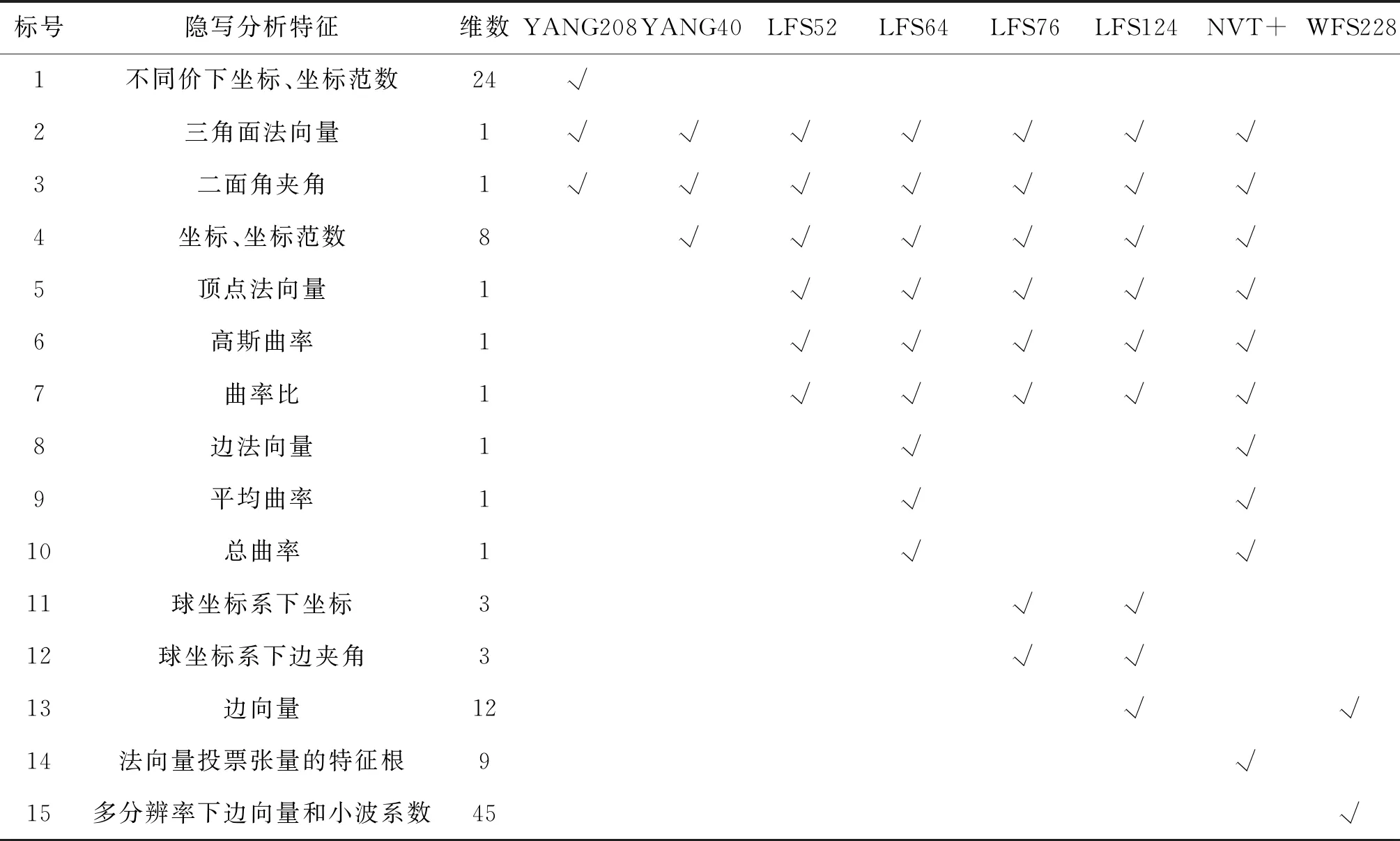
表3 3D网格隐写分析方法的基本特征元素Table 3 Basic feature elements of all 3D mesh steganalytic methods

4.1.1 Yang208特征

Yang和Ivrissimtzis(2014)首次提出了检测载体载密3D网格的隐写分析特征，包括基于笛卡儿坐标系下和拉普拉斯坐标系下的坐标分量变化、坐标向量长度变化和坐标点的价小于6、等于6和大于6的坐标向量长度变化特征(不抽取3D网格边界特征)。其中，拉普拉斯坐标由笛卡儿坐标乘以3D网格的Kirchhoff矩阵(Bollobs，1998)得到。

同时，他们还提出了相邻三角面间基于二面角角度偏移和三角面法向量方向偏移夹角的特征。特征降维包含抽取均值、方差、偏度和峰度4个统计特征，以及直方图相邻bin的插值构成另外4个统计特征。最后，所有特征经过对数变换以提取更为有效的特征，这208维特征简称为YANG208。

尽管YANG208计算成本较低、特征数量较多，但其检测准确率比其他隐写分析特征弱，表明部分隐写分析特征不起作用。此外，YANG208特征对不同嵌入率下的载体载密对的检测准确率波动明显，表明其检测隐写算法不够鲁棒。

4.1.2 Yang40特征

Li和Bors(2016a)有效约简了YANG208，摒弃了若干判决能力较弱的检测子，保留了以下6个特征：笛卡儿坐标系和拉普拉斯坐标系下坐标分量的绝对值。此外，笛卡儿坐标系和拉氏坐标系下各个顶点坐标与网格中心的欧氏距离，以及二面角夹角偏移量为作者设计的另两个隐写分析特征。

从以上10个特征向量中，分别计算统计特征(均值、方差、偏度和峰度)，最终得到40维隐写分析特征。与YANG208相比，YANG40特征在特征维数下降的情况下仍能保持较好的隐写分析性能。

4.1.3 LFS52特征

Li和Bors(2016a)提出了基于局部特征集合(local feature set, LFS)的有效特征，共含有52维，简称为LFS52。第1个特征为顶点法向量的偏移量。由于网格表面局部形状曲率能表达网格表面光滑度，因此提出了基于曲率的隐写分析特征。由于最小主曲率和最大主曲率能够反映局部曲面顶点的弯曲程度，因此第2个特征为高斯曲率(Rugis和Klette，2006)偏移量特征，其中高斯曲率为最小和最大主曲率的乘积。曲率比是最小主曲率与最大主曲率之比，并将曲率比偏移量作为第3个特征。

与基于坐标和三角面法线的隐写特征相比，基于顶点法向量和曲率的特征有更强的检测能力。

4.1.4 LFS64特征

Kim等人(2017)在LFS52特征的基础上，提出了坐标顶点法向量方向偏移特征、高斯曲率值变化特征以及最小主曲率和最大主曲率的曲率比值变化特征，包含64维特征，简称为LFS64。

该方法性能明显优于LFS52特征，是由于增加了边法向量、中值曲率和总曲率特征。

4.1.5 LFS76特征

Li和Bors(2017)在LFS52基础上进一步提出了球坐标系下坐标分量值变化特征，简称为LFS76。其中，球坐标系下坐标点与原点的欧氏距离、方位角和仰角的偏移量为新的3维特征。球坐标系下三角面的边长分量的偏移量为另外3维特征。

通过实验发现，就针对检测隐写算法的隐写分析性能而言，LFS76特征性能并不优于LFS64特征，说明这6维新的特征并不能有效检测隐写扰动。

4.1.6 ELFS124特征

Li和Bors(2020a)在LFS76特征的基础上，提出了基于边长变化和边长分量变化特征，简称为ELFS124。笛卡儿坐标系和拉氏坐标系下分别计算3种特征：三角面边向量偏移量(模长的差、差的模长和向量差的向量夹角)，最后形成了新的12维特征。

LFS124的计算复杂度非常低，而且隐写分析性能有了明显的提升，这说明三角面边向量容易受到隐写扰动的影响。

4.1.7 法向量投票张量(normal voting tensor, NVT)+特征

Zhou等人(2021a)提出代表邻域的元素，能够更敏感地察觉 3D 坐标点隐写扰动造成的影响。由于坐标点或三角面代表的元素涵盖区域面积不够大，他们采用三角面一环邻域区域作为单位元素设计隐写分析特征。通过分析三角面邻域相关性，提出了基于三角面邻域法向量张量投票模型的特征以提升3D网格隐写分析性能。

Zhou等人(2021a)设计了三角面法向量的张量投票模型，并通过对张量矩阵特征值分解得到3个特征根。特征根的偏移量即为最后的隐写分析特征。将该特征与LFS76特征级联得到100维的NVT+隐写分析特征。由于特征值能够反映局部3D表面形状的凸起程度，例如尖角、尖锐的边缘或平面，因此NVT+能够更为有效地检测隐写算法。

NVT+明显地提升了隐写算法的检测性能，同时表明三角面法向量是一个相当有效的隐写分析检测指标。其唯一的缺点是，由于搜索相邻三角面非常耗时，因此该算法的复杂度非常高。

4.1.8 WFS228特征

Li和Bors(2020b)提出在3D网格原始模型与其分别上采样得到的高分辨率网格和下采样得到的低分辨率网格经小波分解后的系数变化和边长变化的特征，简称为WFS(3D wavelet feature set)228。

通过采用3D懒小波分解(Lounsbery等，1997)和蝴蝶方案(Dyn等，1990)得到的小波系数向量，可用于表示不同分辨率下的3D网格特征。由于与小波变换相关的水印嵌入方法基本上是通过修改小波系数和3D网格的边来实现秘密消息的嵌入，因此这种方式得到的特征能有效地检测3D网格隐写算法。此外，可通过分析原模型更大的顶点邻域，得到高分辨率的3D网格模型，这种高分辨率模型相比于原网格模型对隐写扰动更敏感。

该算法提出了基于边向量和小波系数向量的3种不同分辨率下的隐写分析特征。WF228特征隐写分析性能优于LFS76特征，但劣于NVT+特征。该算法复杂度也较高，是因为需要搜寻近邻的坐标点。

4.1.9 特征筛选

Li和Bors(2016b)、Li等人(2018)通过特征选择来解决载体来源失配问题(cover source mismatch, CSM)。

Li和Bors(2016b)首先对原始3D网格进行了简化和加噪处理，并对预处理后的3D网格隐写。然后，采用皮尔逊相关系数等技术分析载体和载密网格的差异程度，最后选择有效的隐写分析特征。

4.2 专用型隐写分析

专用型隐写分析主要检测特定隐写算法，包括针对基于PCA旋转变换的隐写和置换隐写的检测。

4.2.1 针对基于PCA旋转变换隐写的隐写分析

Zhou等人(2019)指出一系列基于PCA变换预处理隐写算法的安全漏洞：预处理后的载密模型和未经过预处理的载体模型是容易受到针对性隐写分析方法检测的。对于任意一测试模型，通过分析其旋转至PCA主轴和次轴构建的空间的旋转矩阵，能高效地检测其为载体或载密。

4.2.2 针对置换隐写的隐写分析

Wang等人(2019)发现置换隐写容易导致3D模型存储结构上相邻坐标点失去近邻特性，因此，他们提出基于存储结构上相邻坐标点在空域中的距离度量值作为特征，以实现隐写检测。

此方法在检测不同置换隐写算法时是通用的，并不需要任何先验知识，比如具体的隐写方法或者固定的嵌入率。

4.3 算法比较

如图3所示，本节分析了不同隐写分析方法的实验结果。实验中采用了两种数据集：普林斯顿分割集和普林斯顿网格。训练过程中，分别对训练集的载体和载密网格提取隐写分析特征，并用集成分类器训练特征。测试过程中，预测测试集的载体和载密网格的分类结果。

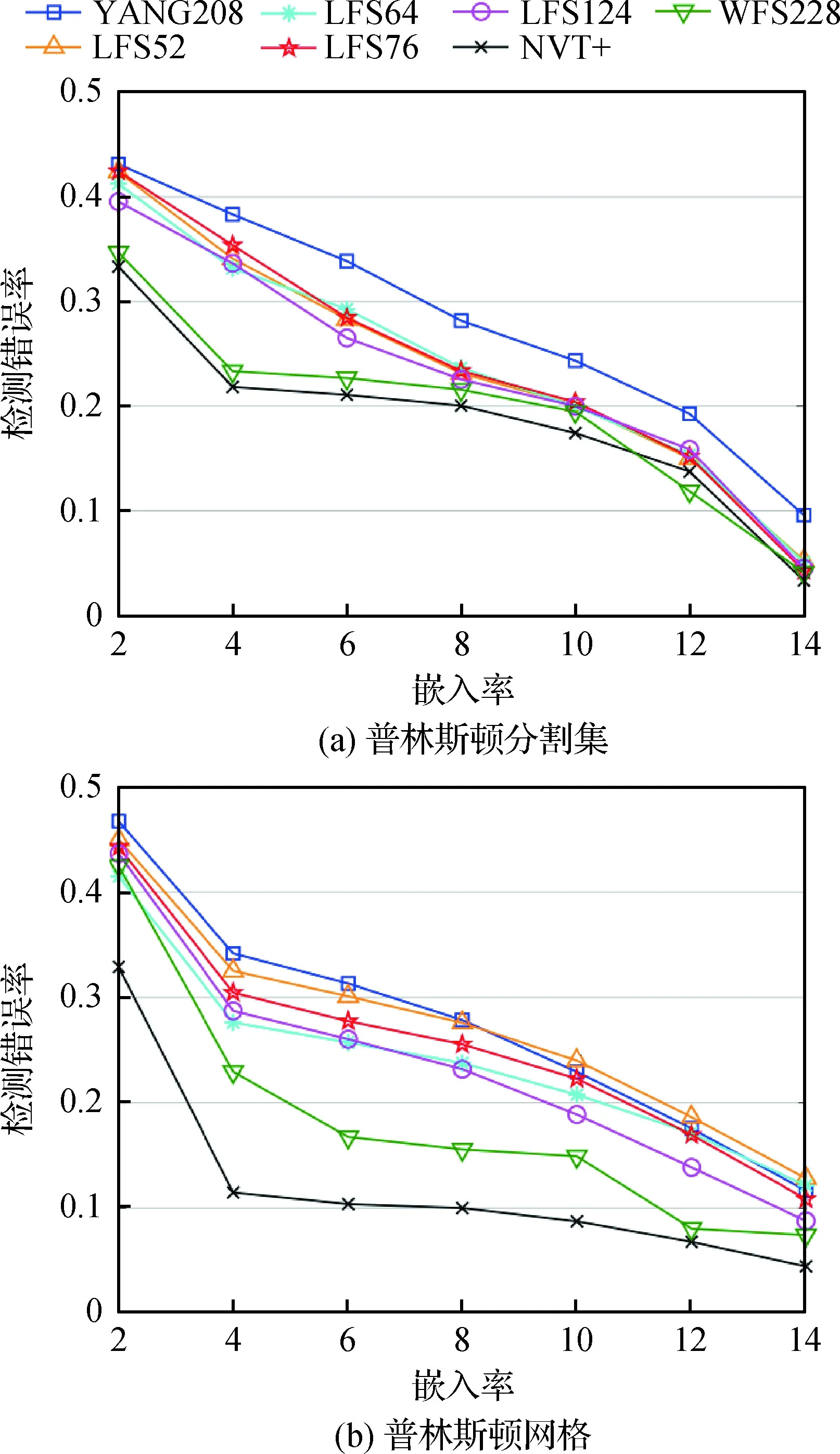
图3 3D网格隐写分析性能比较Fig.3 3D mesh steganalysis performance comparison((a)Princeton segmentation benchmark;(b)Princeton ModelNet)

此外，普林斯顿网格数据集上的平均检测错误率低于普林斯顿分割集上的结果。出现差异的原因在于数据集类型不同：前者是计算机辅助设计(computer-aided design, CAD)技术人工制作而成；而后者是对自然物体扫描重建而得的模型。结果表明，3D模型表面越平整，越不适合秘密消息的嵌入。

5 结 语

面对快速发展的隐写分析和深度学习技术，3D模型隐写的相关研究仍有值得开拓的空间。

5.1 3D模型隐写

实现更高的隐写安全性是3D网格隐写的目标，本文提出以下改进的方向：

1)融合扰动隐写和置换隐写算法。联合置换隐写和最低有效位隐写是提升隐写安全性的方法。实验表明，当网格的顶点数达到5 000时，置换隐写最大嵌入率达到11 bpv，为大容量隐写。随着嵌入率的增加，抗通用隐写分析和置换隐写分析的安全性也随之下降。因此，如何在两个域中分配消息长度，是设计更优3D网格隐写算法的关键。

2)设计非加性失真函数模型。图像自适应隐写算法的最新研究表明，利用相邻元素之间的相关性提升隐写算法的安全性，称为非加性失真模型(Li等，2015；Denemark和Fridrich，2015)。如何对坐标点设计联合失真，并利用 DeJoin(Zhang等，2017)算法在x,y,z分量上分配消息长度，最后利用校验栅格编码(Filler和Fridrich，2011)嵌入消息，是实现高安全隐写算法的方式。

3)设计3D网格批隐写算法。批隐写和池化隐写分析问题是隐写领域中的公开问题(Ker，2006)，是一类批数据的隐写和隐写分析问题。对于图像隐写而言，安全隐写容量与载体长度的平方根成正比(Ker，2007)。探究3D网格的安全容量与顶点数量之间是否存在上述关系则是一个具有挑战性的问题。

5.2 3D模型隐写分析

1)设计3D通用隐写分析富模型。由于低嵌入率下的两态调制隐写和最低位隐写算法得到的载密网格模型不容易被目前最优的隐写分析算法检测到，因此，隐写分析算法存在较大的改进空间。Fridrich和Kodovsk(2012)提出的富模型特征是基于多个线性和非线性高通滤波器和高维量化噪声残差特征设计的，能有效检测载密图像。受其启发，可以利用更多的3D网格平滑技术提取更为丰富的残差特征。这些技术包括早期经典的平滑方法，例如去噪和抹平(Botsch等，2010)，以及最新的曲面平滑技术，例如各向异性扩散流(Bajaj和Xu，2003)、双边滤波(Fleishman等，2003)、非线性平滑(Eigensatz等，2008)和基于神经网络的滤波方法。

2)设计基于深度学习的隐写分析方法。迄今为止，3D网格隐写分析都是基于人工设计的特征实现的检测，而人工特征设计较为复杂，不易于短时间内设计得到。近年来，深度学习在多种机器学习分类问题上展现了卓越的性能。深度神经网络从大量的训练数据中学习模型和分类测试数据，例如卷积神经网络(convolutional neural network, CNN)(Krizhevsky等，2012)和图卷积网络(graph convolutional network, GCN)(Hamilton等，2017)等。因此，设计针对3D隐写分析的端到端学习的神经网络， 是实现更有效的隐写分析性能的解决方案。