基于某车型车顶瘪塘问题的分析与解决
杨杰 代朝刚 李佳旭








摘 要:本文基于某车型行李架安装导致的车顶瘪塘问题,通过对车顶行李架系统的结构分析建立了车顶變形量公式,提出了减小泡棉有效接触面积和减小泡棉弹性模量两种解决方案,并通过实车试验和有限元仿真验证了方案的有效性,最终解决了该车顶瘪塘问题。
关键词:行李架 车顶瘪塘 泡棉 有限元仿真
Abstract:Based on the roof deformation problem after roof rack’s assembling, this paper analyzed the construction of roof rack system and built a formula of roof deformation. Two solutions were raised and verified through real car test and finite element model simulation. One solution is to reduce the contact area of roof rack foam. The other solution is to reduce the elastic modulus of foam. The proposed schemes have successfully solved the roof deformation problem.
Key words:roof rack, roof deformation, foam, finite element model simulation
1 引言
随着SUV市场的逐渐扩大,自驾游和家用储物需求也与日俱增,车顶行李架的运用不仅弥补了车后行李舱空间的不足,也给SUV车型增加了运动感和时尚感[1],行李架变成了各大主机厂SUV车型的标准配置。在主机厂车间行李架安装过程中,车顶瘪塘已经成为各大主机厂的普遍问题,瘪塘现象为客户可感知外观缺陷,在车型预批量阶段亟待解决。某主机厂某车型在预批量生产阶段在未安装行李架前车顶无瘪塘现象,当使用拧紧枪安装完行李架后,在固定点之间的区域发现明显的车顶瘪塘,且发生瘪塘的概率为80%,针对这一常见问题,本文将系统分析车顶瘪塘产生的原因并提出相应的解决方案。
2 车顶瘪塘成因分析
2.1 结构分析
如图1所示为某车型车顶贴附式行李架,贴附式行李架即行李架底面与车顶完全贴合,图2为该行李架的车身固定方案,行李架通过拉铆螺母、车顶钣金、车顶钣金加强板、螺母固定到车身钣金。在行李架底部设计了EPDM泡棉(见图3),其作用为密封、防尘和外观缝隙遮蔽等,其与车顶为过盈设计,有一定的预压缩率,预压缩率一般为30%-50%。
针对该车型行李架造型进行分析,导致车顶瘪塘变形主要有两个因素:一为螺母拧紧过程中对固定点区域的压力;二为行李架安装过程中和安装后固定点之间泡棉与车顶钣金过盈配合,泡棉对车顶产生的压力,因此车顶瘪塘发生区域有两种,如图4中的区域A和区域B。在固定点附近的区域A由于有车顶钣金加强板(如图2所示),车身强度较高,不易瘪塘,但在非固定点区域B,车顶钣金强度相对较弱,车顶容易产生变形,本文某车型瘪塘即发生在区域B。
2.2 车顶瘪塘公式
由行李架结构分析可知,导致车顶瘪塘抱怨的车顶变形量Δ与各因素之间的关系可以描述如下:
其中:
Δ:由行李架安装导致的车顶变形量;
:密封泡棉的弹性模量,对于EPDM发泡材料来说,其弹性模量与压缩时间及压缩率相关,非恒定值;
:实际压缩状态泡棉与车顶的有效接触面积;
:泡棉实际压缩率;
:车顶刚度;
:车顶变形系数,对某一特定车型而言该系数为恒定值;
:初始泡棉厚度;
:行李架安装后泡棉厚度;
对于车顶刚度而言,预批量阶段的车顶钣金材料、厚度、油漆工艺方案和车身强度已确定,且与整车碰撞性能相关,一般在车辆预批量阶段不宜做设计更改,本文则主要从车身钣金以外的因素进行分析优化来解决车顶瘪塘问题。
泡棉压缩率与泡棉的密封性能息息相关,大部分半闭孔和闭孔泡棉实现密封功能的压缩率范围为30%-50%。通过减少泡棉压缩率为40%、30%、20%,实车安装测量车顶变形量,发现该范围的变化对车顶变形量的变化影响较小,压缩率的更改无法解决本文某车型的瘪塘问题,因此试验数据不做赘述。
对于泡棉弹性模量而言,不同种类的泡棉弹性模量的性能差异较大,闭孔/半闭孔之间的差异也极大,为车顶变形量的关键因素,车型瘪塘的解决方案则可从此因素着手,此项为一般考虑项。
泡棉与车顶的有效接触面积为另外一个影响车顶瘪塘变形的重要因素,在解决瘪塘问题时以泡棉的密封性要求及外观要求为前提,保证必要的有效接触面积,然后在此基础上根据泡棉的弹性模量/压缩率设法较小泡棉的面积。
综上所述,针对由行李架引起的车顶瘪塘问题,主要的解决途径有两个:一是减小泡棉的弹性模量;二是减小泡棉的有效接触面积。本文将以某车型为例,从实验和仿真两方面进行两种途径的详细分析和验证。
3 解决方案
上一章节我们分析了车顶瘪塘的具体原因,并找到了主要解决途径,具体解决方案主要有如下两种。
3.1 减小泡棉的有效接触面积
如图3所示,为本文某车型行李架的泡棉,与车顶的有效接触面积为459cm2,根据公式(1),我们可以通过减小泡棉与车顶的有效接触面积来减小车顶的变形量,解决方案为将泡棉切割,切割后的有效接触面积为240 cm2,如图5所示,在压缩量不变的情况下压缩应力可降低47.8%。由此推测,车顶变形量也可相应降低47.8%。
接下来将通过实车验证该方案对车顶瘪塘的有效解决。
3.2 减小泡棉的弹性
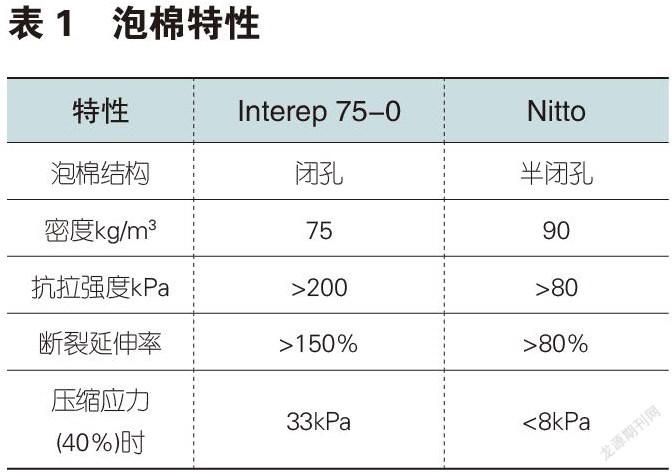
本文瘪塘问题车型采用的泡棉为Interep 75-0闭孔泡棉,在40%压缩率下压缩应力为33kPa,根据公式(1),我们在不改变该车型压缩时间与压缩率的前提下,减小泡棉自身的弹性模量,即减小泡棉的硬度,采用硬度相对较小的Nitto EE-1010泡棉,在40%压缩率下压缩应力为8kPa,其参数对比见表1,在压缩量不变的情况下理论压缩应力可降低75.6%,由此推测,车顶变形量也可相应降低75.6%。
后文将进行实车装车试验来验证该解决方案的有效性。
4 试验验证
本章将依据上述理论分析方案进行试验验证。因为行李架铝杆本身的刚度远大于车顶,其在安装过程中因泡棉挤压而产生的变形与车顶变形量相比可忽略不计,所以这里直接通过测量行李架与车顶之间的缝间隙来评估车顶变形量。为排除初始车顶偏差及零件尺寸偏差,以一组无泡棉行李架安装后的间隙值作为基准点,通过式(2)间隙变化值来量化评价不同措施方案对减小车顶瘪塘的效果。
其中
:不同方案行李架与车顶之间的间隙值;
:无泡棉行李架与车顶之间的间隙值;
:间隙变化值;
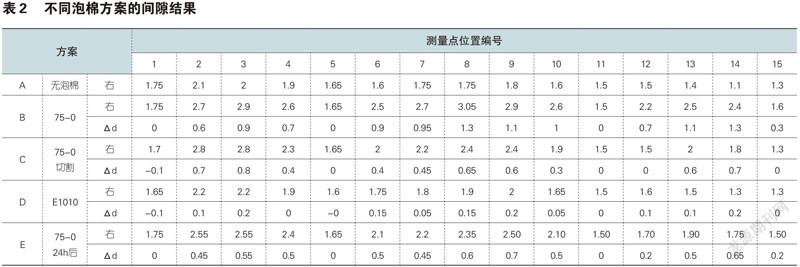
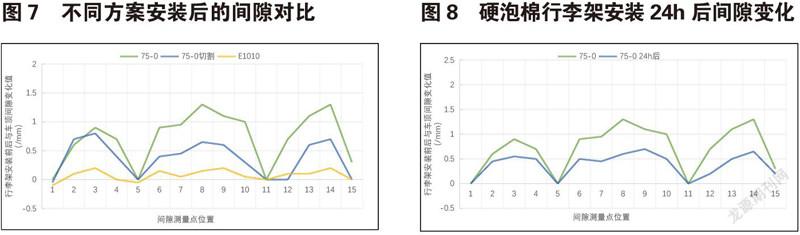
具体实施如上图6,在行李架固定点1-2,2-3,3-4之间均匀选取测量点15个,分别测试四种方案行李架安装后的间隙值,评价不同方案对车顶瘪塘的优化效果。五组测量结果为:A)无泡棉间隙,即基准间隙值;B)75-0,即硬泡棉间隙值;C)75-0切割后间隙值;D)E1010,即软泡棉的间隙值;E)75-0 24h后,即硬泡棉安装24小时后间隙值。试验结果见表2和图7。
4.1 减小泡棉有效接触面积的实车验证结果
从图7中可以看出,原始状态泡棉安装后,泡棉挤压导致车顶的最大变形量1.3mm在8号点,如使用切割泡棉,测量点8变形量减少到0.65mm,变形量减小约50%,与2.1节的推测结论一致,车顶瘪塘明显改善,但0.65mm的变形量导致的车顶瘪塘依然被明显感知。
4.2 减小泡棉弹性的实车验证结果
若采用半闭孔软泡棉,从图7中可以看出,测量点8变形量降至0.2mm,变形量减小约85%,与2.2节的推测结论一致,且0.2mm的变形量较小,视觉无法感知,车顶瘪塘问题有效解决。
综上,最终采取方案二,有效解决了车顶瘪塘问题。
4.3 压缩应力下泡棉弹性变化对瘪塘问题的影响
需要指出的是,在解决实际工程问题过程中,还需要考虑泡棉固有特性,即其在承受持续的压应力作用下,模量会随时间逐渐变小。
此特性表现为行李架安装一段时间后所受到的泡棉挤压力将逐渐减少,车顶瘪塘现象将得到改善。从实车验证结果图8可知,闭孔泡棉75-0在安装24小时后测量点8变形量从1.3mm減至0.6mm,减小约53.8%。实际工程应用中,当出现轻微的瘪塘现象时,可以放置24小时之后再进行评价,其瘪塘现象通常会消失。
5 有限元仿真验证
使用有限元计算的方法对实际问题进行仿真,并将潜在措施在虚拟环境下进行验证,通常可以有效节约试验资源,大幅提高问题解决效率[2]。在解决车顶瘪塘问题过程中,也引入了有限元仿真方法,如图9为车顶行李架系统瘪塘有限元仿真模型。
对车顶钣金、行李架主杆、行李架泡棉划分网格[3]。在车顶钣金周边焊接处及行李架加强板处设置约束,在行李架主杆与泡棉、泡棉与车顶之间设置接触。在建模前处理过程中将行李架沿Z向移动+3mm,并在计算过程中将Z向-3mm位移载荷加载至行李架,以此准确模拟行李架安装过程中泡棉对车顶的挤压作用。
使用该模型计算车顶钣金受泡棉挤压的变形量,复现初始75-0泡棉车顶瘪塘的问题,并验证E1010和切割的75-0泡棉两个方案的改善效果。为便于比较,选取行李架边缘处的车顶变形量并作曲线评估。
此外需要指出,有限元模型基于零公差的理想状态建立,无法模拟实际生产过程中的诸多因素。鉴于车顶变形量仅约1mm,相对车顶整体尺寸(约2000mm)非常小,且车身制造存在公差,试验测量也存在误差,因此仿真得出的车顶变形量与试验测得的车顶变形量在数值上直接对比的意义不大,相比之下同为仿真环境下的多工况对比则更有参考意义。
除用于解决实车车顶瘪塘问题外,在前期开发过程中,应用该模型将新项目与过往项目进行对比,可以对新项目方案在预批量阶段发生车顶瘪塘问题的风险进行评估,从而为行李架系统开发提供有益指导。
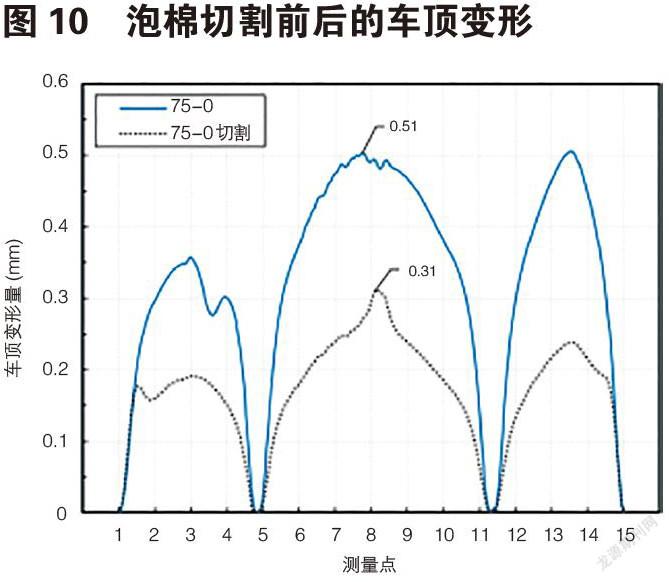
5.1 减小泡棉接触面积
图10对比了75-0泡棉切割前后的车顶变形情况。对行李架中心位置观察,对应试验测量点8。未切割泡棉的行李架在测量点8引起的车顶变形为0.51mm,切割泡棉的行李架引起的车顶变形为0.31mm,变形量减小39.2%,与2.1节分析得出的结论47.8%和3.1节实车试验的结果50%较为一致,车顶瘪塘得到有效改善。
相比试验中15个离散的测量点,有限元模型可以得到连续的车顶变形情况。在图10切割后的75-0泡棉工况中,测量点8处的车顶变形量相较前后的测量点有明显增加(约0.05mm),这是由于此处位于第二、三段泡棉的连接处(图11),无法被切割,而测量点8位于行李架中心位置,为车顶瘪塘问题最为严重的区域。即切割泡棉的方案本身具有一定局限性,限制了它的实际改善效果。
通过以上分析可以得出,通过切割泡棉来减小车顶变形时,除了切割面积的大小外,还需要考虑切割区域的分布情况,未被切割的区域依旧会引起较大的车顶变形。
5.2 减小泡棉弹性
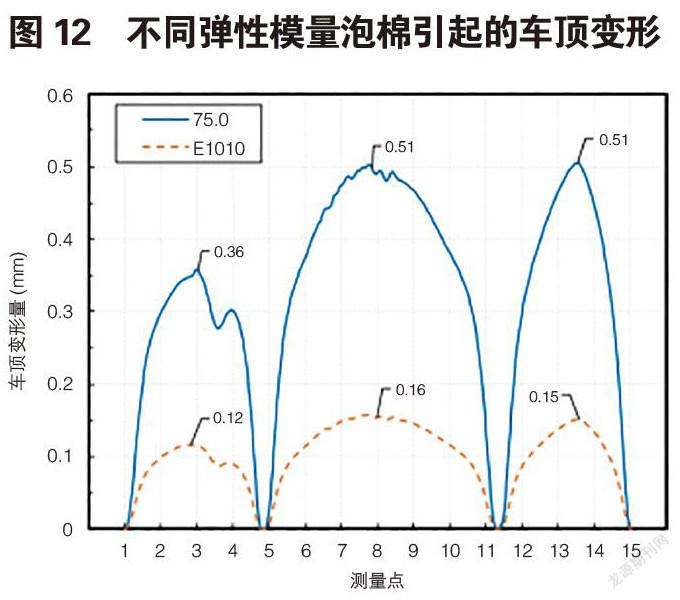
图12对比了两种不同弹性模量泡棉引起的车顶变形情况。原始75-0泡棉行李架在测量点8引起的车顶变形为0.51mm,弹性较小的E1010泡棉行李架在测量点8引起的车顶变形为0.16mm,变形量减小68.6%,与2.2节分析得出的结论75.6%和3.2节实车试验的结果80%较为一致,车顶瘪塘明显改善,问题得到解决。
根据仿真结果进一步分析泡棉弹性对车顶变形的影响规律。除了测量点8为瘪塘最严重的区域外,选择行李架第一、二固定点和第三、四固定点之间的车顶变形量进行比较,分别对应试验测量点3和13。测量点3处75-0和E1010引起的车顶变形量分别为0.36mm和0.12mm;测量点13处75-0和E1010引起的车顶变形量分别为0.51mm和0.15mm。即测量点3、8、13处的车顶变形量通过降低泡棉弹性分别减小了66.7%、68.6%、70.6%,十分接近。结合图12中75-0与E1010两条曲线趋势基本一致,不难看出E1010近似为75-0等比例降低。
通过以上分析可以得出,泡棉弹性模量与车顶变形量存在近似线性关系,降低泡棉弹性模量对解决车顶瘪塘问题具有显著效果。
6 结论
依据本文提出的车顶瘪塘公式及试验验证得知,解决行李架导致的车顶瘪塘问题,可以考虑减小泡棉的有效接触面积或采用低弹性模量的泡棉,后者效果更佳。另外,本文建立了一种行李架车顶瘪塘有限元仿真模型,相较试验可以获得更细致的结果,在解决实车问题时可以评估措施的有效性,也可以在项目前期开发过程中预判发生车顶瘪塘风险。
参考文献:
[1]葛广凯. 汽车行李架结构解析[J]. 汽车实用技术.2017(08):12-14.
[2]姜伟民,袁一平. 基于有限元CAE分析法对B灯支架强度受密封垫挤压变形的研究[J].时代汽车. 2019(10):116-118
[3]唐振华. 车载行李架结构的有限元分析法[J]. 技术专栏. 2017(12):45-51.

