基于改进粒子群算法的农业机械产品装配分组优化配置
,
(晋中信息学院,山西 晋中 030800)
0 引言
农业机械产品装配分组配置的精度要求较高,精度过低不仅会导致产品出现质量问题,也会威胁到相关员工的人身安全[1]。尤其是在生产机械产品过程中,在确保产品质量的同时尽可能将成本降到最低,因此在引入设备过程中需要对设备进行约束,利用装配技术加强配置精度[2]。装配就是将零件进一步加工,通过零件配置生产出精度更高的产品,减少零件库存量,降低损失的同时优化新设备的成本[3]。因此,对农业机械产品装配分组优化配置进行研究有重要意义。
鲍学英等[4]参考施工机具台班费用定额数据以及PAS2050规范,基于CLCD数据库信息,利用熵权法基于指标数据计算出目标偏好权重;使用经过均匀设计以及自组织映射改进过的遗传算法对新型机械配置优化模型进行求解计算,实现机械优化配置。于绍政等[5]首先分析并计算出可能影响机械配置关键参数以及干扰因素,在加强机械性能的基础上构建机械优化配置仿真模型;其次提出机械调度算法进而确保模型的真实性以及有效性;最后将成本最小化视为最终目的进行模型求解,实现机械产品装配分组优化配置。
以上2种方法在构建机械配置模型过程中未对配置过程进行约束,更没有建立专属的配置约束函数,因此,配置过程中难免因为相关条件的约束出现配置偏差过高和效率过低等情况,导致农业机械产品产出率低和配置性能低等问题出现。
为了解决上述方法中存在的问题,提出基于改进粒子群算法的农业机械产品装配分组优化配置方法。
1 农业机械产品装配分组优化配置模型
1.1 机械产品零部件质量公差分组
将农业机械产品零件作为研究基础,以机械产品为依据计算出零件之间的公差,基于公差划分出零件的等级[6-7],分别为一级、二级和三级,其主要区别就是与新品公差之间的大小,一级公差差值为0,二级公差差值为φ,三级公差差值为γ,且γ>φ>0。
1.2 尺寸链约束
为提升农业机械产品的质量,需要保证配件的精度,因此本文根据装配尺寸链分析零件以及装配的精度[8]。假设农业机械产品装配所需零件共计n个,其中形成的闭环尺寸链共计m个,通过极值法分析尺寸链可知,要求闭环的尺寸标准大于等于增环和以及减环和之间的差值,将此标准标记为Ai,其表达式为
(1)

封闭环尺寸的精度标准最大值和最小值分别大于等于增环最大与减环最小尺寸和之间的差值,以及小于等于增环最小与减环最大尺寸和之间的差值,其表达式为
(2)
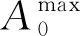
1.3 质量损失-公差函数
不同精度等级的装配零件因公差的不同会导致目标值出现误差[9],而由于不同误差生产出的农业机械产品的质量也不尽相同,根据产品质量特点构建出针对此产品的零件损失-公差函数,利用定量分析方法得出每种精度等级下零件的质量损失程度。
将产品所需的n个零件进行分级,假设零件为xi(i∈[1,2,…,n]),零件的等级分别为xi1、xi2和xi3,则公差函数的表达式为
(3)
f(xi)为零件xi所要达到的使用目标值;f(xij)为xi每种精度等级下出现的误差;ki为质量损失函数中的常数项。
其中,质量损失函数[10]中常数项ki的表达式为
(4)
Bi为零件xi无法使用后的损失;Δi为零件xi中公差的最大值。
1.4 装配成本函数
不同等级下的零件价格以及装配价格均有差别,因此,不同精度要求的零件配置其成本也不一样,则每种配置的总成本目标函数为
(5)
G(xij)为零件xi的精度等级为j时的装配价格;C(xij)为零件xi的精度等级为j时的购买价格。
1.5 农业机械产品装配分组优化配置约束函数
根据零件之间公差,分出精度等级,在配置过程中添加其尺寸链、成本以及损失函数等条件,并要求最终配置成本为最小,进而构建出机械产品配置约束函数,其表达式为
(6)
其中的条件为
(7)
式(6)和式(7)为约束函数,也可以将其作为农业机械产品装配分组配置模型,即可完成装配分组优化配置模型的构建。
2 基于改进粒子群算法求解模型
改进粒子群算法是根据鸟群捕食的跟随情况进行求解,粒子根据飞行情况寻找出问题的最优解,此算法更新出新群体的表达式为
(8)
Pg为求算过程中整体的最大值;vn为d维度时粒子i的当前速度;Pi为求算过程中独立个体的最大值;vo为d维度时粒子i的上一次速度;r1和r2均为0到1之间的任意数;S1、S2为初始与当前的学习因子;w为惯性权重;Xd为目前粒子的位置。为了进一步优化算法性能,需要对粒子群算法进行改进,具体的改进过程如下。
2.1 动态归档极值更新外部集
动态归档技术的本质就是将目前最优的粒子添加到当前计算中,保证最优个体的持续性以及群体的优良性,进而避免群体的退化问题。

(9)
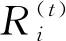
利用式(8)不断更新群体,并根据所有粒子和群体位置得出各个粒子的序号,进而加强种群的优良性,使得粒子不断优化,最终获取无限接近Pareto前沿的解集[11]。
2.2 极值更新
粒子群算法具有收敛性高、鲁棒性好以及容易计算的优点,但其缺点是易陷入局部收敛,因此在计算过程中需要添加小生境共享机制。其实质就是利用2个个体间相似性的共享适应度函数计算出群体内个体的适用度,保证在后续的进化中,粒子群算法可依照目前的适应度进行计算,进而确保种群进化后的多样性。
(10)
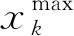
假设共享函数方差为σs,在欧氏距离dij以及σs的基础上搭建的共享函数,该函数的表达式为
(11)
α为共享函数的系数;T为共享函数中自变量的数量;q为共享函数最优结果的数量。
为扩大共享机制的应用范围,需提前运算出属于各个粒子个体的适应度。
将所有共享函数进行相加,即可求解出各个粒子的小生境数,其表达式为
(12)
i为粒子的序号;hi为粒子的小生境数。
在初始适应度以及hi的基础上求解出共享适应度,其表达式为
(13)

通过共享机制的粒子群算法,可保存所有粒子的适应度值,再通过轮盘赌即可提取出全局最优解,即最优的Pareto前沿。
2.3 模型求解的过程
a.将个体极值、粒子群、参数初始化和速度进行初始化处理,并生成任意的原始群体位置。
b.在目标函数的基础上分别运算出每个粒子的适应度。
c.对Pareto解集进行排除,搜索出原始群体内的非支配解集,并将其保存。
d.通过适应度共享机制运算出粒子群的小生境数以及共享适应度。
e.不断运算生成全新的粒子个体极值,假设粒子目前更新位置的平均适应度值强于前一个,则提取全新的个体极值,否则不改变粒子个体极值。
f.在适应度极值以及轮盘赌方法的基础上得出粒子群最优位置。
g.利用式(8),不断更新出新的群体。
h.辨别目前群体是否能够终止计算,若不满足终止要求则进一步迭代,直到符合条件,输出结果并停止迭代。
i.混合所有群体和保存的粒子,在动态归档方案中提取出最终的进化种群,并利用其替代上一次迭代得出的种群,一直迭代到满足终止要求为止,生成Pareto的最优解集,进而完成粒子群算法,求解出配置模型的最优解,实现农业机械产品装配分组优化配置。
3 实验与结果
为了验证基于改进粒子群算法的农业机械产品装配分组优化配置方法的整体有效性,分别采用本文方法、文献[4]方法和文献[5]方法进行收敛性、农业机械产品产出率和配置性能的测试。
3.1 收敛性
收敛性反映的是能否快速准确地得出输出结果,在同一环境下利用3种方法进行相同农业机械产品装配分组的配置,比较其收敛性,收敛性越高说明其配置越优。一般情况下,适应度值越低,个体越优秀,而利用最优个体保留策略可以获取最优的解,提升算法的收敛性。具体的比较结果如图1所示。

图1 3种方法的收敛性
其中,适应度指的是经过优化配置后产品中可产生的最大误差,最优适应度值为0.1 mm。根据图1可知,与文献[4]和文献[5]的方法相比,在20次迭代时,本文方法的适应度达到了最低值,所以此时获取的结果为最优适应度值计算结果,说明本文方法不仅收敛性好,其精度也较高,是农业机械产品装配分组优化配置的最佳方法。这是因为本文方法在进行产品配置前构建了关于农业机械产品装配分组模型,并利用改进粒子群算法对该模型进行优化求解,保证产品等级以及效率,进而提高配置能力,加强收敛性。
3.2 农业机械产品产出率
农业机械产品装配分组配置的方法就是将目前库存中可利用的零件进一步加工后安装到新品内,最大程度地降低成本损失的同时提高产品产量。为判断优化配置方法的优劣,可比较3种方法利用目前库存量所生成的产品产出率,产品产出率越高也就表明方法越有效,3种方法的产出率结果如图2所示。
分析图2可知,本文方法的产出率在每组实验中都是最高的,说明该方法的零件利用率最高,可将因零件废弃等问题导致的成本损失降低到最小,文献[4]方法的产品产出率要比本文方法低很多,但文献[4]方法产品产出率波动较小,说明其稳定性较好,反观文献[5]方法的产品产出率,不仅波动幅度过大,且产出率过低,十分不利于产品的配置,不仅最终的损失过大,其质量也不能得到保障,因此证明本文方法的能力是最强的。

图2 3种方法的农业机械产品产出率
3.3 配置性能
在相同环境下通过3种方法对10组样本进行配置,对每组样本进行200次优化计算,得出3种方法在每次实验中所用的总耗时,耗时越小,说明方法的效率越高,比较结果如表1所示。

表1 3种方法配置的总耗时
根据表1可知,本文方法在每次实验中的总耗时均是3种方法中用时最少的,其余2种方法每组实验的总耗时均超过本文方法,验证了本文方法的配置效率是最佳的。
产品的质量是产品的前提要求,但产品的稳定性是企业可持续发展的硬性标准,标准差正是验证算法稳定性的主要方法,标准差的结果越小说明每次配置的结果精度差别越小,其稳定性也就越高,配置性能越优,否则相反,具体的比较结果如图3所示。

图3 3种方法精度的标准差
根据图3可知,本文方法的标准差最小,表示该方法配置结果之间的精度非常相近,其稳定性较优,其他2种方法较本文方法均不稳定,从而验证本文方法的具有较好的配置性能。
4 结束语
各个行业中的机械产品均是由各种零件组装产生的,但由于设备的不断更新,会剩余很多老旧设备的零件,且为了提升新产品装配效率,降低成本,减少损失,因此提出基于改进粒子群算法的农业机械产品装配分组优化配置方法。该方法构建出机械产品配置模型,利用改进粒子群算法求解该模型,实现农业机械产品装配分组优化配置。实验结果证明,该方法可以解决收敛性低、农业机械产品产出率低和配置性能低的问题,为大幅度降低成本,提高利润奠定坚实的基础。

