基于时频分析的移频轨道交通信号检测方法
(中铁第一勘察设计院集团有限公司通信信号设计院,陕西 西安 710043)
0 引言
现如今,随着社会生活水平的快速提升,人们出行形式多样[1]。当城市中轨道处于饱和状态时,轨道电路在列车信息传递和指挥中发挥重要作用。移频轨道信号的检测可以及时避免故障的发生,保证列车正常运行。因此,如何有效地对移频轨道交通信号进行检测,成为该行业亟待解决的问题之一[2]。
文献[3]提出基于视觉的轨道交通信号灯识别算法,该方法由于未能利用时频分析法获取交通信号的时频特征,导致信号的检测精度低;文献[4]提出基于无监督学习的NLOS信号检测方法,该方法在进行聚类划分时存在一定问题,导致检测误差高;文献[5]提出指数型随机共振微弱振动信号检测方法,该方法在进行逃逸率分析时存在一定误差,所以检测时的噪声频率不稳定。
为解决上述信号检测时存在的问题,提出基于时频分析的移频轨道交通信号检测方法。
1 时频分析的信号特征提取
基于时频分析方法对移频轨道的交通信号特征进行提取[6]。时频分析中通过短时傅里叶变换确定信号的整体时频信息,并对多分辨的信号进行变换。
1.1 短时傅里叶变换
首先,设定移频轨道交通信号中t时刻的变信号为f(t),信号的短时变换过程为
(1)
F(ω,τ)为变换后的交通信号,表示交通信号在τ时刻时间轴上的局部频谱;g(t)为映射过程中的窗函数;R为变换时信号指数;e为信号数量;(ω,τ)为f(t)映射的时频平面;d为信号的长度;j为整数。在此过程中,随着窗函数的平移,获取交通信号的f(t)整体时频信息。
将hamming窗口的长度设定为L=[16,128],对交通信号的波形进行变换;基于灰度图对交通信号的幅度进行表示[7]。过程中,窗口长度越小,信号的分辨时间越长,而信号的分辨率就越差;窗口若较大,信号的分辨率就会变高,以致无法对信号进行分辨;所以需利用固定分析窗对信号的时频分辨能力进行制约,并对信号中时、频2个窗口进行折中处理。
1.2 多分辨分析
依据正交小波基对信号的L空间进行近似信号的逼近表示。将交通信号中近似信号进行整合,作为信号的平滑样本。近似信号大多是从不同的尺度上获取,所以利用小波包变换原理划分交通信号,使交通信号能够进行完整的多分辨分析。
利用小波包变换方法对交通信号进行分解,提取信号的频率信息。依据小波包变换将交通信号分为64个尺度,6个层次;且各个尺度都具有fw=fs/2/64=31.25 Hz频带。分解后的信号时频分布如图1所示。
依据图1可知,信号在分解时,无法对信号进行正常分解。在进行分辨率分析时,该信号也会遭受来自测不准原理的抑制,导致信号的时、频域信息无法兼顾。

图1 信号时频分布
1.3 多分辨的信号变换
基于上述分析可知,交通信号的信号能量普遍处于信号的低频位置,基于短时傅里叶变换方法,以交通信号中低分辨率为基础,获取信号的时间分辨率[8]。首先基于多分辨分析方法将信号分解为不同尺度的若干信号分量;再将获取的尺度分量进行对应的短时信号变换,将变换结果进行叠加处理,获取信号完整的时频构造;最后基于优势互补原则,对信号频率信息进行整合,获取信号准确时间量。
依据正交分解法分解交通信号,过程为
(2)
f′(t)为正交分解后的交通信号;J为信号中的频带总数量;fj(t)为第j个交通信号的信号分量。
利用尺度分析窗口gj对不同尺度的信号分量进行变换,过程为
(3)
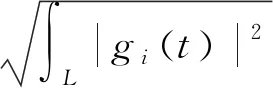
2 移频轨道交通信号检测
基于获取的信号时频特征,利用卷积神经网络对信号进行分类处理,从而完成移频轨道的交通信号检测[9]。
2.1 信号双谱
根据信号特征,获取信号概率密度f(x)特征函数,过程为
(4)
Φ(ω)为信号概率密度的第一特征函数;Ψ(ω)为与其自然对称的第二特征函数;In为二者的对称数量;E为信号的特征;ejωx为交通信号中第j个信号中ω频率上随机变量x的特征。
设定交通信号的k维随机向量为X=[x1,x2,…,xk]T,与信号概率密度函数f(x1,x2,…,xk)相结合,完成信号r阶累积量以及k阶累积的获取,再对信号的随机过程{x(n)}进行设定,x1=x(n),x2=x(n+τ1),…,xk=x(n+τk-1),且获取的k阶累积为
ckx(τ1,τ2,…,τk-1)=
cum[x1=x(n),x2=x(n+τ1),…,xk=
x(n+τk-1)]
(5)
ckx为k阶累积量;x(n)为概率密度总量;τ为获取的r阶累积量以及k阶累积数量;τk-1为信号在k-1维的累积数量。最后依据傅里叶变换,对交通信号的双谱进行表示,过程为
(6)
Bx为交通信号中2个频率ω之间的双谱;τ为信号r、k二阶的累积量总和;c3x为3个随机变量的向量和。依据计算结果获取交通信号的双谱。
2.2 交通信号调整
利用卷积神经网络对交通信号进行卷积、池化等进行调整。过程如下:
a.交通信号初始化。将获取的双谱信号进行初始化处理,利用卷积神经网络对双谱信号中的偏置值以及卷积核进行初始化处理,并将信号的偏置值设定为0。
b.卷积。在卷积神经网络的卷积层中输入信号的特征,每个信号的卷积核都参与卷积,卷积核以一定的长度在信号特征中进行移动,并对移动过程进行卷积运算,计算过程为
(7)
l为网络层数;K为卷积核;Mj为感受野;bj为偏置值。
c.信号池化。池化目的是缩减信号特征,通过池化缩减信号检测的计算量,过程为
(8)

(9)
Xl-1为池化后的交通信号特征。
d.光栅化及全连接层。信号特征经过池化后会获取一个系列矩阵,从中获取光栅化后的信号数值向量。将向量输入进卷积神经网络的全连接层,最后经由激活函数构建一个多类别的分类器[10]。过程为
(10)
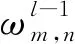
e.调整方向误差。设定信号的输入值为xi,基于上述过程获取预测值,基于输入值与真实值之间的计算,获取信号的损失函数,过程为
(11)
L(xi)为通过计算获取的损失函数;α为学习速率;bi为函数中第i个信号的参数;xi为输入值;y为信号样本W的第i个神经元;∂为神经元系数;bi为最终的信号分类结果。
基于上述计算过程,对移频轨道的交通信号进行分类,实现对移频轨道交通信号的检测。
3 实验分析
为了验证上述交通信号检测方法的整体有效性,需要对此方法进行测试。
分别采用基于时频分析的移频轨道交通信号检测方法(本文方法)、基于无监督学习的卫星NLOS信号检测方法(方法1)以及指数型随机共振微弱振动信号检测方法(方法2)进行测试。
a.随机选定1条移频轨道上的1 000个交通信号,在信号中加入1组随机干扰源,对本文方法、方法1以及方法2的检测精度进行测试,测试结果如图2所示。
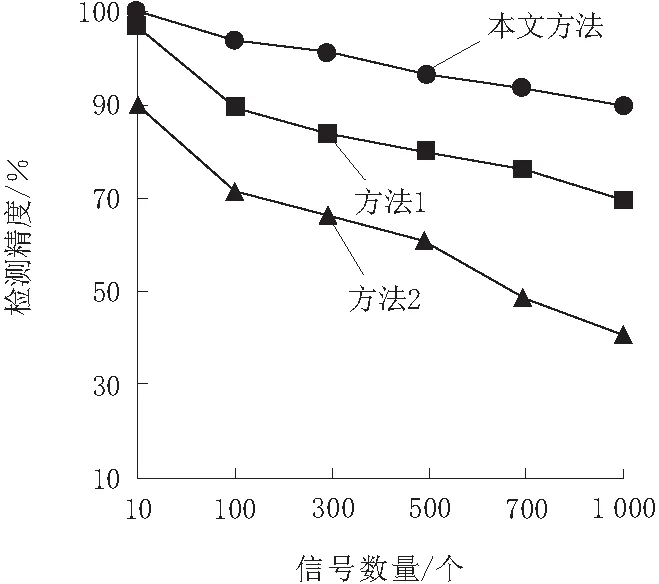
图2 不同方法的检测精度测试结果
依据图2可知,随着信号数量的不断上升,3种信号检测方法的检测精度呈现不同程度下降趋势。方法1在测试初期所测试出的信号检测精度与本文方法不相上下,但随着检测信号数量的增多,检测精度急速下降。方法2的信号检测精度从测试开始就不及本文方法以及方法1,检测精度较差。本文方法在测试初期测试的信号检测精度为100%,虽然测试后期检测精度略有下降,但在随机干扰源影响的前提下,依然能够将检测精度稳定在90%。综上所述,本文方法的信号检测精度要高于方法1以及方法2。
b.基于上述选定的1 000个交通信号,对本文方法、方法1以及方法2的检测误差进行测试,该次测试利用3种方法对信号检测时的频载误差、低频误差以及信号频偏误差进行测试,测试结果如图3所示。
依据图3可知,本文方法在信号检测时测出的误差要低于方法1以及方法2;方法2测试出的误差要高于本文方法,但是对比方法1来看,该方法检测出的误差值要低于方法1;方法1所检测出的误差最大,是3种方法中误差最大的检测方法。从整个测试来看,本文方法的检测误差最低,可以适用于轨道交通信号的检测。
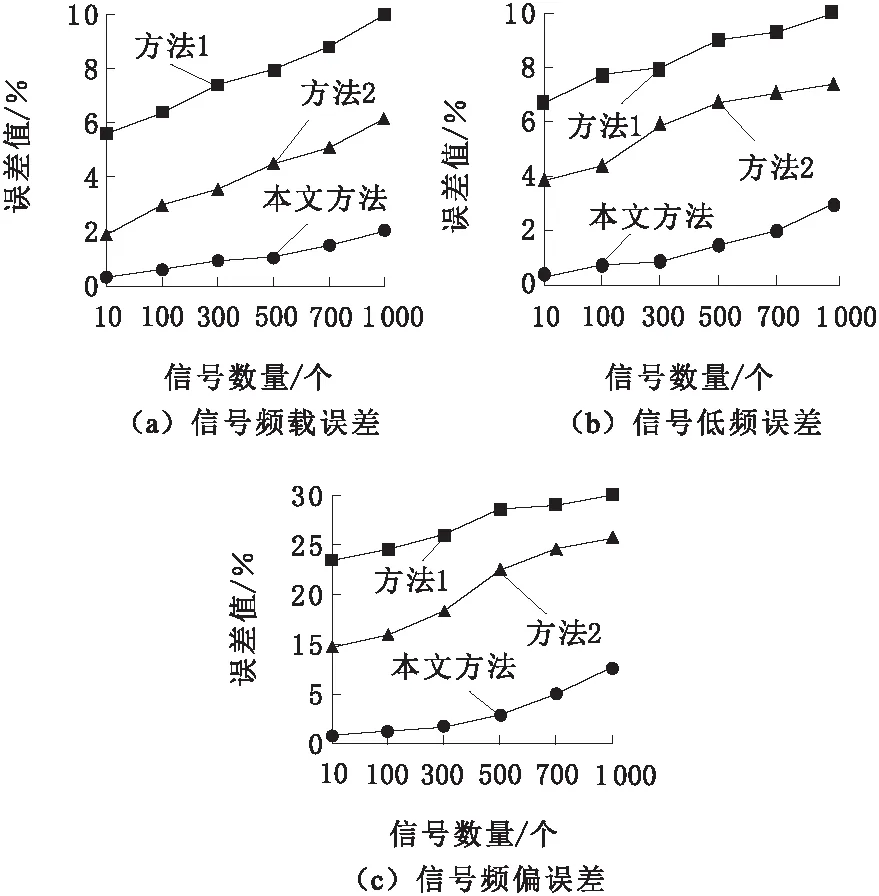
图3 不同方法信号检测的误差对比结果
c.基于上述的实验结果,对本文方法信号去噪前后的噪声频率进行检测,测试结果如图4所示。
分析图4可知,本文方法在去噪前测出的噪声频率较差,而去噪后的噪声频率明显优于去噪前的噪声频率。这主要是因为本文方法在进行交通信号检测前,基于小波去噪方法对信号进行了去噪处理,并利用时频分析法获取了信号的时频特征,所以本文方法在对去噪后的交通信号进行检测时,交通信号的噪声频率稳定。

图4 本文方法去噪前后噪声频率测试结果
4 结束语
随着移频轨道的增多,对移频轨道上的各类信号进行必要检测,成为该行业急需解决的重大难题。针对传统信号检测过程中存在的问题,提出基于时频分析的移频轨道交通信号检测方法。该方法首先利用时频分析法对轨道内的交通信号进行时频特征的提取,再利用卷积神经网络对交通信号进行分类处理,从而实现移频轨道交通信号的检测。由于该检测方法在获取信号时频特征时存在一定缺陷,今后会针对该缺陷进行优化,以此增加该检测方法的准确性。

