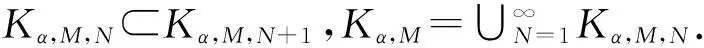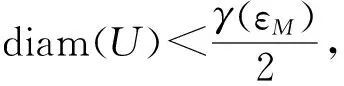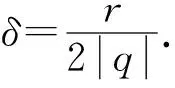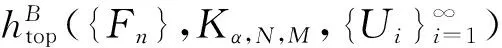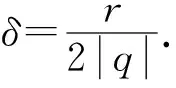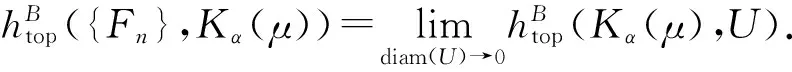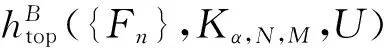Amenable群作用下的局部熵的重分形分析

王 威，曹 洁

(1.南通理工学院 基础教学学院，江苏 南通 226002;2.南京师范大学 数学科学学院，江苏 南京 210023)

重分形分析是动力系统维数理论中一个主要研究内容,现主要推广为两个部分:重分形谱和集合上的维数性质.20世纪以来有较多研究,如文献[1-3],分别在Gibbs测度下和具有Specification性质的扩张同胚上对局部熵和加权熵等问题进行了重分形研究.文献[4-5]也在局部熵的重分形上进行了研究,并获得了较好的结果.设(X,d,T)是动力系统,其中(X,d)是紧致度量空间,T:X→X是连续映射，M(X)为所有弱*拓扑条件下概率测度.记M(X,T)为所有T-不变测度,显然M(X,T)⊂M(X), 重分形分析研究Borel测度μ的点态维数.令

其中:B(x,ε)是x开ε-领域.定义集合

Xα:={x∈X:dμ(x)=α}.

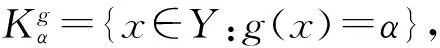
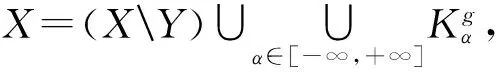
其中：g可以定义Birkhoff平均值、Lyapunov指数、点态维数或者局部熵,G可以定义拓扑熵、拓扑压或者Hausdorff维数.固定q∈和μ∈M(X)，文献[12]定义了广义的Hausdorff维数并且建立了纲量关系式.在文献[13]中, Olsen在d中利用分离条件研究了自仿重分形分析.

设(X,G)是G-作用下的拓扑动力系统,X是带有度量d的紧致度量空间，G是拓扑群，以下假设G是可数离散amenable群.群G是amenable的,如果它含有左不变平均值，即存在G的有限序列子集{Fn}是渐进不变的,亦即

这样的序列称为Følner序列，详情见文献[14].

下面定义(X,G)的拓扑熵.设U是X的开覆盖,U的拓扑熵定义为

其中：UFn=∨g∈Fng-1U.可见htop(G,U)不依赖Følner序列{Fn}的选择，(X,G)的拓扑熵定义为

其中：上确界取遍X的所有开覆盖.

文献[15]在Hausdorff维数的启发下定义了子集上的拓扑熵.在amenable群作用下的动力系统(X,G),利用下列方法定义Bowen熵.

设{Fn}是G的Følner序列,U是X的有限开覆盖.记diam(U):=max{diam(u):u∈U}.对n≥1，用WFn(U)表示集族V={ug}g∈Fn,ug∈U.若V∈WFn(U)，整数m(V)=|Fn|称为V的长度.定义

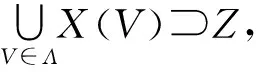
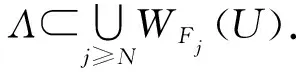
则

定义

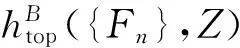
Z作用下子集Bowen拓扑熵也有类似定义，文献[10]证明了

可见Bowen拓扑熵定义有替代方法.

1 相关定义和引理

定义1若Z⊆X,s≥0,N∈，{Fn}是G中的Følner序列，ε>0,定义

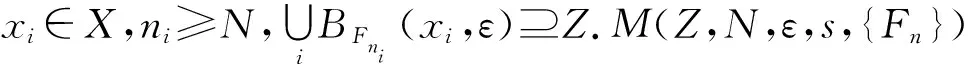
定义2设(X,G)是G-作用紧致度量拓扑动力系统,G是可数离散amenable群.∀μ∈M(X),x∈X,n∈,ε>0,{Fn}是G的Følner序列, 定义

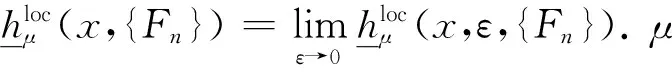
若α≥0,μ∈M(X,T),定义集合

htop(Kα(μ))=qα+hμ(T,q,Kα(μ))，

等式左侧为拓扑熵.

下面研究amenable群作用下的局部熵及其谱,并讨论Kα的大小.设μ为不变非原子测度.不失一般性，假设在任意非空开集上μ是正的.对任意至多可数集r={BFn(x,ε)}，∀q,t∈，令Fμ(r,q,t)=为r的自由能量,记为(r,q,t).对任意给定的非空集合Z⊂X,∀q,t∈,ε>0，N∈，令

上确界取遍所有有限或者可数集合r={BFni(xi,ε)},其中xi∈Z,ni≥N，且满足

再假定Mμ,c(φ,q,t,ε,N)=0.

对任意的q,t,ε,N,量Mμ,c(Zq,t,ε,N)对N是不减的,因此下面的极限存在

下面描述一些性质，这些都是Hausdorfff维数类型的标准证明,类似于文献[15]中的拓扑熵性质及文献[16]中的拓扑压力性质.

引理1∀t∈,Mμ(Z,q,t,ε)具有如下性质:

(1)Mμ(Ø,q,t,ε)=0;

(2)∀Z1⊂Z2,都有Mμ(Z1,q,t,ε)≤Mμ(Z2,q,t,ε)；

注1易证Mμ(·,q,t,ε)是一个外测度.

引理2存在临界值hμ({Fn},q,Z,ε)∈[-∞,∞],满足

引理3下列结果成立:

(1)hμ({Fn},q,φ,ε)=-∞；

(2)∀Z1⊂Z2，都有hμ({Fn},q,Z1,ε)≤hμ({Fn},q,Z2,ε);

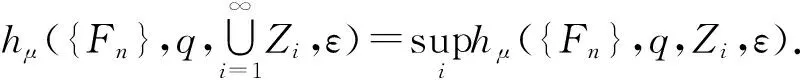
性质1下列结果成立:

(1)hμ({Fn},q,φ)=-∞；

(2)∀Z1⊂Z2，都有hμ({Fn},q,Z1)≤hμ({Fn},q,Z2)；

2 主要结果及证明

定理假设μ为任意非空开集上非原子G-不变正测度.对∀α≥0，每个q∈，有

性质2假设μ为任意非空开集上非原子G-不变正测度.对Z⊂X，有

证明如果Z=Ø, 两侧皆为-∞，显然成立.假设Z≠Ø, 现证

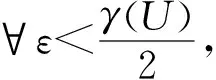
由r的任意性, 考虑如下定义

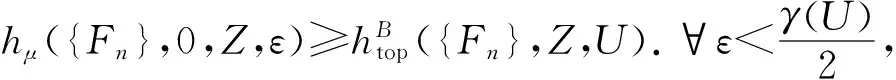
由拓扑熵的定义可知,存在开覆盖U且diam(U)<ε,满足

(1)

设Z′是Z的任意子集，Γ={Uni}是任意弦覆盖Z′的集族.假定对于Uni∈Γ,Uni∩Z′≠Ø.否则,就删除这些弦而获得更小的弦.它们仍然覆盖Z′.∀Uni∈Γ, ∀xUni∈Uni∩Z′.所以xUni∈Uni⊂BFni(xUni,ε).

因此集族γ={BFn(xUni,ε)}是Z′的开覆盖.根据加权自由能量定义, 可得∀s∈,有

Mμ,c(Z′,0,t,ε)≤M(Z′,U,s)，

由M(·,U,s)的单调性可知最后不等式成立，可得hμ({Fn}，0,Z,ε)≥h({Fn},Z,U),与(1)矛盾.

注2若q=0, 由性质1知定理只需证q≠0的情形.

考虑α≥0对应的水平集

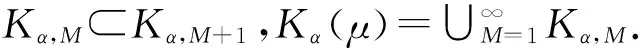
取x∈Kα,M，存在N0=N0(x,δ,εM),满足

∀n≥N0,取

Kα,M,N={x∈Kα,M:N0=N0(x,δ,εM)

引理4设U是X的开覆盖.取M,N∈.考虑集合Kα,M,N满足其中γ(U)是ULebesgue数.那么对于s≥qα+|q|δ+t，可得

M(Kα,N,M,U,s)≤Mμ,c(Kα,N,M,q,t,εM).

证明设n>N,γ={BFni(xi,εM)}是Kα,N,M任意覆盖，且满足xi∈Kα,N,M.对任意i，都有ni≥n≥N.对每个xi，可得某弦覆盖Uni，满足Bni(xi,εM)⊂Uni，即存在Γn={Uni},满足

由于对∀i，都有ni≥n≥N,xi∈Kα,N,M，有

exp(-(α+δ)|Fni|)≤μ(BFni(xi,εM))≤exp(-(α-δ)|Fni|).

如果q≥0,那么μ(BFni(xi,εM))q≥exp(-q(α+δ)|Fni|)，且对s≥qα+qδ+t，有

(2)

另一方面, 如果q≤0,那么μ(BFni(xi,εM))q≥exp(-q(α-δ)|Fni|),且s≥qα-qδ+t，有

(3)

结合(2),(3),得

M(Kα,N,M,U,s,n)≤Mμ,c(Kα,N,M,q,t,εM,n).

令n→∞,有

M(Kα,N,M,U,s)≤Mμ,c(Kα,N,M,q,t,εM).

引理5取M,N∈,考虑集合Kα,M,N,设U是X的开覆盖，满足那么对s≤qα-|q|δ+t,有

Mμ(Kα,N,M,q,t,εM)≤M(Kα,N,M,U,s).

集族BFn(x,εM)是Z的中心覆盖.因为xUni∈Z⊂Kα,N,M且n>N，所以

exp(-(α+δ)|Fni|)≤μ(BFn(xUFni,ε))≤exp(-(α-δ)|Fni|).

若q≥0，有

若s≤qα-qδ+t.由Γn的任意性，有

Mμ，c(Z,q,t,εM,n)≤M(Z,U,s,n).

令n→∞，有

Mμ，c(Z,q,t,εM)≤M(Z,U,s)≤M(Kα,M,N,U,s).

Mμ(Kα,M,N,q,t,εM)≤M(Kα,M,N,U,s).

(4)

若q≤0，有

μ(BFni(xUni,εM))q≤exp(-q(α+δ)|Fni|).

因此，有

对s≤qα+qδ+t, 类似于q≥0，有

Mμ(Kα,M,N,q,t,εM)≤M(Kα,M,N,U,s).

(5)

结合(4)，(5)得证.

下面完成定理的证明.根据 Bowen拓扑熵的定义需证

假设Kα(μ)≠Ø.否则,由于等式两边都趋于-∞,显然成立.当Kα(μ)≠Ø时，证明分两步.

假设不成立，取

(6)

因为

且

由s=qα+hμ({Fn},q,Kα(μ))+2r，t=hμ({Fn},q,Kα(μ))+r-|q|δ和引理4,有

(7)

与假设矛盾.事实上

hμ({Fn},q,Kα(μ),εM)≥hμ({Fn},q,Kα,M,N,εM)，

所以，有

Mμ(Kα,N,M,q,hμ(T1,q,Kα(μ))+r-|q|δ,εM)=0，

与(7)矛盾.

假设不成立.取

qα+hμ({Fn},q,Kα(μ))>h({Fn},Kα(μ),U)+3r.

下列表达式成立

(8)

当M,N充分大，这是可能的，因为

M(Kα,N,M,U,qα+hμ({Fn},q,Kα(μ)-2r))=0.

由s=qα+hμ(T,q,Kα(μ))-2r，t=hμ({Fn},q,Kα(μ))-r+|q|δ和引理5，有

Mμ(Kα,N,M,q,hμ({Fn},q,Kα(μ))-r+|q|δ,εM)=0，

(9)

与假设矛盾, 事实上

hμ({Fn},q,Kα(μ),εM)-r≤hμ({Fn},q,Kα,M,N,εM)，

所以，有

Mμ(Kα,N,M,q,hμ(T1,q,Kα(μ))-r+|q|δ,εM)=∞，

与(9)矛盾.

根据(i),(ii)，知定理成立.