针对新型冠状病毒肺炎隔离措施的动力学评估

刘 芳，张 娟，杨 红

(1.忻州师范学院 数学系，山西 忻州 034000；2.山西大学 复杂系统研究所，山西 太原 030006)

2019年底暴发的新型冠状病毒(COVID-19)肺炎在全球人群中快速传播，已造成世界性大流行.至2020年7月底，全球确诊人数达1.7×107，死亡人数达6.7×105.此新型冠状病毒，主要通过飞沫传播和接触传播，并且感染者在潜伏期具有一定的传染性.其感染性极强，传播速度极快.在暴发初期,中国受到春运、交通、环境、舆情等多种因素的影响，面临着巨大的挑战和压力.自疫情暴发以来，全国各省市出台了一系列强有力的防控政策和措施.2020年1月23日，武汉启动公共卫生一级响应，采取限制交通、居家隔离、集中收治等措施，进一步阻断家庭与社区传播.与此同时，中国政府在全国范围内采取居家隔离、人口普查与追踪等措施来预防和控制全国疫情的传播，取得了显著成效.目前，有大量文献针对湖北省疫情[1-7]及湖北以外地区进行疫情分析[8-11].

在中国所采取的一系列防控措施中，普通民众的居家隔离与对确诊患者密切接触者的追踪隔离政策，切断了传播路径，在病毒传播控制中起到了关键的作用.论文建立新型冠状病毒传播与控制动力学模型，定量评估这两项隔离措施对疫情的影响.针对此模型，分析其动力学特征，给出基本再生数与有效再生数表达式.利用安徽省公开报道数据，对模型进行数值模拟，估计模型参数与初值及其置信区间，对比有隔离措施与无隔离措施对疫情传播的影响.通过参数对基本再生数、有效再生数的敏感性分析，定量评估控制措施的有效性，讨论隔离措施在疫情下的防控效果.

1 数学模型与动力学分析

根据新型冠状病毒在人群中的传播发展规律，基于中国当前防控措施及传染病动力学研究[12-18]，建立新型冠状病毒传播与控制动力学数学模型.

1.1 动力学模型

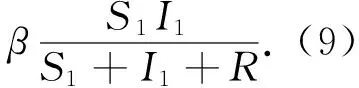
基于以上假设，论文绘制了以下传输过程示意图(如图1所示)，用来描述新型冠状病毒在人群中的传播过程，其中箭头表示个体在仓室之间的移动.

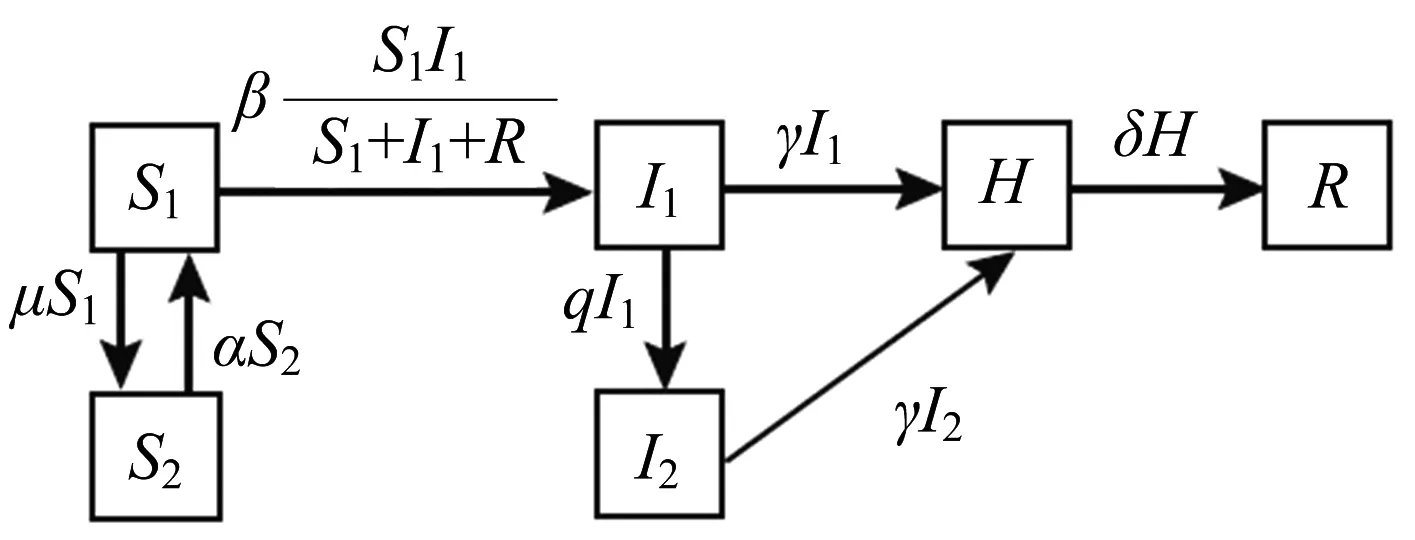
图1 COVID-19传输过程示意图

基于新冠肺炎疾病传播过程示意图，建立了传染病动力学模型，见式(1).

(1)

其中：α,β,γ,δ,μ>0.

令N=S1(0)+S2(0)+I1(0)+I2(0)+H(0)+R(0)，由模型(1)，易得若S1(0),S2(0),I1(0),I2(0),H(0),R(0)≥0，则系统(1)的正不变集为D={(S1,S2,I1,I2,H,R):0≤S1,S2,I1,I2,H,R≤N}.

1.2 动力学分析

1.2.1 极限集

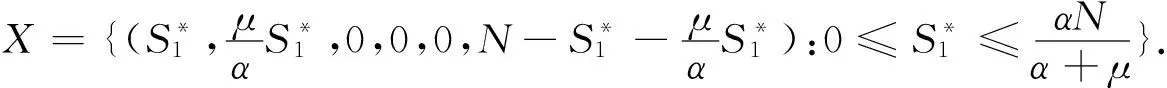
证明基于系统(1)得到下列公式

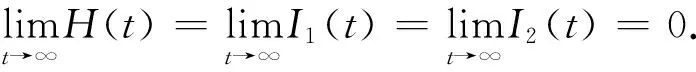
其中：S1(t)+S2(t)=N-R*.

计算得

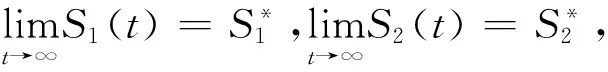
1.2.2 基本再生数与有效再生数

随着新冠疫情的控制，需要利用有效再生数来刻画在疾病传播过程中每个时刻一个染病者在其病程内平均传播的患者数.有效再生数是病毒传播是否能够维持的重要指标，它不仅可以反映外部干预措施的有效性和判断传染病疫情的走势，也可作为传染病风险管理政策的有力参考.

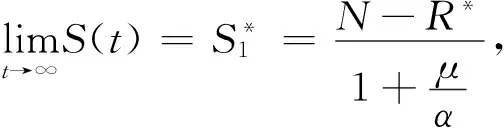
得到

1.2.3 局部稳定性

(2)

解得它的特征值为

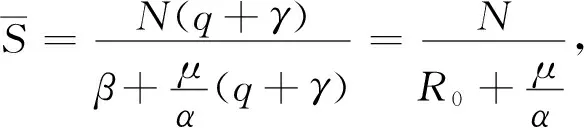
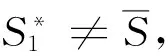
(i)P*总有一个1维中心流形；

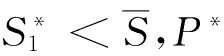
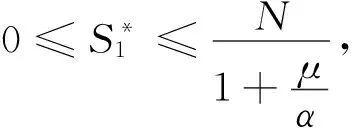
推论令P*∈P0，对于系统(2)，当R0<1时，P*总有1维中心流形和4维稳定的局部流形.

1.3 无隔离项的模型

若没有隔离政策，取α=0,μ=0,q=0，则建立无隔离项的传染病模型为

(3)

2 数值仿真

数据说明：论文以安徽省累计病例数据作为分析对象，分析隔离措施的实施对疫情控制的影响.在疫情早期阶段，武汉“封城”政策前的人员外流对全国疫情的扩散具有较大影响.2020年1月23日武汉封城，2020年4月8日，武汉市解除离汉离鄂通道管控措施，有序恢复对外交通.论文选择2020 年1月30日至2020年4月8日为研究时间区间，不考虑人员流动且总人口为常数.

基于安徽省累计确诊病例数，利用MCMC(Markov chain Monte Carlo)方法，对模型(1)进行初值与参数估计，并给出其95%的置信区间.初值与参数的数据说明如表1所示.

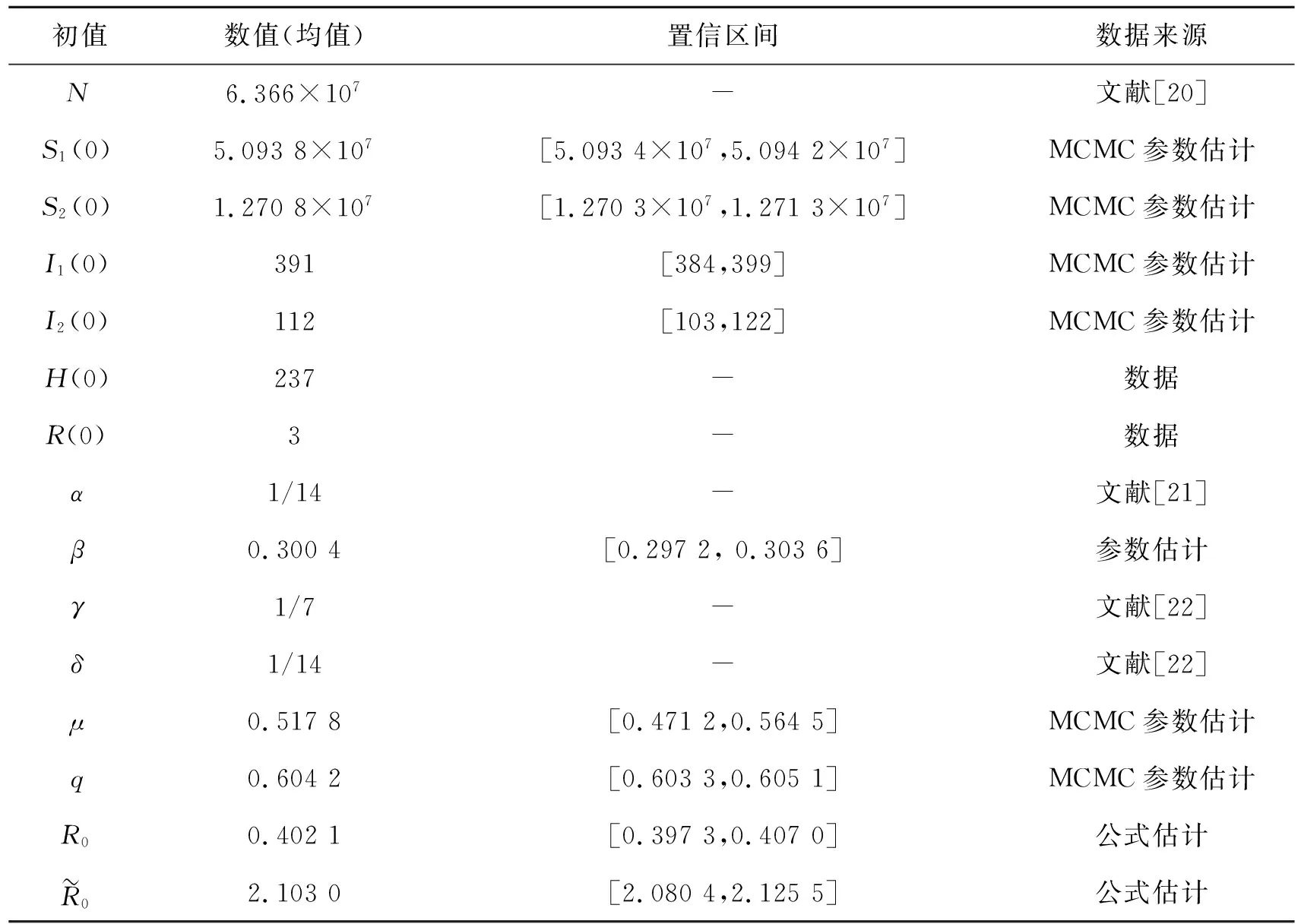
表1 初值与参数说明

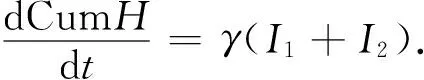
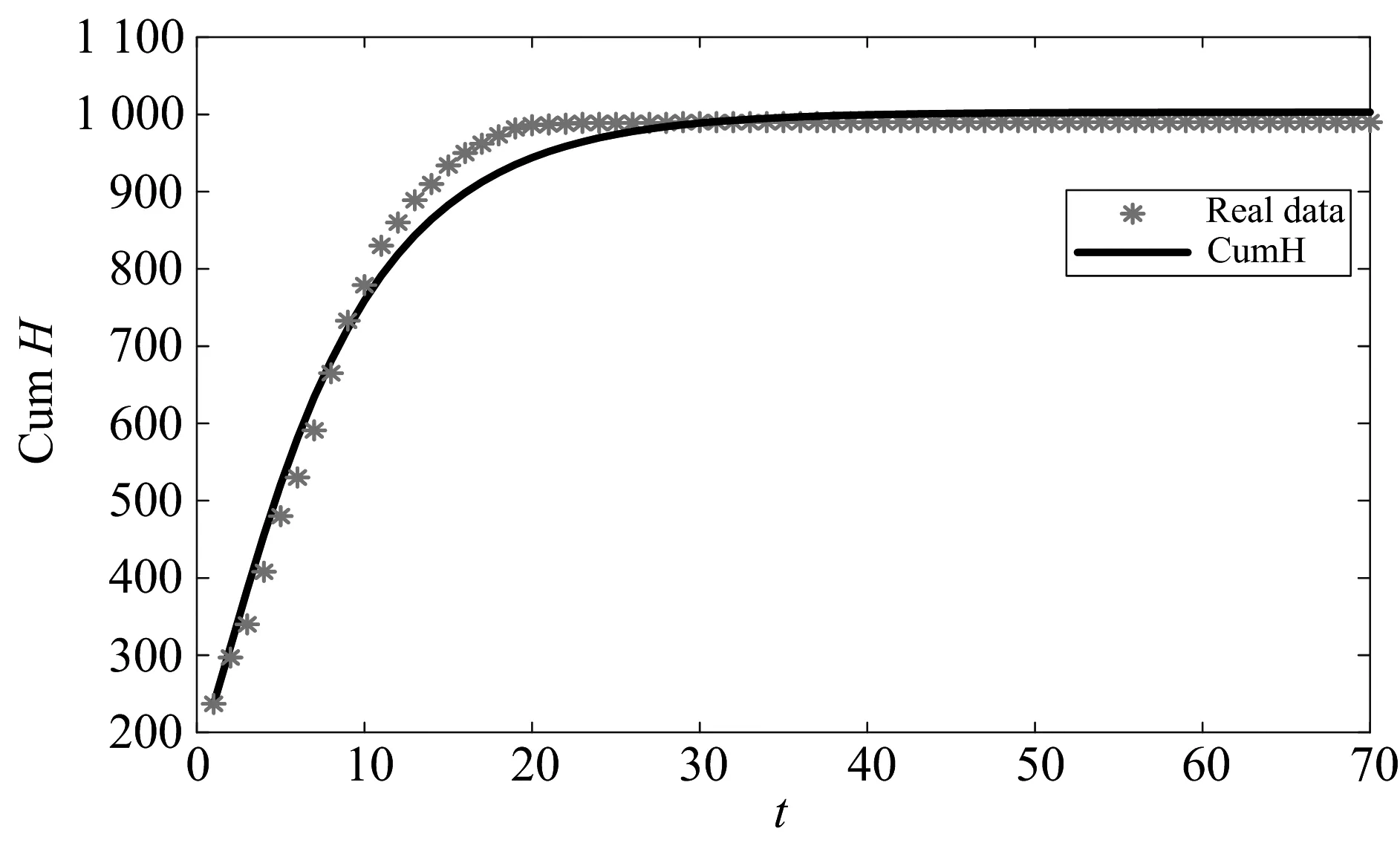
图2 模型(1)与累计确诊病例数的拟合曲线

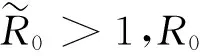
图3为参数对基本再生数的影响，验证了基本再生数R0与传染率系数β正相关，传染率系数β越大，基本再生数R0越大.基本再生数R0与染病者的隔离速率系数q(或确诊速率系数γ)负相关，隔离速率系数q(或确诊速率系数γ)越大，基本再生数R0越小，说明了加强密切跟踪隔离力度，即增加染病者的隔离速率系数q，能够有效降低基本再生数R0.

图3 参数对基本再生数的影响

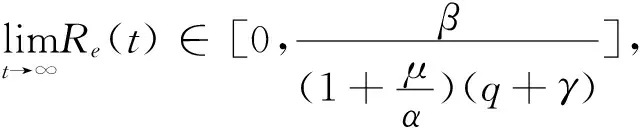
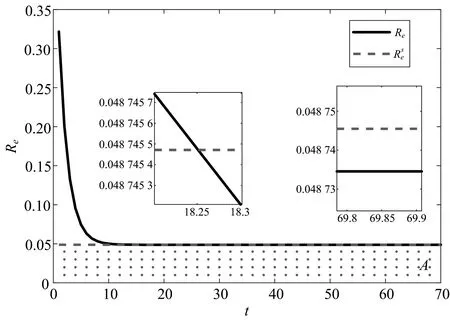
图4 有效再生数的时间序列图

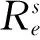
3 结束语

通过对基本再生数与有效再生数的分析，加强密切跟踪隔离力度，即增加染病者的隔离速率系数，能够有效降低基本再生数；加强居家隔离力度，即增加易感者的隔离速率系数与减少易感者的隔离解除速率系数，有助于降低有效再生数极限范围的上限.说明隔离措施的实施确实能够有效控制疫情传播规模.与此同时，当身体异常如高温、咳嗽等症状及时前往医院治疗，缩短确诊时间，同样可以减少基本再生数，对疫情防控起着积极作用.模型没有考虑人口流动对疫情传播的影响，特别是武汉解封之后的人口流动导致人口的流入流出以及国外的输入性病例对各个地区疫情的影响.在论文研究基础上，下一步作者将分析各地区的人口流动与输入性病例对新冠肺炎流行性传染病的影响.