基于三参数有理函数的长期沉降预测模型
赵 宏,戈海玉,杨富莲,周 明,葛清蕴
(皖西学院 建筑与土木工程学院,安徽 六安 237012)
随着国家高速铁路的飞速发展,高速铁路路堤式道路的工后长期沉降问题也越来越引起人们的关注,路基的工后沉降问题属于道路的变形特性,路基土的动力本构关系复杂,虽然目前研究较多,但仍未有较好的预测长期沉降的模型。常用计算模型基本分为两类:一类是基于复杂的动力弹塑性本构模型例如多屈服面模型[1]和边界面模型[2-4]。Prévost[1]提出了多屈服面的模型计算土体的循环荷载下的土体应变模型。但是多屈服面模型在有限元程序中实现过程繁琐,且对计算机内存存储量要求较大。柳军修等[2]基于FLAC3D软件开发了结构性黏土边界面模型。边界面模型参数获取不容易,而且计算量较大。另外一类是基于经验拟合的简化模型[5-14],其中应用最广泛的是Monismith的指数模型[8]。Li和Selig[9]将累积塑性应变表示为循环次数的函数,考虑了动偏应力的影响。C Chen[10]基于Cam-clay本构模型研究了泥炭有机土的累积塑性应变特性。X W Ren等[11]还对软质海相黏土饱和土在长期低循环载荷下的孔压特性进行了研究,提出了新的孔隙压力模型,并通过三轴试验进行了验证。除了指数模型,对数模型也是比较常见的计算软土地基的循环累计应变的模型,PARR[12]提出了对数的循环累积变形模型。此外经验公式还有双曲线模型[13-14]。
由于双曲线模型在拟合长期沉降规律上比较符合长期沉降的规律,通过试验获取参数也较容易,所以应用也比较多,但是传统的双曲线预测模型在荷载作用次数比较少的时候误差较大,因此本文在传统的双曲线预测模型上增加一个线性项,即采用三个参数的有理函数的预测模型。
1 计算模型
1.1 土体长期沉降模型
常用的软土地基长期沉降预测模型大多采用的是在Monismith基础上发展起来的指数预测模型,但是指数预测模型在荷载作用次数很大时候,土体的累积变形是趋向无穷大的,但是实际这种情况是不可能的,因此我们采用张鹏军[13]、王元战[14]的双曲模型。张鹏军采用的是王元战的循环累积应变模型[14],虽然克服了指数模型的缺点,但在循环荷载比较小的情况下误差较大,如图1所示。图1是在静偏应力qs=0和动偏应力qd=50kPa时候的实验数据,从图中可以看出采用王元战模型(公式1)拟合模型得到的精度较差,拟合相关度只有R2=0.7693。
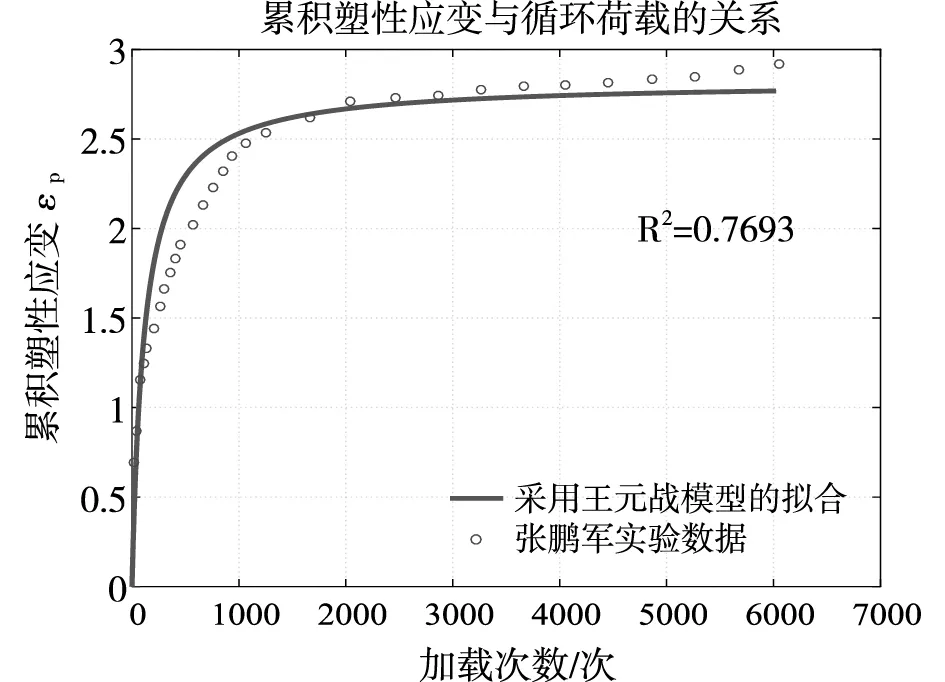
图1 文献13的实验数据模型(qs=0;qd=50kPa)
(1)
其中,εp为累积循环应变,N为循环作用次数,其中a,b为系数,与静偏应力qs,动偏应力qd,围压pc有关。
由式(1)可知,当N较大时候,累积应变逼近于常数a,也就是说应变幅值取决于常数a;而曲线上升快慢取决于常数b;在循环荷载较小时候,累积应变在循环荷载量较小时候,拟增加一项,即在公式(1)的基础上增加一个常数项,可以逼近在循环荷载较小时候的拟合精度,因此可以写成:
(2)
把式(2)简化整理,可以写成式(3)有理函数形式,本文采用式(3)所示的累积循环应变模型。
(3)
其中a=f(qs,qd,pc),b=f(qs,qd,pc),c=f(qs,qd,pc),可以通过实验数据得到a,b,c和静偏应力qs,动偏应力qd,围压pc的关系。
1.2 循环累积变形模型中系数的确定
1.2.1 系数的确定
本文软土采用深圳前海的软土模型,数据取自文献[13],在不同静偏应力qs,动偏应力qd下进行了三轴试验,本文对文献[13]的实验数据采用公式(3)的软土长期沉降模型,进行了拟合,并对参数a,b,c进行了统计确定,得到参数a,b,c反映与静偏应力qs,动偏应力qd的关系。实验数据拟合得到的参数a,b,c数据见表1。
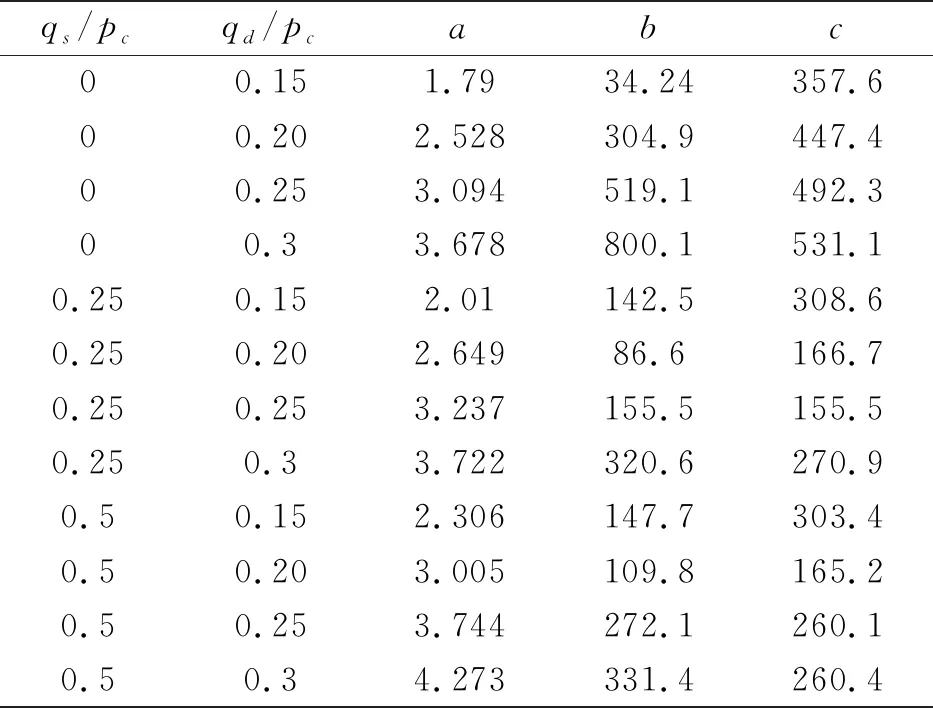
表1 对公式(3)拟合得到的系数a,b,c
1.2.2 系数与静偏应力qs,动偏应力qd的关系
为了研究三参数有理函数模型中参数a和静偏应力qs,动偏应力qd的关系,把表1中a和静偏应力qs,动偏应力qd的数据绘成如图2所示的函数曲线。
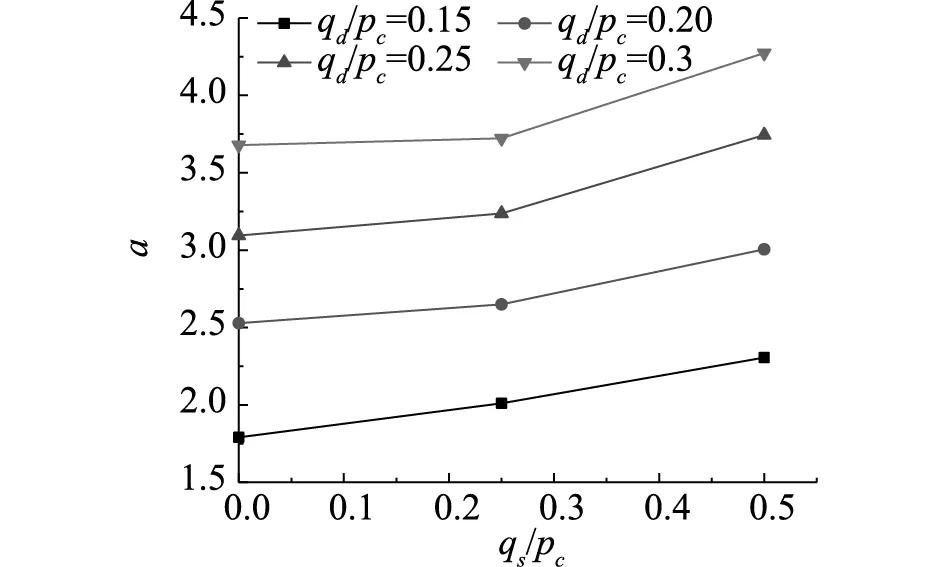
(a)a与qs的关系
通过图2可以看出a和静偏应力qs,动偏应力qd的关系都近似成线性关系。因此通过拟合可以得到a和静偏应力qs,动偏应力qd的关系见公式(5),拟合得到的图形,如图3所示。从图3中可以看出a和静偏应力qs,动偏应力qd都是线性关系。
图3 系数a与qs和qd的关系(R2=0.9841)
(5)
系数b与静偏应力qs和动偏应力qd的关系,如图4所示。
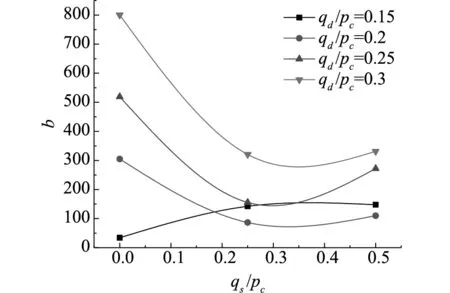
(a)b与qs的关系
从图4中可以看出b与qs和qd近似成非线性关系,b与qs和qd关系可以近似用三次多项式来表示,可以表示成公式(6)形式。
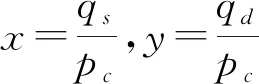
b=k1x2y+k2xy2+k3x2+k4y2+k5x+k6y+m
(6)
对公式(6)进行拟合得到公式(7)中的系数,得到b和qs和qd拟合关系可以用公式(7)表示拟合的图形,如图5所示。
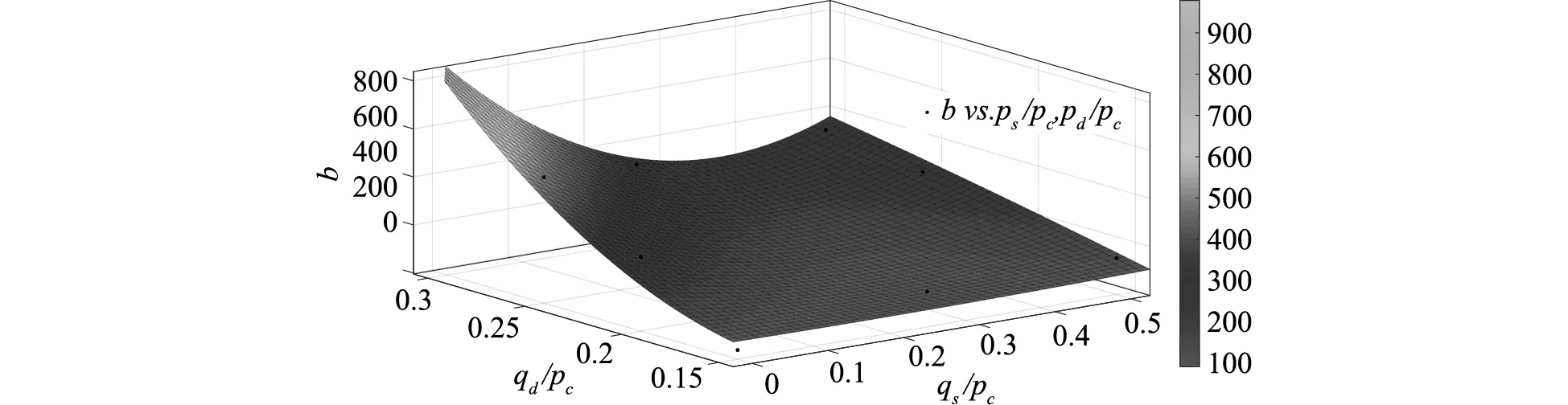
图5 系数b与qs和qd的关系(R2=0.9542)
b=25750x2y-44000xy2-3577x2+21950y2+857.2x-5059y+372.9
(7)
同理,系数c与静偏应力qs和动偏应力qd的关系,也可以按照系数a,b的确定方法进行确定,如图6所示。

(a)c与qs的关系
从图6中可以看出c与qs和qd近似成非线性关系,qd与qs可以近似用二次多项式来逼近,c与qd近似用三次多项式来表示。
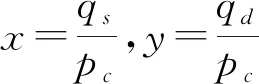
c=k1x2y3+k2xy3+k3y3+k4x2y+k5y2+k6xy2+k7x2+k8x+k9y+m
(8)
通过拟合可以得到公式(8)中的各项系数,拟合度R2=0.9584,如图7所示。

图7 系数c与qs和qd的关系(R2=0.9584)
1.2.3 循环累积变形模型
将公式(5)、(7)、(8)代入公式(3)即可得到考虑动偏应力、静偏应力的深圳前海地区的软土长期沉降应变模型。
2 模型验证
为了验证本文模型的正确性,本文采用文献[13]中数据进行验证。图8为采用本文模型在qs=0,qd=50kPa时候的模型数据与张鹏军的实验数据[13]的比较,可以看出拟合效果较好,尤其在加载次数较小时候,精度更高。
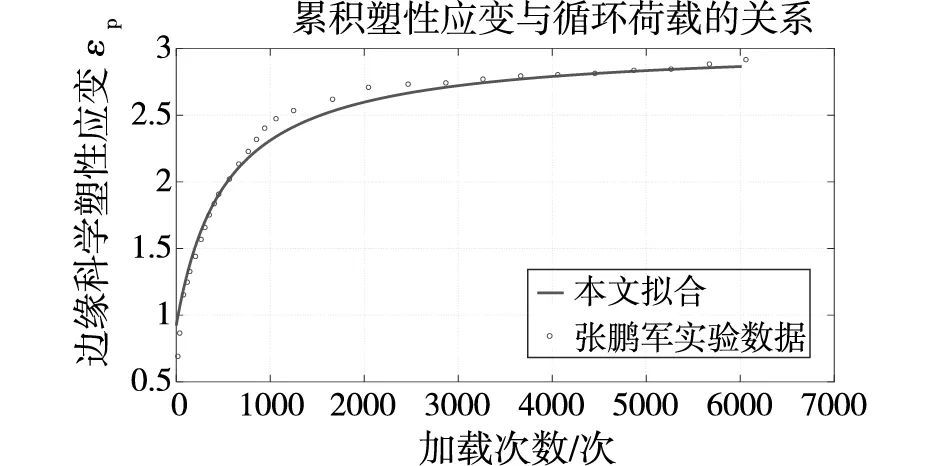
图8 累积塑性应变与循环荷载(qs=0;qd=50kPa)
3 沉降计算
计算模型采用分层总和法计算软土地基的沉降,分层计算每层地基土体的累积沉降。分层计算公式见公式(9)。
εp=∑εpihi
(9)
其中εp为累积总沉降,εpi为第i层土的累积沉降量,hi为第i层土的厚度。
3.1 求地基中动偏应力、静偏偏应力
通过有限差分软件FLAC3d建立路基模型,如图9所示,路基模型包括轨道、道砟层,黏土层、路基组成。然后通过建立荷载模型,分别计算自重作用下和列车动荷载作用下路基不同深度处的应力,进而计算出分层地基的静偏应力、动偏应力。动偏应力的计算公式采用公式(10)进行计算。计算模型采用动力吸收边界。

图9 flac3d建立的路基模型
(10)
3.2 计算分层地基的累积沉降
路基模型的沉降主要是软土地基沉降,道砟沉降量很少,因此本文计算不考虑道砟沉降的计算,主要探讨软土路基沉降。利用公式(9)计算分层地基的沉降。
3.3 循环荷载下累积沉降规律
路基模型采用深圳前海隧道地区的软土模型,计算得到软土沉降随循环荷载增大的沉降规律,如图10所示。从图10中可以看出,软土沉降量随着荷载次数增加,沉降急剧增加,但是增加到5000次以后沉降量趋于稳定不再继续增加。
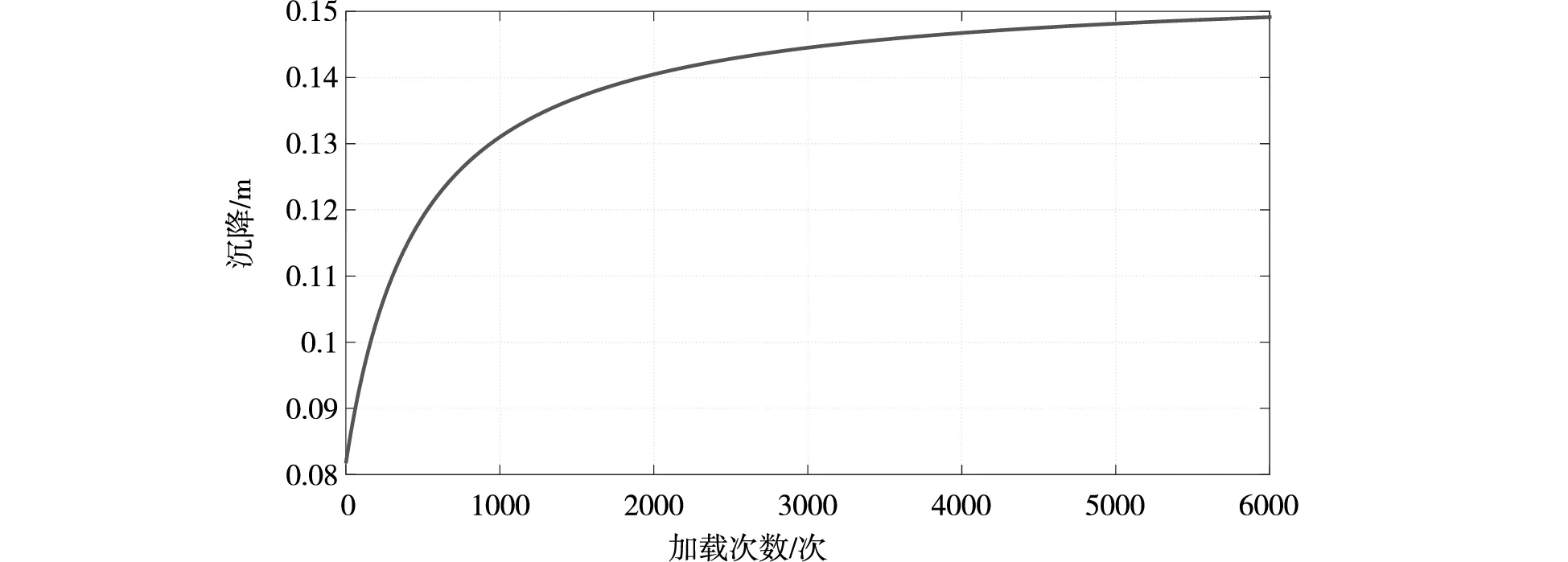
图10 软土随加载次数的长期沉降规律
4 结论
(1)通过有理函数模型y=(ax+b)/(x+c)三参数模型可以很好地反映软土地基的长期沉降,通过模型分析得到三参数模型与传统的双曲线模型相比,可以在循环荷载次数较小的时候获得更好的预测精度。
(2)模型中的参数都是静偏应力和动偏应力的函数,可以通过已有的三轴试验数据多元函数回归分析获得参数与静偏应力和动偏应力的函数关系,参数获取也比较容易。
(3)通过有理函数模型可以通过建立数值模型,并结合分层总和法计算地基的长期沉降,计算结论可靠。

