新型模块化多电平换流器的设计与应用

于 飞，王子豪，刘喜梅

新型模块化多电平换流器的设计与应用

于 飞，王子豪，刘喜梅

(青岛科技大学自动化与电子工程学院，山东 青岛 266061)

随着电力系统电压等级的不断升高，模块化多电平换流器(Modular Multilevel Converter, MMC)桥臂中串联的子模块数量增多，硬件成本升高，制约了其在直流输电系统中的发展。针对这些问题，通过分析多电平换流器和现有的阶调式模块化多电平变换器(Gradationally Controlled Modular Multilevel Converter, GC-MMC)的工作原理，提出了一种新型的换流器。为了解决新型逆变器的电容电压平衡问题，提出了一种适用于新型逆变器的新型稳压算法。最后在Matlab/Simulink环境下搭建了双端标幺值控制的柔性直流输电系统，将新型逆变器应用于系统中进行了验证。仿真结果表明，新型换流器输出电平数量比普通MMC多，输出交流侧和直流侧的波形质量达到直流输电要求。通过对新型逆变器和普通MMC分别进行成本计算，结果表明新型逆变器的建设成本大大少于普通MMC。

模块化多电平换流器；阶调式多电平逆变器；阶调式模块化多电平变换器；电容电压平衡算法

0 引言

随着电力系统的不断发展，电力系统的规模也在不断扩大，直流输电[1-3]已经成为我国电力输电的重要组成部分。在中国快速发展的背景下，城市面临着电力系统发展迟缓、供电走廊紧缺等诸多问题。而高压直流输电(High Voltage Direct Current, HVDC)在解决这些问题时表现出显著的优势[4-7]。模块开关损耗小，有功无功可以分开控制，可为孤岛系统供电，无需无功补偿设备等[8-11]。但是换流站建造成本高、系统结构复杂[12]，对子模块的电容均压算法要求较高[13-15]，这些问题限制了柔性直流输电技术在我国的发展。

文献[16]介绍了现有GC-MMC的调制方法和电路拓扑，并介绍了一种稳压方法。控制相单元中4个子模块产生不同的输出电压c、2c、4c和8c，用穷举法列出了子模块的所有68种组合情况，使每个相单元可以产生15阶电平输出电压，并将其应用于光伏系统中进行验证。这种稳压方式在15阶电平、4个子模块的情况下，就组合出了68种方式。而高压输电桥臂子模块的数量很多，穷举法的稳压方法无法实现。文献[17]提出了一种电压降落的补偿装置，由具有分级输出电压的逆变装置串联组成，分级电压比例为2倍，能够在电压下降时补偿电压。文献[18]根据阶调控制策略，提出了一种基于两种类型功率器件的MOSFET和IGBT混合级联逆变器。每个桥臂由三个H桥单元串联组成，低电压电桥由MOSFET组成，高压电桥由IGBT组成，每个H桥单元的直流电压满足1:2:4的比例关系。

上述所有文献提出的模型都只能产生数量较少的电平，无法应用于高压输电。为解决这一问题，结合现有的GC-MMC和普通的MMC，本文提出了新型的多模块阶调式模块化多电平换流器(Multi-modular Gradationally Controlled Modular Multilevel Converter, MGC-MMC)，并且构建了两端柔性直流输电系统仿真模型。通过对仿真模型的系统运行情况和调制策略进行分析，相较于现有的GC-MMC，能产生更多数量的电平，而且谐波含量少，成本大幅减少，灵活性大大增加。

1 MGC-MMC电路结构

新型MGC-MMC与现有GC-MMC相比，电路拓扑和数学模型相似，区别在于：(1) GC-MMC只能用于低压直流输电，MGC-MMC可以用于中高压；(2) GC-MMC用穷举法稳压，局限性较大；(3) MGC-MMC继承了MMC原有冗余配置的优点，在发生故障时可以通过冗余的子模块提高MGC-MMC的可靠性和灵活性。

本文以新型单相MGC-MMC为例，对电路拓扑进行说明，具体电路结构如图1所示。

MGC-MMC把所有串联在桥臂上的子模块分为三组逆变单元，把三组逆变单元分别定义为1、2和3。三组逆变单元中的子模块电容值之比为1:2:3=4:2:1，因为电容值成比例，所以运行中的电容电压值也成比例，比值为1:2:3=1:2:4。

每组逆变单元由个全桥子模块串联而成，每个全桥子模块又由4个IGBT、4个二极管和1个电容组成，子模块拓扑结构如图1所示。虽然半桥型子模块结构具备损耗小、造价低等优势，但由于反并联二极管可以为故障电流提供通路，存在无法隔离直流故障、不适用于长距离架空线路的问题[19]，所以本文采用全桥结构。

图1 单相MGC-MMC电路拓扑

当桥臂电流正向时，逆变单元中的子模块正投入表示其电容充电，负投入表示电容放电；当桥臂电流反向时，子模块正投入表示其电容放电，子模块负投入则电容充电；子模块切除时，其电容既不充电也不放电。

本文设逆变单元1、2和3中的子模块数量为1、2和3，dc为直流侧直流电压，u为上桥臂输出电压之和，u为下桥臂输出电压之和，1、2和3分别为三个逆变单元输出电压，i和i分别为上下桥臂电流。因为逆变单元中子模块的数量可控，所以MGC-MMC的总输出电平数量为

为了保持直流侧电压恒定，所以上下桥臂投入的所有子模块电压值之和保持恒定，所以直流电压为

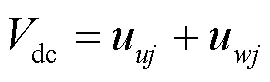
上桥臂输出电压为

下桥臂与上桥臂输出电压计算方法相同。如果计及桥臂电感0，则直流电压计算公式为

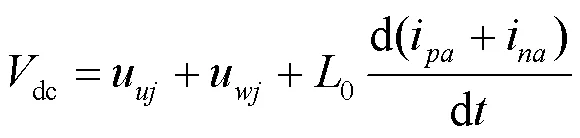
2 MGC-MMC稳压策略

因为NLM调制方法具有良好的跟踪特性，而且在电平数量比较多的情况下谐波含量少[20]，所以本文采用NLM调制法。

因为本文逆变单元之间电压不同，传统的MMC稳压算法无法适用，所以本文提出了基于MGC-MMC的新型稳压算法。因为MGC-MMC的子模块数量少于普通MMC，所以可以通过增加投切次数来保持电容电压稳定，调制波每次阶跃后，GC-MMC包括两轮投切。

2.1一轮投切

首先，把所有的电容电压根据式(5)和图2归算到同一级别，并且根据电容电压的相对大小进行排序。根据电容稳压算法，逆变单元子模块的电压比值1:2:3=1:2:4。

调制波每次阶跃后，如果桥臂电压小于调制要求，需要根据下方所述规则一投入经过归算和排序的电容直至大于调制要求。如果桥臂电压大于调制要求，需要根据下方所述规则一反向投入归算和排序的电容直至小于调制要求(投入和反向投入时按照实际电容电压，归算和排序仅用作比较相对电压大小)。

因为投入和反向投入的电容顺序是归算和排序后的，所以超过和小于调制要求的电压差随机。本文以调制波向上阶跃，需要投入电容为例进行说明。当调制波向上阶跃1，因为所有电容根据电压进行排序，投入的电容可能属于任何一个逆变单元，所以超过的部分随机。虽然随机，但是总共有四种可能，分别为1、2、3和4。所以还需要一个等效电容进行二轮投切以满足调制要求。一轮调制过程中，桥臂电压和调制要求之间的关系如图3所示。

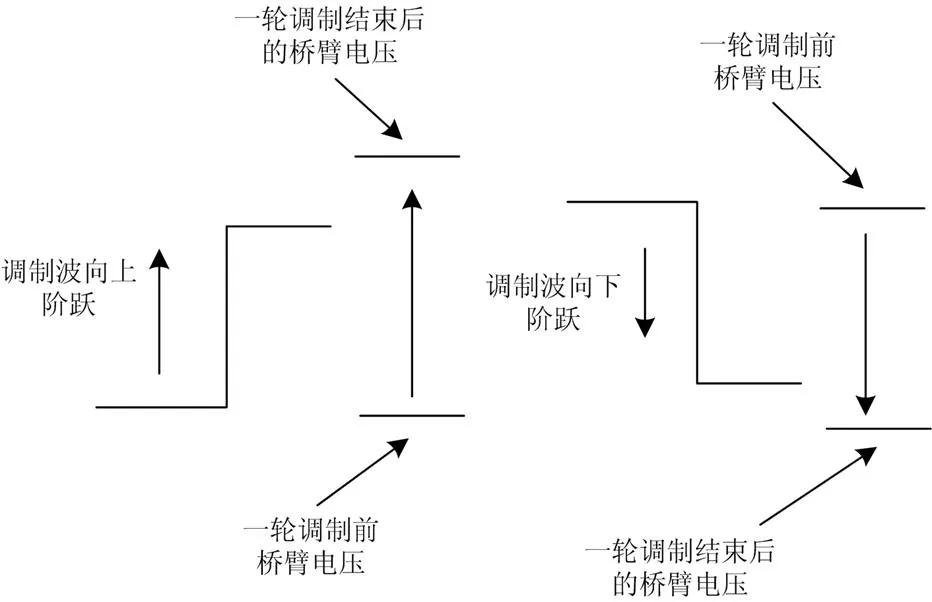
图3 一轮调制过程中电压关系

2.2 二轮投切

一轮调制结束后，如果桥臂电压大于调制要求，需要反向投入电容至调制要求，如果桥臂电压小于调制要求，需要投入电容至调制要求。二轮调制过程如图4所示。

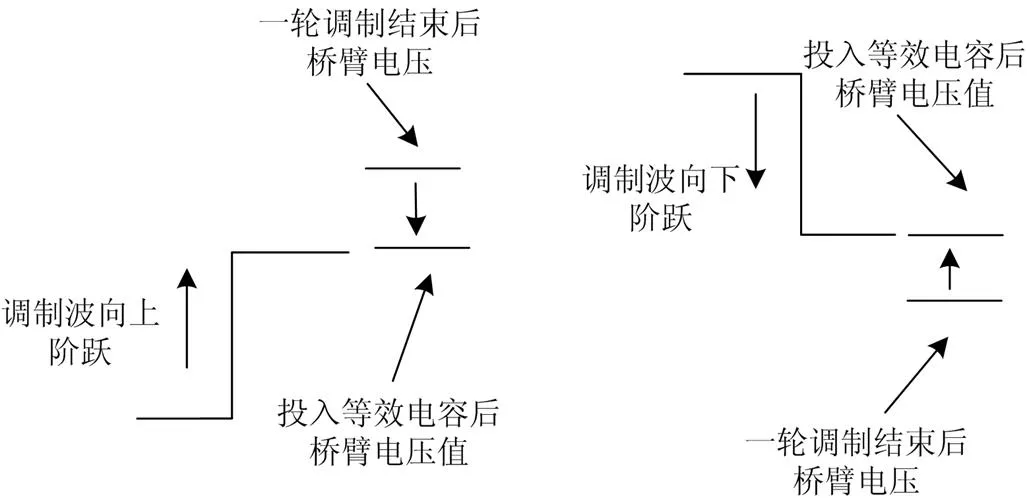
图4 等效电容示意图

因为桥臂输出电压是三组逆变单元所有子模块的输出电压之和，所以可以用数学组合的方式组成等效电容。根据下方所述规则一和规则二即可确定组成等效电容的具体电容，只有当桥臂电压满足调制要求时，才会进行下一步操作。本文以调制波向下阶跃，一轮调制结束后调制要求电压大于桥臂电压一阶电平，需要投入电容为例，对等效电容进行说明，对应于图4右侧情况。

因为此时调制要求高于桥臂电压一阶电平，可以选择投入逆变单元1中的一个子模块。如果1中的子模块已经全部正投入，可以正向投入一个2中的子模块，同时反向投入一个1中的一个子模块，相当于2-1。如果逆变单元1和2的所有子模块已经全部正向投入，选择正向投入一个3中的子模块，同时分别反向投入一个1和2的子模块，相当于4-1-2，或者选择反向投入三个1中的子模块，相当于4-1-1-1。此时不仅满足了调制要求，还使反向投入的电容可以参与下一次调制波阶跃后的投切。上述等效电容的组成过程如图5所示。

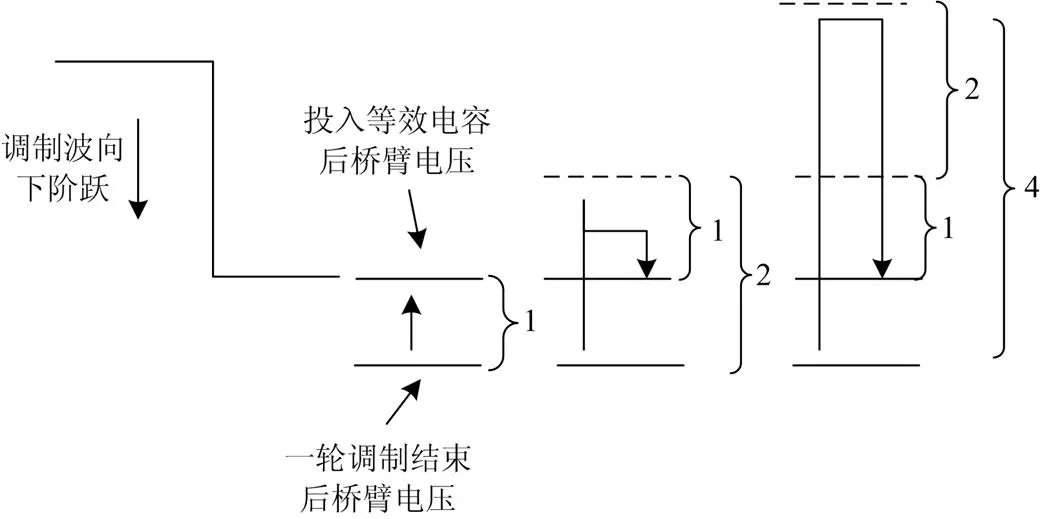
图5 等效电容组成过程

假如调制要求电压比桥臂电压高两个电平，可以选择正向投入一个逆变单元2的电容。如果2中的电容已经全部正向投入，可以选择正向投入一个3的子模块，同时反向投入一个1的子模块，相当于3-1。还可以选择正向投入两个1中的子模块，相当于1+1。当调制要求电压大于桥臂电压三个或四个电平，或者当桥臂电压大于调制要求时，可以用同样的方式组成等效电容。

另外，电容的正向投入包括从切除状态到正向投入状态和从反方向投入状态到切除状态。电容反向投入包括从正向投入状态到切除状态和从切除状态到反向投入状态，所以MGC-MMC有很好的灵活性和容错性。MGC-MMC的调制方法具体过程如图6所示。

在投切过程中需遵守以下规则：

规则1：为了保持电容电压的相对稳定，需要电容正向投入时，当电流为正向，电容电压小的优先投入充电，当电流为反向时，电容电压较大的优先投入放电。需要电容反向投入时，当电流为正向，电容电压大的优先反向投入放电，当电流反向时，电容电压小的优先反向投入充电。

规则2：因为电容数量相对普通MMC数量较少，为了保持电压相对稳定，增加投切次数，所以可以用较多的电容参与组成等效电容。

3 仿真验证

为了验证本文提出的MGC-MMC的效果和稳压策略，利用Matlab/Simulink搭建了1个1 MW/10 kV的电力系统仿真模型，仿真模型示意图如图7所示。两侧系统均采用双闭环标幺值控制[21-22]。其中一侧采用定有功功率控制和定无功功率控制，另一侧采用定直流电压控制和定无功功率控制。

图6 MGC-MMC调制方法示意图

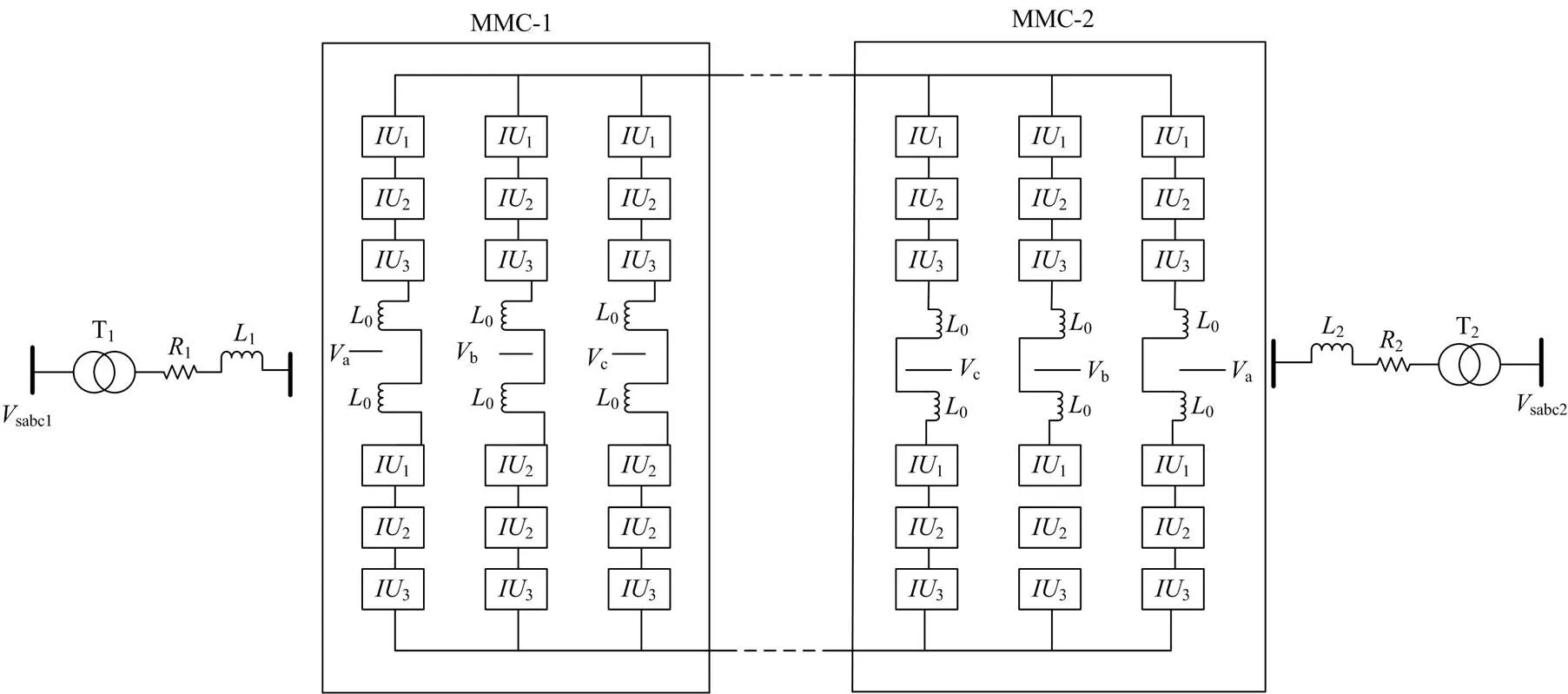
图7 电力系统仿真示意图

逆变单元1、2和3中子模块的数量分别为4个、3个和10个。根据式(1)，交流侧一共可以产生51个电平。经过计算，三组逆变单元子模块的电容电压值分别为205 V、410 V和820 V，其他重要参数如表1所示。

表1 部分仿真参数

3.1 子模块电容值计算

电容是子模块中最大的元器件，电容值将直接影响直流侧的运行特性[23]。本文将从抑制子模块电容电压波动和有功功率发生变化时系统的动态反应速度两个方向，对电容值进行计算。

在MMC的一个周期中，子模块电容的充放电可以表示为[24]

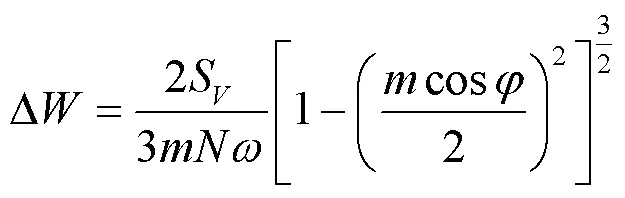
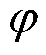
电容的储能表示为

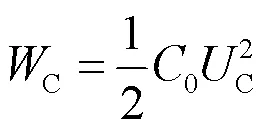
式中：C表示电容的实际电压值；C表示电容运行中的实际储能。

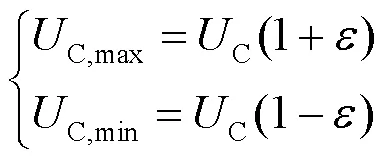
所以根据式(8)，电容的最大储能和最小储能分别为

根据式(9)可得，电容电压储能变化的最大值为

根据上述式(10)，为了抑制电容电压波动而选取的最小电容值计算公式为

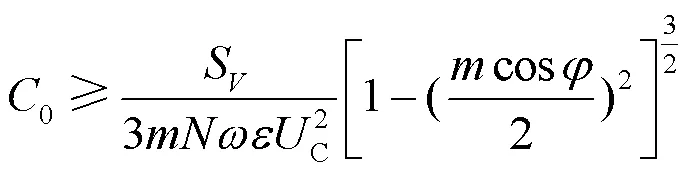
为了减少对有功功率的反应时间，所选取的最大电容值为[25]

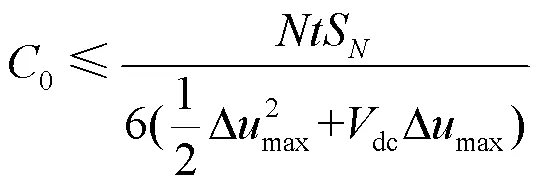
式中，是调整时间，本文设置为5 ms。电容电压波动值为10%。经过计算，1的电容最大值为9.5 mF，最小值为4.8 mF。考虑到设备成本等因素，本文选择三组逆变单元的电容值分别为6 mF、3 mF和1.5 mF。

3.2 直流侧仿真结果

经过电力系统仿真，直流侧电压值能够稳定在10 kV并且电压纹波小于5%，直流电流能够稳定在100 A，传输功率为1 MW。直流侧电压电流和有功功率的仿真结果如图8—图10所示。

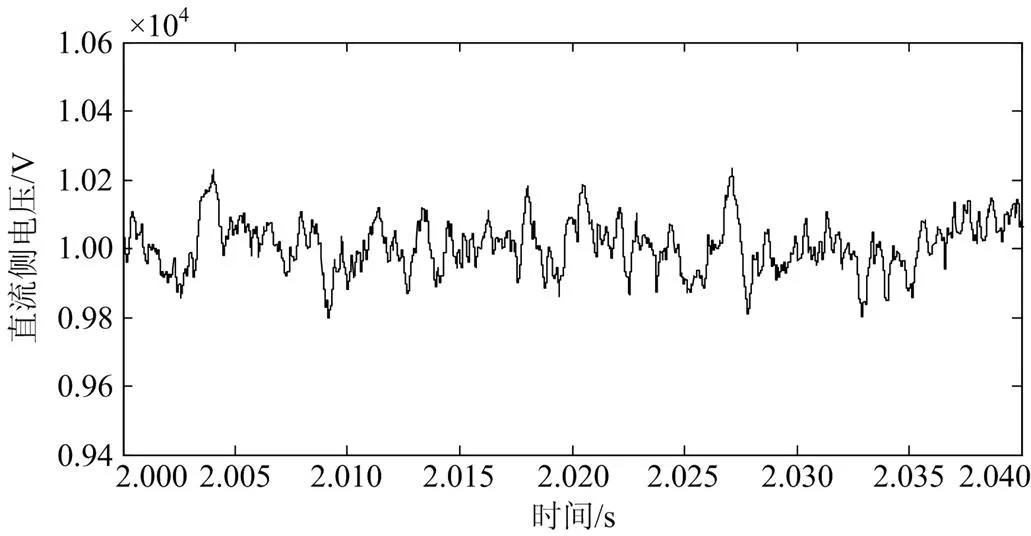
图8 直流侧电压仿真结果

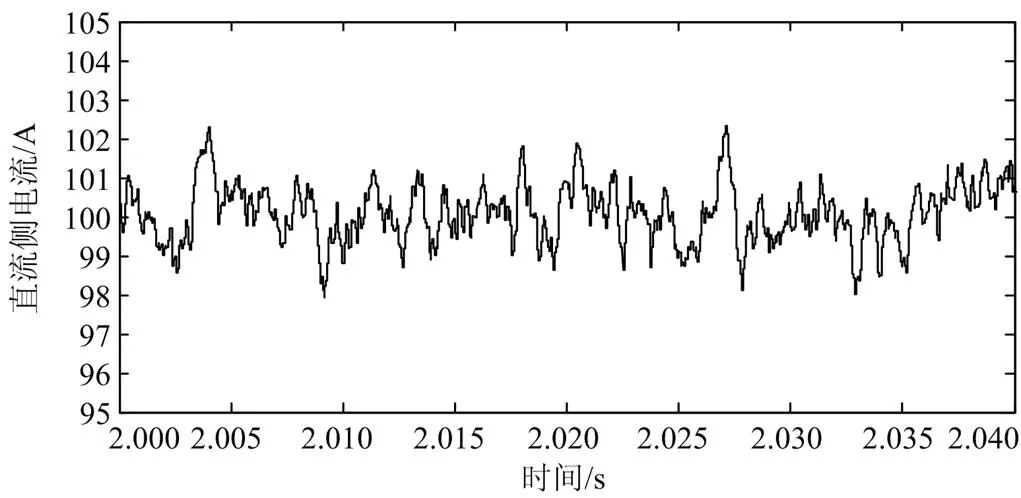
图9 直流侧电流仿真结果

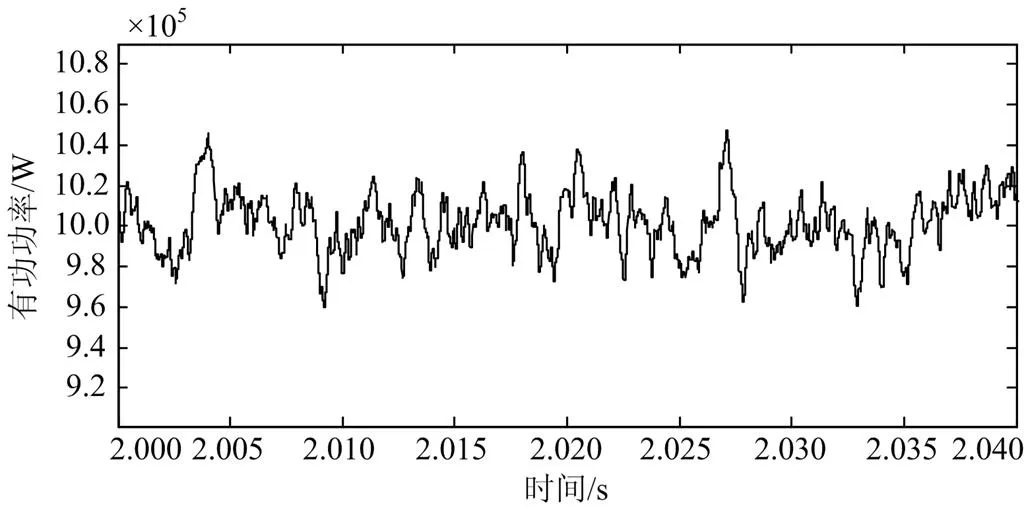
图10 有功功率仿真结果

3.3交流侧仿真结果

为了更直观地反应MGC-MMC的优点，以单相逆变器为例，搭建了子模块数量均为17的普通MMC和本文提出的MGC-MMC仿真模型，逆变侧仿真结果如图11和图12所示。在17个子模块的情况下。普通MMC只能输出18阶电平，而MGC-MMC在逆变单元子模块数量分别为4个、3个和10个的情况下可以输出51阶，通过调节子模块数量还可以输出更多电平。

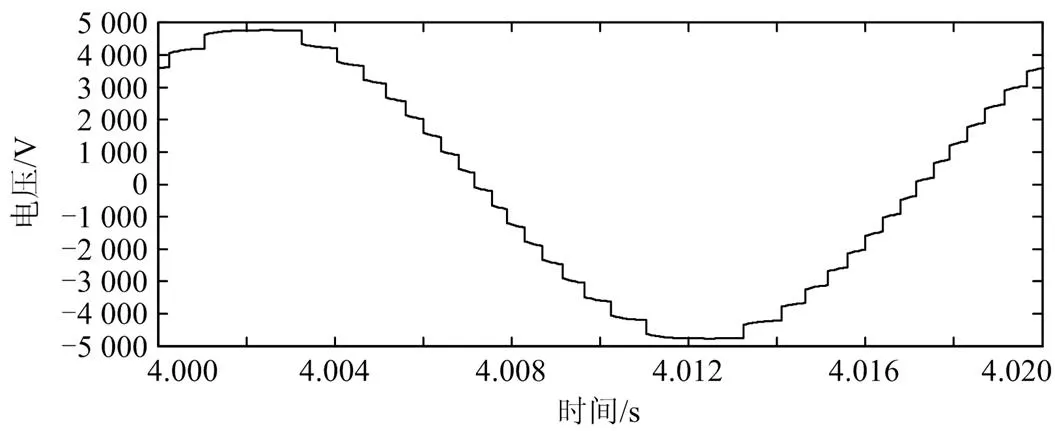
图11普通MMC单相交流侧电压仿真结果

图12 MGC-MMC单相交流侧电压仿真结果

经过两端电力系统仿真，逆变侧输出电压电流如图13和图14所示。因为两侧采用双闭环标幺值控制，所以输出值介于1和-1之间，波形接近于正弦波，证明MGC-MMC正常工作。进一步分析输出电压的波形质量，对交流侧输出波形进行快速傅里叶变换(THD)，结果如图15所示，谐波含量为0.61%。

整流侧输出波形和逆变侧相似。仿真结果显示在相同子模块数量的前提下，MGC-MMC能够输出比普通MMC更多的电平数量，并且输出的波形质量好，不需要其他的滤波器。

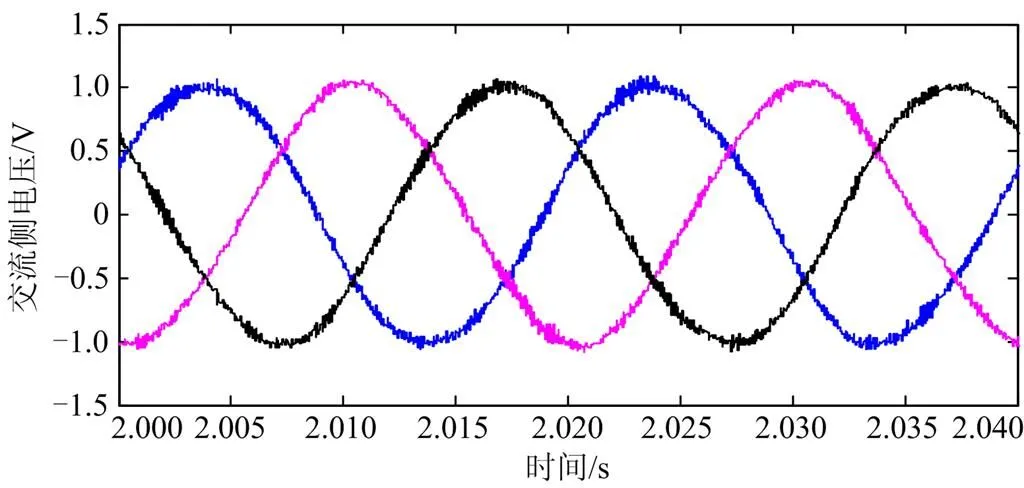
图13 交流侧电压仿真结果

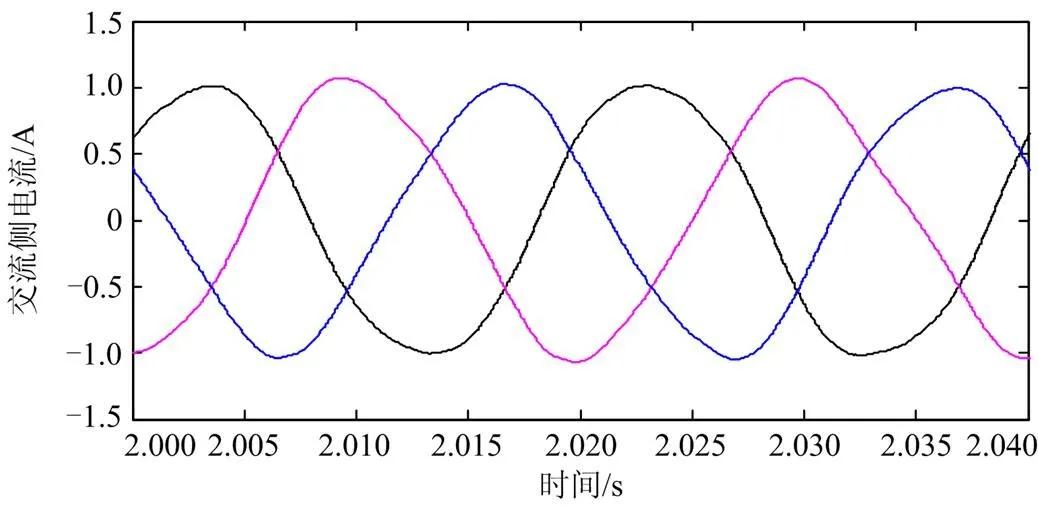
图14 交流侧电流仿真结果

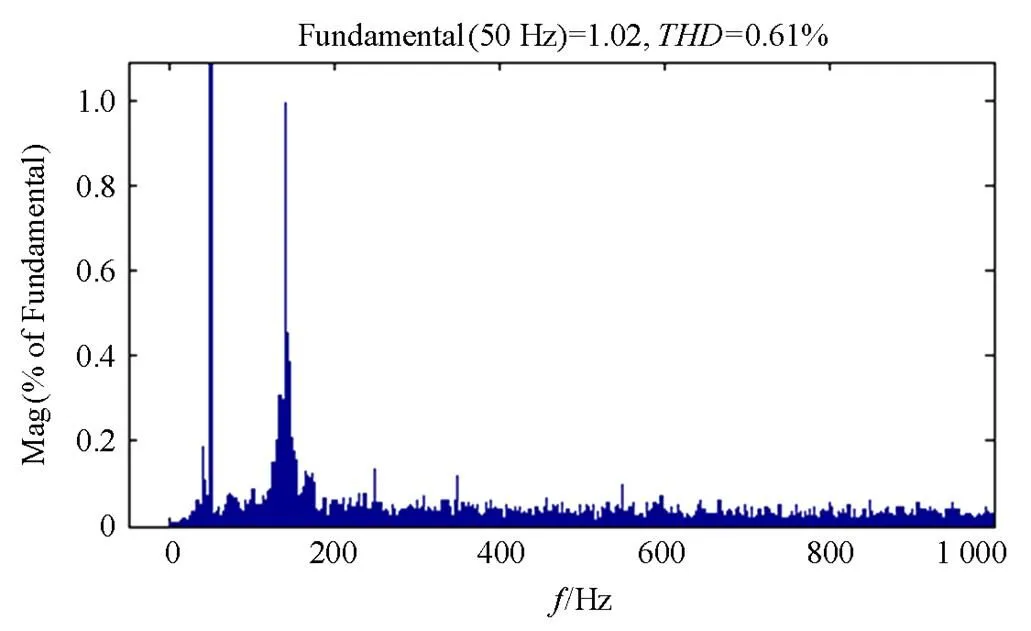
图15 输出电压FFT分析结果

3.4 逆变单元仿真结果

图16—图18为三组逆变单元的仿真输出结果，电容电压波动率满足小于10%的要求，与计算结果一致。

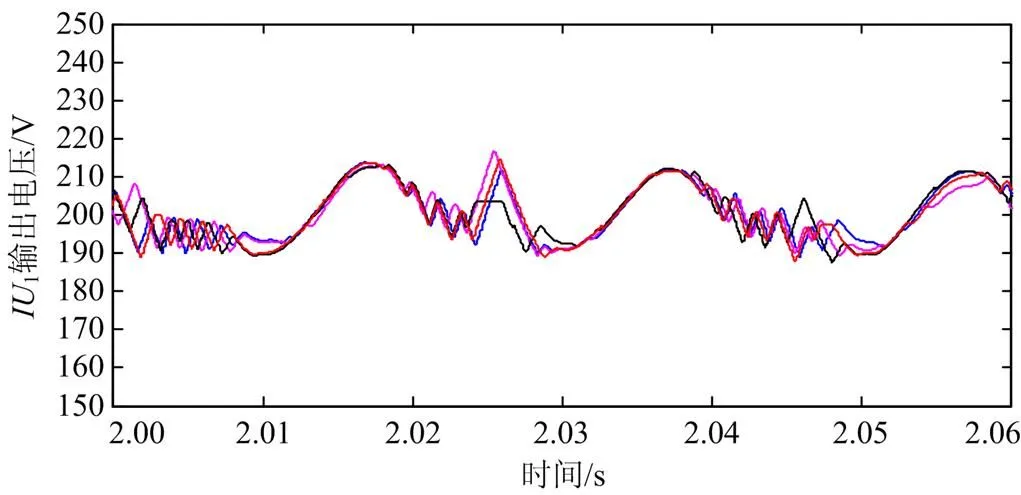
图16 逆变单元IU1输出电压

图17 逆变单元IU2输出电压

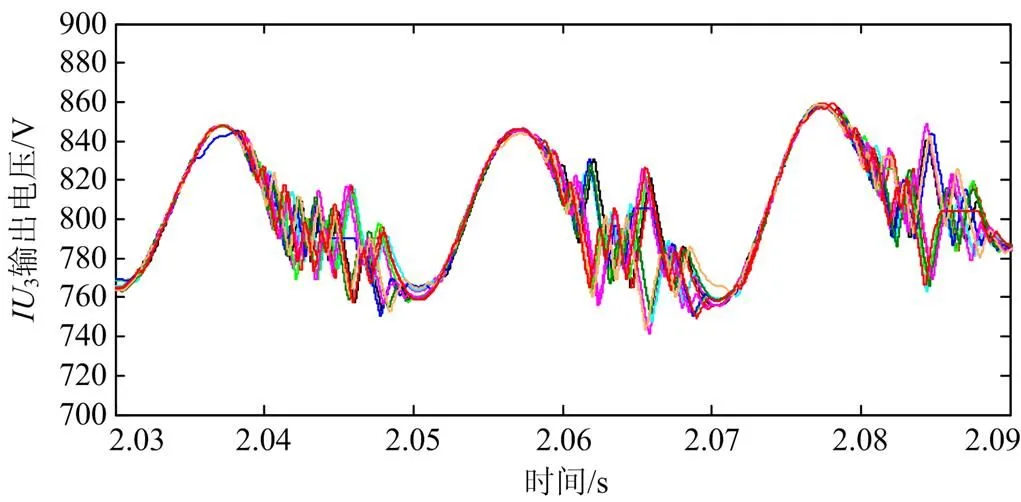
图18 逆变单元IU3输出电压

4 经济性验证

本文提出MGC-MMC的目的是降低MMC换流站的建设成本，因为换流站的建设成本主要在于子模块，所以本文从子模块的建设成本角度进行成本计算。考虑到MMC的冗余特性，三个逆变单元中的子模块各增加一个，普通MMC子模块的数量增加两个。电容的价格来自爱普科斯公司中国大陆经销商，IGBT价格来自英飞凌公司官网。具体价格和元器件参数如表2、表3所示。

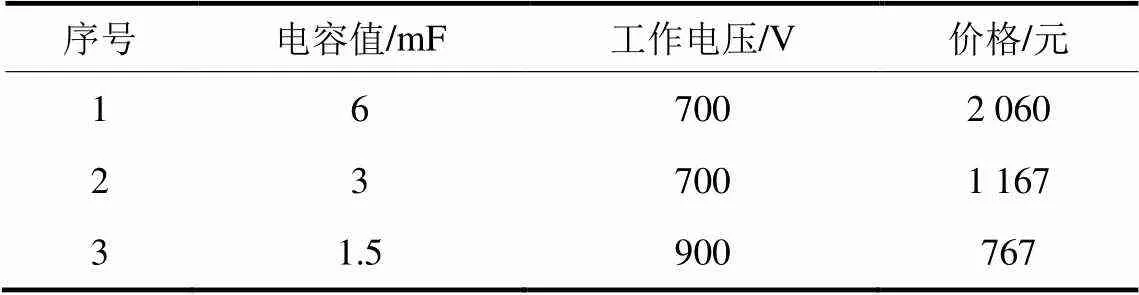
表2 电容参数

表3 IGBT参数

50电平MGC-MMC总价格如表4所示，50电平普通MMC总价格如表5所示。

经过计算，MGC-MMC的总价格仅为普通MMC的24.9%，MGC-MMC的总价格通过减少1、2的子模块数量，同时增加3的子模块数量还可以进一步减少。

表4 MGC-MMC总价格

表5 MMC总价格

5 结论

经过电力系统仿真，本文所提出的MGC-MMC电路拓扑和稳压策略能够稳定运行，与普通MMC相比，在子模块数量相同的情况下能够输出更多数量的电平，输出的波形质量能够满足柔性直流输电的要求。

现有的GC-MMC因稳压算法的限制，只能用于4个子模块的情况，由于子模块耐压值的存在，现有的GC-MMC无法应用于高压，而MGC-MMC不存在这个问题，可以通过增加逆变单元中子模块的数量来提高可以应用的电压等级。

通过成本计算，本文提出的MGC-MMC能够大大减少换流站建设成本。另外，对于MGC-MMC还有以下几点需要说明。

1) 本文提出的MGC-MMC中三组的电容值之比为4:2:1，也可以设置为3:2:1，还可以设置两组电容值之比为2:1的逆变单元，灵活性好。

2) 本文提出的稳压策略在交流侧输出170电平时仍然能够正常运行。

3) 因为需要对每个逆变单元中子模块进行排序，所以每个逆变单元中子模块数量最少为2个。

4) 本文所提出的MGC-MMC目前只有NLM调制法，PWM调制方法还需要做进一步的研究。

[1] 荣飞, 徐彦, 周保荣, 等. 柔性直流输电电压序列选择的研究[J]. 高压电器, 2020, 56(12): 203-211.

RONG Fei, XU Yan, ZHOU Baorong, et al. Research on voltage sequence selection of flexible DC transmission[J]. High Voltage Apparatus, 2020, 56(12): 203-211.

[2] 辛恩承. 高压直流输电线下空间电荷与电场的关系研究[J]. 电测与仪表, 2019, 56(5): 38-42.

XIN Encheng. Research on the relationship between space charge and electric fieldunder high voltage direct current transmission line[J]. Electrical Measurement & Instrumentation, 2019, 56(5): 38-42.

[3] 时伯年, 孙刚, 瞿艳霞. 柔性直流输电的孤网频率稳定协调控制[J]. 电力科学与技术学报, 2019, 34(04): 137-142.

SHI Bonian, SUN Gang, QU Yanxia. Research on coordinated frequency stability control after islanding based on VSC-HVDC technique[J]. Journal of Electric Power Science and Technology, 2019, 34(04): 137-142.

[4] XIE Xianda, et al. Fully adaptive ISO geometric topology optimization using MMC based on truncated hierarchical B-splines[J]. Structural and Multidisciplinary Optimization, 2021: 1-19.

[5] DAVID D. Interactions between a half-bridge MMC and a hybrid DC breaker during fault current interruption compared to a full-bridge MMC[J]. IET Power Electronics, 2021, 13(18): 4168-4175.

[6] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.

LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.

[7] 林强, 厉伟, 徐建源, 等. MMC子模块电压均衡及环流抑制方法研究[J]. 电工电气, 2021(1): 5-10.

LIN Qiang, LI Wei, XU Jianyuan, et al. Research on sub-module voltage balance and circulating current suppressing method of MMC[J].Electrotechnics Electric, 2021(1): 5-10.

[8] 王炳辉, 黄天啸, 吴涛, 等. MMC柔直换流站稳态无功能力研究[J]. 现代电力, 2021, 38(2): 164-170.

WANG Binghui, HUANG Tianxiao, WU Tao, et al. Research on steady-state reactive power capacity of flexible MMC-HVDC converter station[J]. Modern Electric Power, 2021, 38(2): 164-170.

[9] 田培涛, 吴庆范, 黄金海, 等. 基于LCC和FHMMC的混合多端直流系统线路保护方案研究[J]. 电力系统保护与控制, 2021, 49(1): 170-177.

TIAN Peitao, WU Qingfan, HUANG Jinhai, et al. Research on protection strategy of a hybrid multi-terminal DC system based on LCC and FHMMC[J]. Power System Protection and Control, 2021, 49(1): 170-177.

[10] 戴志辉, 黄敏, 苏怀波. 基于MMC的环状直流配网在不同接地方式下的故障特性分析[J]. 电力系统保护与控制, 2019, 47(1): 1-10.

DAI Zhihui, HUANG Min, SU Huaibo. Analysis on fault characteristics of MMC-based ring DC distribution networks under different grounding modes[J]. Power System Protection and Control, 2019, 47(1): 1-10.

[11] SONG Guobing, HOU Junjie, GUO Bing, et al. Pilot protection of hybrid MMC DC grid based on active detection[J]. Protection and Control of Modern Power Systems, 2020, 5(1): 82-96.

[12]王坤, 刘开培, 胡志鹏, 等. 适用于含大量子模块的MMC快速电容电压均衡策略[J]. 电网技术, 2017, 41(12): 3854-3861.

WANG Kun, LIU Kaipei, HU Zhipeng, et al. A fast capacitor voltage balancing strategy for MMC with large number of sub-modules[J]. Power System Technology, 2017, 41(12): 3854-3861.

[13]宋平岗, 罗剑, 游小辉, 等. 基于MMC的多端柔性直流输电系统控制策略研究[J]. 现代电力, 2017, 34(1): 55-61.

SONG Pinggang, LUO Jian, YOU Xiaohui, et al. Research on control strategy of multi-terminal HVDC based on MMC[J]. Modern Electric Power, 2017, 34(1): 55-61.

[14] 杜晓舟, 梅军, 邓凯, 等. 模块化多电平换流器电容电压均衡控制方法[J]. 电网技术, 2016, 40(1): 26-31.

DU Xiaozhou, MEI Jun, DENG Kai, et al. Voltage balance control method of MMC[J]. Power System Technology, 2016, 40(1): 26-31.

[15]邢长达, 郭家虎, 朱成杰, 等. MMC 控制系统中子模块控制器的设计[J]. 电力系统保护与控制, 2016, 44(3): 114-121.

XING Changda, GUO Jiahu, ZHU Chengjie, et al. Design of the sub-module controller of the MMC control system[J]. Power System Protection and Control, 2016, 44(3): 114-121.

[16] 于飞, 朱瑞峰, 刘喜梅. 阶调式模块化多电平变换器的研究及应用[J]. 电力系统保护与控制, 2019, 47(22): 27-34.

YU Fei, ZHU Ruifeng, LIU Ximei. Research on gradationally controlled modular multilevel converter and its application[J]. Power System Protection and Control, 2019, 47(22): 27-34.

[17]YAMADA M, IWATA A, OKADA J. A new voltage sag compensator with a gradationally controlled voltage inverter[C] // 2005 European Conference on Power Electronics and Applications, 2005, Dresden, Germany.

[18]LU X, SUN K, MA Y, et al. High performance hybrid cascaded inverter for renewable energy system[C] // 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), March 6-11, 2011, Fort Worth, TX, USA.

[19]DORN J, HUANG H, RETZMANN D. CIGRE novel voltage source converters for HVDC and FACTS applications[C] // CIGRE International Symposium Conference, 2007, Osaka: Japan: 1-8.

[20]管敏渊, 徐政, 屠卿瑞, 等. 模块化多电平换流器型直流输电的调制策略[J]. 电力系统自动化, 2010, 34(2): 48-52.

GUAN Minyuan, XU Zheng, TU Qingrui, et al. Nearest level modulation for modular multilevel converters in HVDC transmission[J]. Automation of Electric Power Systems, 2010, 34(2): 48-52.

[21]赵成勇, 李金丰, 李广凯. 基于有功和无功独立调节的VSC-HVDC控制策略[J]. 电力系统自动化, 2005, 29(9): 20-24, 30.

ZHAO Chenyong, LI Jinfeng, LI Guangkai. VSC-HVDC control strategy based on independent regulation of active and reactive power[J]. Automation of Electric Power Systems, 2005, 29(9): 20-24, 30.

[22]陈谦, 唐国庆, 胡铭. 采用dq0坐标的VSC-HVDC稳态模型与控制器设计[J]. 电力系统自动化, 2004, 28(16): 61-66.

CHEN Qian, TANG Guoqing, HU Ming. Steady-state model and controller design of a VSC-HVDC converter based on dq0-axis[J]. Automation of Electric Power Systems, 2004, 28(16): 61-66.

[23]赵成勇. 柔性直流输电建模和仿真技术[M]. 北京: 中国电力出版社, 2014.

[24] 徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2014.

[25]王姗姗, 周孝信, 汤广福, 等. 模块化多电平HVDC输电系统子模块电容值的选取和计算[J]. 电网技术, 2011, 35(1): 26-32.

WANG Shanshan, ZHOU Xiaoxin, TANG Guangfu, et al. Selection and calculation for sub-module capacitance in modular multi-level converter HVDC power transmission system[J]. Power System Technology, 2011, 35(1): 26-32.

A gradationally controlled modular multilevel converter and its application

YU Fei, WANG Zihao, LIU Ximei

(College of Automation & Electric Engineering, Qingdao University of Science & Technology, Qingdao 266061, China)

With the increasing voltage level of power systems, the number of serial sub-modules in the bridge arm of a modular multilevel converter (MMC) increases, and the hardware costs increase. This restricts its development in the direct current transmission system. In order to solve these problems, a new type of converter is proposed by analyzing the working principle of a multi-level converter and the existing gradationally controlled modular multilevel converter (GC-MMC). In order to solve the problem of capacitor voltage balance of the new inverter, a new voltage regulation algorithm suitable for the new inverter is proposed. Finally, in the Matlab/Simulink environment, a flexible HVDC transmission system based on the new inverter's double-terminal SCM unit value control is built and verified. The simulation results show that the output level of the new converter is more than that of the common MMC, and the quality of the waveform of the output AC and DC side can meet the requirements of DC transmission. Through the cost calculation of the new inverter and the common MMC respectively, the results show that the construction cost of the new inverter is much less than the common MMC.

MMC; gradationally controlled multi-level inverter; GC-MMC; capacitor voltage balancing controlled algorithm

10.19783/j.cnki.pspc.201639

国家自然科学基金项目资助(61803219)；山东省自然科学基金项目资助(ZR2020MF081)

This work is supported by the National Natural Science Foundation of China (No. 61803219).

2020-12-30；

2021-03-29

于 飞(1961—)，男，博士，硕士生导师，研究方向为高压柔性直流输电；E-mail: yyffqd@163.com

王子豪(1996—)，男，硕士，通信作者，研究方向为高压柔性直流输电；E-mail: wzhwzhzb@163.com

刘喜梅(1961—)，女，博士，博士生导师，研究方向为电力电子、智能控制。

(编辑 许 威)