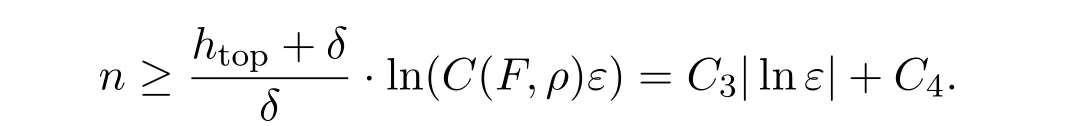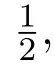具有F性质系统的拓扑熵和熵维数的关系

陈虎,历智明

(西北大学数学学院,陕西 西安 710127)

1 引言

文献[1]引入动力系统(X,f)拓扑熵的概念,它反映了系统的复杂性,拓扑熵是动力系统中经典的拓扑共轭不变量.文献[2]定义任意紧子集的拓扑熵.对于光滑系统(X,f),文献[3]证明了熵的有限性,即

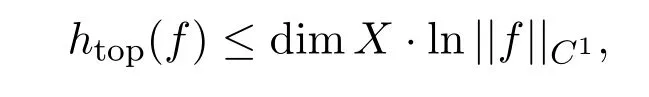
其中htop(f)是f的拓扑熵,dimX是流形X的维数,||f||C1是f的C1范数.更一般地对Lipschitz系统有

其中f是紧度量空间X到X的Lipschitz映射,dimBX是熵维数,L(f)是映射f的Lipschitz常数.

通常使用包含度量的熵另一种定义更加简洁;由于拓扑熵与度量无关,系统(1)可以进行如下改进:

其中D是诱导原空间拓扑的度量的集合,Lρ(f)是映射f相对于ρ的Lipschitz常数.

E.Ghys提出了以下猜想:如果X具有有限熵维数的紧度量空间,(X,f)是Lipschitz系统,则(2)式成立的充要条件是拓扑熵指数收敛.

文献[4]给出了E.Ghys猜想在自治系统下成立的充要条件:不等式(2)成立当且仅当拓扑熵htop(f)指数收敛.文献[5]给出了非自治拓扑动力系统下E.Ghys猜想成立充要条件.由于拓扑熵是刻画动力系统复杂程度的重要不变量,关于拓扑熵的研究国内外有许多重要的成果[6-14].

本文在上述研究的基础上,定义一类比Lipschitz系统与H¨older连续系统更为一般的系统,即(X,f)具有F性质,最后得到此类系统下Ghys猜想成立的充要条件是拓扑熵指数收敛.

2 预备知识

2.1 基本定义

定义 2.1设(X,ρ)是度量空间,给定映射f:X →X,称f是Lipschitz映射,如果满足

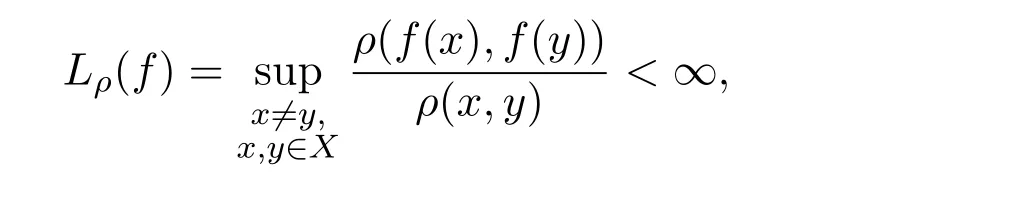
且称 Lρ(f)是 Lipschitz常数.

定义 2.2设(X,ρ)是度量空间,给定映射f:X →X,称映射f是H¨older连续,如果存在常数C＞0,α＞0,使得对任意x,y∈X,有

注记 2.1当α=1时,该映射为Lipschitz映射;当α=0时,该映射为有界映射.

定义 2.3设映射 F:R+→ R+,t→ F(t).设 (X,ρ)是度量空间,给定映射f:X→X,称f具有F性质,如果对任意x,y∈X满足

称(X,ρ,f)是具有F性质的系统.

注记 2.2(1)当F是线性映射时,即F(t)=kt(k＞0),该映射为Lipschitz映射;

(2)当F(t)=ktα(k＞0,α＞0)时,该映射为H¨older连续映射.因此具有F 性质系统比 Lipschitz系统和H¨older系统更为一般.

如果X是拓扑空间,f:X→X是连续映射,称(X,f)是拓扑动力系统.

定义2.4设(X,ρ)是紧度量空间,(X,f)是拓扑动力系统,对任意n∈N,ε＞0,称X 的子集 Y为(n,ε)张成集,如果对任意 x∈X,存在y∈Y,使得

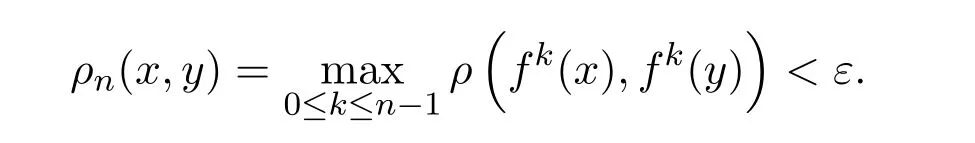
记 (X,f)关于度量 ρ最小的张成集的基数为 s(n,ε,ρ),在度量明确的情况下记为 s(n,ε).

定义 2.5设(X,ρ)是紧度量空间,(X,f)为拓扑动力系统,定义拓扑熵:

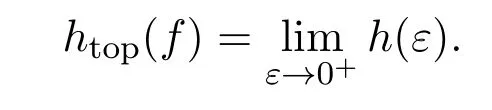
记S(r)是度量空间X中以r为半径的开球的r-网的最小基数.

定义 2.6设(X,ρ)是紧度量空间,(X,f)为拓扑动力系统,熵维数定义为

定义 2.7htop(f)是指数型收敛的,如果对任意δ＞0,存在常数Cδ,εδ＞0以及存在度量ρδ与原始度量 ρ拓扑等价,使得对任意0＜ε＜εδ,n＞Cδ·|lnε|,有下面等式成立

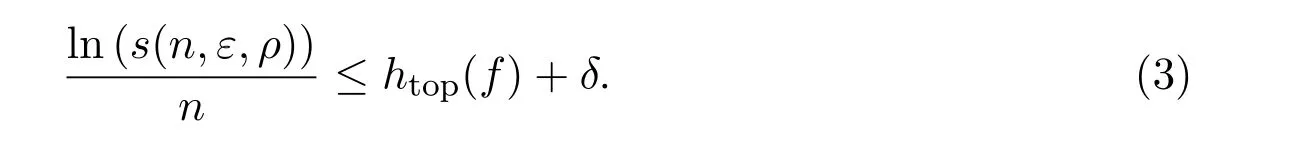
3 主要结论

下列定理给出了当(X,f)是具有F性质的系统时,拓扑熵、熵维数二者的关系式.在下文中,总是假设X是紧度量空间,(X,f)是具有F性质的系统.

定理3.1设(X,ρ,f)是紧度量空间上的拓扑动力系统,则有以下结论成立:

当f是Lipschitz映射时,

定义 3.1称(X,ρ,f)是具有F*性质的系统,如果F满足

(i)F单调递增;

(ii)F(0)=0;

(iii)存在 ε0＞ 0,C(F,ρ)＞ 0,使得对任意 ε∈ (0,ε0),n ∈ N,有

(iv)0 ＜ C(F,ρ)＜ 1.

定理 3.2设(X,f)是紧度量空间(X,ρ)上具有F*性质的拓扑动力系统,则有

定理 3.3设(X,f)是紧度量空间(X,ρ)上具有F*性质的拓扑动力系统,则拓扑熵指数收敛的充分必要条件是等式(4)成立

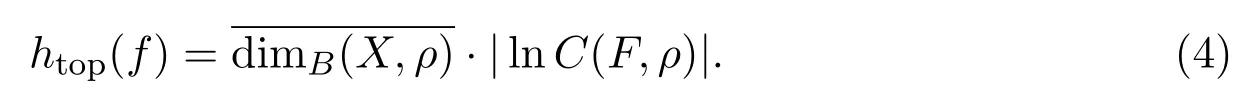
4 定理证明

4.1 定理 3.1的证明

定理3.1的详细证明可参见文献[15],为了文章的完整,本文将给出一个证明.

证明取L≤max(1,L(f)).由于f是Lipschitz映射,因此由Lipschitz映射的定义可以得到对任意x,y∈X,有ρ(f(x),f(y))≤Lρ(x,y).特别的,当0≤m≤n时有

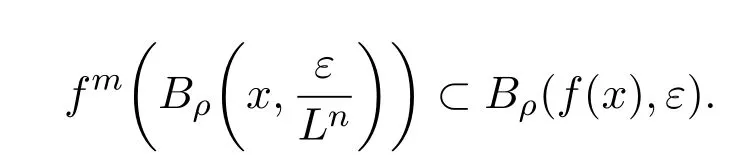
因此,对任意ε＞0,n∈N,x∈X 有

从而有

于是,可以得到下式成立

因此有

4.2 定理 3.2的证明

证明对任意x,y∈X,n∈N,有

由于(X,f)是具有F*性质的拓扑动力系统,所以存在ε0＞0,使得对∀ε∈(0,ε0),当 ρ(x,y)≤ C(F,ρ)nε,有 ρn(f(x),f(y))≤ ε.所以对任意 n ∈ N,ε∈ (0,ε0),可以得到

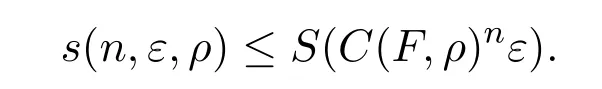
由 |ln(C(F,ρ)nε)|=n|lnC(F,ρ)|+|lnε|,可以得到下式成立

因此有

4.3 定理 3.3的充分性证明

显然,对任意α∈(0,1),上述级数是收敛的,从而mα(x,y)是X 上的度量.

引理 4.1对任意α∈(0,1),度量mα是在拓扑意义下等价于原始度量ρ.

证明由不等式mα≥ρ,diamX＜∞,以及f是连续的即可证明.

引理 4.2设 (X,ρ,f)是具有F*性质的系统,对任意 α∈(0,1),则在 mα下,有下列不等式成立

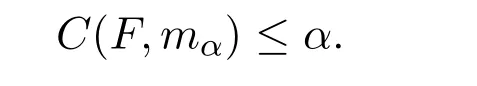
证明任意 ε0＞0,任意 ε∈(0,ε0),n＞N,x,y∈X,有 F-n(ε)≤ αnε.因此有

记Sα(r)是在度量mα下最小r-网的基数.

引理 4.3任意 ε0＞0,任意 ε∈(0,ε0),n＞0,考虑在度量 ρ下关于 f的 (n,ε)-网 NT(n,ρ,ε).那么在度量 mα下,以 NT(n,ρ,ε)中的点为球心,rδ为半径开球族可以覆盖X,其中

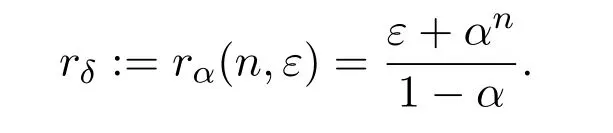
证明考虑任意一点 x∈X,假设 y∈NT(n,ρ,ε)是在度量 ρ下距离 x最近的一个点.计算x,y在度量mα下的距离

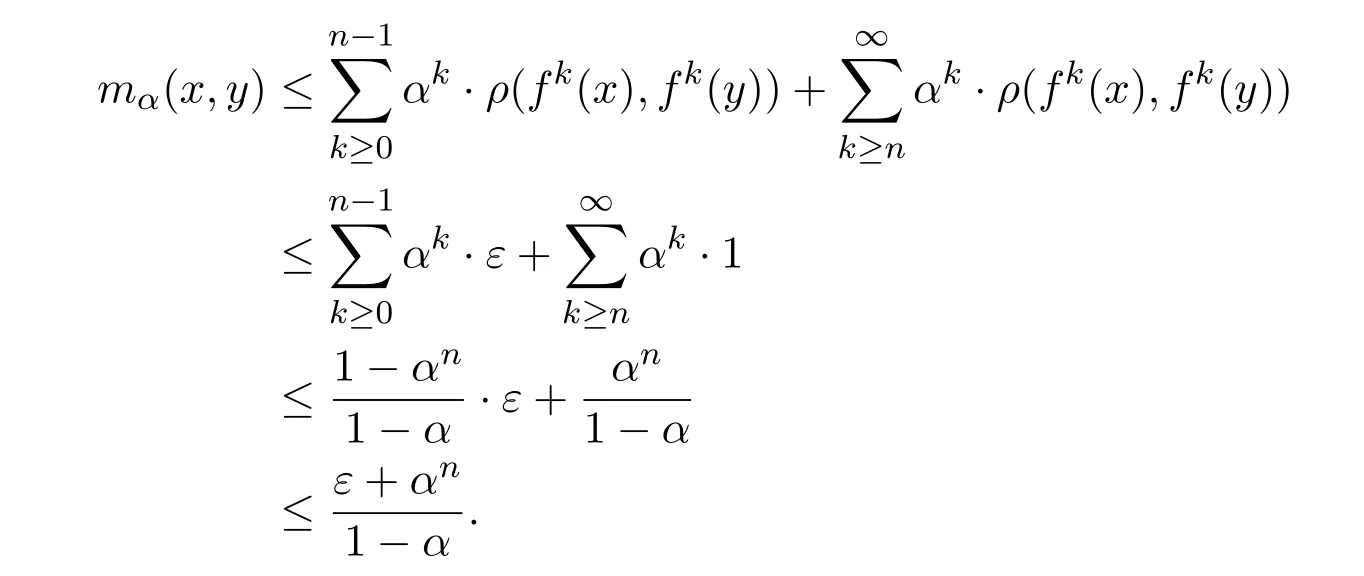
推论 4.1对任意r＞0和α∈(0,1),令

其中[x]是数字x的整数部分.那么

证明由引理4.3可得

将 ε = εα(r),n=n(r) 代入 (6) 式可得 S(rα(n(r),εα(r))) ≤ s(n(r),εα(r)).又因为有 rα(n(r),εα(r))≤ r,故可以得到 Sα(r)≤ s(n(r),εα(r)).

引理 4.4假设拓扑熵 htop(f)是指数收敛的,由定义 2.7,对任意 δ＞0,存在α,r0＞0,使得对任意r＜r0下列两个不等式成立.

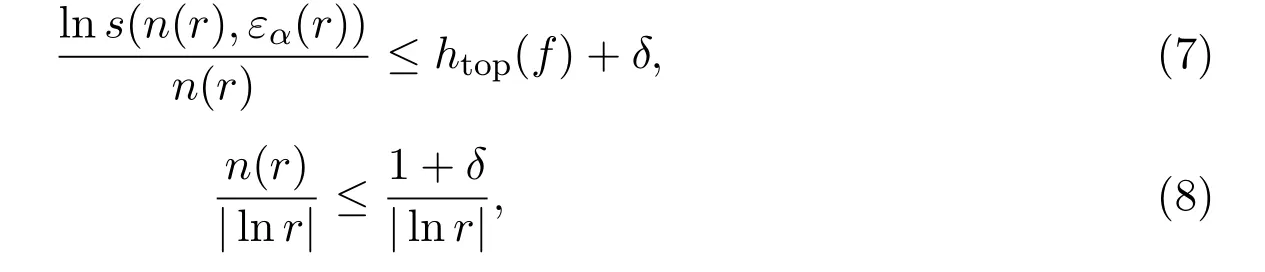
其中n和εα满足等式(5).

证明首先证明不等式(7),不等式(7)是由不等式(3)通过n=n(r)和ε=εα(r)得出.通过定义2.7,下列不等式成立

引入下列等式

取满足不等式(7)的α,于是有

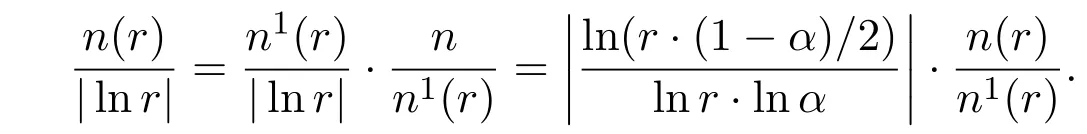
将上述结果代入不等式(8)中,可以得到

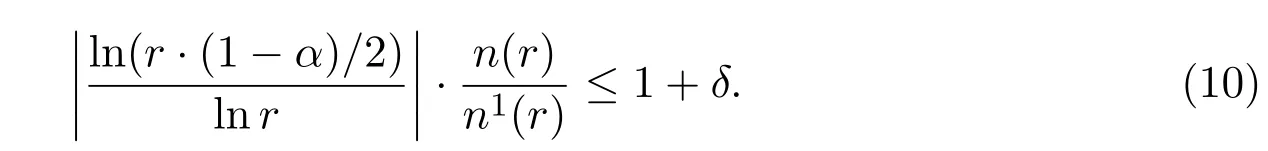
显然,当r→0,不等式(10)趋于1,因此存在r0＜0使得不等式(8)成立.

定理 3.3充分性的证明给定δ＞0,可以得到度量ρδ,通过定义2.7可知,存在常数Cδ＞0,由引理4.1和引理4.2,不难得到存在α使得对任意r＜r0有不等式(7)-(8)成立,由推论4.1和引理4.4,可以得到

记δ1=δ·(1+htop+δ),因此当δ→0时有δ1→0,通过引理 4.2,给上述不等式左边乘|lnC(F,mα)|,右边乘lnα,可以得到下列不等式

上述不等式对所有的r＜r0成立,极限当r→0+时,有下列不等式

对任意 δ1＞0,不等式(11)成立.不妨取δ1→0+,可以得到

因此,由定理3.2以及拓扑熵指数收敛的定义,充分性证毕.

4.4 定理 3.3的必要性证明

假设等式(4)成立,那么对于任意δ＞0,存在度量ρδ∈D,使得

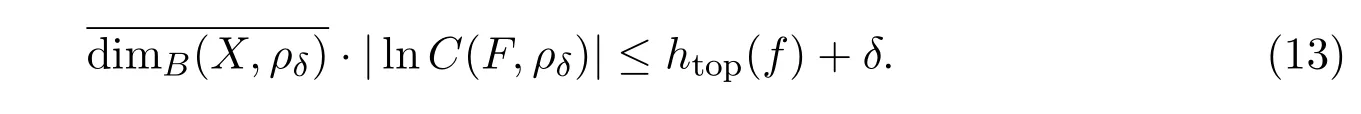
不失一般性,不妨假设 δ＜1,取满足不等式 (13)的任意 δ∈(0,1)和度量 ρδ.参照 Kushnirenko关于有限性的定理的证明,不妨取 C(F,ρδ)ε≤rδ,可以得到

由熵维数的定义有

对于不等式(13),由熵维数的定义可知,对任意初始点r≤r0,成立下列不等式

对任意 n≥0使得 C(F,ρδ)nε≤r0,由不等式 (14)有

可以得到

由第一个条件可以得到存在C1＞0,C2＞0,使得

由第二个等式,可以得到存在C3＞0,C4＞0,使得