一类非线性抛物型方程的最优系统和对称破缺

付丽敏, 王丽真,闫璐

(1.宁波大学数学与统计学院,浙江 宁波 315211;2.西北大学数学学院,陕西 西安 710127;3.西京学院理学院,陕西 西安 710123)

1 引言

本文讨论如下的非线性抛物型方程

的对称群,最优系统及其对称破缺.即基于最优系统的子代数分类如下的方程

抛物型方程和椭圆型、双曲型方程类似,也具有丰富的对称群,如标准的热方程

作为一类最简单的二阶线性抛物方程,有丰富的对称结构,它具有一个六维的李对称群[1-2],其中热方程的基本解可由它的t-x伸缩群或局部群来构造.非线性抛物型方程不仅具有李对称群,而且具有丰富的条件对称[3]、非局部对称[2]、非古典势对称[4]、广义条件对称群[5-8]、逼近势对称[9]和逼近条件对称[10]等.这些对称群可用于构造方程的精确解,并与抛物型方程的不变子空间、变量分离解和解的几何性质密切相关[11-12].一个自然的问题是是否有二阶的抛物型方程具有七维以上的李点对称群.事实上,人们已经发现了两个具有七维李对称群的二阶非线性抛物型方程.一个是仿射不变的热方程[13-14]

另一个是方程(1).方程(4)是仿射几何中的热流方程,即等价于平面仿射几何中的热流[13-14]

其中γ(t,s)表示在时刻t曲线的位置向量,σ表示曲线γ的仿射弧长参数.

若γ=(x,u(t,x)),则u(t,x)满足方程 (4).而在平面欧氏空间中的热流γt=γss等价于如下的热方程[15-16]

该方程又称为曲线收缩方程,相对应的欧氏空间中的热流(5)又称为曲线收缩流,关于平面欧氏和仿射几何中的热流在过去几十年里有很多的研究,产生了很多有趣的结果[13-16].平面欧氏和仿射几何中的热流可以看成广义曲线收缩流[17]γt=|κ|σ-1κn的特殊情形,其中n和κ分别是γ的单位法线和欧氏曲率.而对应于局部图的方程为一般的非线性抛物方程

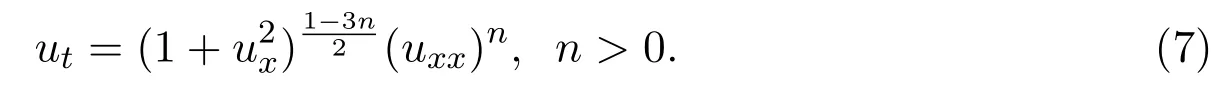
注意方程(4)和方程(6)分别是方程(7)的特殊情形.

众所周知,一个偏微分方程的李点对称群刻画了方程的不变性质和其所描述的重要的物理现象,而且对求解偏微分方程的精确解和对称约化有重要作用.由于偏微分方程的李对称群满足该方程的线性化方程,任何两个李对称的线性组合仍是一个李对称.因此确定哪些子群会给出本质上不同类型的解,对于完全理解方程的不变解是必要和重要的.李代数和李群中一个重要问题是给定一个有限维李群,如何分类不等价的子代数或子群.考虑到对应的方程的群不变解,即分类不等价的群不变解.这就导致了李代数的最优系统的概念[1,18].人们已经发展了多种构建最优系统的方法.文献[1]提出了构造热方程的李对称代数的最优系统,并给出了证明最优性的方法,其中李代数的Killing型,作为伴随作用的不变量,起到了核心的作用.一些系统的对称群的最优系统得到了系统的构造[19-21].文献[22]发展了Olver的方法得到了仿射热流的对称群的最优系统,并通过构造许多伴随作用的局部不变量给出了证明.文献[23-24]提出了把构造一般伴随作用的不变量归结为求解不变量所满足的一阶非线性偏微分方程组.其中,李代数的Killing型是该一阶偏微分方程组的特解.

给定一个具有丰富对称群的物理系统,一个自然的问题是在什么附加条件下,如外力场、磁场、电场和耗散等,该系统的对称性不再保持,关于该问题已经有许多研究.如文献[25]研究了薛定谔方程的对称破缺,文献[22,26]研究了一维和二维抛物型方程的对称破缺.本文将借助于方程(1)的最优系统研究它的对称破缺.

本文的结构如下:在第二节,构造方程(1)的对称代数的最优系统,通过寻找伴随作用的不变量,给出其证明,并给出了高维子代数的最优系统的构造;第三节利用最优系统得到了方程的对称约化;在最后一节,研究了方程(1)的对称破缺,即对于任意的子群,将给出函数F(x,t,u,ux)的最一般的形式,使得二阶非线性抛物方程

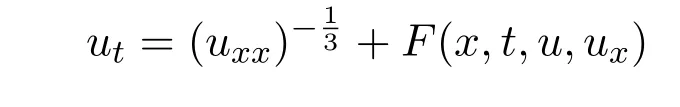
在任意的子群下保持不变.

2 最优系统

在这一节,构造方程 (1)的对称群的最优系统.利用李对称群方法[1,27],易得方程(1)的七维李对称群G由下列向量场生成[11]:

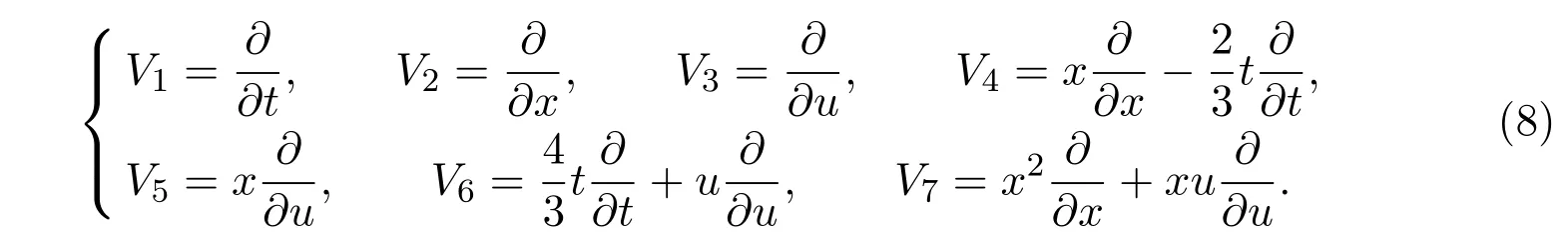
根据李的一般理论,李对称群(8)在通常的李括号下形成一个李代数G,运算关系如表1所示.为了构造李对称群 (8)的最优系统及证明其最优性,还需要计算李对称群(8)的对偶作用.

表1 李括号运算表,元素(i,j)表示李括号[Vi,Vj].

由表1和伴随表达式

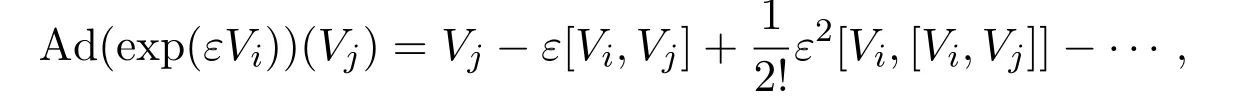
可以计算对称群G在G上的伴随作用,结果呈现在表2中.不变量对最优系统的构造和证明至关重要,因此,先回顾一下不变量的概念.G是由G生成的李群,定义在李代数G上的实函数φ,如果对于任意的V∈G,g∈G,都有φ(Ad(g)V)=φ(V),则称 φ为不变量.接下来运用文献[23]中的方法计算方程(1)的李对称代数G上的不变量φ.

表2 伴随作用表,元素(i,j)表示伴随作用Ad(exp(εVi))(Vj).

Ad(exp(εW))(V)

=(a1V1+ ···+a7V7)- ε[b1V1+ ···+b7V7,a1V1+ ···+a7V7]+O(ε2)

=(a1V1+ ···+a7V7)- ε(Θ1V1+ ···+ Θ7V7)+O(ε2),

其中

对于任意的 bi(i=1,···,7),都有

注意到如上方程对任意的bi成立,得到关于不变量φ(a1,a2,···,a7)的七个微分方程

解此偏微分方程组,可以得到两个基本不变量 A≡φ(a1,a2,···,a7)=a24-4a2a7,B≡φ(a1,a2,···,a7)=2a6-a4.利用所求的不变量可以构造最优系统,下面叙述本节的主要结果.

定理2.1李对称代数G的一维最优系统G1由下列一维子代数组成

其中

在前面已经证得A=a24-4a2a7是一个不变量.为了约化V,需要分别考虑以下三种情况.

(i)若a4-2a6=0,取

(ii)若 a4-2a60,a6=0,取

(iii) 若 a4-2a60,a60 且 a4-a6=0,取

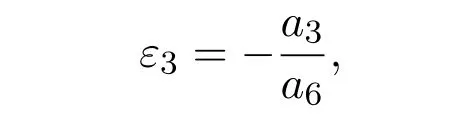
(iv) 若 a4-2a60,a60 且 a4-a60, 取 ε3=则=0,V 等价于 V4+αV6,α0,1.

情况2:A=0.在这种情况下,需要考虑两种情况:

情况2.1:a2,a4和a7中至少有一个不为零.如果a7=0,那么a4=0,a20.如果 a70,可以选择 ε2和 ε7使 1- ε2ε7=由方程组(12)可知,

为了进一步简化 V,把 Ad(exp(ε5V5))Ad(exp(ε3V3))和 Ad(exp(ε1V1))作用到上,得到一个新的,其中系数变为

根据a6=0的取值是否为零,可以分以下两种情况进行讨论.

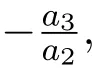
(ii)若 a60,将

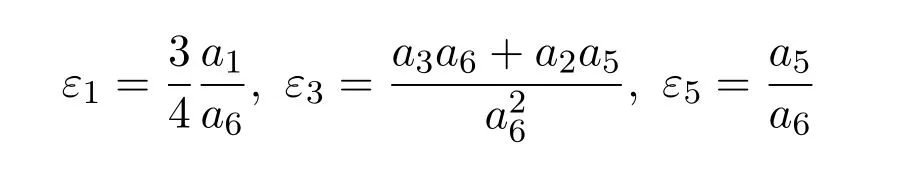
情况2.2:a2=a4=a7=0.此时,V等价于a1V1+a3V3+a5V5+a6V6.

(i)若 a60,用 Ad(exp(ε5V5))Ad(exp(ε3V3))和 Ad(exp(ε1V1))消去 V1,V3,和 V5,则V等价于V6.

(ii)若 a6=a5=0,用 Ad(exp(ε4V4))和 Ad(exp(ε6V6))约化 V1和 V3的系数,则V等价于V1,V3,V1+V3或V1-V3.

(iii)若 a6=0,a50,用 Ad(exp(ε2V2))消去 V3,用 Ad(exp(ε4V4)),Ad(exp(ε6V6))约化V1和V5的系数,则V等价于V5,V1+V5或V1-V5.

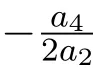
(i)若 a6=0,利用 V1,V3和 V5生成的群的伴随作用消去 V3和 V5,再用Ad(exp(ε6V6))约化V1的系数,使得V等价于V2+V7,V2+V7+V1或V2+V7-V1.

(ii)若 a60,利用 V1,V3和 V5生成的群的伴随作用消去 V1,V3和 V5,再用Ad(exp(ε4V4))约化 V6的系数,使得V 等价于V2+V7+V6或V2+V7-V6.

综上所述,已经证明了G中任意的一维子代数都等价于{r1,···,r20}中的一个.接下来需要去证明这些子代数之间的不等价性.要实现这一点,可以采用文献[21]中的方法,构造更多伴随作用的局部不变量.

引理2.1C是一个不变量,其中

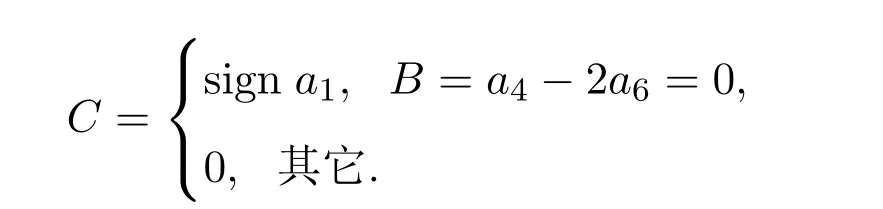
引理 2.2D,E,F,G都是不变量,其中

由表2易知,当a4=a7=0时,方程组(15)中sign a2不变,D是一个不变量.当a2=a5=a6=0时,方程组(16)中sign a3不变,E是一个不变量.当a4=a6时,在Ad(exp(ε5V5))的作用下,方程组(17)中5=a5+ε5(a4-a6)=a5,易见,F 是一个不变量.当a2=a4=0时,方程组(18)中sign a7不变,G也是一个不变量.最后,计算在每一个ri上所有不变量的取值,并把结果呈现在表3中,其中α0,,1.从这个表中能清晰的看到所有的ri之间是不等价的,因此它们构成一个一维的最优系统,定理2.1证明结束.

表3 不变量的值.

接下来,构建 G的一个二维最优系统,即确定李代数 G的所有二维子代数.令M=〈V,W〉表示由向量V和W 张成的子代数.事实上,只需要找到〈V,Wi〉形式的所有子代数,其中 Wi=ri,i=1,2,···,20,在定理 2.1中已经给出,V∈NorG(Wi).通过复杂的计算和化简,发现二维最优系统G2由以下子代数生成:

根据文献[18],可知任意一个三维子代数都包含一个二维子代数或者同构于O(3).因此可以通过扩充二维最优系统构建三维最优系统G3.省略繁琐的计算细节,最后发现三维最优系统G3由下面这些子代数生成:

3 对称约化

在本节中,利用定理2.1中的一维最优系统,将难以处理的非线性抛物型方程(1)约化为更简单的常微分方程,约化后的方程有更少的变量也更容易求解.下面介绍几种对称约化和不变解,其它情况与之类似.

将方程(19)代入方程(1)可知,υ(y)满足约化的常微分方程

令w=υy,方程(20)可进一步约化为一阶的常微分方程

其中t0是一个任意常数.

因此,群不变解为

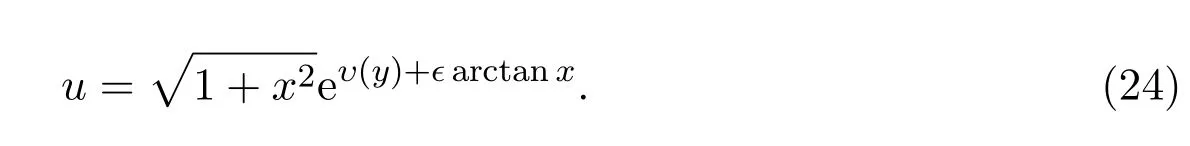
将方程(24)代入方程(1)可知,υ(y)满足约化的常微分方程

令w=vy,则w满足下面方程

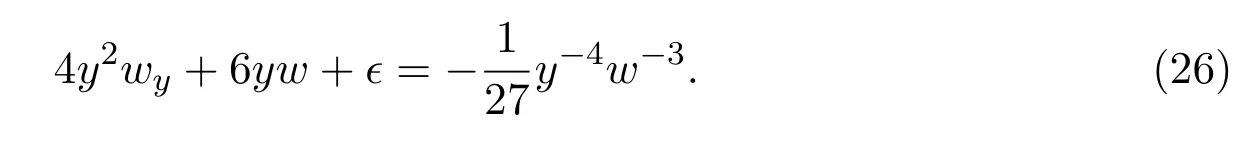
4 对称破缺

在本节,主要研究方程(1)的对称破缺.即对对称群G的每一个子群g,给出函数F(x,t,u,ux)的最一般的形式,使得方程(2)在这些子群下保持不变.现在考虑G的一个一维子群g,对应的无穷小生成元表示为V,

其中ξ,τ,η是关于x,t,u的可微函数.根据偏微分方程的不变性的无穷小准则[1,27],方程(2)在群g下是不变的当且仅当

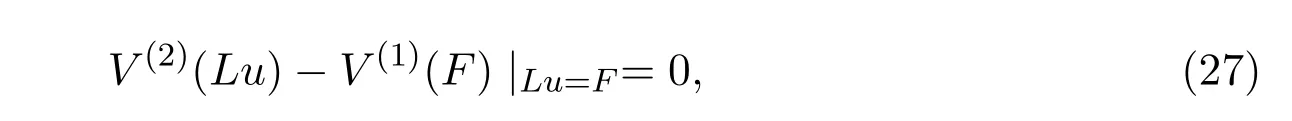
其中ηx是关于x,t,u,ux的光滑函数,b是关于x,t,u的任意函数.为了确定函数F,求解特征方程

一般来说,由方程组(29)的前三个方程得到向量场V的三个不变量,F是已知函数和这些不变量的任意函数的乘积.对于G的r-维子群(r＞1),方程(27)变成由r个方程组成的方程组,通过解这个方程组的特征方程可以求出对应的函数F.

在定理2.1中已经得到了所有的一维子代数.

下面考虑其中一个子代数r18=V2+V7+ϵV6,并介绍其详细的计算过程.

首先,求r18的二阶延拓,注意到方程不含uxt项,则

将这个结果代入到方程(28)中,可以得到如下的一个一阶偏微分方程

方程(30)的特征方程为

解此特征方程的前三个等式可以得到三个不变量

进一步,从方程组(31)的最后一个等式导出函数F的一般形式

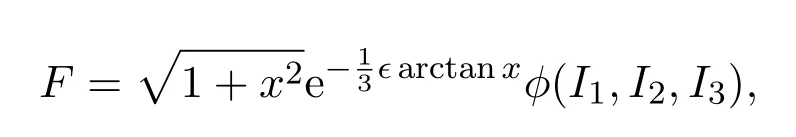
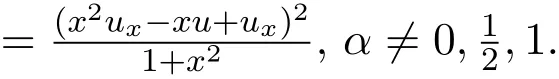
表4 一维最优系统下使得方程(2)保持不变的函数F.

结合一维子代数已得到的结果,可以求对应于二维子代数的函数F.下面以二维子代数s36=〈r4,r6〉为例介绍其详细的求解过程.余下的结果如表5所示.

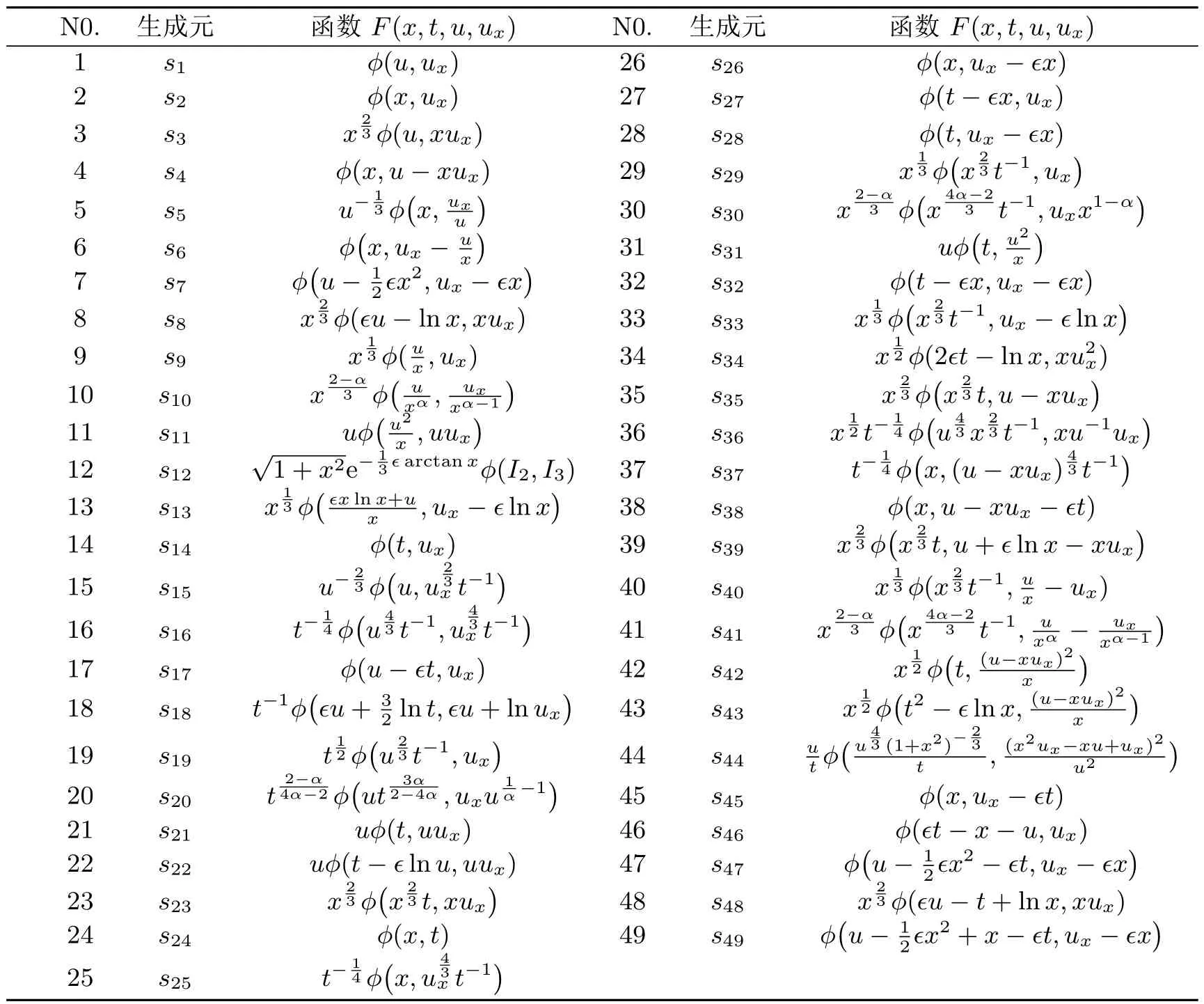
表5 二维最优系统下使得方程(2)保持不变的函数F.

在表4中,发现对应于一维子代数r4的不变函数为

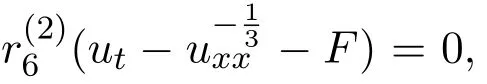
其中,φi,i=1,2,3表示φ(y1,y2,y3)对第i个变量求偏导.方程(34)对应的特征方程为

求解此特征方程的前两个等式可以得到两个不变量

再计算特征方程的第一项和最后一项的等式,得到在s36下使得方程(2)保持不变的函数为

将表 4和表 5中的结果结合起来,得到了表6中所列的三维子代数对应的函数 F.例如 m30=〈r3,r4,r6〉.方程 (2)在 r3下的不变性意味着函数 F不显含 u,即F=φ(x,t,ux).其次,由方程在r4下的不变性,可得

表6 三维最优系统下使得方程(2)保持不变的函数F.

最后,再由它的不变性,易得