广义单调性与广义凸性*
赵 宇,康兆敏,刘 琳,刘春妍,黄金莹
(佳木斯大学理学院,黑龙江 佳木斯 154007)
0 引 言
通过研究函数凸性的梯度刻画,获得梯度向量映射的单调性,反过来可作为函数凸性的有力判据.随着函数凸性的不断推广以及相应的梯度刻画结论的获得,单调映射的概念也不断地被推广并加以研究,这不仅使得广义凸性的刻画更加丰富,同时也极大丰富了优化理论内容 .1976 年,Karamardian[1]提出伪单调性;1990 年,Karamardian和 Schaible[2]提出拟单调性,并给出了伪凸性与伪单调性、拟凸性与拟单调性之间的等价性.以此为开端,国内外学者依托广义凸性的研究,相应演绎出大量的广义单调性概念.2003年,Yang等[3]建立预不变凸函数与一些广义单调性之间的关系;2004 年,Singh 和 Pini[4]建立了G-广义凸性与G-广义单调映射之间的关系;2007 年,彭再云等[5]建立了G-伪凸性与G-伪单调性;2014年,陈乔和罗杰[6]提出了E-伪单调性和E-拟单调性;2016年,杨新民和戎卫东[7]对广义单调性的基础性工作做了较为全面论述.近几年来,广义凸性又有了新的推广.2017年,黄金莹等[8]和赵宇等[9]通过在点集上建立广义凸结构的方法,给出并研究了F凸函数、F拟凸函数.
本文将在以上文献的基础上,结合文献[8-9]的广义凸结构理论,建立相应的F单调映射、F伪单调映射和F拟单调映射概念,进一步研究广义凸性与广义单调性之间的关系.
1 单调映射概念
定义1设非空集合K⊆Rn,向量值函数F:称F是K上的广义凸结构,如果F满足以下4个条件:
(4)F关于λ在[0,1]上连续(λ连续性).
定义2设F是K⊆Rn上的广义凸结构,且F关于λ在[0,1]上可微,∇:K→ Rn为映射.
(1)称∇是K上的F单调映射,如果对有
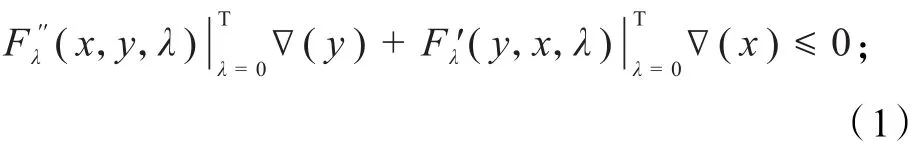
(2)称∇是K上的F伪单调映射,如果对x,y∈K且
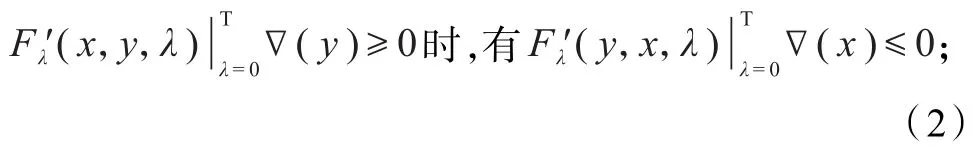
(3)称∇是K上的F拟单调映射,如果对x,y∈K且
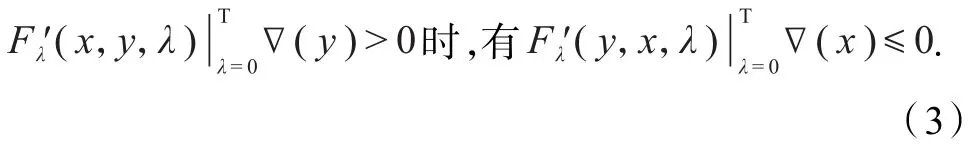
注1约定符号的 含 义 是表示转置.从定义2可以直接得到,F单调映射一定是F伪单调映射,F伪单调映射一定是F拟单调映射.
注 2在定义 2中,特取则
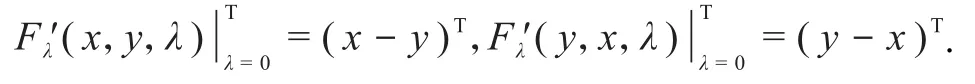
代入式(1)中得,
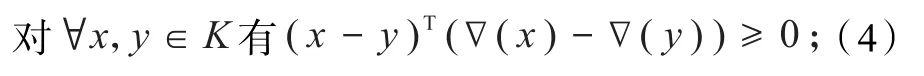
代入式(2)中得,
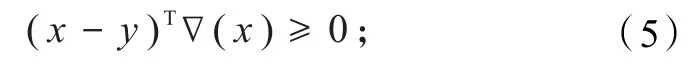
代入式(3)中得,
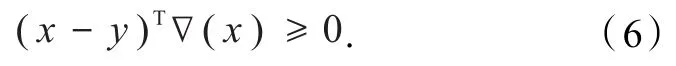
式(4~6)分别是单调映射、伪单调映射和拟单调映射的具体定义.
定义3设非空集合K⊆Rn,向量值函数F:K×K×[0,1]→ Rn是K上的广义凸结构,称K是关于F的凸集,如果

定义4设K⊆Rn是关于F的凸集,实值函数f:K→ R 满足:∀x,y∈K有F(x,y,0)=y,称f是K上的F伪凸函数,如果对∀x,y∈K且f(y)>f(x),∃α,τ> 0,当λ∈[0,τ]时,有
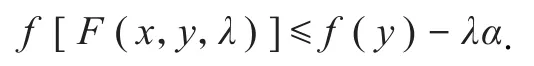
引理1设K⊆Rn是关于F的开凸集,实值函数f:K→ R 满 足 :∀x,y∈K有F(x,y,0)=y,f[F(x,y,1)]≤f(x)且F关于λ在 [0,1]上可微,f:K→ R 在K上 可 微 ,∇f:K→ Rn为f的 梯 度 向量,则:
(1)f是K上的F凸函数,当且仅当对∀x,y∈K有
(2)f是K上的F伪凸函数,当且仅当对x,y∈K且时,有
(3)f是K上的F拟凸函数,当且仅当对x,y∈K且
证明 仅证(2).首先证明必要性.
设x,y∈K且f(y)>f(x),由定义4知,∃α,τ>0,当λ∈ [0,τ]时,有f[F(x,y,λ)]≤f(y)-λα.
由F(x,y,0)=y, 可 将 上 式 变 形 为从而
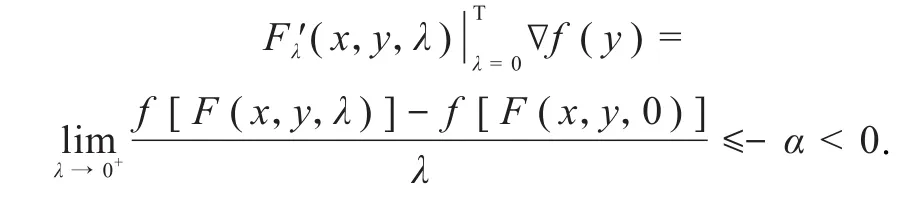
下面证明充分性.由充分性条件可知,当x,y∈K且
取定α(>0)使之满足:0,即有
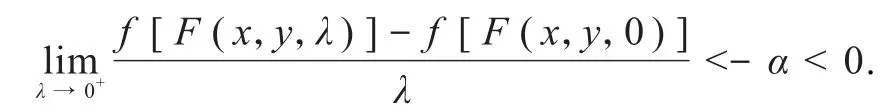
从而∃τ∈(0,1],使得当λ∈[0,τ]时,有即
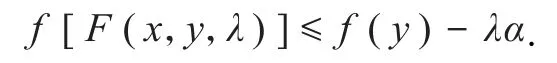
注3对于引理1结论(3),可将前提条件
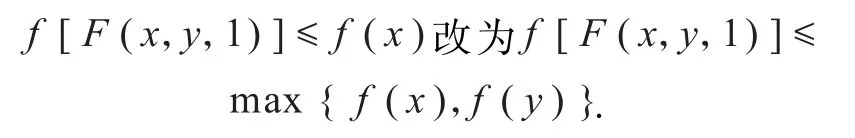
引理2设F是K上的广义凸结构,且其中x,y∈K,u1,u2∈[0,1],F关于λ在[0,1]上可微,则
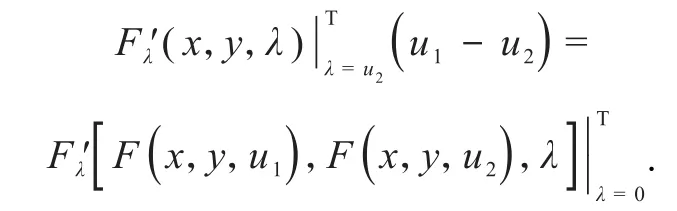
2 广义凸性与广义单调性之间的关系
定理1 设K⊆Rn是关于F的开凸集,实值函数f:K→ R 满 足 :∀x,y∈K有且F关于λ在[0,1]上可微,f:K→ R在K上可微,则f是K上的F凸函数,当且仅当∇f是K上的F单调映射.
证明 必要性.由引理1结论(1)知,当f是K上的F凸函数时,对∀x,y∈K有
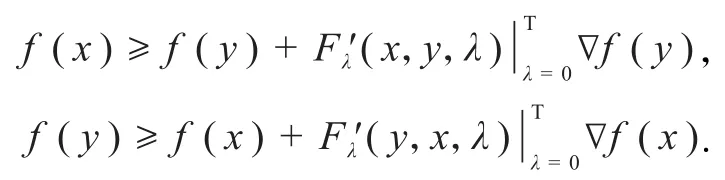
两式相加即得
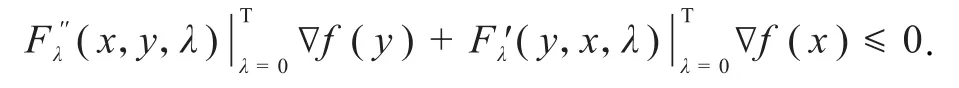
所以,∇f是K上的F单调映射.下面利用反证法证充分性.
设∇f是K上的F单调映射,但f不是K上的F凸函数 ,则
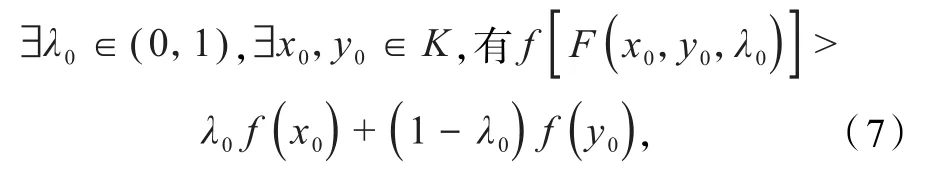
就有
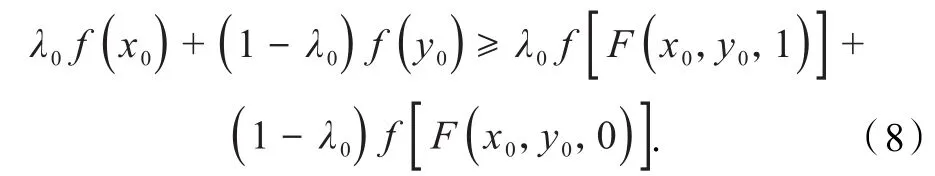
由式(7~8)得
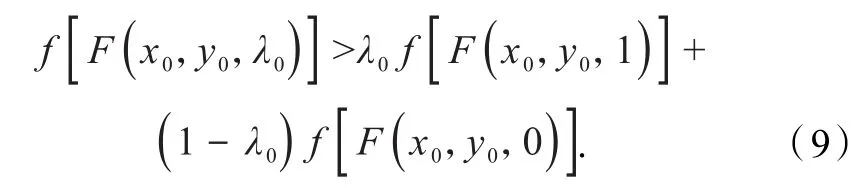
将式(9)改写

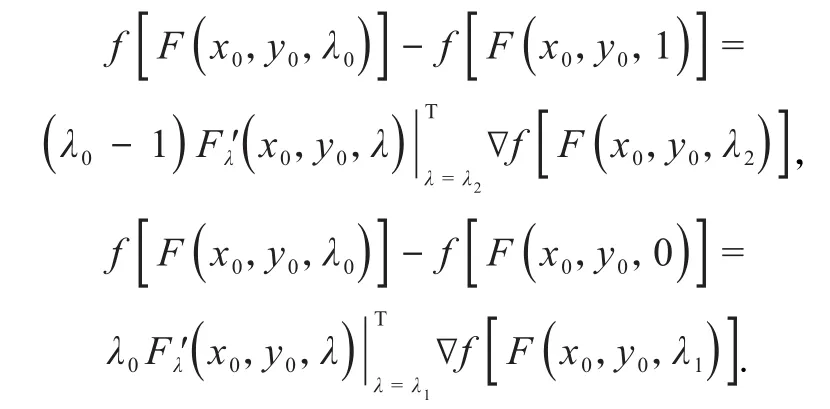
由引理2计算可得
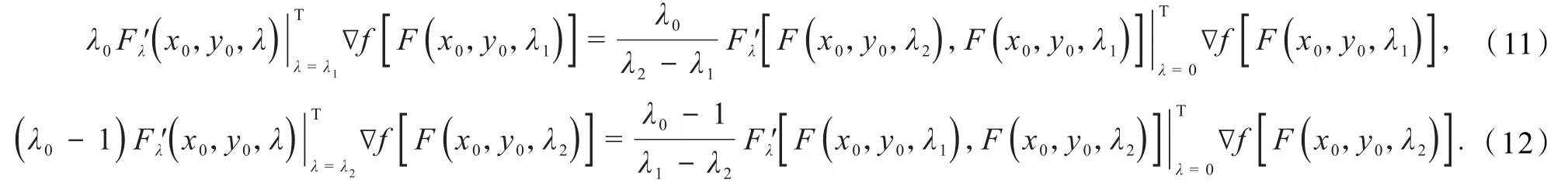
将式(11~12)代入式(10),得
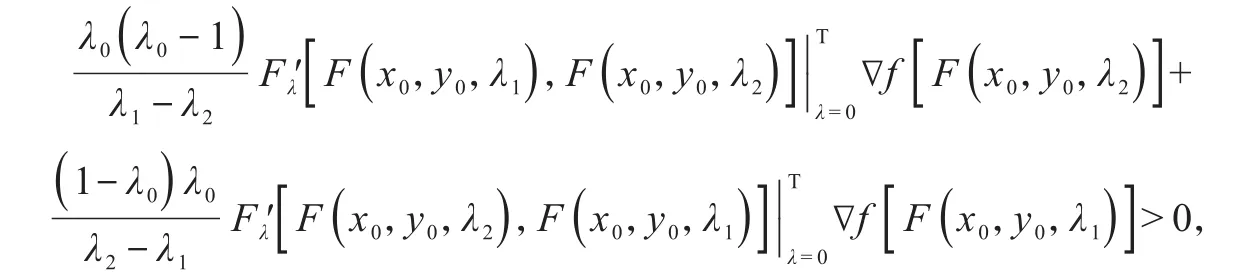
即
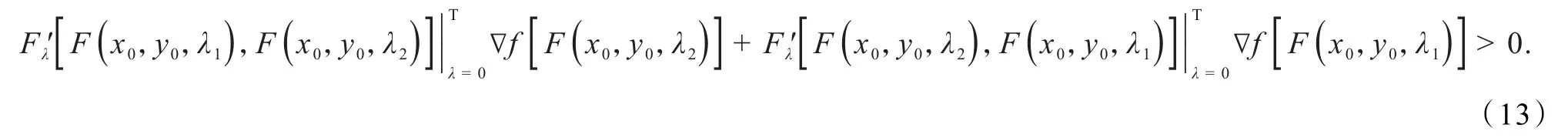
与∇f是K上的F单调映射矛盾.
定理2 设K⊆Rn是关于F的开凸集,实值函数f:K→ R 满 足 :∀x,y∈K有且F关于λ在[0,1]上可微,f:K→ R在K上可微,则f是K上的F伪凸函数,当且仅当∇f是K上的F伪单调映射.
证明 必要性.由引理1结论(2)知,当f是K上的F伪凸函数时,
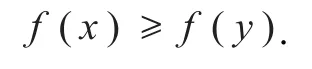
F伪凸函数是F拟凸函数,由引理1结论(3)进一步就有
当f(x)≥f(y)时即 :对x,y∈K且时 ,有所以,∇f是K上的F伪单调映射.
反证法证明充分性.设∇f是K上的F伪单调映射,但f不是K上的F伪凸函数 ,即虽然时,但注意到就 有由 中 值 定 理 ,使
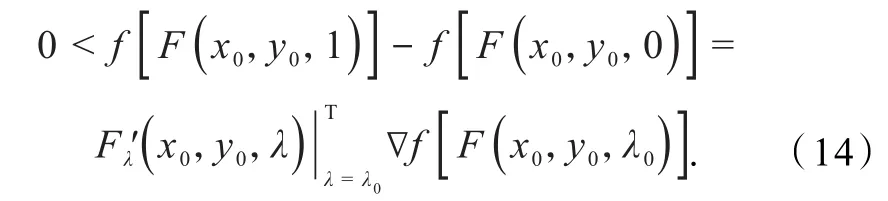
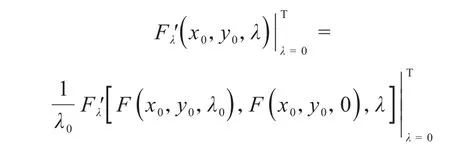
则
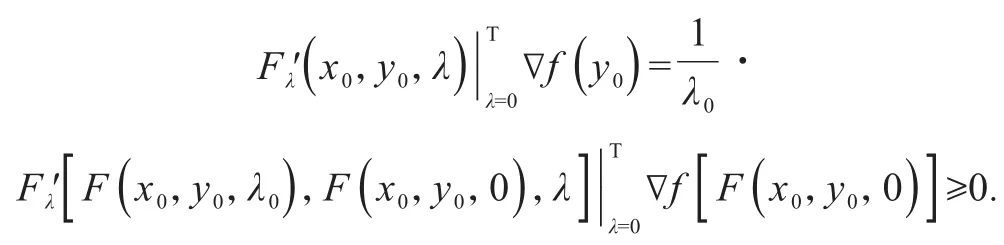
即
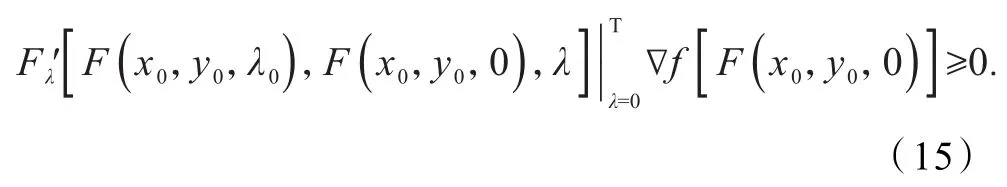
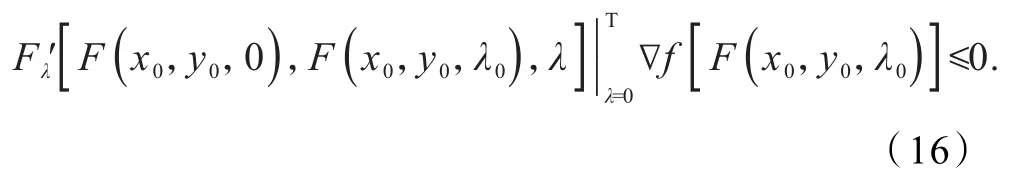
另一方面,由引理2可计算得,
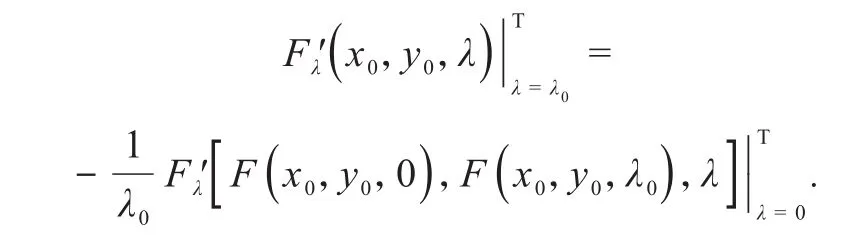
将上式代入到式(14)中得,
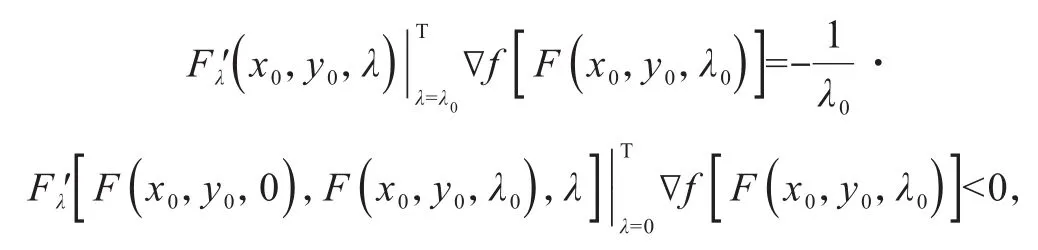
即
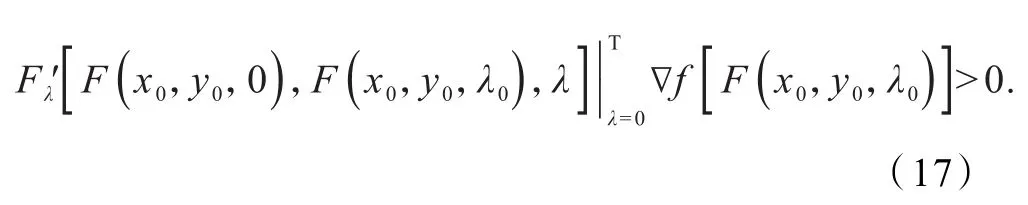
式(16)与(17)矛盾.
定理3设K⊆Rn是关于F的开凸集,实值函数f:K→R满足:∀x,y∈K有且F关于λ在[0,1]上可微,f:K→ R在K上可微,则f是K上的F拟凸函数当且仅当∇f是K上的F拟单调映射.
证明必要性.设x,y∈K且0,由F拟凸性及引理1结论(3)知,进而再由引理1结论(3)就有即当
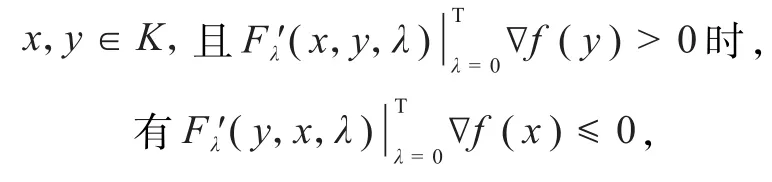
故∇f是K上的F拟单调映射.
充分性.设∇f是K上的F拟单调映射,但f不是K上的F拟凸函数,则
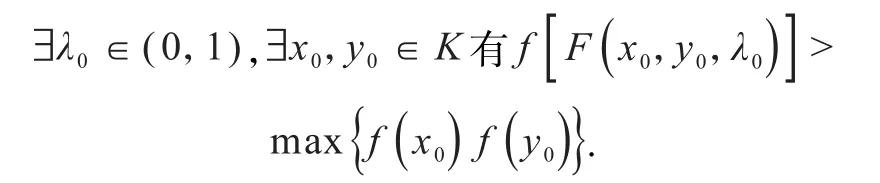
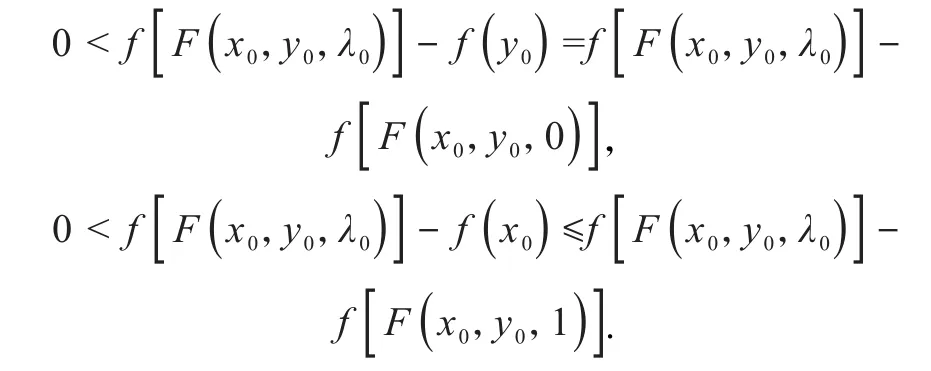
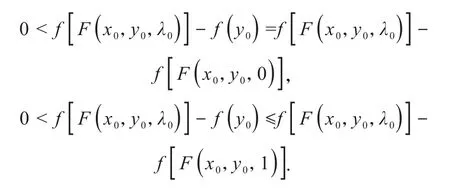
总有
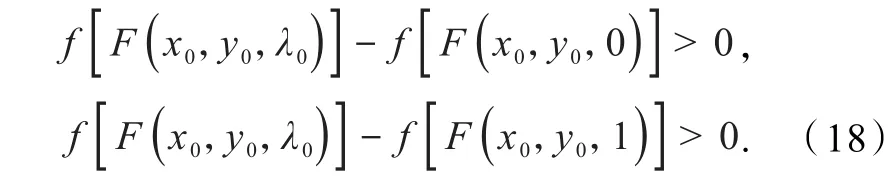
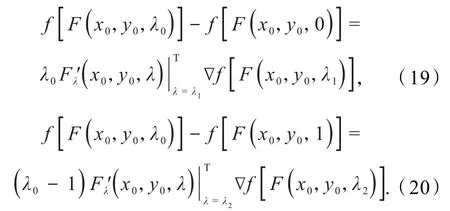
由引理2计算得
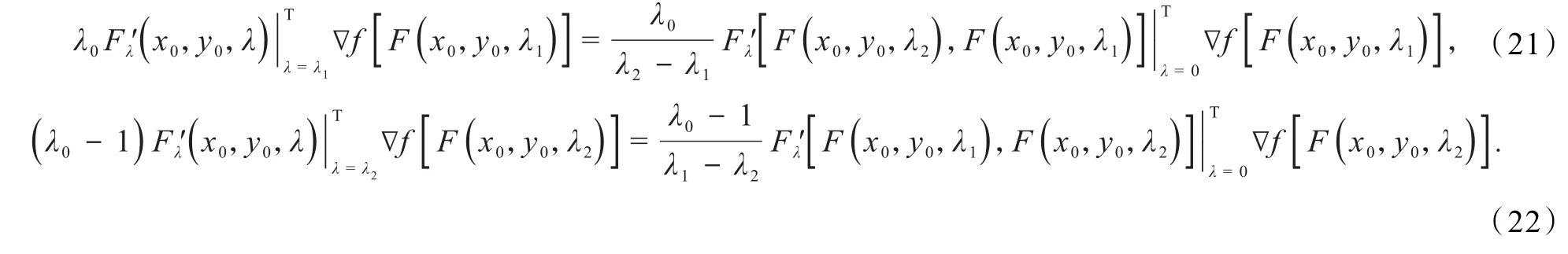
结合式(18~22)有
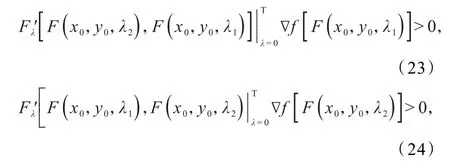
与∇f是K上的F拟单调映射矛盾.
3 应用举例
下面以定理1为例获得一些具体广义凸函数的广义单调性刻画.
定理1指出,在一定条件下,f是K上的F凸函数,当且仅当∇f是K上的F单调映射,即
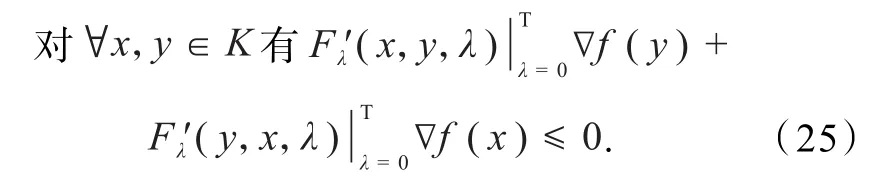
由于预不变凸函数、GA-凸函数分别是特取的F凸函数,相应可求得的形式分别为的相应形式只需将x,y互换.分别代入式(25),可得到一些具体可微广义凸函数的广义单调性刻画,例如关于预不变凸函数的结论[3]:
例1 设K⊆Rn是开的关于η(x,y)不变凸集,且η(x,y)满足条件C,可微实值函数f:K→ R满足且F关 于λ在[0,1]上可微,则f是K上的预不变凸函数当且仅当
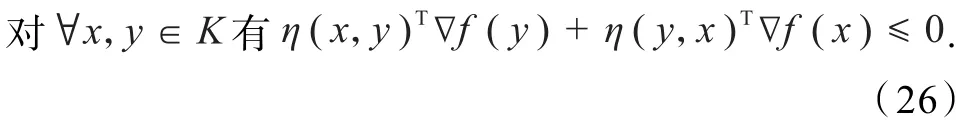
关于GA-凸函数的结论:
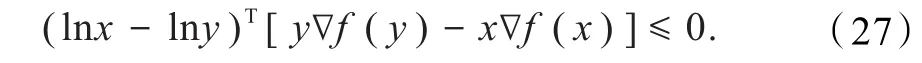
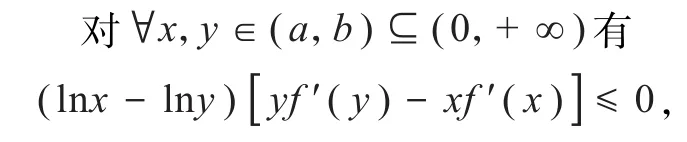
这就意味着xf′(x)为(a,b)上的递增函数.

