考虑轴系扭振抑制的双馈风电机组惯量控制策略

杨苏翔，刘皓明，薛凯旋

（河海大学能源与电气学院，江苏南京 211100）

0 引言

随着风电场并网容量逐步增大，含高渗透率风电的电网实时有功不平衡的问题日益突出，给电网频率调节带来了挑战，也对风电机组频率控制提出了新需求。惯量控制方案能够提高风电机组惯性支撑能力，改善系统频率响应，在实际运行中得到越来越多的关注[1]，[2]。

目前，频率微分辅助（Frequency Derivative Supplementary，FDS）惯量控制方法、频率比例微分辅助（Frequency Proportional-Derivative Supplementary，FPDS）惯量控制方法、最大功率跟踪调整（Maximum Power Point Regulation，MPPR）惯量控制方法在提供动态频率支撑的过程中，存在频率二次跌落、转速恢复慢、频率支撑效果不佳等问题[3]～[9]。

以上惯量控制方法以电网频率为输入信号，直接对有功输出进行调节，使得原本解耦的风电机组轴系转速和电网频率重新耦合，对轴系小干扰稳定性造成影响[10]。文献[11]通过对含惯量控制的双馈风电机组（Doubly-Fed Induction Generator，DFIG）并网模型进行小干扰稳定分析，指出双馈风电机组的惯量控制策略会削弱系统的小干扰稳定性。文献[12]研究了不同的双馈风电机组有功控制策略对其轴系阻尼特性的影响，指出当惯量控制结构和控制参数取值不当时，会导致风电机组轴系的扭转振荡，严重时甚至激发系统低频振荡，威胁电力系统稳定。

本文首先分析了DFIG的惯量控制机理，解析了惯量响应能力和轴系阻尼特性的数学表征，提出惯性阻尼辅助（Inertia and Damping Supplementary，IDS）的DFIG惯量控制方法，进一步通过计算DFIG等效惯性时间常数和轴系等效电气阻尼，建立了含轴系稳定性约束的IDS惯量控制参数整定的数学模型，从而获得IDS惯量控制最优参数，通过对仿真模型的特征根分析及时域仿真，验证了所提IDS惯量控制策略下DFIG惯量响应效果的提升和轴系稳定性的改善。

1 双馈风电机组惯量控制响应能力分析

1.1 双馈风电机组惯量控制

在同步旋转坐标系下，5阶DFIG简化数学模型包括磁链方程、电压方程、转矩方程和转子运动方程[13]。

磁链、电压方程为

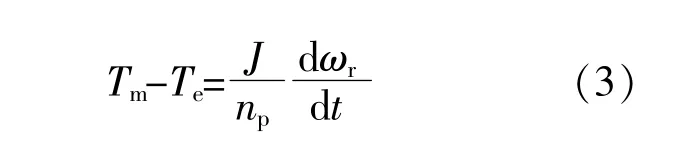
式中:Te，Tm分别为DFIG的输出电磁转矩和输入机械转矩；np为定子绕组极对数；J为DFIG的转子转动惯量；ωr为DFIG转子转速。

将式（2）电磁转矩转化为标幺值，即:

DFIG惯量控制是指当接入的电网频率发生变化时，DFIG通过调整转子转速，改变输出功率，从而对电网提供短时功率支撑[14]。采用上述定子磁链定向矢量控制的DFIG转子侧控制见图1所示。图中:sw为转子转差率；f为电网频率；双闭环控制系统包括功率外环和电流内环。

图1 DFIG转子功率控制框图Fig.1 Rotor active power control of DFIG

目前FDS惯量控制、FPDS惯量控制、MPPR惯量控制均作用于功率外环，如图2所示。

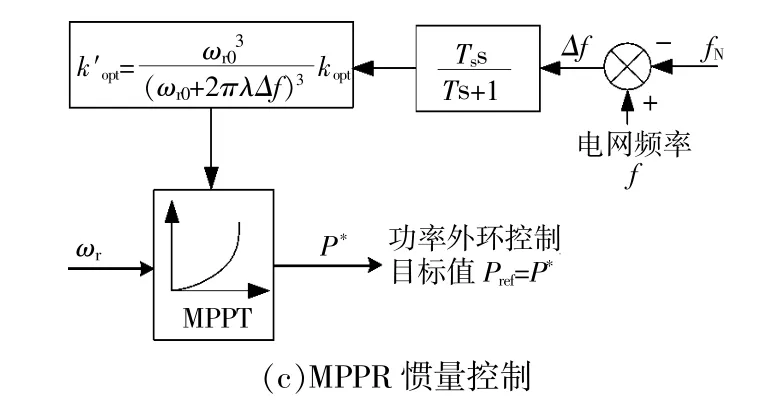
图2 已有惯量控制策略Fig.2 The existing inertia control

1.2 惯量控制下双馈风电机组惯量响应能力分析

各种增加了辅助惯量控制回路的DFIG控制模型如图3所示。其中，求解等效惯性时间常数时将变流器电流内环简化为一阶惯性环节G c（s）=iqr/iqr_ref=1/（τs+1）。

图3 含各种辅助惯量控制的DFIG模型Fig.3 Model of DFIG with supplementary inertia control

当电网频率变化时，DFIG通过改变转子转速来调整有功功率输出，以实现主动惯量响应，其响应能力与其等效惯性时间常数相关。若忽略定子磁链的动态变化过程，并考虑us=φsωs，ωs近似为1，则发电机电磁功率发生变化时满足:

其中，T＜1为低通滤波器参数，FDS惯量控制等效惯性时间常数Heq1会出现为负值的情况，且频率二次跌落程度与T相关，惯量支撑能力与KD/T相关[7]。

同样可以计算FPDS，MPPR惯量控制等效惯性时间常数Heq2，Heq3，从而对相应控制下机的组惯量响应能力进行定量分析，具体的解析表达式为

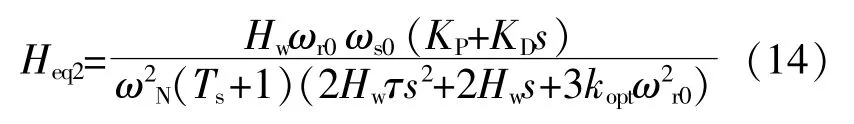
2 惯量控制下双馈风电机组轴系阻尼特性分析

在进行双馈风电机电气阻尼分析时，可以借鉴同步机的转矩分析方法，将电磁转矩分解为同步转矩和阻尼转矩[16]，即:

式中:θ为扭矩角；ω为风电机组轴系的转速差；De为等效电气阻尼系数；ke为等效电气刚度系数。

在图3模型基础上，考虑功率外环中采用的PI控制器的动态过程，同时将电磁转矩视为输出，同时结合式（4），得到转子侧有功控制策略，如图4所示。

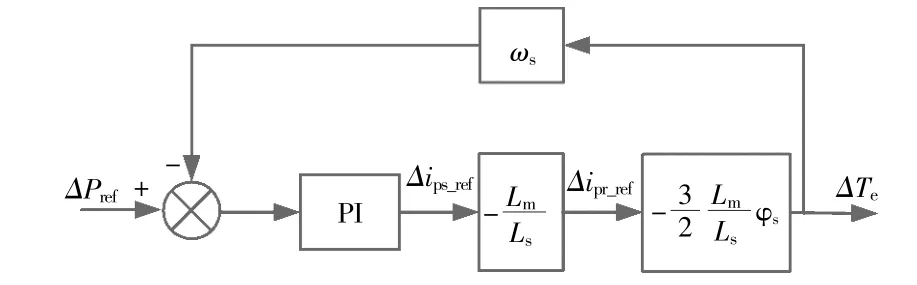
图4 DFIG转子侧有功功率控制框图Fig.4 Rotor side active power control of DFIG

式中:a1=（KP+1.5）2ω2osc+Ki2＞0；b1=3koptω2r0＞0；c1=KP（KP+1.5）ωosc2+Ki2＞0。

由式（19）可知，De＞0，在最大风能追踪控制策略下，电磁转矩提供正的电气阻尼，阻尼系数De的大小与扰动频率有关，当发生轴系扭转振动时，正的电气阻尼会抑制轴系发散振荡[18]。与上节相同，此处也须要对不同惯量响应过程中的有功参考值ΔPref进行计算，但此处关注的是功率变化与转矩之间的关系，为减小计算难度，在本节的计算中不考虑FDS，FPDS惯量控制环节中的低通滤波环节和MPPR控制中的高通滤波环节。下面以FDS惯量控制为例，计算惯量控制策略下的等效电气阻尼系数，以探究风电机组的惯量控制策略对轴系扭振的影响。惯量响应过程中，FDS惯量控制下的电磁功率参考值变化量ΔPref包括ΔP*和惯量控制器输出变化量ΔPD两个部分:

由式（24）可知，等效电气阻尼系数表征了风电机组有功控制系统对轴系振荡的抑制能力，与无惯量控制的情况相比，在FDS惯量控制策略下，等效电气阻尼系数De1中出现了负数项，即当FDS惯量控制参数取值不当时，可能出现De1＜0的情况，此时，电磁转矩提供负电气阻尼。当发生轴系扭转振动时，负电气阻尼会加剧轴系发散振荡。FPDS，MPPR惯量控制下的轴系等效电气阻尼De2和De3分别为

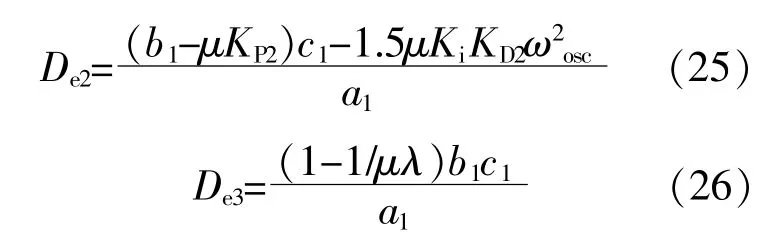
因此，在设计DFIG惯量控制方案时，不仅要关注惯量支撑效果的改善，还须要考虑避免对机组轴系阻尼产生负面影响。

3 IDS惯量控制策略

3.1 IDS惯量控制框架

为了使DFIG具备惯量响应的能力，对式（2）进行调整:

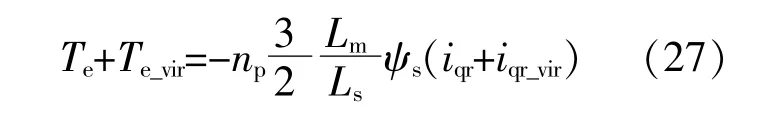
式中:Te_vir为附加的虚拟同步转矩，用于实现惯量控制，同时为轴系附加正阻尼；iqr_vir为Te_vir对应的转子电流q轴分量。

DFIG惯量控制是通过增加以电网频率为输入的辅助控制环节，使机组输出功率相应增加或减少。DFIG附加阻尼控制是通过以发电机转子转速为输入的阻尼器，使转子的自阻尼增加。式（27）中，新增的iqr_vir用于虚拟出DFIG的惯量和阻尼特征，实现风电机组对于所并电网频率变化的抑制作用，同时改善机组的阻尼特性。因此，iqr_vir的输入信号中应当包含电网频率f和发电机转子转速ωr（转差率sw），考虑到DFIG稳定运行时，电磁转矩近似与转差率sw成正比，利用转差率来控制电磁转矩，可实现平滑而稳定的调速效果[20]。对电磁转矩增量Te_vir采用转差率控制，并将其应用于基于定子磁场定向的矢量控制框架中，有:

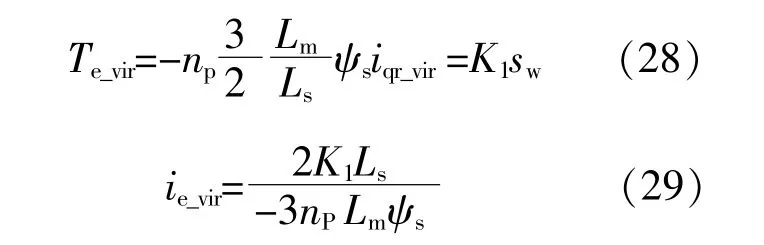
式中:K1为与电机本身参数相关的常数。

利用DFIG转差率信号sw对式（28）中转子电流q轴分量进行控制，控制环节采用PD调节器，则可得:

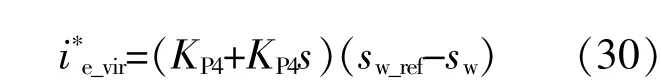
式中:KP4，KD4为PD调节器控制参数；sw_ref为电网同步角频率的标幺值。

IDS惯量控制如图5所示。其中，转子电流q轴分量给定值iqr_vir取为

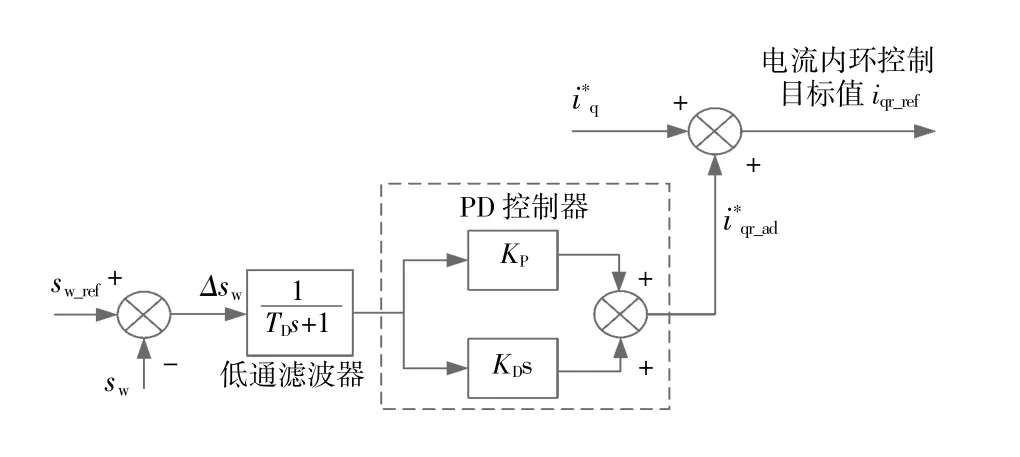
图5 基于转差率反馈的惯量控制Fig.5 Diagram of IDS inertia control

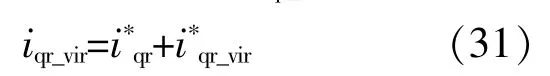
各惯量控制方案中，参数的取值是影响其对轴系的稳定性的关键，所以有必要对IDS惯量控制方案的控制参数进行整定。

3.2 IDS惯量控制参数整定

为获得良好惯量控制效果，改善轴系的阻尼特性，在确定IDS惯量控制参数时，须要综合考虑其惯性时间常数Hdq4和轴系等效电气阻尼系数Hq4，可按前文的方法计算得到，IDS惯量控制等效惯性时间常数为

考虑到IDS的两个待定惯量控制参数KP4，KD4，最优参数选择数学模型为

式中:不等式约束h（KP4KD4）≤0，包括各参数取值范围约束和惯量控制下轴系阻尼大于无惯量控制下轴系阻尼约束。

轴系扭转振动时，正电气阻尼会抑制轴系振荡发散，正电气阻尼越大，抑制作用越强，其约束条件为

与无惯量控制时的等效电气阻尼系数相比，De4是增加的，即y＞0。

IDS惯量控制参数整定是一个有约束的最优化问题，可通过求解得到最佳控制器参数。图6为KP4，KD4不同取值下，轴系等效电气阻尼De4变化。

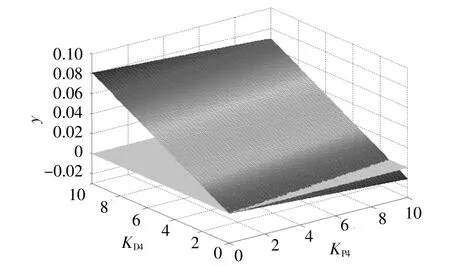
图6 y=f(K P4，K D4)Fig.6 Diagram of y=f（K P4，K D4）

由图6可知，为了保证y尽可能大，KD4在其范围内应取尽量大，KP4在其范围内应取尽量小。

4 算例分析

在DIgSILENT中搭建风电场经输电线路接入电网的仿真模型，如图7所示。单机60 MW的DFIG由30台容量为2 MW的机组等效组成，经出口变压器升压至20 kV、再经升压变压器升至110 kV接入无穷大电网。

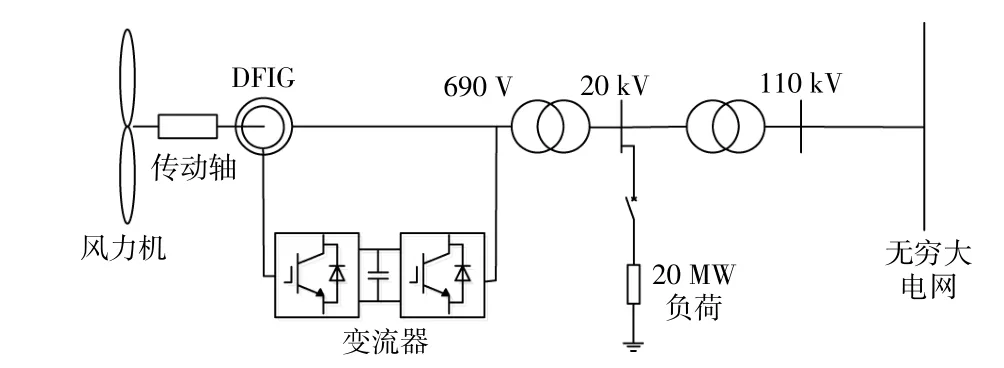
图7 双馈风电机组并网系统Fig.7 DFIG grid-connected system

模型中系统基准频率为50 Hz，基准电压为0.69 kV，基准功率为60 MW。风力机、双馈风电机组的参数设置见表1，2。

表1 风力机参数Table 1 Parameters of turbine

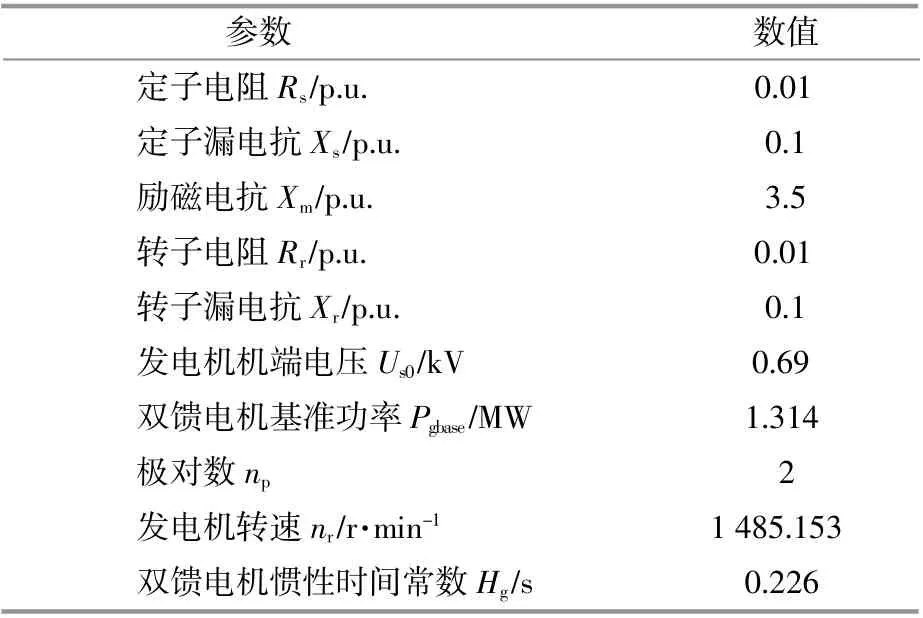
表2 双馈风电机组参数Table 2 Parameters of DFIG

在该模型中，双馈风电机组的轴系采用两质块模型，可计算得出轴系的自然振动频率为[21]

4.1 特征根分析及参与因子计算

系统复共轭特征值的实部对应系统对该振荡模态的阻尼，虚部对应其振荡频率[23]，而系统状态变量关于某特征值的参与因子，刻画了该状态变量对于该特征值下振荡模态的相关性。为分析DFIG惯量控制策略对风机轴系稳定性的影响，在转子侧变流器中分别加入上述的4种惯量控制方法，通过对系统特征矩阵进行特征值分析，得到特征值和参与因子如表3，4所示。其中，各控制参数取值分别为FDS惯量控制参数KD1=30，T=0.1 s；FPDS惯量控制参数KP2=90，KD2=6，Ts=0.1 s；MPPR惯量控制中λ=6，Ts=6 s；IDS惯量控制参数KP4=0.2，KD4=1.8 s。

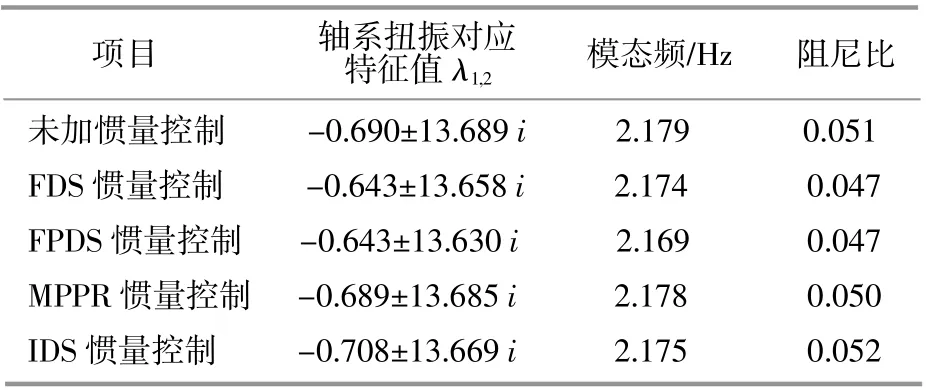
表3 轴系扭振对应特征值Table 3 Comparison of eigenvalues corresponding to the shaft torsional vibration

由表3可知，状态变量中轴系扭转角Δθgt和发电机转子转速Δωg，对特征值Δθgt下的振荡模式起主导作用；对风力机转速Δωt和转子侧变换器中有功控制环相关因子也具有一定作用，该振荡是由于阻尼不足导致的一种机电振荡模式。

结合表3，4可得，与未加惯量控制时相比，FDS惯量控制的加入导致轴系扭振对应特征根的实部向右半平面移动了0.047，阻尼比下降了0.004。FDS惯量控制下，轴系扭转角Δθgt、发电机转子转速Δωg、风力机转速Δωt和转子侧变换器中有功控制环的相关因子，参与了轴系扭振模态，锁相环输出相位ΔδPLL和FDS控制环节引入的状态变量ΔxSFD也对轴系扭振模态有一定作用，这表明FDS环节的加入在一定程度上会加剧轴系的扭振现象。FPDS惯量控制下特征根变化情况及参与因子分布与FDS惯量控制下类似。MPPR惯量控制下特征根实部同样增大了，但增加量非常小，对应阻尼比下降了0.001，MPPR控制环节未给并网系统新增状态变量，但由于其引入了电网频率，锁相环的输出相位ΔδPLL也参与了轴系扭振模态，幅值非常小，近似为0。IDS惯量控制下特征根实部向左移动了0.018，对应阻尼比增加了0.001，同时，由表4可知，IDS惯量控制虽然向系统引入了新的状态变量，但该变量的参与因子非常小，相较于其他状态变量的参与因子，其参与度几乎为0，并未促进机组轴系扭振过程。

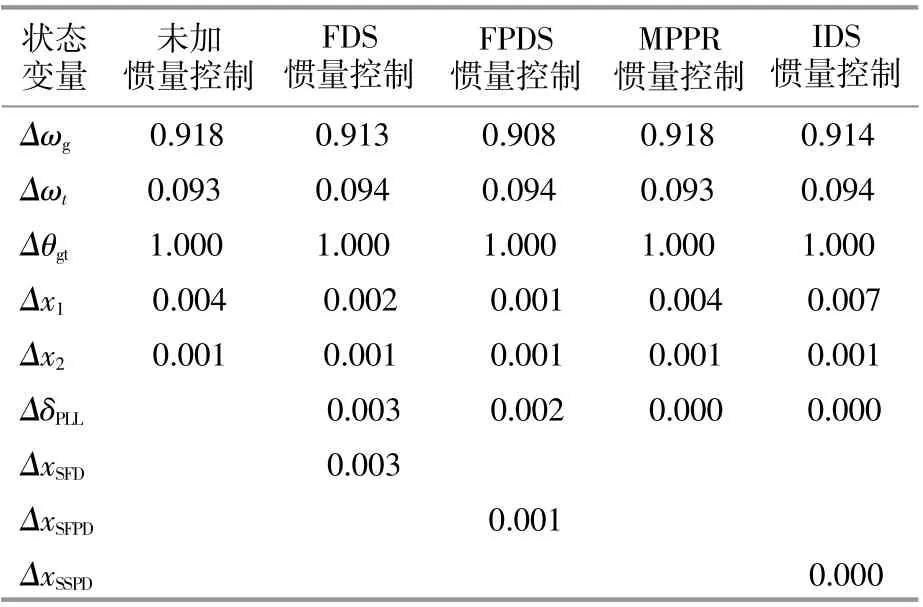
表4 轴系扭振对应特征值下参与因子Table 4 Participation factor analysis of eigenvalues corresponding to the shaft torsional vibration

由此可知:FDS，FPDS惯量控制均使轴系稳定性变差，MPPR惯量控制对轴系稳定性存在负面影响，但影响不大；IDS惯量控制下，轴系稳定性有所改善。特征值分析的结果与DFIG等效电气阻尼计算的结果一致，验证了本文等效电气阻尼解析式的有效性。

4.2 时域仿真分析

仿真中风速额定为11 m/s。为对惯量支撑效果进行比较，设置在0.4 s时，20 kV母线处负荷突增20 MW，造成电网频率下降。仿真得到频降响应曲线，结果如图8所示。

图8 频降响应曲线Fig.8 Frequency drop curve

由图8可知，与未采用惯量控制结果相比，采用不同惯量控制策略，在频率下降偏差、频率二次跌落、转速恢复等关键指标上均有较大影响。其中，FDS和FPDS惯量控制均能显著改善频率下降深度，但却不同程度出现频率二次跌落现象；IDS惯量控制改善频率下降效果最佳，频率响应曲线没有超调，这是因为采用转差率作为控制变量的原因。

进一步观察负荷突增时轴系的动态响应曲线，如图9所示。

图9 轴系扭矩动态响应Fig.9 Dynamic response of shaft torsional torque

由图9可知，FDS惯量控制和FPDS惯量控制的加入使得双馈风电机组轴系的扭矩振荡幅值分别增大了11%，9%，MPPR惯量控制下轴系扭矩增幅不大，近似与未加惯量控制时相等，而IDS惯量控制下轴系扭矩振幅减小。这表明风电机组中附加FDS惯量控制和FPDS惯量控制策略后，会降低其轴系的稳定性，减小原有的机组阻尼，使得扭矩增大，而IDS惯量控制能够提高轴系稳定性，有益于抑制轴系的扭转振荡。IDS惯量控制策略能够在系统频率变化时有效减小频率偏差，同时避免了频率二次跌落现象的发生，且风电机组转子转速恢复较快，具有更佳的轴系扭振抑制效果。

5 结论

本文从改善惯量响应效果和轴系稳定性两个方面出发，对改进的DFIG惯量控制策略进行探究，提出了基于转差率反馈的惯量控制框架；结合等效惯性时间常数和轴系等效电气阻尼计算方法形成参数优化整定的数学模型求解得到所提IDS控制策略最优参数；最后通过特征值分析及时域仿真进行验证分析，得到以下结论。

①风电机组惯量控制方法的惯量支撑能力及轴系扭振抑制效果与控制方法的控制参数密切相关。

②现有风电机组惯量控制方法使得轴系等效电气阻尼为负，所以不利于轴系扭振的抑制。

③在本文所提的IDS惯量控制策略下，DFIG不仅良好地响应电网频率的变化，机组轴系的扭转振荡也得到了有效地抑制。

本文所做的研究基于风速恒定的情况，未考虑极端的高风速/低风速条件，考虑全工况的风电机组综合调频控制策略仍值得进一步研究。