“分块矩阵”思想在高等代数中的应用*——以循环行列式为例

孔祥军， 王 蓓

(①阜阳师范大学数学与统计学院，236037，安徽省阜阳市；② 曲阜师范大学网络空间安全学院，273165，山东省曲阜市)

0 引 言

分块矩阵理论是高等代数的重要组成部分，在分析研究矩阵中有着重要应用，其理论方法渗透在高等代数的各部分内容,其研究已较充分[1,2]. 在高等代数的学习中，对于某些难度较大或理论性较强的问题，应用分块矩阵的理论，可给予较简洁的处理.在此过程中所体现的逻辑的严密性和方法的技巧性，若能仔细体会，则易于理解和把握，从而提高学生的逻辑思维能力和分析问题、解决问题的能力[3-5].

循环行列式是高等代数中的一个非常典型的行列式，其计算或证明体现了行列式理论的严密性和处理问题的技巧性，其难度在常见的行列式的类型中，可以说是最高的，并且具有较广泛的应用. 循环行列式的各种推广得到了广泛研究[6-9].

本文利用“分块矩阵”思想，同时结合行列式的性质，将一类特殊的循环行列式推广到分块矩阵的行列式的情况，得到了一些有趣的结论，丰富和发展了行列式和矩阵的相关理论.

1 预备知识

下面列出本文用到的3个引理.

引理1[3](拉普拉斯定理) 在n阶行列式D中，任取k行或k列(1≤k≤n-1)，由这k行或k列所组成的一切k阶子式与它们的代数余子式的乘积之和等于行列式D.

引理2[3]设A,B是数域上两个同阶方阵，则|AB|=|A||B|.

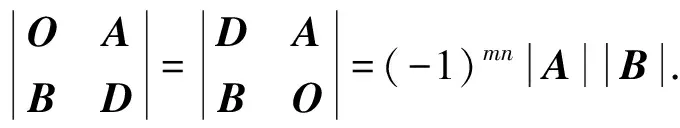
2 主要结果

定理1 设Ai为k阶方阵(i=1,2,…,n)且Ai+1-Ai=C，其中i=1,2,…,n-1. 则

由定理1的结果，可得下面两个推论.

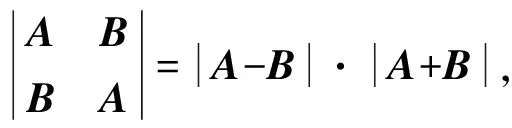
根据分块矩阵思想，由定理1，可以较方便地求出下面的广义循环矩阵的行列式及其逆矩阵.

解由定理1，设A为k阶方阵，则|M|=(-18)k|A|3.

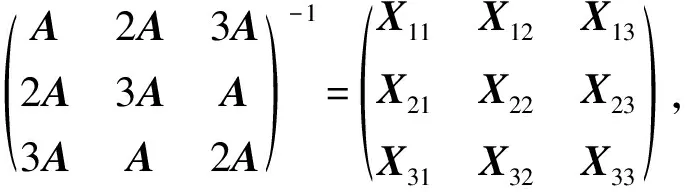
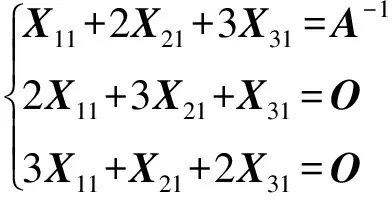
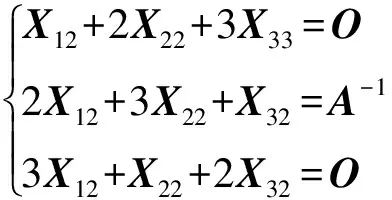
令人感兴趣的是，矩阵M的行列式为广义循环行列式，同样地，M的逆矩阵M-1的行列式也是广义循环行列式.