基于深度神经网络的无环路由算法
高会生,唐 骁,曹旺斌
(华北电力大学 电子与通信工程系,河北 保定 071003)
0 引言
随着云服务、物联网、互联网应用等信息技术和通信产业的快速发展,接入到通信网中的通信设备越来越多,使得网络负载分布不均衡的现象日趋明显[1]。现有的传统流量工程方法,如启发式算法或D算法对流量的控制能力有限。因此,一些基于深度学习的路由算法相继被提出,然而,现有的基于深度学习的路由算法在路径选择时有一定几率产生环路现象,使得这些方法在实际部署时出现困难。所以,在改善传统路由方法带来的拥塞问题的同时,设计一种避免产生路由环路的算法,将会为智能路由研究领域开辟新的道路。
目前在路由优化领域的深度学习方法主要分为2类:深度神经网络(Deep Neural Network,DNN)和与强化学习相结合的深度强化学习(Deep Reinforcement Learning,DRL)。
在DNN方面,文献[2]提出了一种基于DNN的流量工程算法,将请求信息作为神经网络输入,以业务经过链路的概率作为输出,然后用神经网络模型进行路径计算。文献[3-5]将全局网络状态作为DNN模型的输入,将传统算法得到的最优路径作为模型输出来训练模型。部分文献利用卷积神经网络[6-7]或图神经网络[8-9]进行路径计算,能明显改善网络中诸如吞吐量、传输效率等一系列指标的性能。
在DRL领域,文献[10-12]借助DRL技术,提高了网络运行的可靠性和有效性。文献[13-15]提出了一种基于DRL的路由优化选路机制,通过将深度确定性策略梯度(Deep Determinstic Policy Gradient,DDPG)与软件定义网络(Software Defined Network,SDN)技术相结合,优化了SDN的路由选路过程。
DNN和DRL在解决路由计算的问题上各有优劣。其中,相比于传统的最短路径算法,基于DNN的路由算法在诸如传输时延、网络阻塞率等性能上有明显的提升,但随着网络规模的不断扩大,一旦模型出现错误,极易出现路由环路、链路阻塞等严重问题[16]。与DNN不同的是,DRL能够自适应动态变化的网络环境,在路由优化问题上有着良好的通用性与泛化性。然而,当网络规模较大时,DRL模型在训练的探索阶段会产生一些不尽人意的行动,这些行动同样会导致在路由过程中产生路由环路现象,无法继续路由。
目前专门针对避免产生环路现象的相关文献还很少。本文针对上述出现的路由环路问题,提出了一种基于前馈的DNN的无环路由(Loop-free Routing,LFR)算法,并与文献[5]算法进行比较,结果表明本文的算法不会产生环路,且能够改善最短路径算法带来的拥塞问题,对研究方法的可部署性问题有较大的实际意义。
1 相关技术理论
采用前馈的DNN作为后续算法优化的基础。DNN示意如图1所示。 DNN由若干层相互连接的神经元组成,其中第一层为输入层,最后一层为输出层,中间若干层都称为隐藏层。
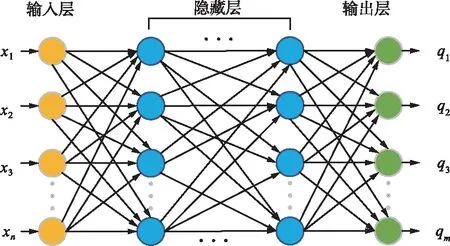
图1 DNN示意Fig.1 Schematic diagram of DNN
DNN中的层与层之间是全连接的,即第k层的任一神经元一定是与第k+1层的任意神经元连接。任意一个输入样本X={x1,x2,...,xn},都有一组输出值{q1,q2,...,qm}与之对应。DNN前向传播算法的计算过程为:从输入层开始,利用每层的权重系数ω与其相连神经元对应的偏置b和输入向量X进行一系列线性运算和激活运算,并且将上一层的输出作为下一层的输入,由前向后逐层计算,直至输出层得到输出结果。
使用前向传播算法计算出DNN模型的输出后,使用损失函数表征模型输出和真实训练样本输出之间的误差。
DNN的损失函数多用均方误差(Mean-Square Error,MSE)来表示,对每个样本,都有:
(1)
式中,qL为模型输出;y为样本的真实输出;k为常数,其值设定与具体实验有关,一般取2。
模型输出和真实训练样本输出之间的误差足够小时,认定DNN模型训练结束,即对损失函数进行优化求极小值,当损失函数达到极小值时对应的一系列权重矩阵W和偏置b即为训练完成的DNN参数。对损失函数逐步求得极小值的数学工具称为优化器。优化器的选择将在后文进行描述。
对于一个合格的DNN模型,应该具备对位置数据的准确预测能力。在训练初始阶段,若DNN模型拟合的函数在训练数据集上拟合得好,但对于测试数据集不适用,此时称模型过拟合。当模型出现过拟合时,往往是因为训练数据中噪声干扰过大、参数太多、模型复杂度过高造成的。因此,一般采取的方法有缩小模型复杂度、降低特征数量和正则化。
2 算法设计
2.1 DNN指标设计
为了保证模型训练过程中不出现过拟合问题,采取一种正则化方法,即早停法(Early Stopping)。该方法将训练数据集分为2部分:训练集和验证集,只将训练集用于模型训练,在每次前向计算与反向传播的过程结束后,在验证集上得出精度结果并记录,当模型在验证集上的精度不再有明显增长甚至减小时,停止训练。
DNN模型的输出以列向量表示。在模型训练结束后,对模型准确率σ进行统计:
(2)
式中,Q为DNN模型的输出向量;H为Q中元素个数;Q0为Q对应的测试真值。设阈值ε=0.1%,若σ≤ε,则认为输出满足要求;否则,不满足要求。
2.2 DNN算法部署方案
当前基于深度学习的路由算法可大致分成2种部署方案:集中式路由方案和分布式路由方案。
在集中式路由方案中,所有路由器与同一个中央控制器相连,中央控制器收集汇总全网拓扑及流量信息,然后通过一个DNN模型做出相应路径计算,将路由方案下发到各个路由器,路由器收到下发信息后完成业务调度。当前大多数集中式智能路由算法都需要以SDN为基础,而SDN主要应用在一些特定的网络场景下,如数据中心网络。因此,集中式路由方案在泛用性上较差。
在分布式路由方案中,每个路由器都有一个专有的控制器与之相连,即每个路由器都要训练一个DNN模型,如图2所示。这些控制器中只包含本路由器及其相邻路由器的路由信息,通过这些信息来选择下一跳路由端口[17],以此完成业务配置。当前通信网仍然以分布式路由为主流的路由协议,本文采用分布式路由的部署方案,旨在与现有网络协议之间有更强的兼容性。
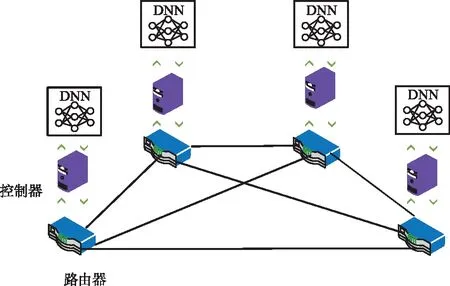
图2 分布式路由方案示意Fig.2 Schematic diagram of distributing type route scheme
2.3 无环路由算法流程
本文提出了一种基于DNN的LFR算法,通过逐跳趋近目标节点的原理进行路由,由上文可知,网络中的每个节点都需要训练一个DNN模型。对通信网的网络拓扑进行建模,由G=(V,E)表示,其中,V表示通信网络中的节点集合,E表示链路集合。
DNN模型的输入为目的节点和链路权重,模型输出为当前节点到所有目的节点的最短路径长度。算法流程如图3所示。
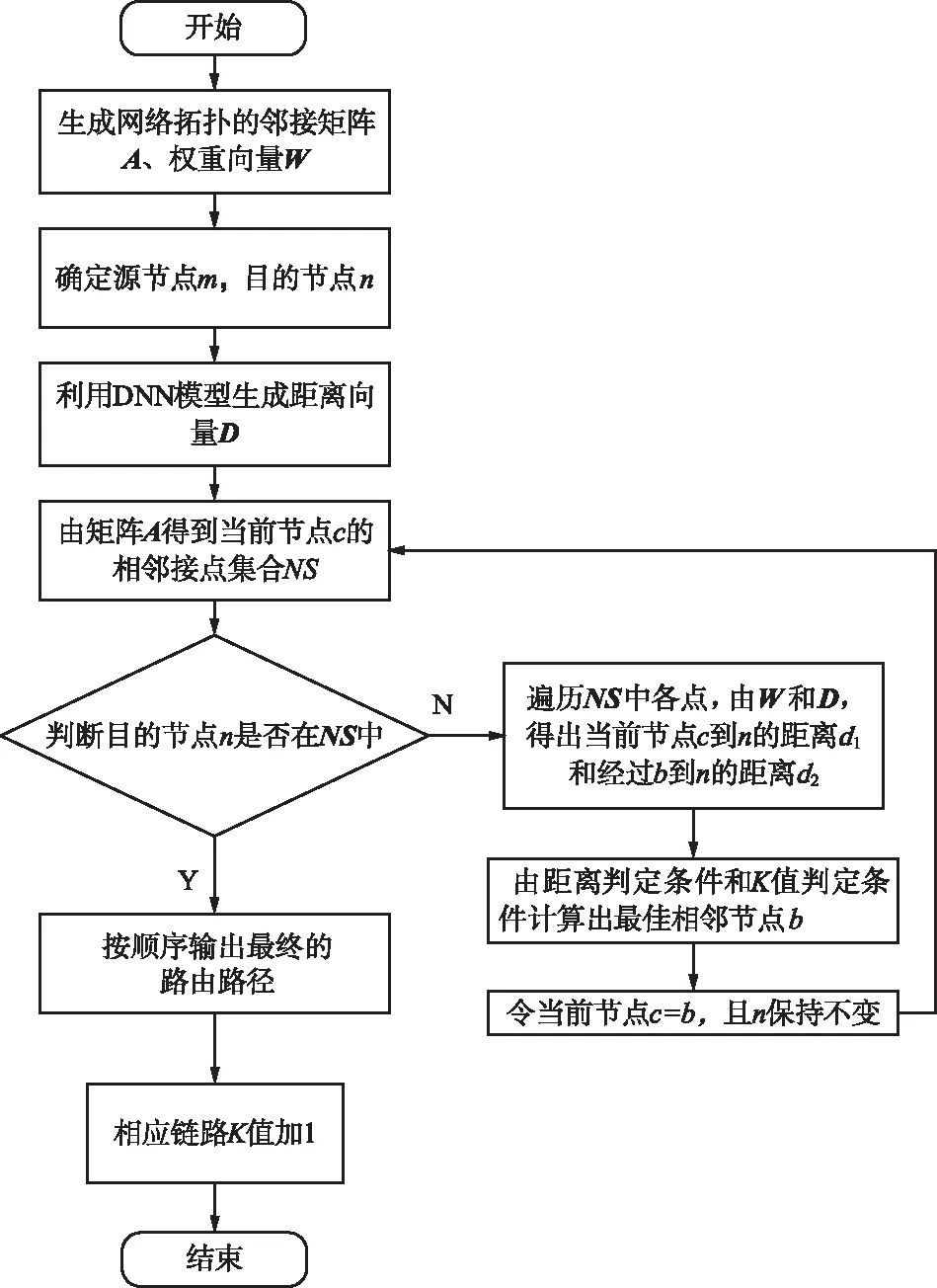
图3 算法流程Fig.3 Algorithm flow chart
(1) 生成网络拓扑的邻接矩阵A,生成权重向量W。其中,A为稀疏矩阵,权重为1。A的元素aij满足如下条件:若(i,j)∈E,则aij=1;否则,aij=0。
(2) 确定源节点m,目的节点n,当前节点c。
(3) 利用DNN模型生成距离向量D,D的元素dj表示网络中各节点到目的节点n的最短路径距离。
(4) 由矩阵A得到当前节点c的相邻节点集合NS[18]。在邻接矩阵A的第m列找到满足aim=1元素,所对应的节点为v1,v2,…,vk,这些点构成m的相邻节点集合,即NS={v1,v2,…,vk}。
查询NS中的各个节点,值得注意的是,先前查询过的节点,在后续的NS集合中不会再出现。若n∈NS,则结束路径计算,最终路由路径为path={m,n};否则,根据链路的权重向量W和距离向量D,计算当前节点m、相邻节点b∈NS到目的节点n的距离,分别记为dmn和dbn。
求距离差值δmb:
δmb=(ωmb+dbn)-dmn,
(3)
式中,ωmb为当前节点m到相邻节点b的权重长度。设定一个合适的阈值α,其取值为:
(4)
式中,N为NS中候选下一跳节点b的个数;η为常系数,满足条件:
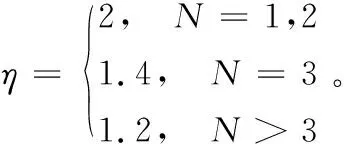
(5)
若满足条件(ωmb+dbn)-dmn≤α,将该相邻节点b保留在NS中;否则,将该节点从NS中删除。若集合NS遍历结束后,NS中存在多个候选节点b,则按如下原则选取下一跳节点:
(6)
式中,向量K中包含的是当前节点m与各候选下一跳节点b之间链路上已承载的业务数量k。比较各链路emb上已承载的业务数量kmb,若k值都相等,则取使得δ值最小的相邻节点b作为下一跳节点,否则选择K中的值最小的节点b。
令当前节点m=NextStep,目的节点n保持不变,从步骤(2)重复此过程,直至n∈NS,按顺序输出最终的路由路径,并更新向量K中相应位置的k值。
2.4 关于LFR算法的几点说明
(1) 当前,环路现象是分布式智能路由算法的一项不可忽视的问题,本算法首先利用距离判定,控制距离差值δ在一个较小的范围内,使节点逐跳逼近目的节点;其次,每次更新相邻节点集合NS时,都会自动删除掉上一跳节点。通过以上2种方式,保证了LFR算法不会产生路由环路。
(2) 多数基于分布式的智能路由算法的神经网络模型是以下一跳端口号为输出,一旦模型出现错误,极有可能产生环路现象或无法获取到下一跳端口,导致路径计算错误,这在实际通信网中应尽量避免。LFR算法将距离值代替端口号作为DNN模型的输出,即使模型出错,算法将以次优路径完成路由选择。
(3) 理论上,最短路径算法可以准确高效地解决单业务的路由问题,然而,当业务量较大时,势必会造成最短路径经过的链路负载过重,甚至造成链路拥塞。因此,考虑到实际通信网中负载均衡的问题,LFR算法每次循环到步骤(4),通过引入阈值α,使得到的经过节点b的路径与最短路径的距离之差在允许的范围内时,将b视为可选节点,在此基础上进一步比较链路上承载的业务数量,以此得到的路径称为可选路径。因此,本算法得出的所有路径并不都是最短路径,而是在保证不产生环路且链路利用较为均衡的前提下,路由的总距离尽可能短。
2.5 算法实例
本文选择7节点网络拓扑为算例说明,如图4所示。某一时刻,网络归一化的链路权重已由图中给出。该时刻网络中各条链路上承载的业务数量如表1所示。
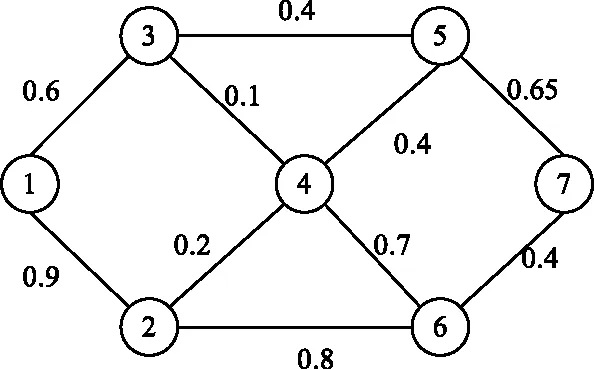
图4 算例网络拓扑Fig.4 Network topology of the example
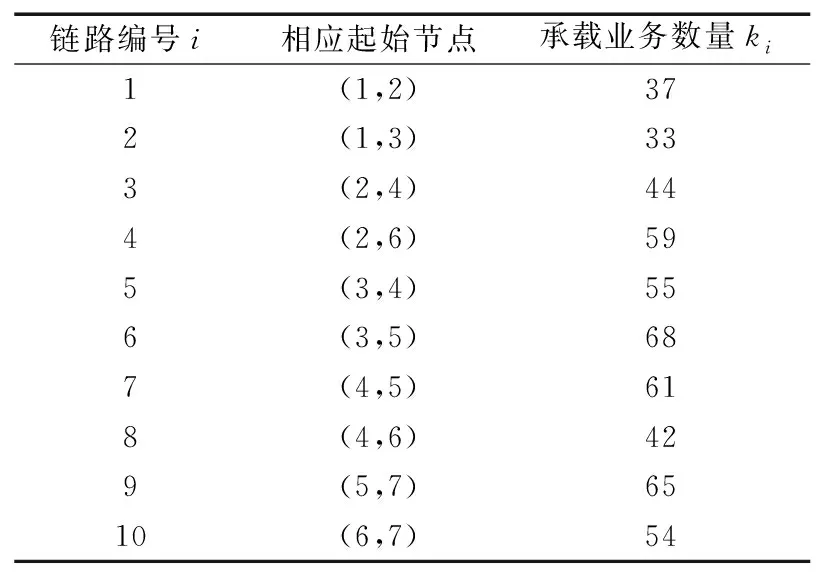
表1 链路编号及已承载业务数量
以上图为例说明本文算法的执行方式。
(1) 首先根据图4,得出邻接矩阵:

(2) 随机产生一个业务,源节点为m=1,目的节点n=7,因此当前节点c=1。
(3) 利用结果训练的DNN模型,计算出距离向量:
D=[1.55,1.4,0.95,1.05,0.65,0.6,0]。
(4) 由矩阵A得出当前节点1的相邻节点集合NS={2,3},检测到7∉NS,继续下一步。
(5) 遍历NS中各个节点,计算:
ω12+d27=ω12+D(2)=2.3,
ω13+d37=ω13+D(3)=1.55,
经计算,α=0.75。
ω12+d27-d17=0.75≤α,符合条件,保留;
根据拟建建筑物特点,结合场地地质条件,可采用天然地基。考虑到场地含一层地下车库,建议挖除第①层表土层、河沟鱼塘处的淤泥和回填土及第②层黏土层,以第③-1层含砂姜黏土作为基础持力层;基础形式建议采用高层筏板基础,多层可采用柱下独立基础及其他符合设计要求的基础形式。
ω13+d37-d17=0≤α,符合条件,保留,
经比较,k1>k2,因此下一跳节点b=3。
(6) 当前节点m=3,更新集合NS中的元素,NS={4,5},检测到7∉NS,继续下一步。
(7) 计算(ω34+d47)-d37=0.1≤α,保留;
(ω35+d57)-d37=0≤α,保留,
经比较,k5 (8) 更新集合NS中的元素,NS={2,5,6},检测到7∉NS,执行下一步。 (9) 计算得α=0.093 8。 (ω45+d57)-d47=0.1>α,NS中删除节点5; (ω46+d67)-d47=0≤α,保留。因此下一跳节点选择6。 (10) 当前节点m=6,更新NS,NS={2,7},检测到7∈NS,因此,下一跳节点为7。 输出路径path={1,3,4,6,7} 向量K中k2,k5,k8,k10各增加1。 本文使用Matlab编写了NLSPR算法。该仿真环境在Ubuntu16.04系统上运行,硬件系统为IntelXEONE5-2680V4CPU,32GBDDR4内存和一块2080Ti显卡。 仿真分为2部分:首先确定合适的DNN模型并评估其性能;其次,从负载均衡和算法运行效率2个角度将本文算法与相关方法进行比较。 DNN的架构是本文算法的重要组成部分,大多数文献在设计DNN的结构时都采用基于经验的方法,本文采用实证的方法设计其结构。DNN结构包括神经网络层数、每层神经元个数和优化器等。 由前文可知,输入特征是目的节点和链路权重,标签为当前节点到所有目的节点的最短路径长度,每个节点都要训练一个DNN模型,本文利用Matlab为每个DNN模型生成数据集,每个训练集包含160 000个训练样本(总样本数的80%)和40 000个测试样本(总样本数的20%)。由于DNN的权重和偏置是通过随机种子算法初始化的,每次训练结果会有所不同,因此将多次仿真结果的平均值作为最终的实验结果。 为了确定出合适的DNN结构,对不同的结构进行仿真,图5为主要的测试数据,描述了DNN训练集和测试集不同的隐藏层层数与每层神经元个数组合下的MSE性能。由图5可知,当每层神经元个数固定时,MSE随着层数的加深,呈现先减小后增大的趋势,因此,隐藏层为5层时,MSE最小;当层数固定为5层,每层神经元个数为20或25时,MSE达到最小,考虑到随着隐藏层的神经元个数增加会使模型训练变得复杂。因此,本文选择5层隐藏层,每层20个神经元的组合作为最终的模型结构。 图5 不同DNN结构下的MSE性能Fig.5 MSE performance under different DNN structures 为尽可能地提高DNN训练集的精度,本文采用4种优化器对DNN进行训练,这4种优化器都是基于梯度下降法演变而来,分别是随机梯度下降(StochasticGradientDescent,SGD)、标准动量优化(Momentum)、均方根支柱(RootMeanSquareprop,RMSprop)和自适应矩估计(AdaptiveMomentEstimation,Adam)。图6显示了4种优化器在DNN中预测出的MSE,可以看出,利用Adam优化器在本文DNN模型训练中的精度优于其他3种优化器。 图6 不同优化器对DNN精度的影响Fig.6 Influence of different optimizers on DNN accuracy 针对各项性能指标将本文的LFR算法与文献[5]算法进行负载均衡和运行效率两方面对比。 文献[5]提出的分布式路由算法中,将全局的网络权重矩阵作为DNN模型输入,将传统最短路径算法得到的下一跳节点作为输出。 本文选取某地区真实电力通信光网络拓扑进行实验(包含61个节点、91条链路),拓扑图如图7所示。 图7 某地区电力通信网拓扑Fig.7 Power communication network topology in a region 首先从负载均衡的角度进行实验,定义单个链路的资源利用率如下: (7) 式中,M为通过该链路的业务数量;qi为不同种类业务占用的带宽容量;C为该链路的链路容量。为简化实验,随机生成1 000个业务请求,即业务请求的源节点、目的节点都是随机的。设置每条链路的最大容量为300,每条业务所占链路容量相同,设为1,对文献[5]算法和LFR算法进行仿真对比实验。 图8为所有业务配置完毕后,2种算法的链路利用率对比图。从仿真结果可以看出,由于文献[5]算法的DNN模型是基于最短路径算法训练的,所以整体链路负载分布并不均衡,少数链路的资源利用率甚至达到95%以上,而大多数链路的资源占用率都在20%以下,即随着业务请求量的增多,该算法极有可能形成链路拥塞。而LFR算法的多数链路的资源利用率在20%~50%,最大资源利用率不超过60%。因此,LFR算法能够有效地提高资源利用率,改善最短路径算法在负载均衡问题上的不足。 图8 链路利用率对比Fig.8 Comparison diagram of link utilization 在算法运行效率方面,定义业务配置完成时间为: Tcomplete=Ta+Tl+Tq, (8) 式中,Tcomplete为业务配置完成时间;Ta为算法进行路径计算的时间;Tl为路由经过的链路时延之和;Tq为拥塞时业务的等待时间。设置每条链路的最大容量同样为300,每条业务占用容量为1,按照实际设置该电力通信网链路长度,规定数据在单位长度光纤内传播速率为0.005 25ms[19],业务请求按周期为0.01ms随机生成,通过不断增加业务请求量,统计业务配置的完成时间。 多次配置同样数量的业务求得的业务配置完成时间的平均值如图9所示。 图9 业务配置完成时间对比Fig.9 Comparison chart of business configuration completion time 当业务请求量较少时,文献[5]算法与LFR算法有着相似的性能,甚至文献[5]算法的运行效率更好,这主要是由于,相比本文算法,该算法没有多余判定条件,并且在业务请求量少时,链路资源充足。然而,随着业务量的持续增长,文献[5]算法开始出现排队拥塞,少数业务路由时甚至会产生环路现象,导致业务配置时间持续增长。相比之下,LFR算法在传输时延方面表现相对较好,这是由于LFR算法在保证不出现环路现象的前提下,权衡了路径与链路利用率关系,在一定程度上减轻了最短路径相关算法容易产生链路负载过重的压力。 本文提出了一种基于DNN的无环路由算法,通过相关节点控制与距离判定的方式,逐跳趋近目标节点,解决了当前智能路由算法有可能产生环路现象的问题。通过引入链路业务承载量的判定条件,使链路利用率较为均衡。同相关智能路由算法相比,在配置相同业务数量的情况下,本文算法在负载均衡和运行效率方面均有良好表现。为真实场景中智能路由算法的安全性和可靠性问题提供了重要的参考价值。 未来的工作,将考虑在更大的网络规模和更多约束条件的情况下进行研究,进一步提升算法性能。3 实验验证
3.1 实验环境
3.2 模型训练及评估
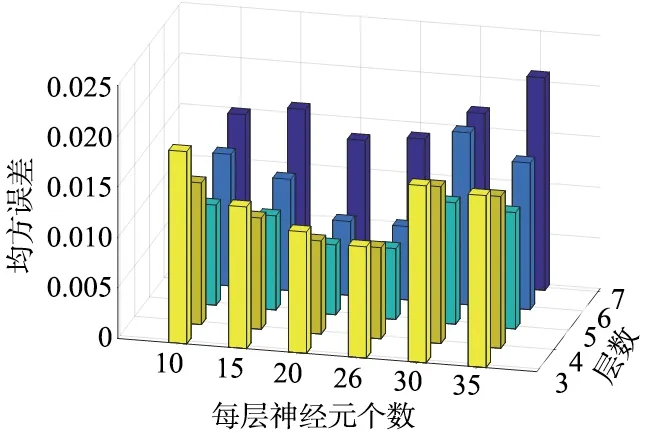
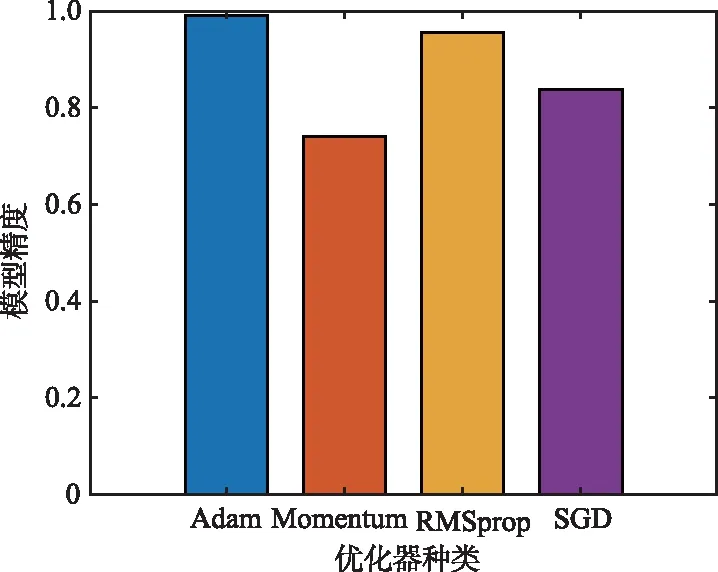
3.3 算法性能评估
4 结束语

