基于数学运算素养的一道联考题的思考
胡春香 李连方 (浙江省湖州中学 313000)
1 思考背景
数学教学已经进入“核心素养”时代,高考试题也在发生新的变化,侧重考查学生自主探究解决问题的能力,这对师生提出了更高的要求.《普通高中数学课程标准(2017年版)》指出,数学运算是指“在明晰运算对象的基础上,依据运算法则解决数学问题的素养”,主要包括理解运算对象、掌握运算法则、探究运算思路、选择算方法、设计运算程序、求得运算结果等.运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力.众所周知,解析几何的本质是用代数方法研究几何问题,它把曲线用代数形式表示,利用代数形式研究几何性质,研究各种位置关系和数量关系,是培养学生运算求解能力的重要载体.本文通过一道解析几何试题的解析,谈在教学中如何培养学生的数学运算素养.
2 问题呈现
(2021年浙江协作体高二数学返校考)如图1,已知过抛物线C:y2=4x焦点F的直线交抛物线C于点A,B(点A在第一象限),线段AB的中点为M,抛物线C在点A处的切线与以AM为直径的圆交于另一点P.

图1


这是一道以阿基米德三角形为背景的综合性解析几何问题,主要考查直线与圆锥曲线位置关系的综合应用,涉及到抛物线的定义、圆的方程、弦长公式及其垂直距离的求解等知识点,考查学生的数学运算能力和数学转化能力.该题融多种数学思想方法和解法于一体,对学生的计算能力有着较高要求,是一道有一定难度的题目(整个年级的该题得分率仅为32%).
3 如何培养学生的数学运算素养
3.1 回归本质,确立运算思路



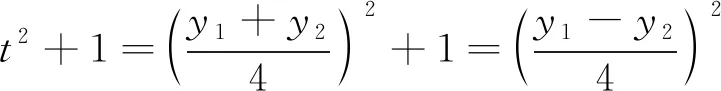
反思 确定思路1后,教师更重要的是引导学生选择合理的运算法则,设计合理的运算程序.后续的消参化简有一定的难度,需要教师适时引导学生合理地利用韦达定理的两个等式.
3.2 巧借向量,优化运算方法



反思 解决解析几何中的垂直距离的方法有很多,而向量是解决垂直距离的最优方式,能实现运算的优化.本解法就是利用有关向量坐标的确定,结合投影的本质,巧妙地借助向量的坐标运算转化了圆锥曲线问题,从形入手转化为数的运算,简化了运算,很好地培养了学生的数学运算素养.
3.3 巧设参数,提升运算效率


图2

反思 解析几何问题的解决关键在于设参与消参.在其运算过程中,及时地审视与反思从而调整运算策略,这有助于提升学生运算的正确率和速度.本题在利用点参运算复杂时,转而利用倾斜角为参数大大简化运算,从而有效地提升了学生的数学运算素养.
3.4 重视背景,提高思维能力
将几何问题代数化是解决解析几何问题的基本思路,但是若合理地利用几何背景,揭示问题的几何本质,可以极大地简化运算过程,提高学生的思维能力和品质.

图3

总而言之,学生的运算素养是可发展、可提升的.课堂教学要以培养学生的运算能力作为教学目标之一,做好每一节课的教学设计,把提高学生的运算素养渗透到每一节课中.在问题的解决过程中,重视引导学生思考:“为什么要这样算,是否有更好的运算方法.”将教师精心选编的每一道例题中蕴含的数学运算方法合理和自然表现出来,反复强化和渗透,将其始终贯穿课堂的教学中,学生势必会形成良好的运算习惯,数学运算素养必定能大大提升.

