考虑多类型产品新鲜度的生鲜配送路径优化

酒艳妮，胡大伟 （长安大学运输工程学院，陕西 西安 710064）

0 引 言

随着社会经济水平的不断提高，消费者对于水产品、果蔬、鲜肉产品等生鲜产品的需求与日俱增。新冠疫情的爆发改变了人们的消费方式和饮食方式，加快推动了消费者对健康食材产品的需求，消费场景化趋势更加明显。消费者线下到店购买频率降低，转到线上购买，生鲜电商在此期间蓬勃发展。由于生鲜食材的易腐性，消费者对其配送过程有着较高的要求。同时消费者的生活习惯等的差异，使其对偏好种类等产生不同，生鲜食材企业如何满足客户对不同种类生鲜的需求，优化生鲜食材配送网络，提高服务质量和配送效率，同时降低成本，成为亟待解决的问题。

在生鲜配送方面，冯杰等人在纯电动冷藏车生鲜配送路径优化中考虑电动车到充电站充电及客户软时间窗约束，并设计蚁群算法进行求解；娄晶等考虑现实生活中城市道路交通的时变性和生鲜配送的时效性，以最小使用车辆数和最少行程时间为优化目标，构建了时变路网下带硬时间窗的生鲜物流配送路径选择模型；方文婷等人将绿色发展理念考虑在冷链配送路径优化中，建立以固定成本、绿色成本、制冷成本、货损成本、时间窗惩罚成本最小为目标函数的冷链配送数学模型采用混合蚁群算法求解；王勇等人以运输成本、温控成本、违反时间窗的惩罚成本最小化及生鲜价值损失最小为目标，考虑商品温度控制和时间窗约束建立了生鲜配送优化模型，用混合遗传算法进行求解；赵志学、李夏苗基于时变路网的特点，同时考虑电动车电池电量约束、车辆容量约束、生鲜新鲜度约束等构建优化模型，并设计自适应改进蚁群算法求解；余建军等研究生鲜外卖配送中最小化配送成本和最大化顾客满意度，通过自适应算法改进遗传算法求解优化模型。曹文彬等人考虑了新鲜度惩罚，提出变领域搜索改进遗传算法进行求解；目前国内对生鲜配送路径优化领域的研究丰富，多从生鲜配送过程中涉及到的成本，特别是生鲜新鲜度和配送温度控制方面及生鲜配送的时效性进行研究，且多为单品种生鲜配送网络。

本文针对客户对多类型生鲜产品的需求，综合考虑不同类型生鲜产品在配送过程中的新鲜度变化，考虑不同的保鲜制冷方式，差异化新鲜度敏感系数，引入生鲜保鲜努力系数，产生相应的制冷成本和货损成本，同时结合客户对生鲜配送的时效性要求，考虑配送时间窗约束，建立生鲜配送数学模型，并设计混合遗传—粒子群算法进行求解。

1 问题描述与模型构建

1.1 问题描述

考虑到实际中客户对不同生鲜产品的需求偏好，生鲜配送过程不同产品保鲜方式不同新鲜度衰减不同，本文研究的考虑多类型产品新鲜度的生鲜配送路径问题描述如下：

在一定城市区域内，客户通过生鲜电商下单，由生鲜电商在该区域内的配送中心或前置仓为其提供配送服务。每个客户的地理位置已知，对于不同种类的生鲜产品需求已知，对配送服务的时间窗已知。生鲜产品包括常温、冷藏、冷冻三类，对于不同的产品在配送过程中采用不同的保冷方式。配送中心利用自有车辆，利用泡沫箱、冰袋及小型冷冻箱等对常温、冷藏和冷冻生鲜产品进行配送，受服务时间窗和车辆容量限制等的影响，合理规划配送路线，在固定成本、运输成本、货损成本、制冷成本、违反时间窗的惩罚成本最小的情况下，完成客户配送服务。

1.2 基本假设

考虑到实际问题的复杂性，本文做如下假设：

（1） 客户点位置、时间窗及与配送中心的距离已知；

（2） 客户对不同种类的生鲜需求已知；

（3） 配送中心的车辆为同质车辆；

（4） 车辆匀速行驶；

（5） 车辆从配送中心出发并返回原配送中心。

1.3 参数说明

表1 参数和定量定义

1.4 模型建立

1.4.1 成本分析

①车辆的固定使用成本

车辆的固定使用成本主要是指车辆被启动所产生的一系列的固定成本，记为Z。

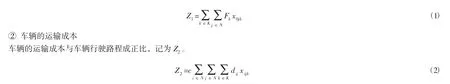
③制冷成本

本文研究的生鲜配送路径优化中，生鲜产品包括三种类别：常温、冷藏、冷冻。对于生鲜配送最后一公里问题，考虑到城市道路限制、客户需求量小且分散的特点，采用电动车辆为客户进行配送。对于常温产品，在配送过程中不采取制冷措施；对于冷藏产品，一般使用冰袋、冰包等；对于冷冻产品，采用小型保冷箱等制冷措施，从而保证生鲜食材的新鲜度。且对于电动车载保冷箱或冰袋来说，配送过程中不存在开车门等影响温度而产生额外的制冷成本，因此，本文考虑不同类别的生鲜产品和需求设置不同的制冷成本。

④货损成本

由于生鲜食材易腐的特性，在配送过程中其质量会随着时间和温度的变化逐渐下降，造成货物毁损，造成一定的经济损失。对于不同种类的生鲜产品，其新鲜度衰减程度有所不同，随着时间和温度变化，冷藏冷冻产品衰减更明显；本文差异化生鲜产品的敏感度系数。同时考虑配送过程中不同的制冷方式对新鲜度的影响，引入生鲜产品保鲜努力系数。根据文献[8]构建的受时间和产品保鲜成本投入双重因素影响的新鲜度函数，构建生鲜食材种类p 到达客户i 时的新鲜度函数为：

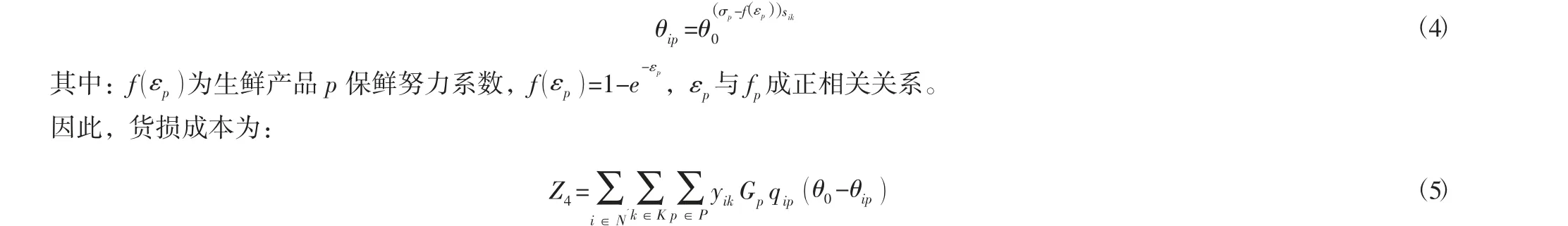
⑤时间惩罚成本

由于生鲜配送的现实情况比较复杂，车辆的行驶速度、道路复杂性等不确定因素，都有可能使货物不能在约定好的时间段内送到，本文采用配送服务软时间窗进行惩罚成本分析，即配送车辆如若超出客户指定服务时间需要承担一定的惩罚成本。

1.4.2 目标函数

综合以上成本分析，总目标函数为车辆的固定成本、运输成本、制冷成本、货损成本及时间惩罚成本之和最小。

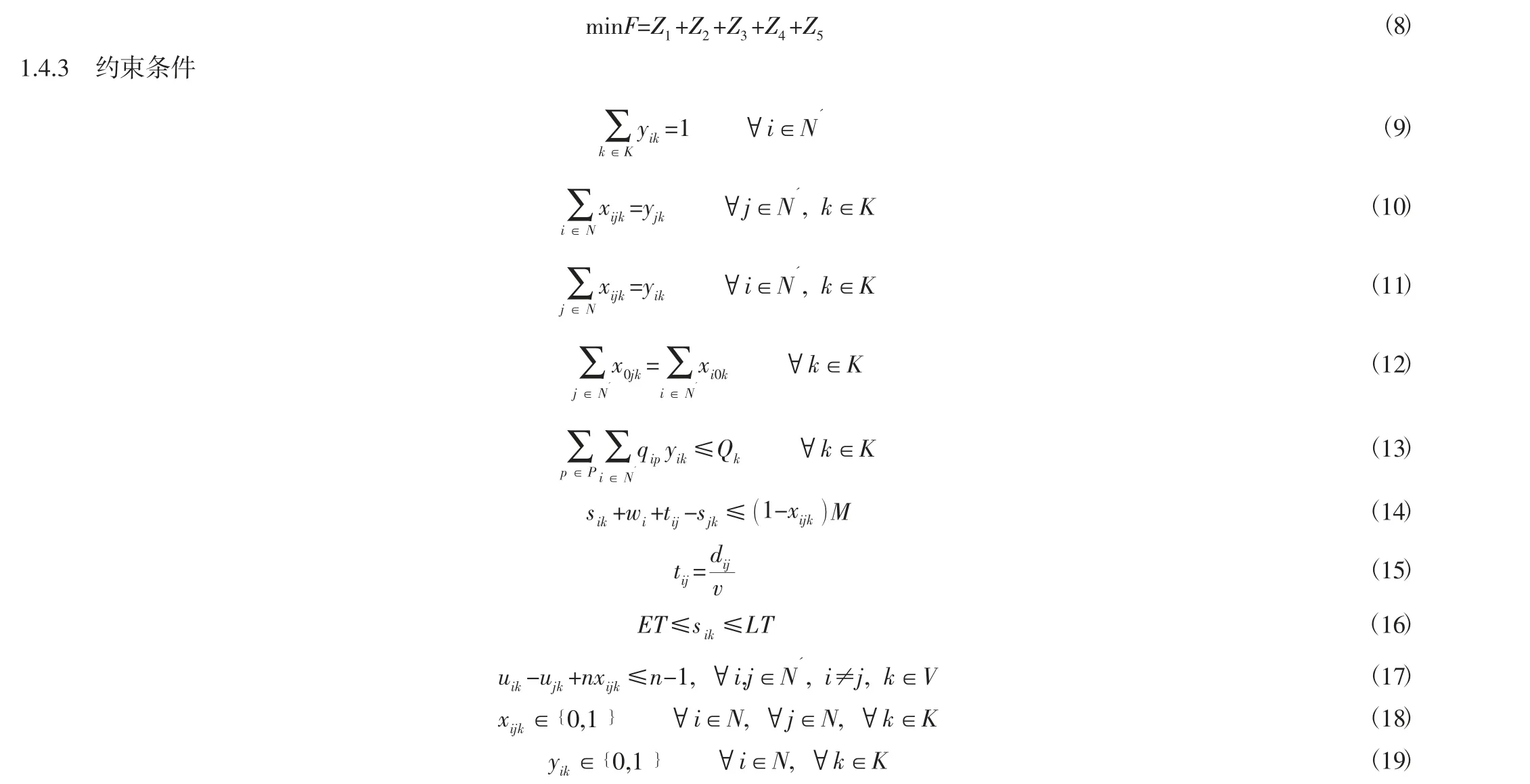
式（9） 表示每个客户都被访问一次；式（10）、式（11） 表示对于每个客户点，只允许有一辆车到达，一辆车离开；式（12） 表示电动车辆必须从生鲜配送中心出发，最终返回生鲜配送中心；式（13） 表示电动车辆容量约束，保证每辆车配送的客户点的各类生鲜需求量总和不超过电动车的最大容量；式（14） 表示电动车辆配送时间的连续性；式（15） 表示电动车辆从节点i 到节点j 的时间等于节点i 到节点j 的距离除以平均车速；式（16） 表示车辆的服务时间必须在配送中心的时间窗内；式（17） 表示消除子回路；式（18）、式（19） 表示决策变量x、y为0～1 变量。

2 混合遗传算法与设计

考虑多类型的生鲜配送路径规划属于NP 难问题，小规模算例可用精确算法求解，大规模算例的计算复杂度增加，难以在可接受时间范围内求解，因此设计混合遗传算法进行求解。

2.1 遗传算法

遗传算法（Genetic Algorithm） 是模拟自然界生物进化机制的一种算法，遵循自然界适者生存、优胜劣汰的法则，即在搜索最优解的过程中保留有用的去除无用的过程。粒子群算法（Particle Swarm Optimization，PSO） 是通过模拟鸟群觅食行为的一种基于群体协作的随机搜索算法，基本思想是利用群体中的个体对信息的共享从而使整个群体的运动在问题求解空间中产生从无序到有序的演化过程。

遗传算法具有全局搜索能力强等优点，但收敛速度慢，容易早熟。而粒子群算法收敛速度快，但容易陷入局部最优。因此，本文将两种算法混合使用，从而更快的获得更优的解。算法流程图如图1 所示。

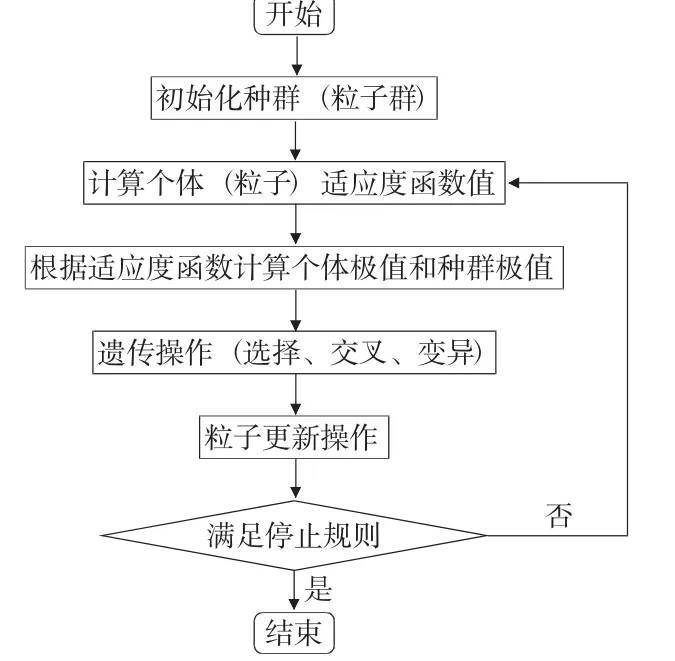
图1 算法流程图

2.2 算法设计

2.2.1 染色体编码

财务人员管理是加强财务管理的基础，财务人员是具体监管政策的执行者。政府监管部门及民办非营利性医疗机构应重视加强对财务人员的业务培训,促进他们提高业务能力和工作水平。主管部门在财务人员业务培训时，应要求公立医疗机构和民办医疗机构统一接受培训。

本文采用整数编码。根据客户数目n，对客户进行排序，生成长度为n 的染色体。根据车辆的容量约束进行解码，根据车辆容量按顺序将客户分配到每一辆车，如车辆容量可以满足一条染色体上客户i 到j 的需求，则从客户j+1 起的路径，由配送中心的另一辆车配送，直到染色体上的客户都被访问，由此生成不同的配送路径。

2.2.2 种群初始化及适应度函数

初始种群采用随机生成，来保证个体的多样性。适应度是衡量染色体个体优劣的标准，也是进行选择算子操作的重要依据，适应度低的染色体个体会通过选择算子进行淘汰。本文的生鲜产品配送路线优化模型的优化目标是希望综合成本越小，对应的适应度就越大，得到的解就越优。因此可选择综合成本倒数作为适应度函数。即：

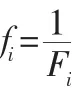
其中：f是染色体i 的适应度值，F是染色体i 所对应的的目标函数值。

2.2.3 选择操作

2.2.4 交叉操作

采用单点交叉。随机选取两个染色体作为父本，在父代染色体中只随机设置一个交叉点，将染色体分成两部分，把两个父本个体的部分基因片段进行交换，删除重复基因，补充缺少的基因，从而得到两个新个体。单点交叉过程如图2 所示。

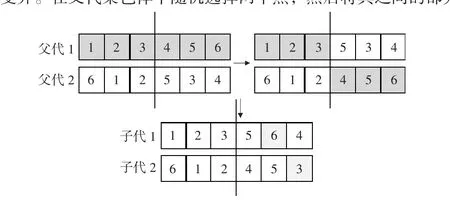
图2 单点交叉

采用逆转变异。在父代染色体中随机选择两个点，然后将其之间的部分进行反转。逆转变异如图3 所示。

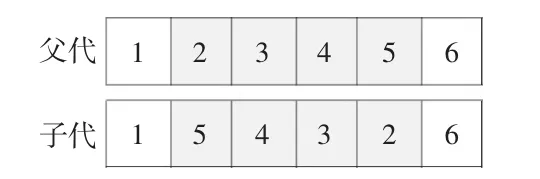
图3 逆转变异

2.2.6 粒子更新操作

离散PSO 算法对粒子更新的运算符进行了重新定义，文献[9]给出了运算符说明，粒子的速度和位置的更新公式为：别为自我学习因子和群体学习因子，p是粒子自身目前经历的最优位置，g是整个粒子群目前经历的最优位置。运算符! 作用后，当前粒子调整为最优位置的序列；运算符⊗与ω、c、c作用后，按概率保留速度中的调整序列，得到新速度；运算符⊕为调整序列的叠加作用。

3 算例分析

3.1 数据选取

数据选自Solomon 标准算例数据库中R 类型（随机分布）中的R101 算例，算例选取25 个客户，1 个生鲜配送中心，生鲜配送中心及客户位置如图4 所示。对客户各个种类的生鲜需求量等参数进行合理调整。其他参数设置如表2 所示。

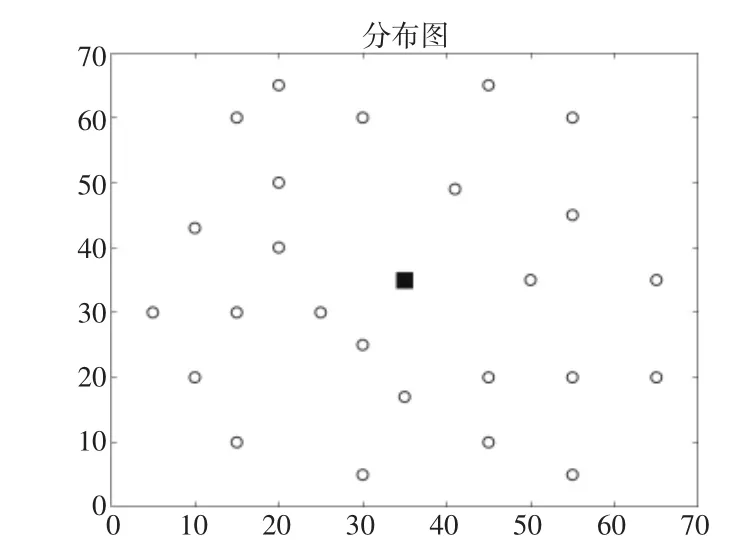
图4 R101 算例节点位置分布

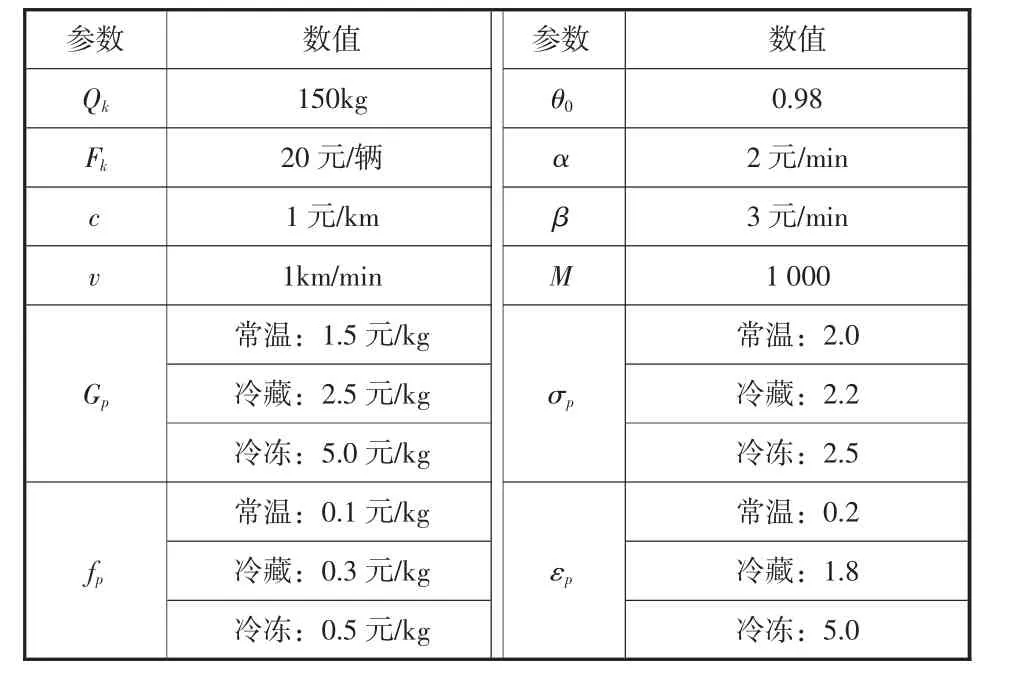
表2 本文参数设置

3.2 结果分析

在Windows10 操作系统下，RAM 为8G，Intel（R） Core（TM） i5-8265U 的处理器上应用Matlab R2017b 编写算法进行模型求解。

设定种群大小为200，终止进化代数为500，交叉概率为0.9，变异概率为0.05，惯性权重最大值为0.96，惯性权重最小值为0.4，自我学习因子为0.5，群体学习因子为0.5。分别用传统遗传算法和混合遗传粒子群算法重复求解10 次，记录每次运行的解及时间，并给出每次的解与10 次运行中最优解的偏差值（GAP），如表3 所示。

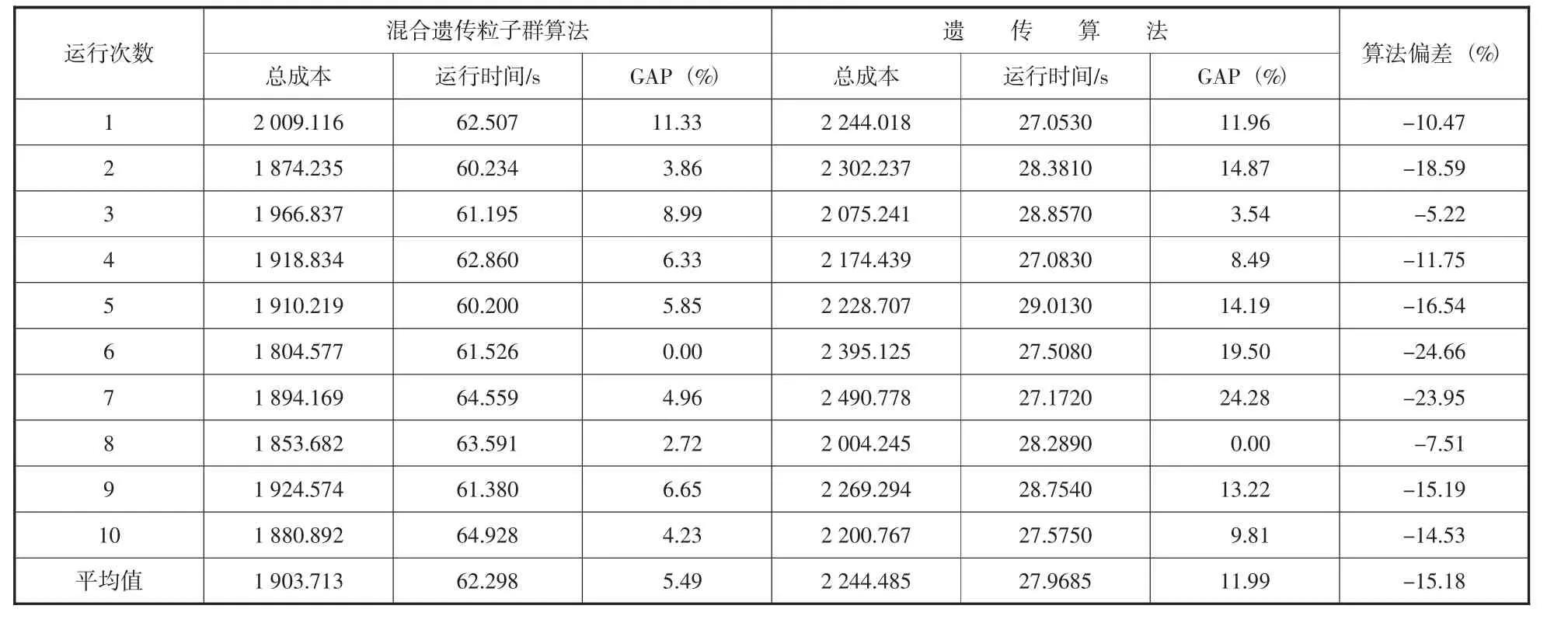
表3 模型求解10 次运行结果

R101 算例用遗传算法求解10 次的平均运行时间为27.9685 秒，最优解为2 004.245，平均解为2 244.485，解的平均偏差值为11.99%，最大偏差值为24.28%；用混合遗传粒子群算法求解10 次的平均运行时间为62.298 秒，最优解为1 804.577，平均解为1 903.713，解的平均偏差值为5.49%，最大偏差值为11.33%。与传统遗传算法相比，混合遗传粒子群算法在解的质量上得到明显改善，目标值平均降低15.18%；此外混合遗传粒子群算法的平均偏差值也要比遗传算法小，说明其算法稳定性较好。运行时间方面，混合遗传算法加入了粒子更新寻优操作，运行时间较遗传算法略有增加，但仍然在可接受范围内。

取10 次运行解最小的结果作为最优路线，得到如下结果。遗传算法和混合遗传粒子群算法迭代次数如图5 所示；图6 为遗传算法和混合遗传粒子群算法求解的最优配送路径图。

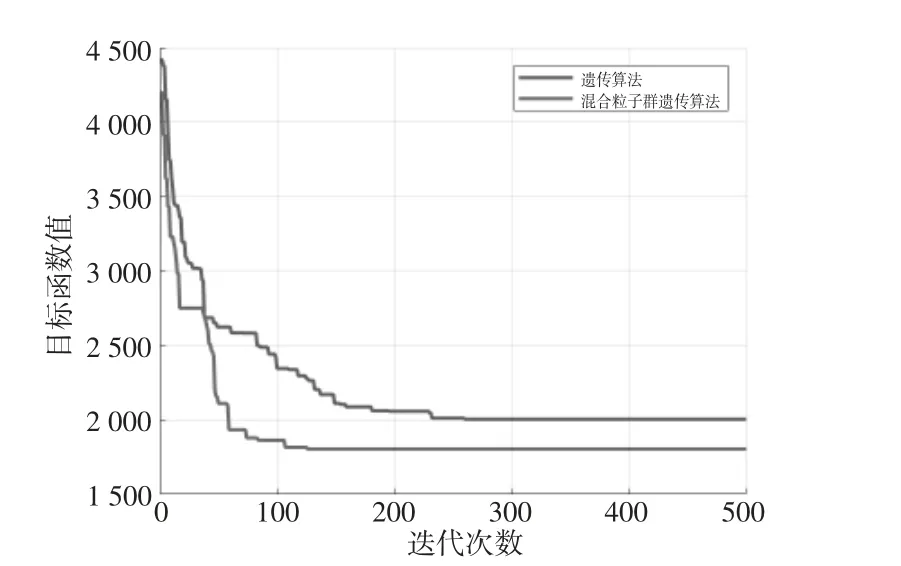
图5 算法迭代收敛示意图

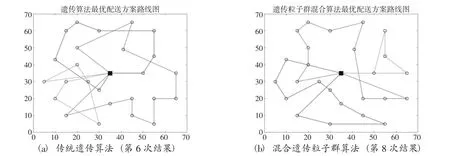
图6 最优配送路径图

与遗传算法相比，混合遗传粒子群算法的收敛速度更快，求得的解更优，说明本文设计的混合遗传粒子群算法求解性能较好。表4 给出了两种算法10 次求解的最优解结果。

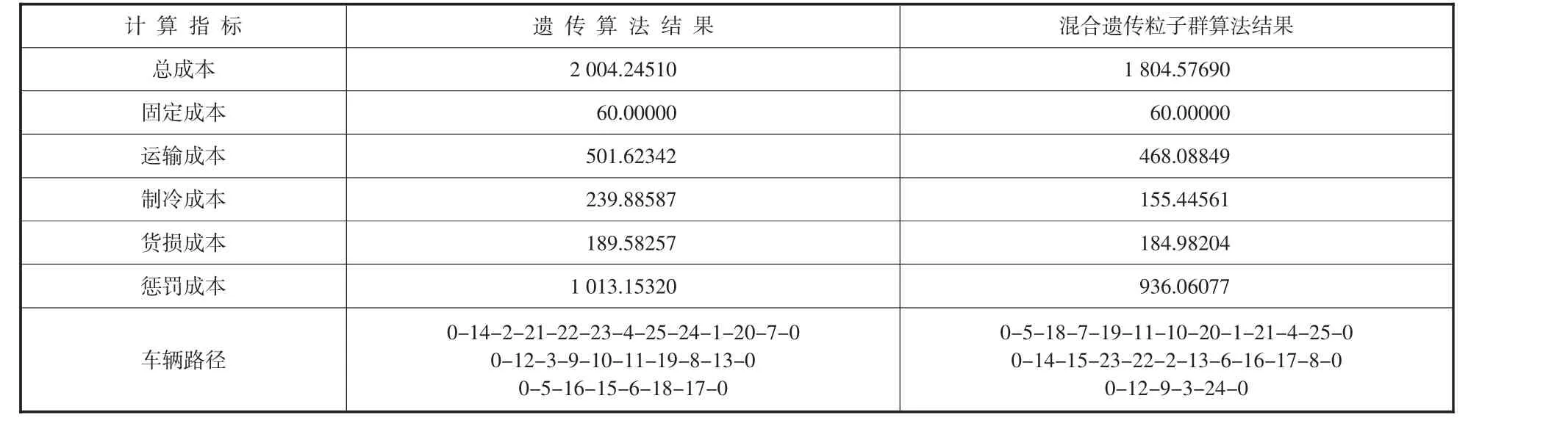
表4 算法结果对比

3.3 灵敏度分析

企业在生鲜配送末端采取不同的保鲜措施，会影响配送成本及货物损失成本。为了进一步研究不同的生鲜保鲜投入对企业成本及产品货损的影响，以便在生鲜配送过程中采取合理的保险措施，分别设置不同的生鲜产品单位制冷成本，对应不同的生鲜保鲜投入系数，每次实验运行10 次取平均值，对比分析各项成本，如表5 所示。

表5 单位制冷成本及生鲜保鲜投入系数灵敏度分析

从表5 中可以得出，随着生鲜保鲜投入的升高，制冷成本与货损成本的变化呈悖反关系。但综合这两项成本之和及总成本的变化并非单调，如图7 所示。这是由于随着生鲜保鲜投入的变化，制冷成本和货损成本变化的幅度不同，制冷成本增速变快，货损成本下降的趋势变缓，因此，当为降低货损成本，对三种生鲜产品都采取制冷箱等保鲜投入较高的措施是不值得的。三种不同设置中，设置2（三类产品都采用冷藏措施） 的两项成本之和及总成本最低，但相比这三种设置均对不同的产品采用一种保鲜措施，本文设置求得了最低的总成本，因此需要合理的设置对于不同种类生鲜的保鲜措施，以此来平衡制冷成本和货损成本，从而使得系统最优。

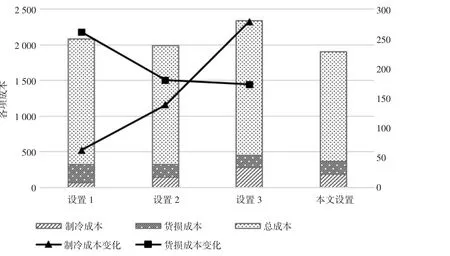
图7 不同生鲜投入系数对比分析

4 结 论

针对生鲜配送路径优化问题，本文构建了以固定成本、运输成本、制冷成本、货损成本及时间惩罚成本总成本最小化为目标的路径优化模型。与传统配送问题相比，由于不同种类的生鲜产品随时间的损耗不同，且时间要求较高，本文考虑不同种类的生鲜产品采用不同的保鲜方式，差异化新鲜敏感度敏感系数，引入生鲜保鲜努力系数，构建生鲜配送路径优化模型；通过设计混合遗传粒子群算法，利用Matlab 进行了算例验证，通过对比分析传统遗传算法和混合遗传粒子群算法，结果表明，混合遗传粒子群算法在求解本文模型方面，求得的解更优，稳定性更好。针对生鲜配送过程中保鲜措施的选择，进行了生鲜保鲜投入系数灵敏度分析，结果表明，随着生鲜保鲜投入的升高，制冷成本与货损成本的变化呈悖反关系，但对于综合成本的影响，系统最优的保鲜策略是不同的生鲜产品采取不同的制冷措施，以此来平衡各项成本。

生鲜配送活动中存在许多不确定性，本文建立的模型中忽略了许多影响因素，研究可以进一步扩展，考虑生鲜需求波动等因素对于配送成本的影响。