跨线钢箱梁斜拉桥列车风荷载及风致振动

周小刚，张 迅，陈 韬，邱敏捷，罗 实

(1.西南交通大学桥梁工程系，成都 610031；2.中铁二院成都勘察设计研究院有限责任公司，成都 610031)

列车运行时带动车体表面空气一起运动并压缩周围空气，造成空气非定常湍流流动。这种空气湍流流动也被称为“列车风”或“气动力”。近年来，随着列车车速不断提高，列车风诱发的工程问题日益突出，主要涉及行车安全、旅客舒适度和邻近结构异常振动等[1]。

针对列车气动力的研究，目前以模型试验、实车测量、数值模拟等3种方法为主[2-3]。Gerhardt等[4]以德国3座火车站为背景，研究了列车高速过站对周围结构产生的风荷载，并提出了可行的抑振措施；何佳骏，何旭辉等[5-8]对高速列车通过全封闭式、半封闭式及直立式声屏障的气动压力波开展了研究；宋杰[9]将现场实测与数值模拟结合，对列车过站时的风压分布及站台雨棚和天桥的振动响应进行了分析；陈玥[10]研究了车、桥之间的距离及行车速度对气动力的影响，并分析了跨线混凝土斜拉桥的动力响应；蒋丽等[11]考察了列车风作用下车站人行天桥的动力响应和舒适度；米宏广[12]以某张弦梁雨棚为背景，分析了列车高速通过时雨棚表面的风压分布及雨棚动力响应；张帅[13]考察了跨线天桥及雨棚在列车风作用下的脉动特性和不同参数下的动力响应变化规律；YANG N等[14]研究了高速列车下穿跨线天桥时不同梁宽及梁高对梁体表面风压的影响；余洋[15]对杭州南站幕墙受过站列车的风荷载进行了定量评估。

当前，伴随着我国铁路网的不断扩张，公路及城市道路桥梁的跨线情况逐渐增多[16]，如图1所示的跨线桥梁工程。该桥为独塔无背索斜拉桥，桥跨布置为(40+188+55)m，主跨采用扁平钢箱梁，施工方法为转体施工。

图1 (40+188+55)m独塔无背索钢箱梁斜拉桥(单位：m)

相比混凝土主梁而言[17]，钢箱梁表面积大、自重轻、结构刚度低、阻尼小，故高速列车下穿时的气动力可能引起较大的桥梁振动响应。然而，当前国内外针对此类问题的研究非常有限。为此，采用流体分析软件FLUENT进行CFD仿真，并采用有限元软件Midas/Civil进行桥梁动力分析。关注点是高速列车下穿时的列车风和桥梁振动响应特性，研究方法和主要结论可为相关工程技术人员提供参考。

1 CFD仿真与验证

1.1 基本理论

标准k～ε双方程模型由于具有高效、准确、适应性广等特点，成为目前应用最广泛的湍流模型之一[18]。与湍流动能k、湍流耗散率ε相对应的运动方程可表示为

Gb-ρε

(1)

(2)

式中，Gb，G3ε均与浮力相关，在本研究中可忽略；ρ为空气密度，取1.225 kg/m3；C1ε，C2ε，σk，σε为常量，分别取1.44、1.92，1.0，1.3。

湍流动能增项Gk、黏性系数μt计算式为

(3)

(4)

式中，Cμ为常量，取0.09。

1.2 主要建模技术

(1)模型简化

考虑到建模工作量，忽略受电弓、列车门、转向架等局部细节，但保留列车主要气动外形。据文献[19]的研究成果，在分析列车气动力时，3节车编组与8节、16节车编组的计算结果相似。因此，采取3节车进行列车风模拟(图2)，并将风压时程延拓后得到8节车对应的风压时程。考虑到列车风压的影响范围，仅取一定长度的梁体进行建模。经过反复试算，最终选用的尺寸如图3所示。

图2 3节车体模型(单位：m)

图3 钢箱梁模型(单位：m)

(2)动态铺层技术

使用动态铺层技术模拟列车与桥梁的相对运动时，可将网格划分为动网格与静网格区域。在列车运动过程中，网格合并及分裂只发生在动网格区域，而外部静网格区域不发生网格重构，故可大幅减少计算量。

网格划分时，首先对动网格和静网格区域分别进行划分，再进行网格合并。内部动网格及外部静网格区域如图4所示。针对流场变化剧烈、重点关心区域(如车体、梁体周围等)，进行网格加密处理。最后，为避免外流场边界对计算结果的影响，计算区域取为367.5 m×168.1 m×78.2 m，列车初始位置距桥梁38 m。

图4 计算分析域(单位：m)

通过Interface交界面实现动网格与静网格区域的数据交换，动网格区域如图5所示。

图5 动网格区域(单位：m)

网格是否发生合并及分裂由预定义的合并高度hc及分裂高度hs决定，其计算式如下

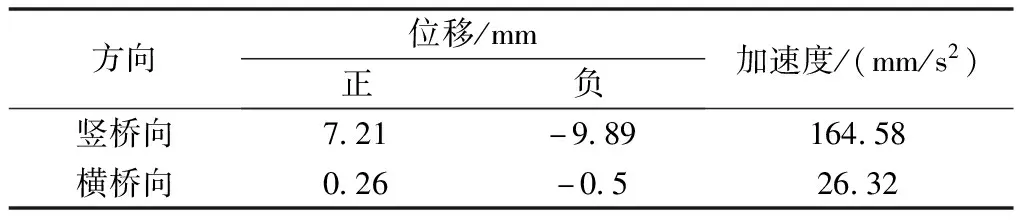
hc

(5)

hs>(1+as)h0

(6)

式中，坍塌因子ac取0.2；分裂因子as取0.4；h0取0.5 m。

1.3 仿真验证

为验证CFD仿真结果的可靠性，以文献[20]中人行天桥为对象，使用与本文相同的计算方法和参数设置对气动力进行模拟。图6为人行天桥的尺寸及风压监测点，梁底距轨顶高度为8 m。图7给出了列车以速度250 km/h运行时，梁体表面监测点的风压实测值和仿真值。

图6 列车下穿人行天桥(单位：m)

图7 风压仿真值与实测值对比

通过图7中的对比可得到如下结论。

(1)从风压时变特性来看，数值模拟的列车风压时程与实测列车风压时程基本一致。当头车接近监测点时，气动正压力迅速上升至正极值，随后快速转为气动负压力至负极值，其通常称为“头波”。当车体中部通过监测点时，气动压力在一极小值附近波动。当尾车接近监测点时，气动负压力迅速下降至负极值，随后快速上升到气动正压力至正极值，其通常称为“尾波”。

(2)从压力数值来看，仿真“头波”正压极值小于实测值10 Pa，仿真负压极值大于实测值13 Pa；仿真“尾波”正压极值大于实测值3 Pa，仿真负压极值大于实测值10 Pa。总体上，上述仿真误差较小，均处于工程上可接受的范围内。因此，基于FLUENT的数值仿真能够较为准确地模拟高速列车下穿跨线桥时的气动风压。

2 列车风特性

采用前节所描述的分析方法和参数设置，对图1所示跨线桥进行仿真。

计算条件如下：车、桥相交角度为90°；车速取为350 km/h；轨顶到梁底高度设为建筑限界7.25 m。需要指出的是，本桥与既有铁路的实际相交角度为66°，梁底距轨面的高度约为12 m，目前铁路运营时速为120～140 km。前述计算条件为高于实际情况的偏保守考虑。

钢箱梁顶板受列车风的影响小，本节不再进行讨论。选取轨道中心线上方顺桥向2 m长范围内的梁体进行考察，并将其划分为若干小块，见图8。图9给出了钢箱梁翼缘板、腹板及底板各分块的平均风压时程曲线。

图8 钢箱梁各分块示意(单位：m)

图9 钢箱梁各分块风压时程曲线

图10 不同车-桥间距下的风压极值

最后，对距轨道中心线不同距离的钢箱梁断面进行风压监测，结果如图11所示。

图11 钢箱梁不同断面的风压极值

结合图8～图11可知。

(1)翼缘板、腹板及底板各分块的风压变化规律相同，均表现出明显的“头波”及“尾波”效应。

(2)翼缘板附近流动变化剧烈，相邻分块的风压极值表现出较大的差异性，这主要是受到桥上声屏障和腹板的影响。

(3)对于腹板，气动压力幅值随着距离轨面高度的增大而减小。在“头波”段，迎风面正压幅值略高于背风面正压幅值，负压幅值略低于背风面负压幅值，而在“尾波”段，大小关系正好相反。

(4)对于底板，各分块的压力幅值变化均不大，这主要是由于其距离轨面的高度一致。

(5)随着车-桥间距的增加(从5.25 m变化到9.25 m)，风压极值不断衰减，正、负压极值衰减规律相似，且底板和腹板处的衰减速率较翼缘板处更快。随着距轨道中心线距离的增加，不同断面钢箱梁的风压极值衰减规律与前述衰减规律相似。

但是，气息的运用也不是孤立地，是要与指下的功夫相辅相成的。我们在弹奏琴曲的时候不仅仅只是靠气息或是指下的技术来完成乐曲，例如：弹奏《仙翁操》的时候，要在气息与指法上达到和谐，在实音与泛音之间去领会这种虚实结合带来的空间立体感，从而聆听出弦外之意。

3 风致振动响应

基于Midas/Civil软件建立桥梁动力分析模型。其中，斜拉索采用杆单元模拟，塔、梁、墩均采用梁单元模拟。转体阶段和运营阶段的计算模型分别见图12、图13。

图12 转体阶段有限元模型

图13 运营阶段有限元模型

3.1 加载方法

在累加计算梁体受到的气动力时，对梁体以2.5 m长为一节段进行划分，见图14。

图14 梁体节段划分示意(单位：m)

通过分析梁体L1～L8，R1～R8节段的三分力变化规律(图15、图16)，可得出如下结论：作用于梁体上的气动力沿轨道中心线左右对称分布。在距中心线20 m处，三分力极值分别下降为轨道中心线处的28%，23%和11%，见表1。

表1 三分力极值变化

图15 L1～L8节段的升力、阻力和扭矩时程曲线

图16 沿梁体纵向的升力、阻力和扭矩极值

3.2 施工阶段的风致振动

本桥转体施工计划在天窗时间进行。转体完成后，主跨支撑在临时墩上，合龙口位置见图1。

首先，对梁体处于悬臂未合龙状态进行分析。表2给出了前3阶模态及自振频率。

表2 转体阶段自振频率

考虑到对梁体的最不利影响，选择靠近梁端一侧的股道进行气动力加载，如图17所示。

气动力加载持续时间为尾车通过后梁体表面风压降至0 Pa附近，约为3.24 s。计算时间步为0.04 s。取典型监测点(图17中的点1、点2、点3、点4、点5)的竖桥向位移、横桥向位移、竖桥向加速度、横桥向加速度分别进行讨论，计算结果如图18～图20所示。表3列出了梁端位移及加速度的最大值。

图17 气动力加载及监测点示意(单位：m)

图18 典型监测点的位移时程曲线

图19 典型监测点的加速度时程曲线

图20 梁体位移极值包络图

表3 梁端位移及加速度最大值

通过分析图18～图20及表3可知：最大位移和加速度均出现在梁端，对应图17中的监测点1。最大竖桥向位移为9.89 mm，最大横桥向位移为0.50 mm，最大竖桥向加速度为164.58 mm/s2，最大横桥向加速度为26.32 mm/s2。结合施工控制精度可知，列车风对钢箱梁合龙施工的影响有限。

3.3 运营阶段的风致振动

采用与上节相同的方法考察运营阶段跨中附近股道出现列车下穿时的桥梁动力响应。此时，最大位移及加速度均出现在跨中附近，计算结果见表4。

表4 跨中梁体位移及加速度最大值

从表4可以看出：相比施工阶段而言，运营阶段梁体位移和加速度更小，这主要是因为全桥边界约束更强、整体刚度更大。在运营阶段，最大竖桥向位移为3.24 mm，最大横桥向位移为0.16 mm，最大竖桥向加速度为91.95 mm/s2，最大横桥向加速度为32.17 mm/s2。

4 结论

(1)高速列车下穿时，钢箱梁翼缘板、腹板及底板的表面风压均表现出明显的“头波”“尾波”特性。邻近部分的扰动和距离轨面的高度共同影响不同区域的风压分布规律。

(2)随着车-桥间距和距轨道中心线距离的增加，风压极值不断衰减，底板、腹板处的衰减速率较翼缘板处更快。

(3)对于梁段气动力而言，各节段升力、阻力及扭矩变化规律相同，其数值沿顺桥向快速下降。在距轨道中心线20 m处，各分力极值分别下降为轨道中心线处的28%、23%和11%。

(4)对于桥梁振动响应而言，施工阶段的最不利位置出现在梁端。其中，最大竖桥向位移为9.89 mm，最大竖桥向加速度为164.58 mm/s2。在运营阶段，跨中的最大竖桥向位移为3.24 mm，最大竖桥向加速度为91.95 mm/s2。

从研究结果来看，列车风对钢箱梁合龙施工的影响有限(竖桥向振动小于1 cm)，但仍应加强监测，以避免临时墩受力较大对钢箱梁不利。在运营阶段，由于整体刚度更大，列车风的影响可忽略。