高速铁路桥墩沉降与无砟轨道底座板脱空区域的映射关系
陈天浩,杨建伟,王金海
(1.北京建筑大学机电与车辆工程学院,北京 100044;2.北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室,北京 100044)
桥梁结构在高速铁路中占很大比例,其主要功能是为高速列车提供平滑稳定的线路,以确保运行和乘坐舒适性[1-3]。在桥梁的建造和运营中,由于一些有害因素,例如不合理的设计,超负荷运行和极端天气,不可避免地会导致桥墩沉降。不均匀的沉降将导致桥梁下沉,并且轨道表面发生变形。此外,轨道底座板和桥面板之间还有一些脱空区域。当列车高速通过时,底座板与桥面板的脱空区域会加剧轨道系统的损坏并缩短使用寿命[4-6]。桥墩沉降引起的钢轨变形会对轮轨接触产生干扰,恶化列车的安全性和稳定性,甚至导致列车脱轨[7,8]。为了保证轨道系统的可靠性和高速列车的舒适性[9],有必要研究桥墩沉降与轨道系统之间的映射关系。映射关系在桥梁轨道系统的维护和运营中起着至关重要的作用。
一些研究人员在铁路与桥梁或铁路与路基之间的映射关系方面开展了卓有成效的研究工作,可分为解析法和有限元法。在解析法中,陈兆伟等[11-12]推导了不同轨道系统下桥墩沉降与钢轨竖向变形之间的映射表达式,发现在纵向连接的无砟轨道系统中,桥墩沉降将导致底座板和梁部分分离。一些研究人员研究了桥墩沉降对不同轨道系统(如CRTSⅠ,Ⅱ和Ⅲ)的影响,并获得了沉降极限值[13-15]。一些研究人员研究了沉降条件下扣件刚度[15-16]和砂浆层刚度[16]对轨道位移曲线的影响。陈兆伟等[17-19]比较了单墩沉降模型(SPSM)和多墩沉降模型(MPSM),发现SPSM和MPSM具有相似之处。从MPSM获得的结果是SPSM计算结果的叠加。此外,姜力等[20-21]计算了桥梁结构3种典型变形下的钢轨变形,分析了钢轨几何形状的演变,并得出桥梁结构变形与钢轨变形的映射系数随着桥梁结构变形幅度的增加呈非线性增加的结论。郭宇等[22-23]研究了不同路基沉降值下轨道与路基的接触关系,通过半解析法推导了路基沉降与轨道之间的映射关系。何春艳等[24]研究了列车在路基-桥梁过渡段中的动力特性,推导了钢轨变形与路基不均匀沉降之间的映射关系。
在有限元方法中,研究人员通过建模验证了上述映射关系的正确性和准确性,然后研究了车辆在沉降条件下的动态响应。苟洪业等[25]通过建立车辆-轨道-桥梁模型来分析不同桥梁变形条件下车辆的动态响应。结果表明,竖向桥梁变形主要影响竖向车辆动力指标,而对横向动力指标的影响可忽略不计。郑岚等[26]分析了桥墩沉降和梁断裂对不同类型高速列车乘坐舒适性的影响。根据仿真结果,不同列车的动态响应显示出明显不同的灵敏度。张晓慧[27]比较了不同跨度桥梁下车辆的动力响应,发现跨度为24 m的梁所有动力响应比跨度为32 m的动力响应略大。
尽管目前取得了上述进展,但大多数学者均是使用有限元模型进行模拟,或者是推导钢轨变形与桥墩沉降之间的映射关系。很少有文献使用解析法来研究桥墩沉降与轨道底座板脱空区域之间的映射关系。本文推导了纵向连接板式无砟轨道条件下桥墩沉降与轨道底座板脱空区域映射关系的解析表达式,并用有限元模型进行了模拟验证,还分析了桥梁表面刚度对脱空区域的影响。
1 轨道底座板脱空的机理分析
简支梁桥发生沉降时,沉降处相邻的跨梁由于重力发生垂向位移,轨道结构也随之变形。图1所示为纵连板式无砟轨道轨道底座板与桥面板间脱空区域的示意。

图1 纵连板式轨道结构底座板随桥墩沉降脱空区域示意
轨道底座板连同整个轨道系统结构在重力作用下发生垂向位移,因为轨道的纵向联结特性,底座板与桥面板在A,B,C处产生分离。P位置处的底座板与桥面板接触成因是桥墩沉降导致桥梁转动抬起所致。而Q位置的接触则是由于轨道系统的垂向位移与梁体位移相等所致。因此,沉降值的大小直接影响脱空区域的范围以及底座板与桥面板间的间距大小。
2 脱空区域的求解
2.1 脱空区域求解表达式
在对轨道-桥梁系统分析前,将钢轨、轨道板和底座板考虑为自由梁,并作如下假设:
(1)考虑变形过程中钢轨对轨道板、轨道板对底座板的影响,不考虑底座板对桥梁板的影响;
(2)不考虑砂浆层的离缝,并且将砂浆层等效为线性弹簧;
(3)桥梁与底座板之间等效为单向受压弹簧接触。
本文对轨道-桥梁系统进行分析时,桥梁取为4跨,每跨桥长度为32.6 m,有N个扣件。
2.1.1 钢轨变形的解析表达式
沿钢轨方向设为x方向,按0.01 m将钢轨分成M个单元,每个单元的重力表示为Gr=mrglR,mr为钢轨单位长度质量,g为重力加速度,lR为钢轨单元的长度,即0.01 m。Fr为扣件弹簧力,本文中扣件间距lf设为0.6 m,如图2所示。

图2 钢轨受力分析图式
钢轨视为自由梁,受到重力和扣件弹簧力的作用。钢轨的两端可以视为两端点扣件的弹簧支撑,分别为F(r,1)和F(r,4N)。因此,自由梁的弹性变形可以按简支梁弯曲变形模型来求解,如图3所示。
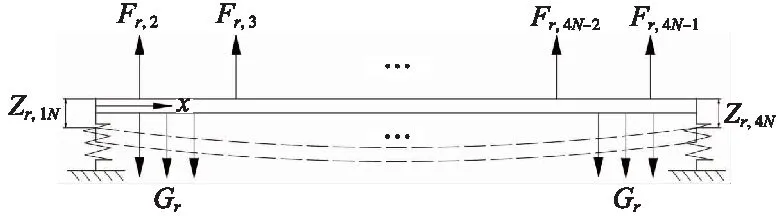
图3 自由梁模型分解
自由梁两端点的垂向刚性位移为
(1)
其中,kp为扣件弹簧刚度。
钢轨两端点以外,钢轨各位置的位移表达式为
(2)
式中Er——钢轨弹性模量;
Ir——钢轨截面惯量;
lr——钢轨长度;
Xr,j——第j个钢轨单元距离钢轨左端的距离。
结合式(1)和式(2),钢轨各单元的位移矩阵为
Zr=A·Gr-B·Fr
(3)
式中,Zr为所有钢轨单元的位移矩阵;A和B分别为重力Gr和扣件力Fr对钢轨变形的作用效果矩阵。其中
(4)
(5)
(6)
(7)
因为扣件间距lf为0.6 m,因此扣件力Fr只有在x=0.6,1.2 m…的位置才会对钢轨变形产生作用效果。
2.1.2 轨道板变形的解析表达式
轨道板在重力、扣件弹簧力Fr和砂浆的支承力的作用下发生弹性变形,受力分析如图4所示。如同上文中钢轨分析一样,将轨道板沿x方向,按0.01 m分成M个单元,每个单元的重力用Gs表示。将砂浆层的作用力等效为弹簧力Fs,弹簧间距为0.01 m。

图4 轨道板受力分析图式
同上,轨道板两端点的垂向刚性位移为
(8)
其中,ks为砂浆等效弹簧刚度。
轨道板除去两端点以外的位移表达式为
(9)
式中Es——轨道板弹性模量;
Is——轨道板截面惯量;
ls——轨道板长度;
Xs,j——第j个轨道板单元距离轨道板左端的距离。
结合式(8)和式(9),轨道板各单元的位移矩阵为
Zs=C1·Gs-C2·Fr-D·Fs
(10)
式中,Zs为所有轨道板单元的位移矩阵;C1、C2和D分别为重力Gs、扣件力Fr和砂浆等效弹簧力Fs对轨道板变形的作用效果矩阵。其表达形式与上文中力对钢轨变形的作用效果矩阵类似,因此不再列出。
2.1.3 底座板变形的解析表达式
底座板在重力、砂浆作用力Fs和接触力Fp的作用下发生弹性变形,受力分析如图5所示。如同上文,将底座板沿x方向,按0.01 m分成M个单元,每个单元的重力用Gp表示。接触力Fp的弹簧刚度设为kb,间距设为0.01 m。

图5 底座板受力分析图式
底座板两端点的垂向刚性位移为
(11)
其中,kb为桥梁板接触刚度。
底座板除去两端点以外的位移表达式为
(12)
其中Ep——底座板的弹性模量;
Ip——底座板截面惯量;
lp——底座板长度;
Xp,j——第j个底座板单元距离底座板左端的距离。
结合式(11)和式(12),底座板各单元的位移矩阵为
Zp=G(Gp+Fs)-H·Fp
(13)
式中,Zp为所有底座板单元的位移矩阵;G和H分别为重力Gp、砂浆等效弹簧力Fs和接触力Fp对轨道板变形的作用效果矩阵。
2.1.4 桥梁沉降位移
如图6所示,3号桥墩发生沉降d,第2和第3跨梁发生垂向位移。第1跨和第4跨梁的垂向位移为0。

图6 桥墩沉降示意
图7为第2跨梁体位移,lb1为梁端到支座的距离,lb0为梁支座之间的距离。

图7 第2跨梁体位移示意
沿桥梁的纵向,0.01 m为一个单元长度,则对应每个单元处的桥梁位移为
Zb,i=(xb,i-lb1)×d/lb0
(14)
式中,x(b,i)为第2跨梁上第i个单元距左端的距离。
同理求得第3跨梁各单元处的位移,最后得出四跨桥梁的垂向位移矩阵Zb。
2.1.5 扣件弹簧力
第i个扣件弹簧力为
Fr,i=kp(Zr,i-Zs,i)
(15)
因此,扣件弹簧力矩阵可表示为
Fr=kp(Zr-Zs)
(16)
2.1.6 砂浆等效弹簧力
第i个砂浆等效弹簧力为
Fs,i=ks(Zs,i-Zp,i)
(17)
因此,砂浆等效弹簧力矩阵可表示为
Fs=ks(Zs-Zp)
(18)
2.1.7 接触力
第i个接触力为
Fp,i=kb,i(Zp,i-Zb,i)
(19)
(20)
因此,接触力矩阵可表示为
Fp=Kb·(Zp-Zb)
(21)
式中,Kb为接触力刚度矩阵。
2.1.8 脱空区域的求解
联立式(3),式(10),式(13),式(16),式(18)和式(21)可得
(22)
式中,E为单位矩阵。
底座板和桥梁板的脱空区域范围通过如下步骤循环迭代求解:
(1)假设底座板和桥梁板初始是全接触,则对于i=1~M,都有kb,i=kb;
(2)通过式(22)可以求出Zp,i和Zb,i。通过判断Zp,i和Zb,i的大小,如果Zp,i>Zb,i,则i点对应的位置为接触状态,反之则为脱空区域,并令Ki,i=0;
(3)循环步骤2,直到接触力刚度矩阵Kb稳定,即可得到Kb矩阵。并且通过底座板位移矩阵Zp和桥梁板位移矩阵Zb对比得出脱空区域的范围。
2.2 脱空区域解析的有限元验证
在ABAQUS中建立轨道-桥梁系统有限元模型,得到该系统随桥墩沉降而产生的脱空区域范围的数值解,以此来验证脱空区域范围的解析表达式。考虑到模型的结构对称性,取4跨轨道-桥梁系统,沉降发生在最中间处,进行建模分析。模型如图8所示。

图8 轨道-桥梁有限元模型
在该模型中,桥梁板和底座板、底座板和砂浆层、砂浆层和轨道板之间采用表面-表面的接触方式,轨道板和钢轨之间的接触关系用TIE约束的方式,各部件弹性模量参数如表1所示。

表1 有限元模型中各部件的弹性模量参数 Pa
计算时,桥梁长度取4×32.6 m,沉降量取30 mm,将有限元模型得出的底座板位移大小对解析表达式得到的结果进行验证,验证结果如图9所示。

图9 底座板位移
由于底座板的纵向联结特性,随着中部桥墩沉降的产生,底座板随之产生垂向变形,在进入沉降区域时,底座板会稍微上翘,这是由于中部沉降导致梁体转动,两端因此被抬起。在沉降区域,底座板位移达到最大值,且有缓和过渡曲线。由有限元模型和解析模型得出的底座板位移基本吻合,说明解析模型完全可以用于求解纵连板式轨道系统下桥墩沉降引起的底座板脱空区域。相比于有限元模型,解析模型更容易表现出轨道系统各参数之间的关系,而且建模更加方便,下文将采用解析模型来分析底座板脱空区域。
3 不同沉降量引起的脱空区域分析
每跨桥梁长度为32.6 m,沉降量d分别取5,10,15,20,25,30 mm和35 mm,底座板与桥梁板间的间隙如图10所示。

图10 不同沉降量下底座板到桥梁板的间距
由图10可知,桥墩沉降引起的底座板脱空区域一共有5处,分别位于3号桥墩(x=65.2 m)处,以及2号(x=32.6 m)和4号桥墩(x=97.8 m)相邻的左右位置,脱空区域的大小呈对称状,故取2号桥墩左右位置和3号桥墩处的脱空区域范围进行详细阐述,如图11和图12所示。

图11 第2个桥墩左右位置处底座板到桥梁板间距
由图11可得,脱空区域存在于桥墩处左边x=29~32 m、右边x=33~36 m,桥墩x=32~33 m处为接触区。这是由于3号桥墩沉降,底座板在重力作用下产生垂向位移,引起梁体的转动,使得底座板在2号桥墩附近位置有少量上挠。同时,桥梁由于3号桥墩沉降而下沉,桥梁转动使第2跨桥梁的左端点处(即2号桥墩处)有少许的抬起,使得该桥墩位置的桥梁与底座板相接触。图11中,当沉降量为5~35 mm时,脱空区域的范围和底座板与桥梁的间距大小随沉降量增加而增加。
如图12所示,在沉降发生处(x=65.2 m),脱空区域范围和间距大小随沉降量的增大而增大,呈对称结构,最大间距发生在沉降处(x=65.2 m),不同沉降量对应的数值如表2所示。

图12 3号桥墩处底座板到桥梁板的间距

表2 不同沉降量的脱空区域参数
由表2可知,脱空区域的大小随沉降量增加而增加,但随着沉降量的增加,范围的增加量减少;间距随沉降量增加而增加,并且最大间距值的变化量随着沉降量增加而增加。原因是底座板由于纵向联结特性,在刚度可承受范围内随着沉降量的增加,变形会达到一个最大值,达到这个限值后,脱空区域范围不再随沉降量增加有明显变化。
桥梁的面刚度一般在1 000~2 000 MPa/m,取沉降量为30 mm,研究不同桥梁面刚度下,对底座板脱空区域的影响,如图13、图14所示。

图14 不同桥梁面刚度对3号桥墩处底座板脱空区域的影响
如图13所示,2号桥墩附近位置的底座板脱空区域和空隙大小,随着桥梁面刚度增大而增大,其数值如表3、表4所示。

图13 桥梁面刚度对2号桥墩位置底座板脱空区域的影响

表3 桥梁面刚度对2号桥墩左侧底座板脱空区域的影响

表4 桥梁面刚度对2号桥墩右侧底座板脱空区域的影响
由表3、表4可以得出,桥梁面刚度对2号桥墩左右两处脱空区域范围影响不大,影响范围不超过2%,但是底座板与桥梁板之间的最大间距随着桥梁面刚度的增加而增加,最大增幅达到26.3%。
由图14可知,该位置脱空范围随桥梁面刚度的增大而增大,而底座板与桥梁板间的最大间距基本没有变化,数值如表5所示。
由表5可以看出,桥梁面刚度对沉降发生处(3号桥墩处)的脱空最大间距基本没有影响,对脱空范围的影响不超过4%。

表5 桥梁面刚度对3号桥墩位置底座板脱空区域的影响
4 结论
本文对纵连板式轨道条件下桥墩沉降量与底座板脱空区域的关系进行了推导,计算了底座板随桥墩沉降的位移曲线,并加以有限元验证,同时还对不同沉降量、不同桥梁面刚度下底座板脱空区域的变化进行了对比分析。主要结论如下。
(1)由桥墩沉降与底座板脱空区域的映射关系推导的解析模型可用于求解底座板脱空区域问题。相比有限元法,解析法求解速度更快,而且更清楚地描述了钢轨-轨道板-桥梁面板之间的参数关系。
(2)桥墩沉降下,底座板和桥梁板会发生局部脱离,形成脱空区域。脱空区域范围和脱空最大间距随沉降量的增加而增加,但是脱空区域范围的增加量逐渐减小,而间距的增加量逐渐增大。
(3)沉降区外脱空区域的间隙随桥梁面刚度的增大而增大,对于沉降处的脱空区域,桥梁面刚度变化对其影响不大。

