基于近似贝叶斯计算的ARMA模型参数估计
索文莉,李长国
基于近似贝叶斯计算的ARMA模型参数估计
索文莉,李长国
(陆军军事交通学院 基础部,天津 300161)
将近似贝叶斯计算(ABC)方法应用于ARMA模型的参数估计,并结合实例分析,与其他方法的估计结果相比较,结果表明ABC算法确实较大提高了估计精度。
ARMA模型;近似贝叶斯计算;参数估计
时间序列分析已经广泛应用于工程、科学、社会学和经济学领域中。分析一个时间序列,首先是对所给数据选择一个合适的数学模型,其中自回归移动平均(ARMA)模型是时间序列中最经典的模型,也是最为重要的研究对象之一。ARMA模型的参数估计问题更是在模型建立中一直都占据着重要地位。
极大似然估计和最小二乘估计是最常用的参数估计方法[1],对于相对复杂的ARMA模型,似然函数也会相应更加复杂,很难得到有效的数值计算结果,误差较大,估计的精确度不够高;朱慧明等[2]提出运用基于Gibbs抽样的Markov Chain Monte Carlo贝叶斯方法,王红军[3]也运用贝叶斯方法分析了稳定分布噪声的ARMA模型,但均需要写出似然函数,并要求必须写出后验分布的条件分布,对于似然函数冗繁的情况同样存在困难;为了提高精确度,邓自立[4]提出两阶段的最小二乘方法,但是收敛率相对较低;黄艳勇等[5]提出了一种非线性估计方法,通过DFP算法实现ARMA模型的参数估计,但精度还有待提高。
本文提出将近似贝叶斯计算(Approximate Bayesian Computation,简写为ABC)方法的拓展算法ABC-SMC(Sequential Monte Carlo)算法应用于ARMA模型的参数估计,并结合文献[5]中的实例,比较两种方法的估计结果表明ABC算法得到的估计精度更高。
1 近似贝叶斯计算方法
近似贝叶斯计算是一类新的似然自由方法,基于拒绝方法产生参数的近似后验分布样本。ABC方法将似然函数的数值计算转化为观测数据与一定参数条件下模型产生的模拟数据之间的相似度,这样只需要了解模型的内在构造和数据的生成机理即可。
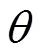
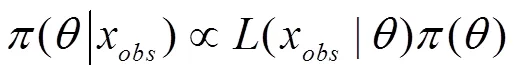
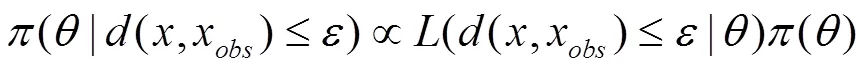
此时ABC算法得到的结果就是真实的后验分布。由式(1)可以看出,值越大,ABC后验分布距离真实后验分布越远;值越小,ABC后验分布越接近真实后验分布,但随着取值的减小,接受率也会逐渐迅速下降。因此最基础的ABC算法接受率普遍较低,给实际应用造成了困扰。
Beaumont[8]提出将回归方法应用于ABC参数估计中,考虑参数与充分统计量之间的回归关系,从而弱化了的取值要求。Toni[9]将序列蒙特卡洛(SMC)思想与ABC算法结合,称为ABC-SMC算法。在该算法中,定义阈值为一个序列,满足
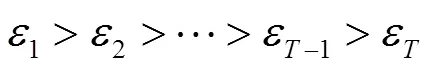
每一次迭代都利用上次的结果,大大提高了效率,且能够保证估计精度。
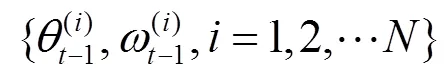
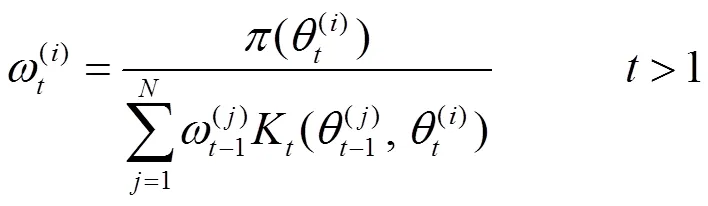
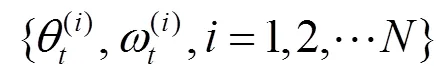
依次下去,最终得到第次迭代参数的后验样本
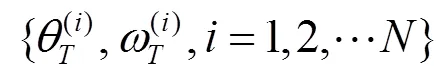
则以其加权平均作为参数的后验估计。综上所述,ABC-SMC算法流程如下:
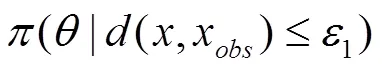
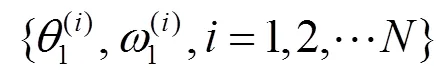
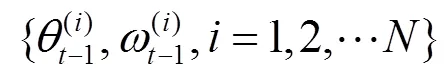
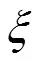
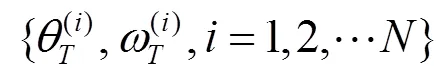
2 实例分析
为验证ABC算法是否能提高ARMA模型参数估计精度,引用文献[5]中给出的ARMA(2,2)模型
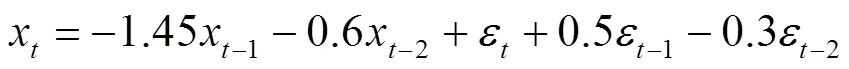
给定初始值1=0,2=0,误差s=0.01,对上述模型采用蒙特卡洛方法模拟生成一组容量为的数据作为观测值,本文取=500。
设ARMA(2,2)模型(3)中参数依次为a,b,c,d,各参数先验分布均为(-5,5),每次迭代生成个粒子,此例中取=100,定义模拟数据与观测数据的距离函数为
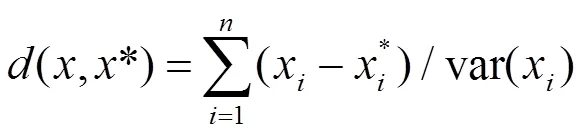
阈值序列为
根据ABC-SMC算法编程计算,可得各参数的后验直方图,如图1所示。
考虑到模型的随机性,将ABC-SMC算法重复100次,每次均取后验样本的加权均值作为参数估计值,则可得到100组估计结果,再取其平均作为最后的参数估计值。与文献[5]中的参数估计结果进行比较,如表1所示,可见ABC-SMC算法显著提高了参数的估计精度。
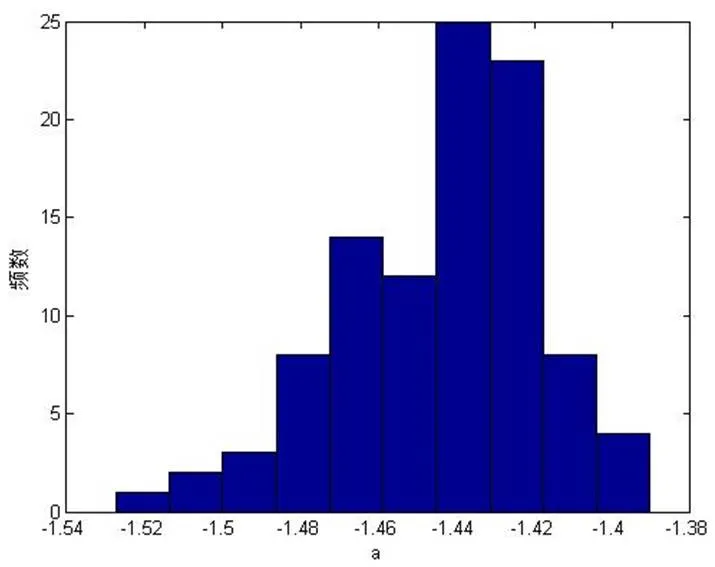
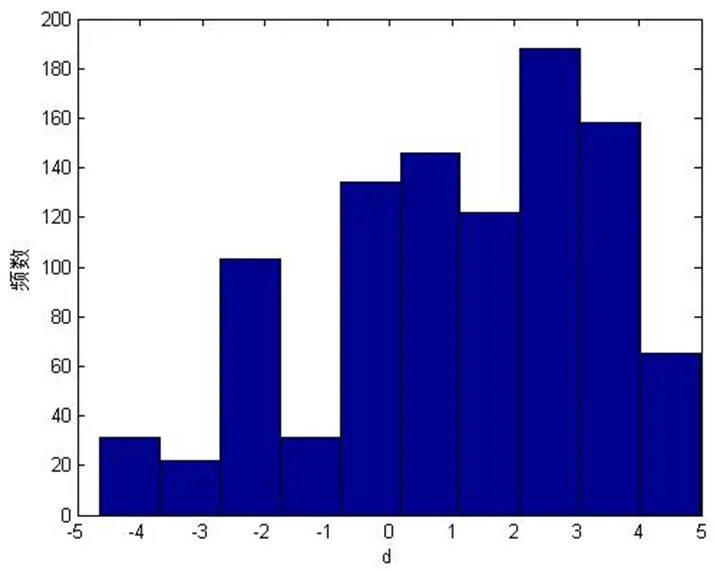
图1 参数a,b,c,d的后验样本直方图
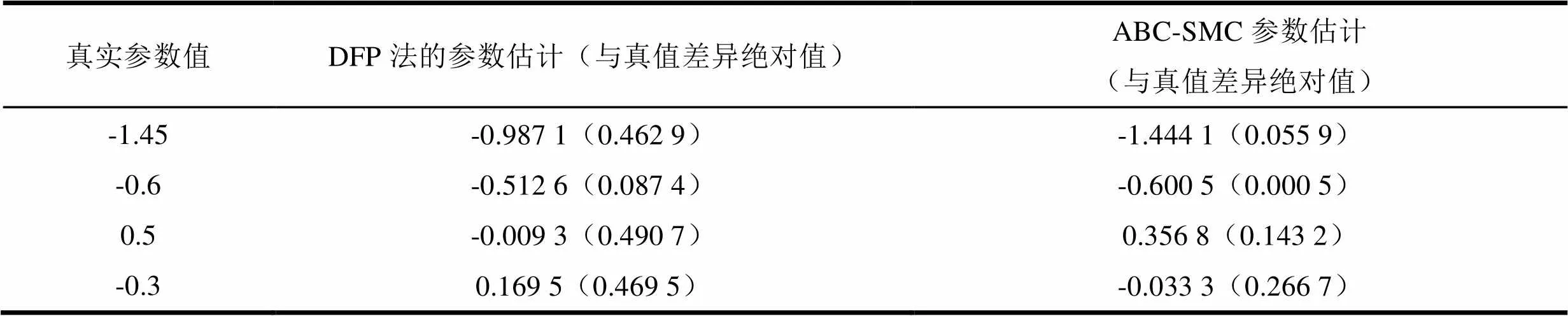
表1 ARMA(2,2)模型的参数估计结果比较
3 结语
将近似贝叶斯算法应用于时间序列ARMA模型中,并以实例说明此算法确实提高了参数的估计精度。ABC-SMC算法将阈值定义为一个递减序列,每一次的抽样都基于上一次的迭代结果,提高了参数后验样本的抽取效率,且估计精度较高。
[1] Perter J. Brockwell, Richard A. Davis.时间序列的理论与方法[M].第二版.田铮,译.北京:高等教育出版社,2001:60- 69.
[2] 朱慧明,邓迎春.基于Gibbs抽样的贝叶斯稳健ARMA模型研究[J].经济数学,2009,26(2):82-90.
[3] 王红军,汤银才.具有稳定分布噪声的ARMA模型的贝叶斯分析及应用[J].应用数学学报,2017,38(3):466-476.
[4] 邓自立,马建为,杜洪越.ARMA模型参数估计的两段最小二乘法[J].科学技术与工程,2002,2(5):3-5.
[5] 黄雁勇,王沁,李裕奇.ARMA模型参数估计算法的改进[J].统计与决策,2009,25(16):7-9.
[6] Pritchard J K, Seielstad M T, Perez-Lezaun A, et al. Population growth of human Y chromosomes: a study of Y chromosome microsatellites[J]. Molecular Biology & Evolution, 1999, 16(12): 1791-1798.
[7] Tavaré S J, Balding D J, Griffiths R C, et al. Inferring coalescence times from DNA sequence data[J]. Genetics, 1997, 145(2): 505-518.
[8] Beaumont M A, Zhang W, Balding D J. Approximate Bayesian computation in population genetics[J]. Genetics, 2002, 162: 2025-2035.
[9] Toni T, Welch D, Strelkowa N, et al.Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems[J]. Journal of The Royal Society Interface, 2009, 6(31): 187-202.
Parameter Estimation Based on Approximate Bayesian Computation for ARMA Model
SUO Wen-li, LI Chang-guo
(General Courses Department, Army Military Transportation University, Tianjin 300161, China)
In this paper approximate bayesian computation method was adopted to estimate the parameters of ARMA model, and through the example analysis, the ABC algorithm indeed improved the estimation accuracy compared with other methods.
ARMA model; approximate bayesian computation; parameter estimation
O212.1
A
1009-9115(2021)06-0014-03
10.3969/j.issn.1009-9115.2021.06.004
2021-02-23
2021-11-01
索文莉(1982-),女,河北邯郸人,硕士,讲师,研究方向为数学教育、统计分析。
(责任编辑、校对:赵光峰)

