基于灰色关联改进TOPSIS法的供应商评价分析

段吉莲，廖兴旺，潘晓琳，李莉莉

基于灰色关联改进TOPSIS法的供应商评价分析

段吉莲1，廖兴旺2，潘晓琳1，李莉莉1

（1. 重庆师范大学 数学与科学学院，重庆 401331；2. 重庆市计量质量检测研究院 力学计量检测研究中心，重庆 400707）

提出一种基于灰色系统理论改进传统理想点法的供应商评价方法，即运用层次分析法（AHP）和熵权法对各项评价指标进行主客组合赋权，同时利用灰色关联分析法对传统逼近理想法进行改进，从而构建出一套新的相对贴近度。依据相对贴近度的大小，对各备选供应商的综合评价值进行排序和择优。结果表明：该方法克服了传统单一赋权方法的缺陷，保证了指标权重的客观性，能准确、有效地避免因排序问题带来的评价误差，使其评价结果更为合理。实例分析表明，验证了灰色关联分析法改进TOPSIS法的有效性和实用性，并为以后的供应商评价提供了一种新的选择方法。

层次分析法；熵值法；组合赋权；灰色关联分析法；理想点法

在这个日益复杂多变的市场竞争环境下，企业面临着非常严峻的生存和发展问题，企业迫切需要转变已有的经营模式和理念，引入一种合作共享、互利互赢为理念的新供应链管理模式。而这种供应链管理模式的一项重要内容则是建立战略合作关系，它运行的基础是对供应商进行选择和评价。企业根据自身的发展状况，从众多因素及指标中建立评价指标体系，并通过科学合理的方法，对供应商的综合评价值进行排序，选择最优供应商。

目前，许多研究人员和学者对供应商的选择和评价进行了大量研究，并取得了很大的成果[1]。1996年，Dickson通过发放问卷，对供应商评价指标的问题做了深入地研究，并对这些指标的重要性进行了分析和排序，其中，供应商评价指标体系中“非常重要”的指标是产品质量，其次就是交货期、价格、历史业绩等方面的指标[1]。Weber等人研究了74篇关于供应商选择与评价的相关文献，得出的研究结果表明，价格在这些研究文献中大约占80%，是讨论的最多的一项准则，并且总结归纳了所有的基本选择方法，主要包括线性权重法、AHP法、DEA法、灰色关联系数法、TOPSIS法、BP神经网络算法、线性规划法和混合整数规划法等[2]；Liao等人通过分析总结得出产品的价格、质量、交货准时率是供应商评价指标重要的因素[3]；张卓根据各种属性的特点，将混合信息统一地进行了规范化处理成为一个区间值函数，并通过结合TOPSIS对方案进行综合分析排序[4]；陈可嘉提出了利用GI－TOPSIS方法确定的供应商评价模型[5]；胡永宏等人采用改进的TOPSIS法对符合市场经济与环境标准的供应商进行综合评价[6]。

本文首先利用层次分析法和熵值法两种计算方法对各指标进行组合赋权，这种组合方法尽可能考虑各个指标的主客观影响因素，更容易体现各个评价指标之间的主客观差异，使得计算权重更加准确。然后采用灰色关联分析法对传统的TOPSIS法进行改进，建立供应商选择评价模型，克服了传统TOPSIS法无法判断内部因素变化态势的缺点，具有较强的灵活性和预测性，使评价结果客观性、严谨性更强。

1 供应商评价指标体系的构建

1.1 供应商评价指标体系建立的原则

建立供应商评价指标体系要考虑很多重要因素，并且要能够准确、全面、系统地反映出供应商的各方面的状况。所选指标体系应适当适中，简洁清晰，数据真实可靠，使其构成一个层次分明的整体，以便准确反映供应商的发展现状和供应商发展前景。同时各企业选择供应商应有不同的侧重点，还应针对不同的发展阶段调整、考核评价指标体系中指标数量和指标内容等，以确保评价结果的稳定性和可比性。

1.2 评价指标体系的构建

供应商评价指标因素选择过程中必须要考虑实际因素，比如价格、质量、成本等。本文将根据重要程度及最终目的，结合以往的供应商评价指标体系，将供应商选择所考虑的因素定义为产品优势、企业能力、资源管理3个维度作为准则层。为了更加切合实际还必须筛选出更多指标，综合考虑多个决策因素，选择了表1所示的十二个评价指标。

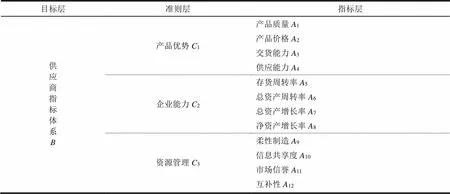
表1 供应商评价指标体系

2 供应商选择评价方法

2.1 基本假设及指标预处理[7]

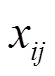
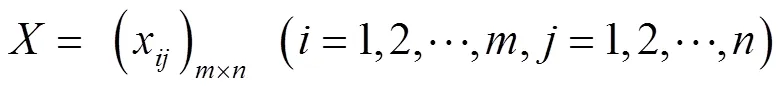
由于各个评价指标间的计量单位、量纲、含义都不一样，为便于统一分析，使用极差变换法对所有需要评价的指标都做出了一个标准化的处理，得到了一个规范化的决策矩阵

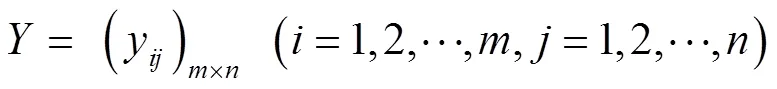
对于效益型指标，如式(2)所示。

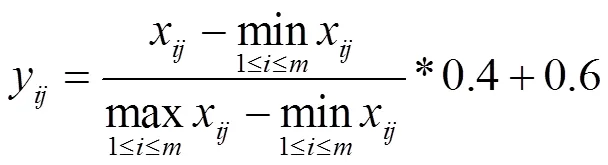
对于成本型指标，如式（3）所示：

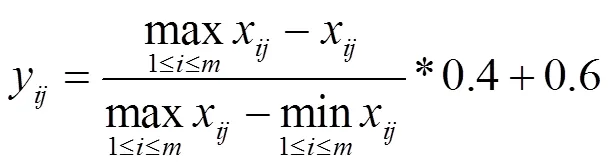
2.2 评价指标组合赋权方法[8]

评价指标权重的计算方法可分为主观赋权和客观赋权。通常，采用主观赋权法，能充分运用专家的知识和实践经验，但评价过程中受主观因素的倾向性，评价结果不够科学准确。而仅靠客观赋权法又无法反映专家对评价指标本身的偏好程度，忽略了评价指标本身的重要性。因此，为使评价指标的权重变得更具有可信度，权重更接近实际，本文采用层次分析法和熵权法两种主客观权重结合的方法组合赋权，确定各个指标的综合权重，避免了只采用单一方法的局限性，得到较为科学性的评价结果。

2.2.1 主观赋权法——层次分析法[9]

层次分析法（AHP）法是一种解决具有多个目标的复杂问题的决策分析方法，这种方法能够有效地解决许多实际问题，它的应用范围广泛，具有高可靠性、低误差等特点。通过相关领域的专家来评判同一级别的每个指标对上一级指标的重要性，形成两两比较判断矩阵，并相应赋予一定的权衡值，最后对判断矩阵进行一致性检验，求得各层次指标的权重j，具体步骤如下。

第一步，创建层次分析结构（根据元素间的相互关系和隶属关系形成多个层次）；

第二步，构造两两判断矩阵（通过专家打分的方式两两进行比较并赋值），包括以下几个方面：

（1）判断矩阵的性质

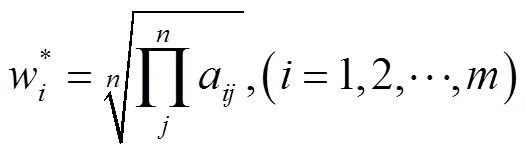
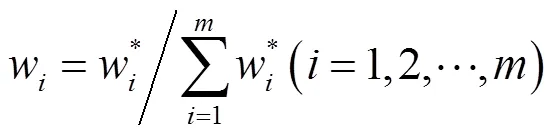
（4）判断矩阵每列求和：

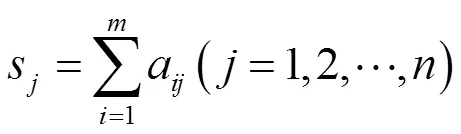
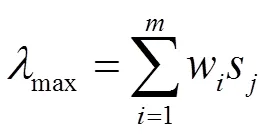
第三步，进行一致性检验：

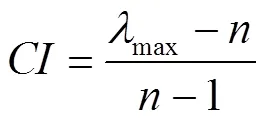
（2）计算一致性比例：

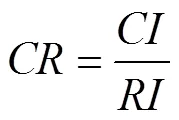
2.2.2 客观赋权法——熵权法

熵权法也称熵值法[10]，可用于任何评价系统中，是一种客观赋权方法。该方法是使用决策矩阵所提供的信息为基础来计算权重，而不是简单地引入决策者的主观偏好来判断，大大降低了主观因素带来的影响。利用熵权法求解客观权重的计算步骤如下：

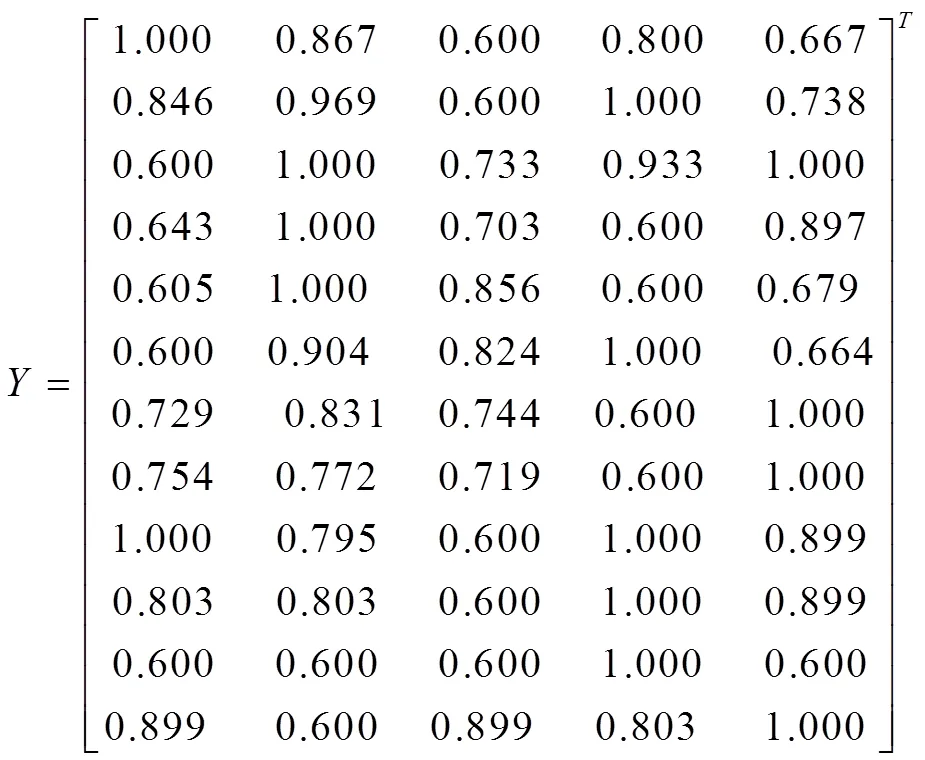
第一步，计算第项指标的熵值：

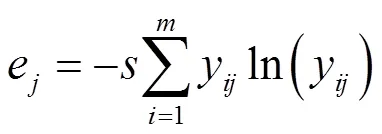
其中，

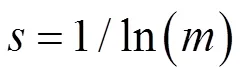
第二步，确定第个指标的差异系数：

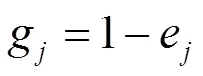
第三步，确定第个指标的客观权重：

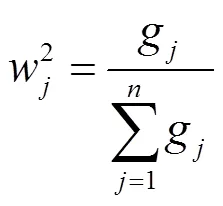
2.2.3 组合权重的确定

组合赋权的思想是将专家经验与客观数据相结合，使得最终确定的组合权重更好地反映评价系统的真实情况。当然，从本质上来讲，不同的赋权方法是从不同的角度进行综合评价，本文是根据层次分析法和熵值法所得的主客观权重进行组合赋权，得到最终的指标综合权重：

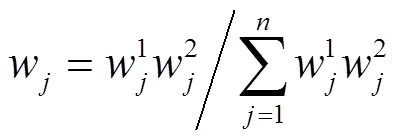
2.3 灰色关联改进TOPSIS法[11-14]

TOPSIS方法主要依据每个备选供应商与理想解的关联程度对各备选供应商进行综合排序。通过规范化初始数据，不仅可以避免由指标量纲带来的不同影响，还可以充分利用原始数据信息，用各方案间的差距来分析备选方案，该方法具有直观、简单、可靠等优点。

灰色关联分析法是一种根据指标之间动态发展态势的相互依赖程度来权衡指标间关系程度的评价方法，这种方法的主要思路是对其关联程度与数据之间的联系进行分析和判断，其中很重要的一步是计算其灰色关联系数。灰色关联系数越大，则相对应的备选供应商的竞争能力越强。这种方法不只是一个简单的结果排序，还能帮助供应商找到自身的优势和劣势，便于合理规划企业接下来的战略发展。其实施步骤如下：

第一步，确定加权规范化决策矩阵

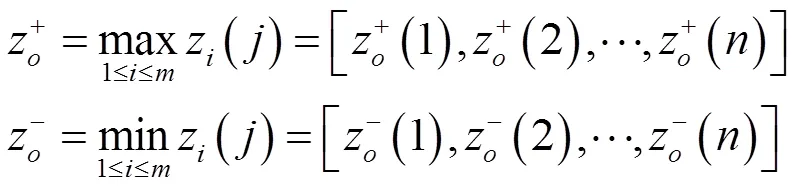
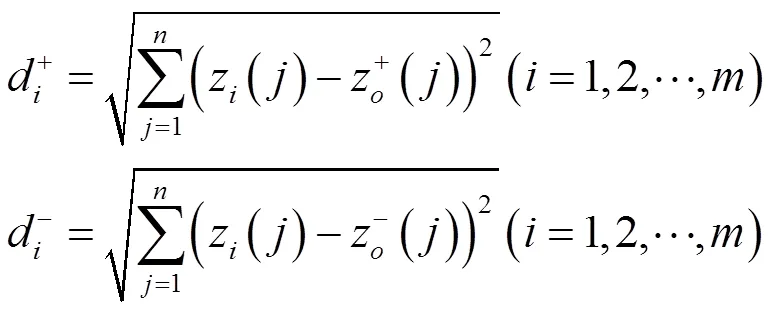
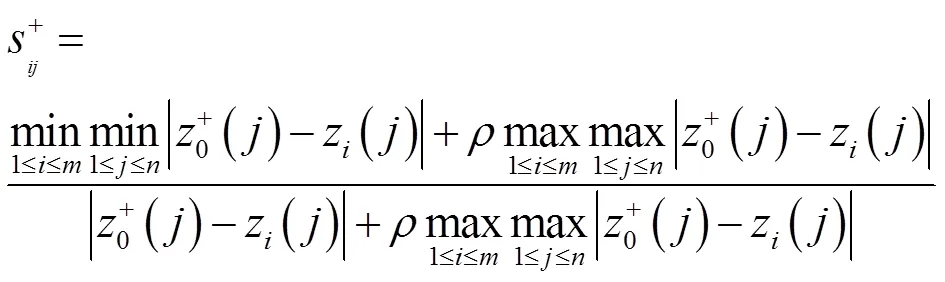
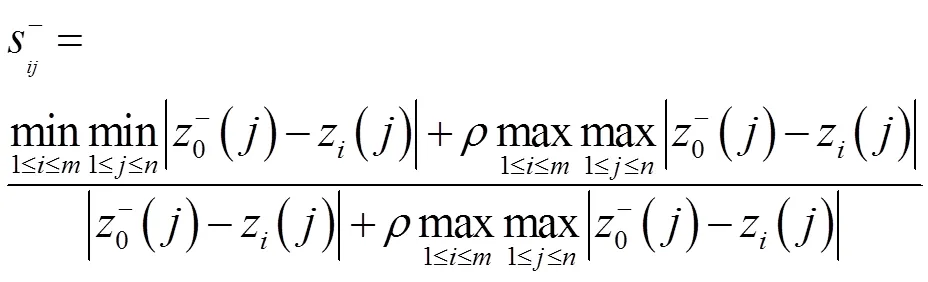
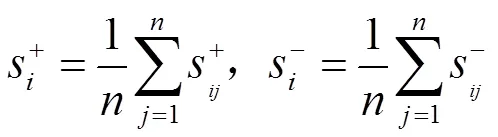
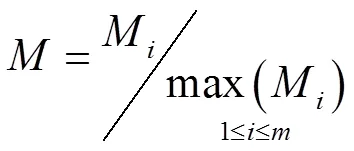
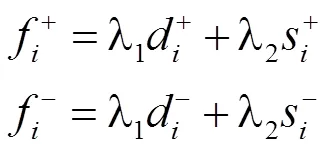
3 实际应用

3.1 企业概述

作为一家汽车制造企业，M公司以高质量、高性能及高品位处在技术领先和市场领先地位。随着市场经济的不断发展和客户个性化需求的发展，M公司发现其目前主要汽车零部件的采购模式及供应商关系管理模式已经不再适应当前竞争市场的需求，M公司决定重新选择零部件供应商。M公司收集了备选供应商各个方面相关的资料，并根据企业实际情况，从众多指标因素中挑选了3个一级指标和12个二级指标，其中，产品优势（1）、企业能力（2）、资源管理（3）为一级评价指标，（1，2，…，12）为二级评价指标，邀请了不同领域专家组成评价小组对5个供应商（1，2，3，4，5）进行评价。通过收集大量资料，各个供应商的指标评价值如表2所示。

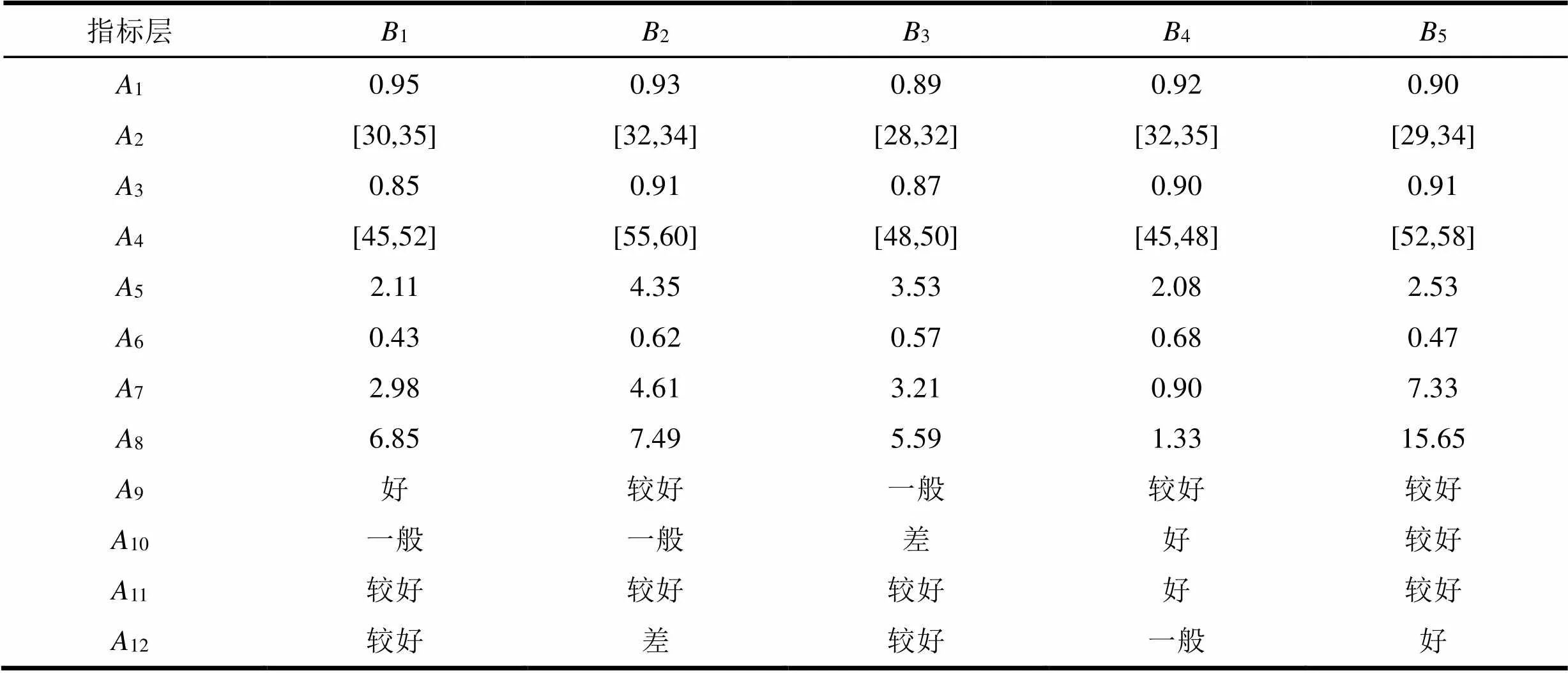
表2 供应商评价指标一览表

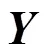
3.2 确定各指标权重

利用层次分析法，邀请专家学者对5个供应商的各个指标进行两两比较，构造准则层、指标层，各个因素的判断矩阵分别为1～，1～，2～，3～，根据公式(4)-(9)确定其主观权重和一致性的检验。各指标判断矩阵如表3-表6所示。

表3 B1～C判断矩阵权重和一致性检验

表4 C1～A判断矩阵权重和一致性检验

表5 C2～A判断矩阵权重和一致性检验

表6 C3～A判断矩阵权重和一致性检验

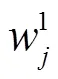
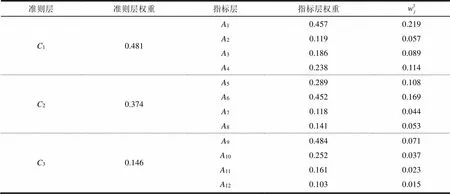
表7 各指标最终主观权重

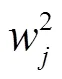
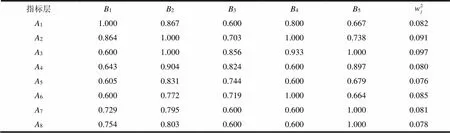
表8 标准化矩阵和客观权重

（接续表8）

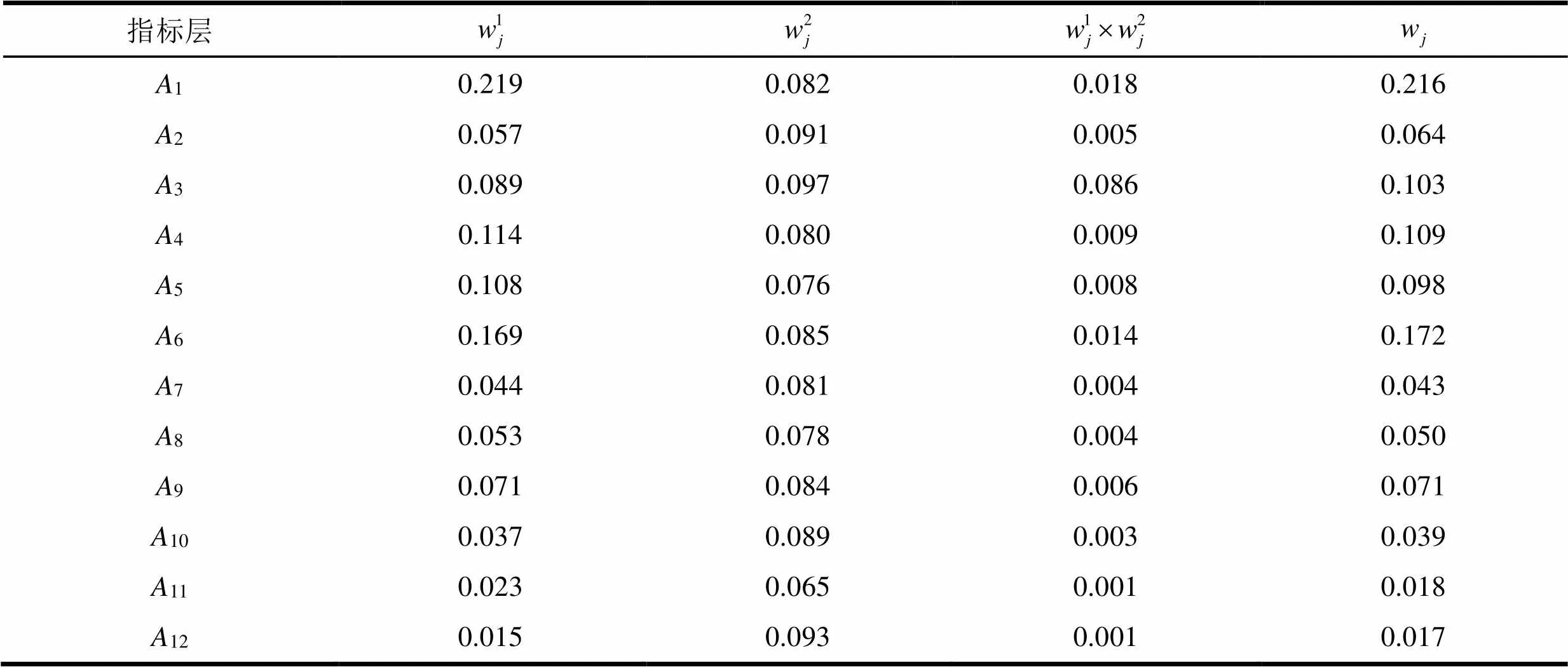
表9 组合权重

3.3 灰色关联改进TOPSIS法对供应商评价

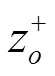
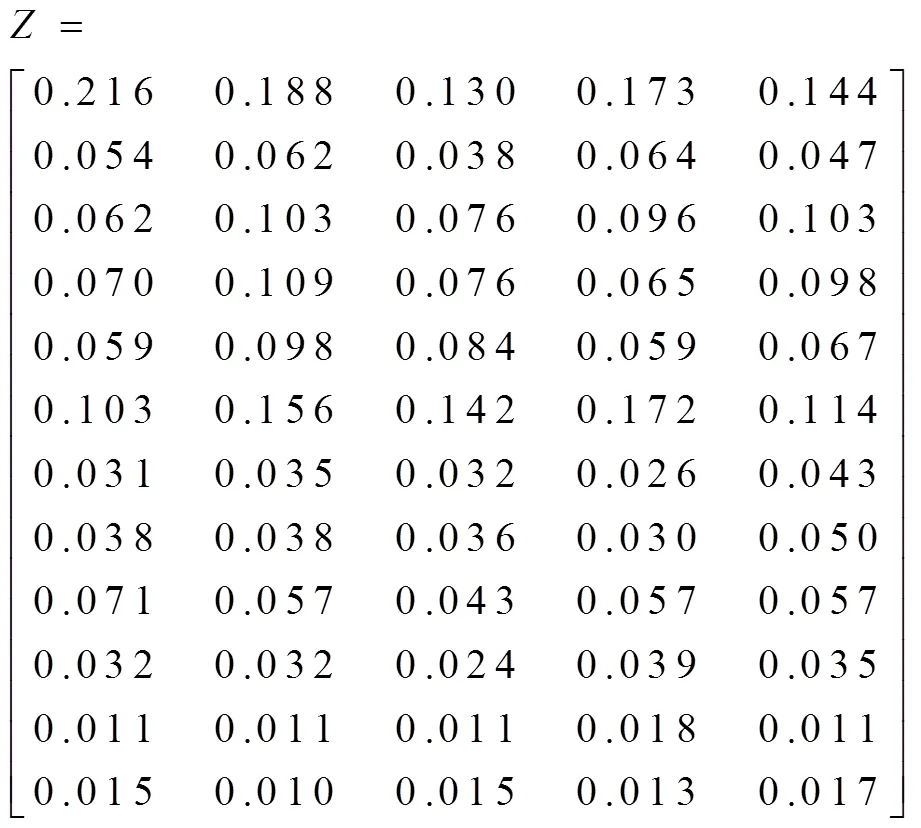
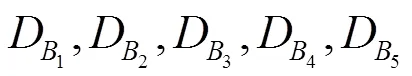
从以上所有计算结果可知，五种供应商选择方案的灰色关联相对近似度计算结果为

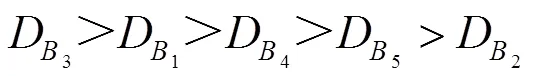
而利用传统的TOPSIS法计算的供应商

相对贴近度为：

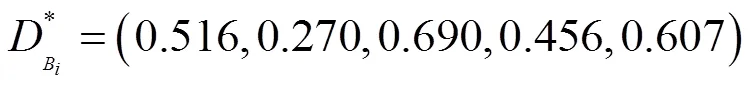
其结果表示为：

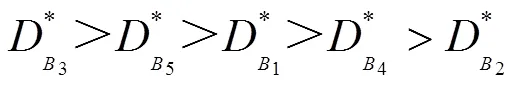
4 结束语

本文结合我国汽车制造业的发展趋势，综合考虑市场需求，选择了产品优势、企业能力和资源管理三个主要影响因素作为汽车零部件供应商的评价指标体系。该评价指标体系较全面地反映了供应商选择的主要影响因素。与现有的评价方法相比，该方法不仅能反映出各备选供应商的整体状况，还可以反映出各供应商内部影响因素变化趋势与理想方案之间的差异。因此，两种方法的结合，为企业提供了一种有效的供应商选择方法，提高了决策的客观性和准确性，是一种更加可行，有效的评价方法。

[1] Dickson G W. An Analysis of Vendor Selection System and Decisions[J]. Journal of Purchasing, 1966, 2(1): 5-17.

[2] Weber C A, Current J R, Benton W C. Vendor Selection Criteria and Methods[J]. European Journal of Operational Research, 1991, 50: 2-18.

[3] Liao C N, Kao H P. An integrated fuzzy TOPSIS and MCGP approach. to supplier selection in supply chain management[J]. Expert Systems with Applications, 2011, 38(9): 10803-10811.

[4] 张卓.混合信息的多属性决策研究[J].计算机与数字工程, 2014,42(12):2433-2438.

[5] 陈可嘉.GI-TOPSIS方法在逆向物流供应商选择中的应用[J].中国流通经济,2014,28(3):39-48.

[6] 胡永宏.对TOPSIS法用于综合评价的改进[J].数学的实践与认识,2002,32(4):572-575.

[7] 李勇,何蕾,庞传军,等.基于层次分析法的火电厂运行情况量化评价方法[J].电网技术,2015,39(2):500-504.

[8] 罗毅,李昱龙.基于熵权法和灰色关联分析法的输电网规划方案综合决策[J].电网技术,2013,37(1):77-81.

[9] 李力,陈宏,王进发.基于模糊层次分析法的军品供应商选择体系研究[J].管理学报,2007,4(1):40-47.

[10] 张军,梁川.基于灰色关联系数矩阵的TOPSIS模型在水环境质量评价中的应用[J].四川大学学报(工程科学版), 2009,41(4):97-101.

[11] 陶瑞.基于Vague集的理想解和灰色关联结合的决策方法及应用[J].数学的实践与认识,2015,45(15):258- 266.

[12] 刘思峰,蔡华,杨英杰,等.灰色关联分析模型研究进展[J].系统工程理论与实践,2013,33(8):2041-2046.

[13] 陈晓红,李喜华.基于直觉梯形模糊TOPSIS的多属性群决策方法[J].控制与决策,2013,28(9):1377-1388.

[14] 孙晓东,焦玥,胡劲松.基于灰色关联度和理想解法的决策方法研究[J].中国管理科学,2005,13(4):64-68.

Supplier Evaluation Analysis Based on Gray Correlation and Improving TOPSIS Method

DUAN Ji-lian1, PAN Xiao-lin1, LI Li-li1, LIAO Xing-wang2

(1. School of Mathematics and Science, Chongqing Normal University, Chongqing 401331, China; 2. Mechanics Metering & ChecKing Research Center, Chongqing Quality Inspection Researcher, Chongqing 400707, China)

On the basis of the existing research and evaluation methods, a supplier evaluation method based on gray system theory to improve the traditional ideal point method was proposed. A reasonable supplier evaluation index system was established by the hierarchical analysis method (AHP) and entropy right method to empower the evaluation indicators. The traditional approaching ideal method was improved by gray correlation. A new relative proximity was build according to the size of relative proximity to sort and select the comprehensive evaluation values of the alternative suppliers. The results showed that the method can accurately and effectively avoid the evaluation error caused by the sorting problem to make the evaluation results more reasonable by overcoming the defects of the traditional single empowerment method and ensuring the objectivity of the index weight. Finally, a new selection method for future supplier evaluation was provided through the example analysis. The effectiveness and practicality of the gray correlation method to improve the TOPSIS method was verified.

hierarchical analysis; entropy method; combination empowerment; gray correlation method; ideal point method

O213.9

A

1009-9115(2021)06-0007-07

10.3969/j.issn.1009-9115.2021.06.003

重庆市教委科学技术研究基金项目（KJ130658）

2021-02-19

2021-11-09

段吉莲（1994-），女，重庆人，硕士，研究方向为数学统计学。

（责任编辑、校对：赵光峰）