零点定理教学研究与设计
赵志红, 傅双双, 苏永美
(北京科技大学 数理学院,北京 100083)
1 引 言
2018年11月24日, 教育部高等教育司司长吴岩在第十一届“中国大学教学论坛”上提出了具有高阶性、创新性和挑战度即“两性一度”的“金课”标准.微积分是大学教学中十分重要的一门公共基础理论课, 肩负着培养学生数学思维, 创新能力的使命, 为其它后续数学以及专业课程的学习打下良好的基础.但微积分课程的教学内容多, 知识难度大, 课时紧张以及大班授课等特点, 使其课堂教学通常剥离实际问题, 主要从理论推导角度讲授, 使得很多知识都不易理解, 导致一些学生失去学习兴趣.所以各大高校的教师们积极探索大学课程的新型教学模式.在新型教学模式下, 教师们不仅要不断的挖掘生活中的有趣案例[1-2], 而且要处理好实际案例与相关数学理论的相互渗透, 这样才可以提高教学效果和教学质量,才有利于学生对微积分基本思想与方法的全面理解和把握, 有利于学生由具体问题到抽象数学思维的转化能力的培养,以及创新性思维, 科学素养的养成.
零点定理是高等数学中连续函数的一个重要性质, 主要用于方程根的存在性证明以及与微分中值定理综合运用, 实际上零点定理还有非常多的实际应用价值.目前, 关于零点定理的课程设计不多, 已有的课程设计主要是定理的简单引入以及一些简单应用[3].笔者发现零点定理是有一定深度和广度的, 可以做到“两性一度”.本文首先从橡皮筋问题引出零点定理, 分析如何从实际问题出发建立数学模型[4], 使学生通过解决橡皮筋问题, 发现零点定理, 这是发现学习的过程.接着, 借助几何直观引导学生证明零点定理, 加深学生对零点定理的理解, 不仅知其然, 而且知其所以然, 这提高了课程的挑战度.进一步将零点定理应用到方镜框问题, 这是一个既有趣味性又能充分体现数学思想方法的例子, 对这个问题的解决不仅可以开拓学生的视野, 引导学生踮起脚尖对高层次的知识进行构建, 而且学生可以认识到一个简单的定理可以解决复杂的问题, 这体现了课程的高阶性.最后提出零点定理的进一步扩展思考, 并引申到了学术前沿问题, 培养学生的创新素质, 引导学生自主探究, 这体现了课程的创新性.在讲解过程中深入浅出的展示一些实际问题背后的数学理论.这个过程不仅可以帮助学生深刻地理解零点定理, 培养学生发现问题、分析问题、解决问题的能力, 而且让学生可以更好地领略数学的深奥与美妙.
2 零点定理的引入
引入是非常重要的环节.如果一开始直接介绍零点定理, 学生会感觉枯燥没有兴趣.为了激发学生的学习兴趣,选用一个有趣味的橡皮筋问题[3]来引入本节课内容.这个问题简单直观, 却蕴含着丰富的数学思想.
引例拉一根橡皮筋, 一头朝左拉, 同时另一头朝右拉, 在橡皮筋不拉断的情况下是否有一点在原来的位置不动?
分析 这个问题直观明了, 提出问题后学生容易理解并给出自己的猜测.但是, 为了科学严谨地回答这个问题, 还需要把它抽象成一个数学问题, 通过建立数学模型[4]对这个问题进行分析和回答.实际上, 分析这个数学问题的过程就是零点定理学习的过程.
模型假设 对橡皮筋进行必要的假设: 橡皮筋为一维直线段.
模型构建 引导学生用数学语言把拉橡皮筋时的条件和结论表示出来.
由模型假设, 可以将橡皮筋放置在x轴上, 橡皮筋上各点位置用x表示, 即x∈[a,b].橡皮筋拉开之后各点的位置为f(x), 在橡皮筋拉伸的过程中, 函数f(x)是连续变化的, 且拉伸后橡皮筋的左端点满足f(a)

图1 橡皮筋拉伸示意图
命题如果函数f(x)是区间[a,b]上的连续函数, 满足f(a)
几何分析 构造辅助函数F(x)=f(x)-x,x∈[a,b], 则F(x)是闭区间[a,b]上的连续函数, 且满足F(a)<0,F(b)>0.从几何角度出发简单的分析一下, 辅助函数y=F(x)在区间[a,b]上是一条连续的曲线,F(a)<0表示曲线在端点a处的值在x轴下面,F(b)>0表示曲线在端点b处的值在x轴上面, 那么这条连续曲线必然在某一点ξ∈(a,b)穿过x轴, 如图2所示.因此在ξ处有F(ξ)=0, 即ξ=f(ξ).
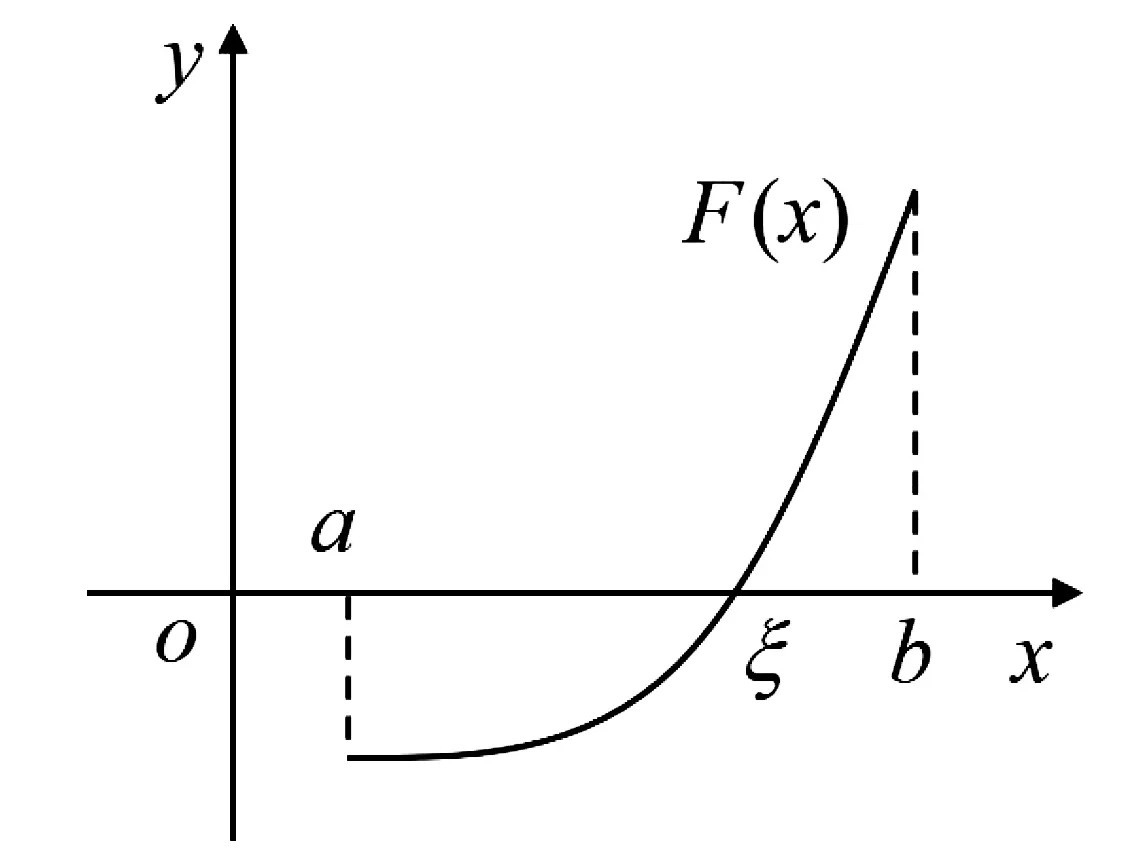
图2 F(x)的图形
问题得证.由此可以自然地引出零点定理.
3 零点定理
3.1 零点定理的内容
零点定理又称为布尔查诺定理, 是由捷克数学家布尔查诺(Bolzano,1781-1848)提出的[5].
零点定理[6]函数f(x)在闭区间[a,b]上连续, 且满足f(a)f(b)<0, 则至少存在一个ξ∈(a,b), 使得f(ξ)=0.
从几何角度, 零点定理说明函数y=f(x)在(a,b)内与x轴至少存在一个交点.从代数角度, 零点定理说明方程f(x)=0在(a,b)内至少存在一个实根.零点定理的证明需要用到实数理论的相关知识, 因此高等数学教材都没有给出证明.但从几何直观角度, 可以引导学生探索分析问题, 如果采用二分法会得到怎样的结果呢?
3.2 二分法证明零点定理
二分法主要是通过不断地把函数的零点所在的区间一分为二, 使区间的两个端点逐步逼近零点, 进而得到函数零点.
二分法求零点的步骤:
函数f(x)满足f(a)f(b)<0, 不妨设f(a)<0,f(b)>0.
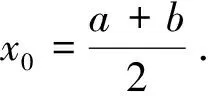
(i)如果f(x0)=0, 则x0就是函数f(x)的零点, 结论得证;
(ii)如果f(x0)>0, 可令a1=a,b1=x0;
(iii)如果f(x0)<0, 则令a1=x0,b1=b;
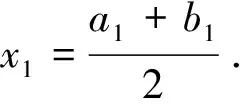
(i)如果f(x1)=0, 则x1就是函数f(x)的零点;
(ii)如果f(x1)>0, 令a2=a1,b2=x1;
(iii)如果f(x1)<0, 令a2=x1,b2=b1;
…………
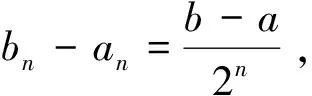
因此f(c)=0.
整个证明过程用到的都是高等数学中学生已知的知识.但老师引导学生“跳一跳”后, 学生是可以理解的.在一定程度上体现了教学的“挑战度”.
3.3 零点定理解题步骤
在高等数学课程中重点在于让学生掌握如何运用零点定理证明函数零点的存在性.运用零点定理解题的步骤:
一、构造连续的辅助函数f(x), 使得问题变为求解方程f(x)=0的根;
二、寻找闭区间[a,b], 使得f(x)在左右端点处的值异号.
4 应用探索—方镜框问题[7]
4.1 问题描述
给定平面上的一条简单的光滑封闭曲线, 能否作一个各边都与曲线相切, 且包含这条闭曲线的正方形?
4.2 问题分析
这个问题比之前的橡皮筋问题复杂很多, 而且涉及到许多概念, 如区域、边界、光滑曲线和相切等.笔者简单解释一下题目中出现的几个概念.简单闭曲线是指平面上一条除起点与终点外, 不自交的连续曲线, 也就是平面上一条没有重点的连续闭曲线, 也称Jordan闭曲线.光滑曲线是指曲线上的每一点处都有切线, 且切线随切点的移动而连续转动[8].
显然, 对于一些特殊的简单光滑闭曲线这个问题是显然成立的, 如圆、椭圆, 见图3.那么对于一般的光滑闭曲线呢?答案也是肯定的.
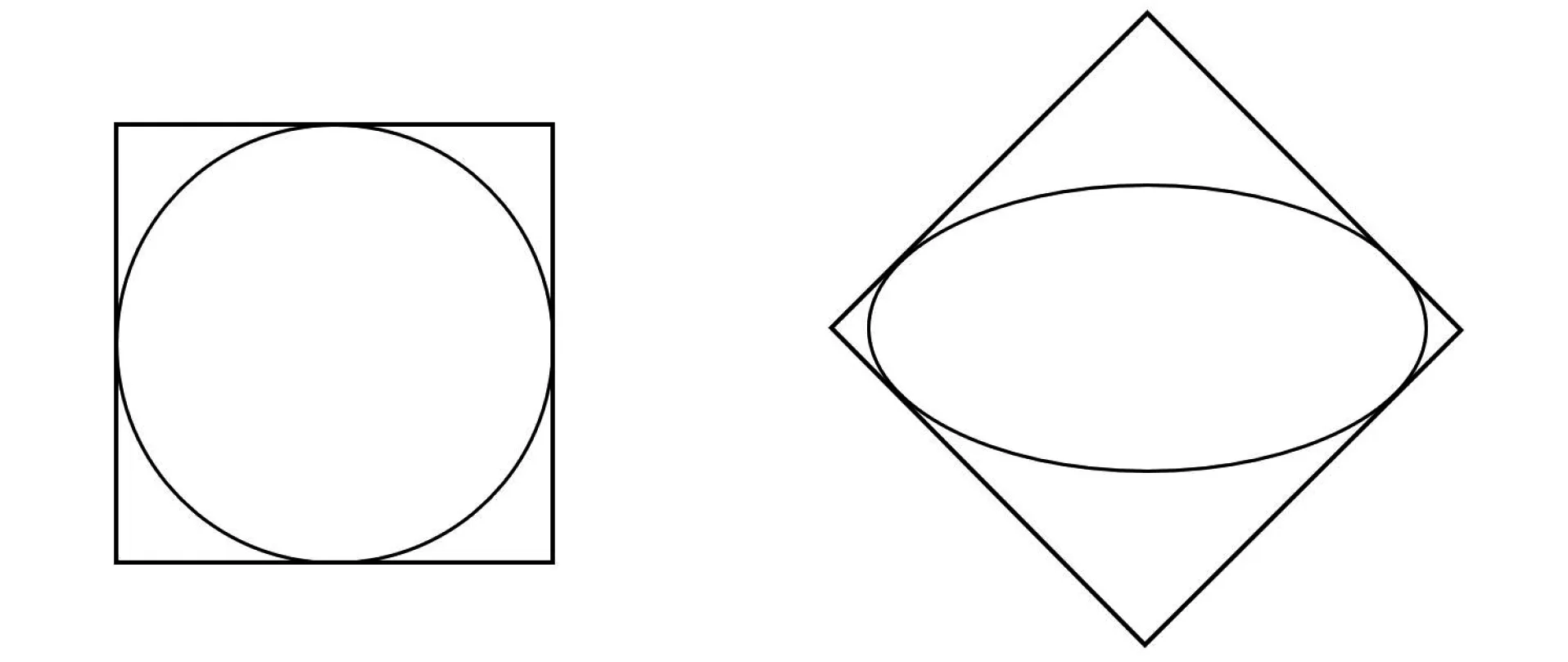
图3 圆(左)、椭圆(右)满足方镜框问题
由于包含闭曲线的方形的边是由闭曲线的切线组成的, 可以引导学生发现一条简单光滑闭曲线及其各点切线有什么样的性质.一条简单光滑闭曲线具有下面两个性质:
性质1简单光滑闭曲线是连续周期函数, 闭曲线上的每一点处都有切线, 且切线随切点的移动而连续转动.
性质2闭曲线上的切线可以组成无数个包含这个闭曲线的矩形, 并且矩形的边长是随着曲线上的点连续变化的.
对于性质1, 建立直角坐标系, 并在闭曲线上任意选定一点(x0,y0), 令s表示从(x0,y0)出发逆时针方向到曲线上任一点(x,y)的弧长, 如图4, 则点(x,y)可以表示为
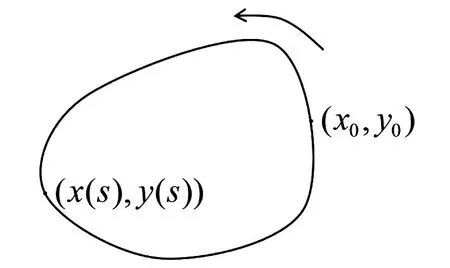
图4 参数表示
令L表示闭曲线的弧长, 则有(x(s+L),y(s+L))=(x(s),y(s)).另外, 由于闭曲线是连续的, 则
即(x(s),y(s))连续, 由此可以看出简单光滑闭曲线是连续周期函数.又由光滑曲线的定义可知曲线上的每一点处都有切线, 且切线随切点的移动而连续转动.
下面分两种情况讨论性质2.为了便于理解, 对曲线的切线规定一个正方向, 即一个人在闭曲线上且面向闭曲线所围区域时, 此人的右侧为切线的正方向.
情形1 闭曲线位于曲线上任一点切线的一侧(图5(a)).将闭曲线上的点都平移到原点, 则闭曲线上的切线形成图5(b), 由于曲线光滑, 所以切线的斜率是连续变化的.那么闭曲线上任取一点, 一定可以找到曲线上其余三点, 使这四个点处的切线相互垂直, 这样过曲线上任一点一定可以找到其余三点, 使得这四个点的切线组成的矩形包含这条闭曲线(图5(c)).由于曲线是光滑的, 所以矩形的边长是随着曲线上的点连续变化的.

图5 情形1
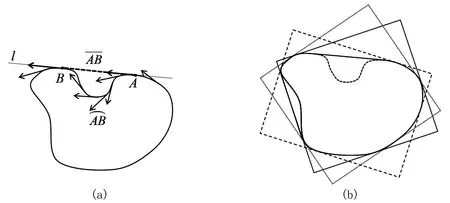
图6 情形2
4.3 问题解答
模型构建 关键问题是用数学语言把包含闭曲线的正方形出现的条件和结论表示出来.
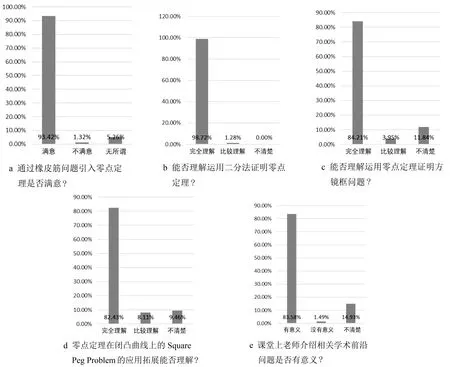
用变量x表示闭曲线上点的位置.由性质1, 设闭曲线的周期为L, 即x+L又回到x.由性质2, 以闭曲线上一点x处的切线为边, 且包含闭曲线的矩形的边长为分别为f(x)和g(x), 如图7所示.边长f(x)对应的切线的切点为x, 边长g(x)对应的切线的切点为x+L1, 矩形与闭曲线的另外两个切点分别为x+L1+L2,x+L1+L2+L3,这里Li>0,i=1,2,3,且L1+L2+L3 图7 矩形的边长 f(x)=f(x+L1+L2),g(x)=g(x+L1+L2), 且当x转到x+L1时得到与原来相同的矩形,于是 f(x+L1)=g(x),g(x+L1)=f(x+L1+L2)=f(x). 这样, 不妨设从x=0开始改变点x的位置, 使包含闭曲线的矩形为正方形可归结为如下数学命题: 命题已知f(x),g(x)为闭区间[0,L]上的连续函数, 满足 f(L1)=g(0),g(L1)=f(0),L1 证明存在一点x0∈[0,L1], 使得f(x0)=g(x0). 模型求解 如果在x=0处满足f(0)=g(0), 则问题得证.如果在x=0处f(0)≠g(0),不妨设f(0)>g(0),构造辅助函数F(x)=f(x)-g(x), 显然F(x)在[0,L]上连续, 且满足 F(0)=f(0)-g(0)>0,F(L1)=f(L1)-g(L1)=g(0)-f(0)<0, 由零点定理, 可得至少存在点x0∈(0,L1), 使得F(x0)=0, 即f(x0)=g(x0).因此, 必存在一点x0∈[0,L1],使得f(x0)=g(x0). 因此, 给定平面上的一条简单光滑闭曲线, 一定可以做一个包含这条闭曲线的正方形并且它的四边都与曲线相切.对方镜框问题的解决在一定程度上体现了教学的“高阶性”, 可以培养学生解决复杂问题的综合能力. (i)给定平面上的一条简单光滑闭曲线, 能否作一个各边与曲线相切, 且包含这条闭曲线的等边三角形? 是否存在满足条件的正五边形, 正六边形, … , 正n边形? (ii)闭凸曲线上的Square Peg Problem: 给定平面上的一条简单光滑的凸(曲线总是位于它的每一点切线的同一侧)闭曲线, 能否做一个内接正方形(正方形各点都在曲线上), 如图8所示.(提示: 模型假设部分可以通过内接直角梯形证明以简单闭凸曲线上任意一点为顶点, 一定存在内接矩形; 然后利用零点定理.) 图8 内接正方形 (iii)上面这个问题是1911年德国数学家Otto Toeplitz提出的Square Peg Problem的简化版.一般的Square Peg Problem描述如下: 平面上任意一条简单闭曲线, 是否存在内接正方形? 这是一个百年老问题至今未解决.2020年新冠肺炎疫情期间波士顿学院的Joshua Evan Greene和英国杜伦大学的Andrew Lobb 两位数学家解决了Rectangular Peg Problem: 平面上任意简单闭曲线存在任意给定长宽比的内接矩形.这个研究成果离Square Peg Problem的结论越来越近了.这样在日常的教学中联系学术前沿, 可以培养学生的“创新性”. 通过“橡皮筋问题”引入零点定理是否有助于提高学生的学习兴趣, 学生能否理解运用二分法对零点定理进行证明以及运用零点定理对“方镜框问题”进行讨论, 拓展到闭凸曲线上的Square Peg Problem以及学术前沿问题学生是否觉得有意义等问题, 笔者针对北京科技大学2020级机械、能源两个专业78名同学进行课堂教学并做了调查问卷, 结果如图9所示.课堂教学实践表明, 学生们全程沉浸课堂, 对本文提出的教学设计有较高的认可度, 教学效果良好. 图9 统计直方图 零点定理是高等数学中的一个重要定理, 在许多数学理论推导中发挥重要作用.本文的教学设计始终贯彻以学生为中心, 根据学生的认知心理特点, 从有趣的问题引导学生发现问题, 探究定理, 并从几何直观的角度引导学生探求定理的证明思路, 最后利用零点定理研究了方镜框问题以及闭凸曲线上的Square Peg Problem, 将经典的微积分理论同科研前沿联系.这样的设计不仅体现了教学上的“两性一度”, 更有助于培养学生的创新思维. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.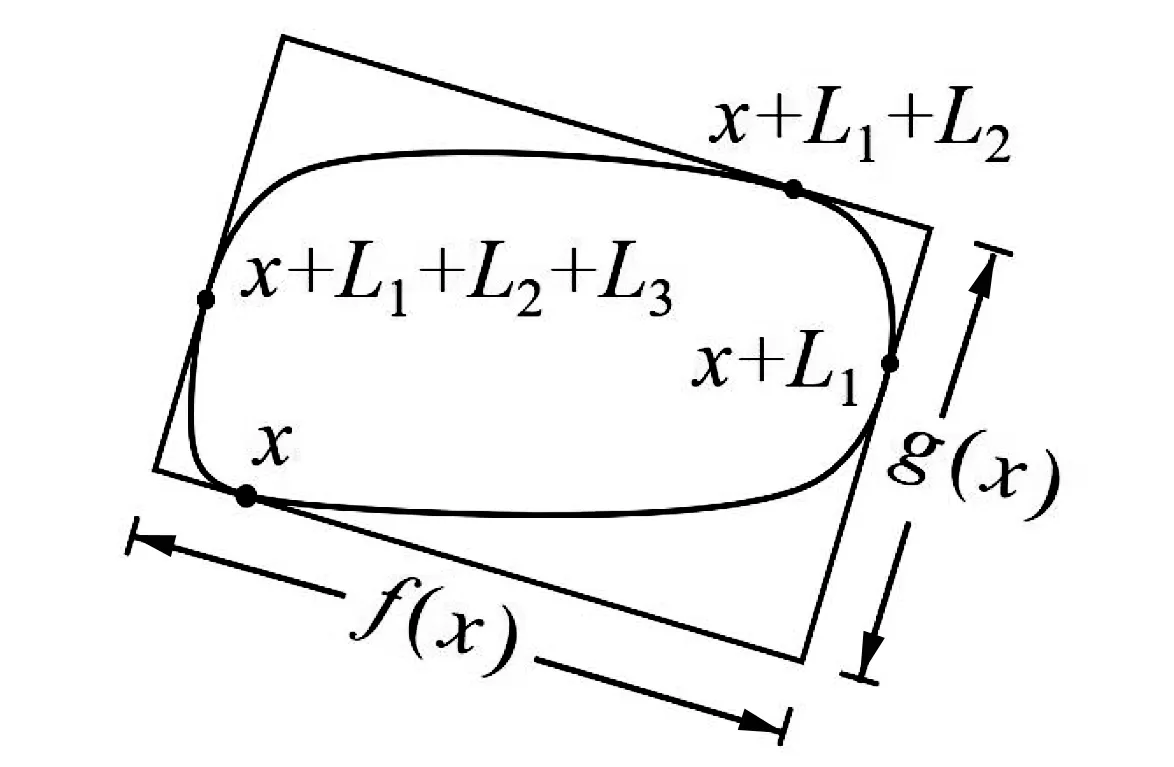
4.4 拓展思考

5 教学效果评价
6 结 论

