高速冲击缓冲装置气液混合流体节流缓冲特性

秦航舵，眭锁炳

（上海船舶设备研究所，上海 200031）

0 引言

高速冲击缓冲装置是某大型船舶缓冲系统的重要组成部分，如图1所示，主要包括缓冲液压缸、蓄能器、流量控制阀等部件。高速冲击缓冲装置先于大型缓冲系统动作，用于保证大型缓冲系统能够更加稳定可靠地工作，其作用时间非常短，整个缓冲过程约为0.3～0.5 s，缓冲时最大运行速度为9～12 m/s，具有高速、大流量和快速响应的特点。为满足高速冲击缓冲装置快速响应的工作需要，蓄能器采用具有容积大、惯性小、反应灵敏等优点的非隔离式蓄能器型式，但其存在气体易混入油液中的问题。在使用过程中，首次缓冲时缓冲液压缸最大压力和蓄能器最大压力相对较低，但完成一次缓冲后蓄能器初始液位急剧升高，再次缓冲时缓冲液压缸最大压力和蓄能器最大压力明显变大，且后续随着缓冲次数的增加压力一次比一次高，这将直接影响到高速冲击缓冲装置连续使用时的性能稳定性。

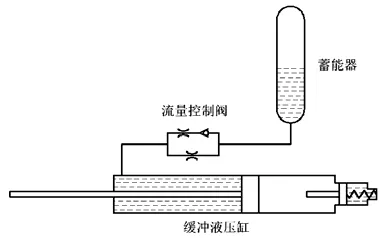
图1 高速冲击缓冲装置结构示意图

气体混入油液形成气液混合流体可能是使高速冲击缓冲装置液压缸压力升高缓冲性能下降的最主要原因。液压缸的压力由流量控制阀节流压降和蓄能器压力决定，气体的混入使得油液通过流量控制阀时由纯液体变成了气液混合流体，使得流量控制阀的节流压降发生变化，进而导致液压缸压力升高。气液混合问题由来已久，关于气液两相流节流压降的研究也有不少，早在1959年SCHUSTER[1]就首次发现两相流流过孔板时前后压差值要比单相液流高，随后MURDOCK[2]通过整理试验数据提出了分相流动模型计算式，BIZON和COLLINS应用MURDOCK方法也分别提出了各自的计算式，克列姆莱夫斯基假设孔板进口处气液两相流速相同提出了中低压工况压降计算式，之后SMITH等[3]、CHISHOLM等[4]也都有关于这方面的研究，但所建立的计算式试验参数都不高，应用范围狭窄。林宗虎[5]以分相流动模型为基础，利用相似理论得出了通用性较广的气液两相流孔板压力降计算式，但也不适用于本文研究的高速冲击缓冲装置的高压高速、大流量、低干度工况。为探究液压缸压力升高的根本原因，本文将从气液混合机理分析入手，通过数学建模、优化改进和试验验证，为解决高速冲击缓冲装置在连续使用后的压力升高问题提供一定的理论参考。

1 气液混合机理分析

非隔离式蓄能器是高速冲击缓冲装置的重要部件之一，在装置缓冲过程中用于储存油液和蓄能，在缓冲结束后用于装置的自动复位，以待下一次的缓冲。非隔离式蓄能器上腔充入压缩空气，下腔充入液压油液，并通过液压管路与缓冲液压缸相连。首次缓冲时高速冲击缓冲装置的油液为纯液体，随着缓冲活塞杆的拉出，从缓冲液压缸排出的油液经流量控制阀进入蓄能器，并挤压上腔的压缩空气从而储存一定的压力能，用于缓冲液压缸的复位。由于高速冲击缓冲装置缓冲过程时间很短，缓冲液压缸活塞杆快速拉出，将缓冲液压缸中油液高速排入蓄能器，因此流入蓄能器的油液流速很快，使得蓄能器下腔的油液突破气液分界面冲入上腔的压缩气体，如图2(a)所示。油液在上升及回落过程中搅动蓄能器上腔的压缩气体，导致大量气体混入到油液中，在蓄能器中形成气液两相流，复位时混入油液中的气体还没来得及析出，就在蓄能器高压气体的推动下，与油液一起通过流量控制阀进入缓冲液压缸，在此过程中，蓄能器、缓冲液压缸以及液压管路中的油液皆以气液混合的两相流形式流动。复位结束后蓄能器的初始液位高度急剧增加，再次缓冲时高速冲击缓冲装置的油液由纯液体变成了气液混合流体，如图2(b)所示。随着高速冲击缓冲装置缓冲次数的增加，油液的气液混合程度逐渐加重，使得气液两相流的含气量逐渐增加，直至气液混合达到饱和为止。

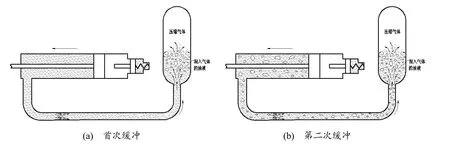
图2 气液混合示意图

2 气液混合流体密度与压力关系分析

一般情况下油液可视为不可压缩流体，其体积弹性模量很大，压缩系数很小。但当油液中混入大量气体后，形成的气液混合流体的体积弹性模量较纯油液相比将大幅降低，且随着压力的变化体积弹性模量会不断变化，进而导致气液混合流体的密度不断变化。下面从体积弹性模量角度分析气液混合流体密度与压力的关系。

分别用Km、KL、KG表示气液混合流体、油液和气体的体积压缩系数，则[7]：

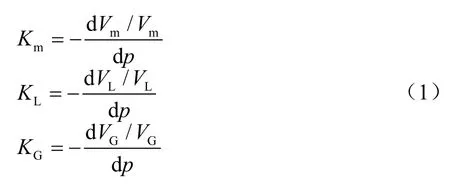
式中：Vm、VL、VG分别为气液混合流体、油液、气体的体积；p为压力。

体积压缩系数K与体积弹性模量E互为倒数关系，即E＝1/K，即：

又因为体积含气率β＝VG/VM，气体等熵压缩时体积弹性模量等于等熵指数κ乘以压力，即EG＝κp，则：

液压油采用水乙二醇，其体积弹性模量EL＝3 450 MPa，一般缓冲时液压缸最大压力p≤25 MPa，当体积含气率大到一定程度时，(1－β) /EL可忽略，故上式可化简为

又根据：

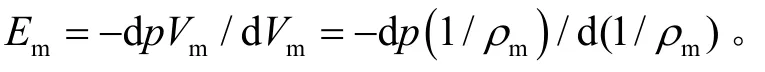
式中：ρm为气液混合流体密度，可得：

令κ/β＝γ，则气液混合流体压力与密度的关系为

式中：ρ1、ρ2分别是气液混合流体在压力p1、p2下的密度。

由式（7）可知，当体积含气率β较大时，气液混合流体基本符合可压缩流体的典型特征。

3 气液混合流体特性分析及建模

在高速冲击缓冲装置缓冲过程中，油液从液压缸有杆腔排出，经流量控制阀节流后流入蓄能器。首次缓冲时经过对装置油液的排气，缓冲液压缸、流量控制阀、蓄能器及其液压管路中油液不含气体，此时油液为纯液体，故按不可压缩流体来建立缓冲过程数学模型。但在首次缓冲后，由于蓄能器油液中混入大量气体形成气液混合流体，且随着自动复位过程，该气液混合流体进入到缓冲液压缸中，此时此刻缓冲液压缸内流体不再是不可压缩的纯液体，而是可压缩的气液混合流体。再次缓冲时大量气体的混入造成气液混合流体弹性模量大幅降低，气液混合流体密度也降低，考虑到缓冲过程速度很快，故采用均相流动模型，即气液混合流体密度等效为单一密度，并考虑气体混入油液造成液压介质可压缩，按可压缩流体来建立缓冲过程数学模型。

3.1 气液混合流体节流特性分析

气液混合流体节流缓冲示意如图3所示，截面1-1面积为A1密度为ρ1速度为v1，截面2-2面积为A2密度为ρ2速度为v2，气液混合流体具有一定的压缩性，在流动过程中流体密度非一成不变，即ρ1≠ρ2，下面对其节流特性进行分析。

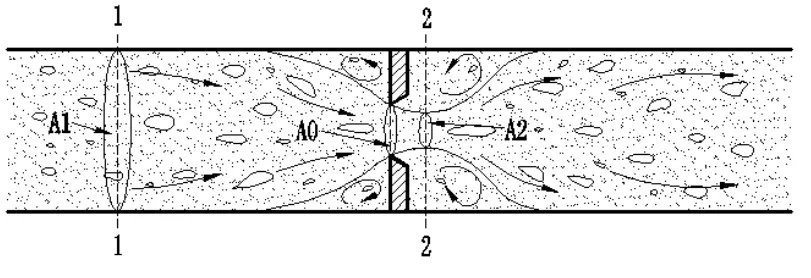
图3 气液混合流体节流示意图

根据可压缩流体定常流动伯努利方程可得：

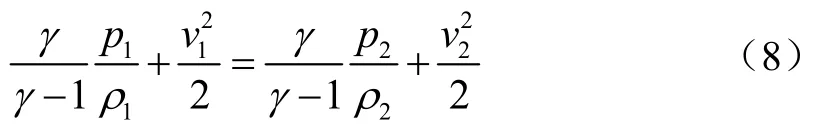
用qM表示质量流量，结合质量流量连续性方程ρ1v1A1＝ρ2v2A2＝qM＝常数，可得：

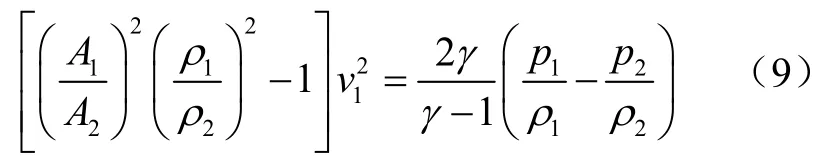
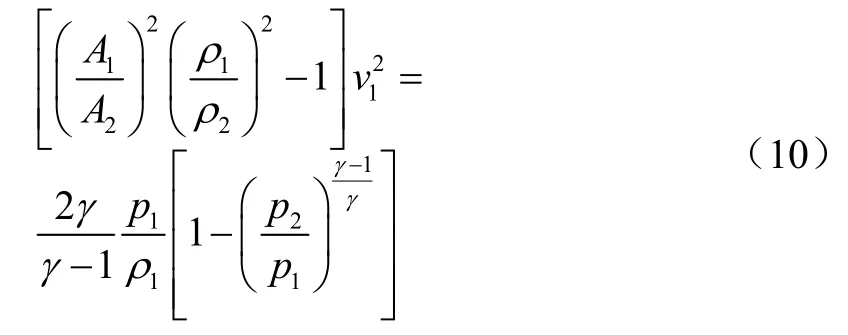
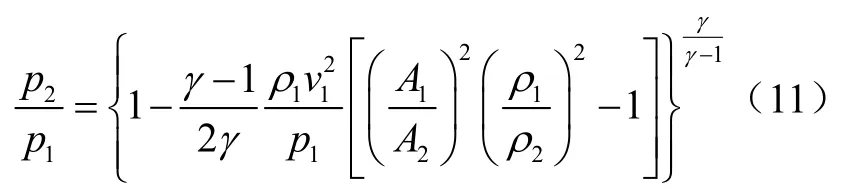
忽略x2以后的高次项并将x重新代入，整理可得：

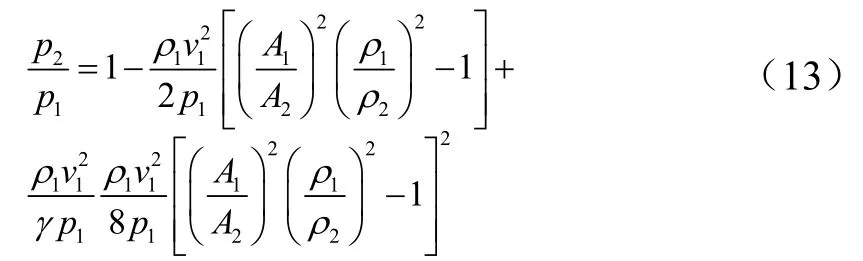
令M＝ρ1v1/(γp1)，并引入流束收缩系数Cc＝A2/A0，可得压力p1的计算公式为

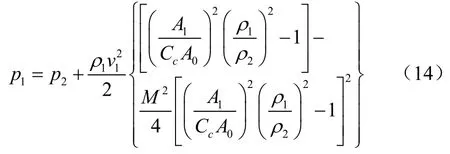
故质量流量的计算公式为

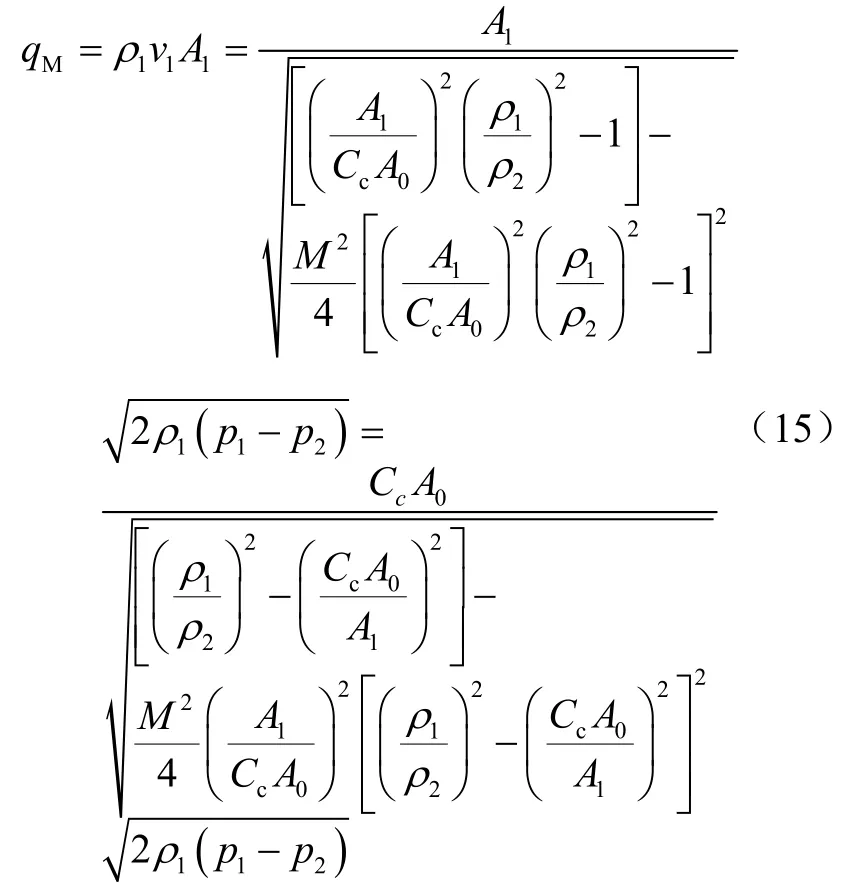
式中：ρ1/ρ2≥1，CcA0/A1＜＜ρ1/ρ2可忽略，故质量流量公式可简化为：

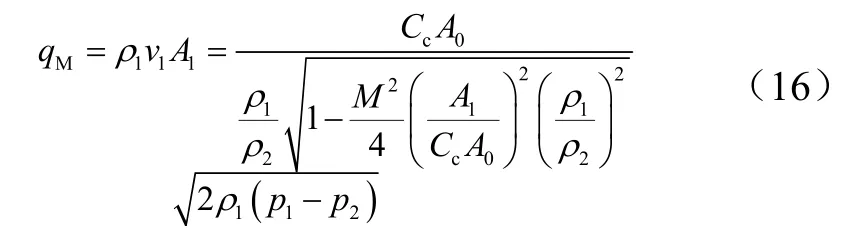
考虑到实际流体的局部能量损失，引入速度系数Cv，且CcCv＝Cd为流量系数[6]，则气液混合流体的节流压差计算公式为

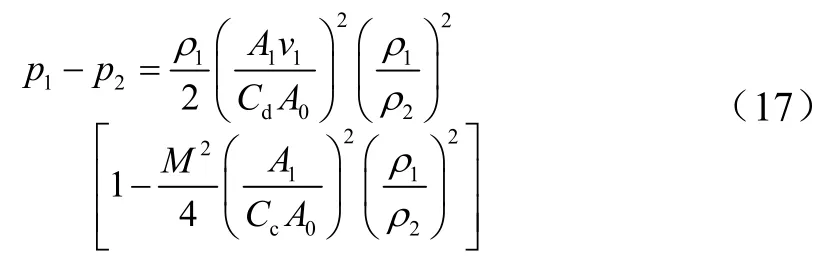
其中，根据式（7）可知：

结合气液两相流体平均密度计算公式[5]，可得气液混合流体在缓冲初始状态时的等效密度ρm0为

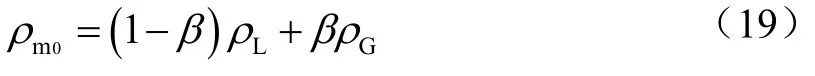
式中：ρL、ρG分别为液体和气体的密度。

由于高速冲击缓冲装置初始准备状态时的压力并非是标准大气压状态，蓄能器需要充气至一定的压力p0，这样在压力为p0时压缩空气密度ρ＝3.482×10-3p/T(kg/m3)，其中，绝对压力p等于表压力p0与标准大气压力之和，T为热力学温度。

结合式（7）可得在压力为p1时气液混合流体密度ρ1的计算公式为

3.2 非隔离式蓄能器气体状态分析

在首次缓冲时，由于蓄能器内气体质量不变，即未发生质量交换，因此根据气体定律可得蓄能器压力：

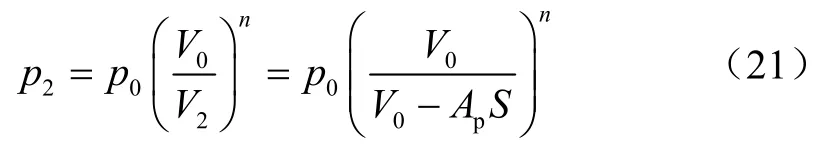
式中：p0为蓄能器初始压力，V0为首次缓冲前蓄能器初始气体体积，Ap为液压缸有杆腔面积；S为液压缸活塞杆位移，n为多变指数，等温过程时n＝1，绝热过程（t≤1 min）时n＝1.4，多变过程一般取n＝1.25[7]。

高速冲击缓冲装置在首次缓冲之后，非隔离式蓄能器上腔大量压缩空气混入到油液中，并随着缓冲装置的复位被带入到液压缸中，使得再次缓冲时蓄能器内的气体有所减少，且随着气液混合程度的加深，滞留在液压缸中的气体量越来越多。根据均相流动模型，若用ΔVmi表示第i次缓冲时蓄能器以外的气液混合流体体积，则此时滞留在蓄能器以外的气体体积为ΔVi＝βΔVmi，故将上式修正如下：

3.3 液压缸压力计算数学模型

用缓冲液压缸有杆腔面积Ap和活塞杆速度v替代式（17）中的A1和v1，根据质量流量连续性方程，气液混合时缓冲液压缸压力的计算公式如下：

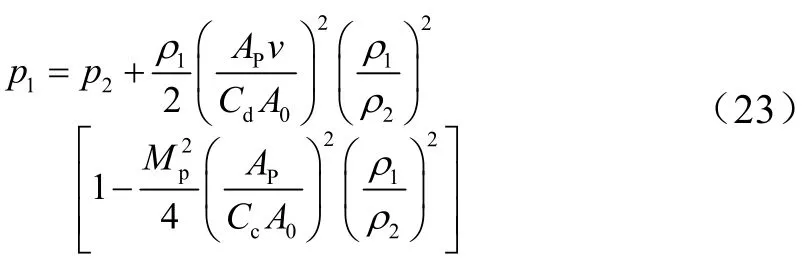
式中：p1为液压缸压力；p2为蓄能器压力；ρ1为气液混合流体密度；A0为流量控制阀节流孔面积；Cd为流量系数；Cc为流束收缩系数；Mp2＝ρ1v2/(γp1)。

4 试验及结果分析

4.1 试验台设计及原理

高速冲击缓冲装置试验台加载装置采用速度和压力复合控制形式，试验台主回路结构简图如图4所示，通过加载液压缸对被试高速冲击缓冲装置缓冲液压缸施加拉力的方式，并利用皮囊式蓄能器的大流量快速响应特点为加载缸提供瞬时能源，从而模拟出高速冲击缓冲装置的高压高速工况。主控回路由高频响插装阀（伺服先导控制、大流量）、比例压力阀和蓄能器组等组成，通过对各类阀件的自动控制以满足试验装置的各项指标。被试高速冲击缓冲装置液压缸内径为210 mm，活塞杆外径为85 mm，液压缸最大行程3.1 m，流量控制阀节流孔径68 mm，蓄能器容积300 L，初始气体体积226 L，液压油采用水乙二醇，初始压力约为5 MPa，缓冲过程最大速度(10±1) m/s。试验台还配备有实时高速监测系统，用于实时监测试验过程中缓冲液压缸压力、速度、行程、蓄能器压力等数据。

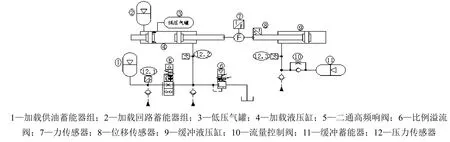
图4 试验台主回路结构简图

4.2 结果分析

试验过程中首次试验前对装置进行排气，随后连续进行20次试验，模拟高速冲击缓冲装置实际工作状态。选取试验中第1、2、5、15次试验数据，将液压缸压力计算数学模型仿真结果与试验结果进行对比，作出液压缸缓冲过程压力变化曲线如图5，作出蓄能器缓冲过程压力变化曲线如图6所示。

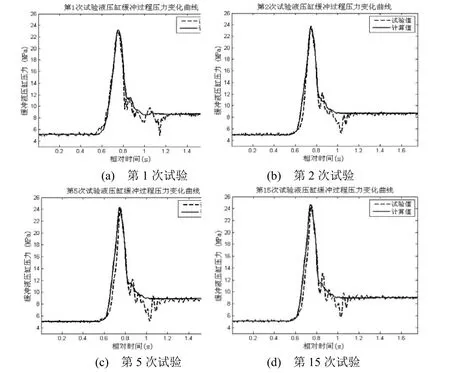
图5 缓冲液压缸压力变化曲线对比

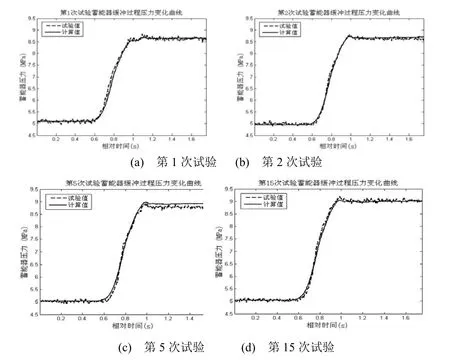
图6 蓄能器压力变化曲线对比

试验过程中，首次缓冲后蓄能器液位急剧升高，而后缓慢升高直至达到气液饱和，表1为压力试验值和仿真计算值对比表，图7为选取的7组试验液压缸缓冲过程压力变化曲线。

表1 压力试验值和仿真计算值对比表

图7 7组试验液压缸压力变化曲线

从图5可看出，液压缸压力模型仿真计算结果与试验结果能够较好地吻合，从图6可看出，在忽略温度对蓄能器压力变化影响的情况下，蓄能器模型仿真结果与试验结果也基本吻合，说明气体混入油液形成的气液混合流体属于可压缩流体范畴。从表1和图7可看出，随着连续试验次数的增加及气液混合程度的加深，液压缸最大压力有明显的升高，说明气液混合形成的可压缩流体使得流量控制阀节流压降增大，是高速冲击缓冲装置在连续使用后压力升高的主要原因。

5 设计改进及验证

5.1 加装进口缓冲器分析

为保持高速冲击缓冲装置多次连续缓冲性能的稳定性和一致性，必须减少油液中气体的混入量，为此在蓄能器瓶口加装了进口缓冲器，如图8所示。在缓冲过程时，高速油液经进口缓冲器的四周流入蓄能器，改变了油液的流动方向，阻止高速油液直接冲入蓄能器上腔的压缩气体中，大大减小了气液混合程度。在复位时，气液混合油液经进口缓冲器后，部分混入油液中的气体被分离出来，使得进入液压管路、流量控制阀和缓冲油缸的油液含气量进一步减少。复位结束后，蓄能器的初始液位只有少许上升，再次缓冲动作后，液压缸压力较前次变化很小。随着缓冲次数的增加，蓄能器中油液的气液混合程度逐渐缓慢加深，直至气液混合达到饱和为止。尽管如此，由于进口缓冲器的作用，缓冲过程中减小了蓄能器部位的气液混合程度，复位过程中又将混入油液中的部分气体分离出来，因而缓冲液压缸、流量控制阀及液压管路中的油液几乎未混入气体，该部位仍可认为是纯油液。

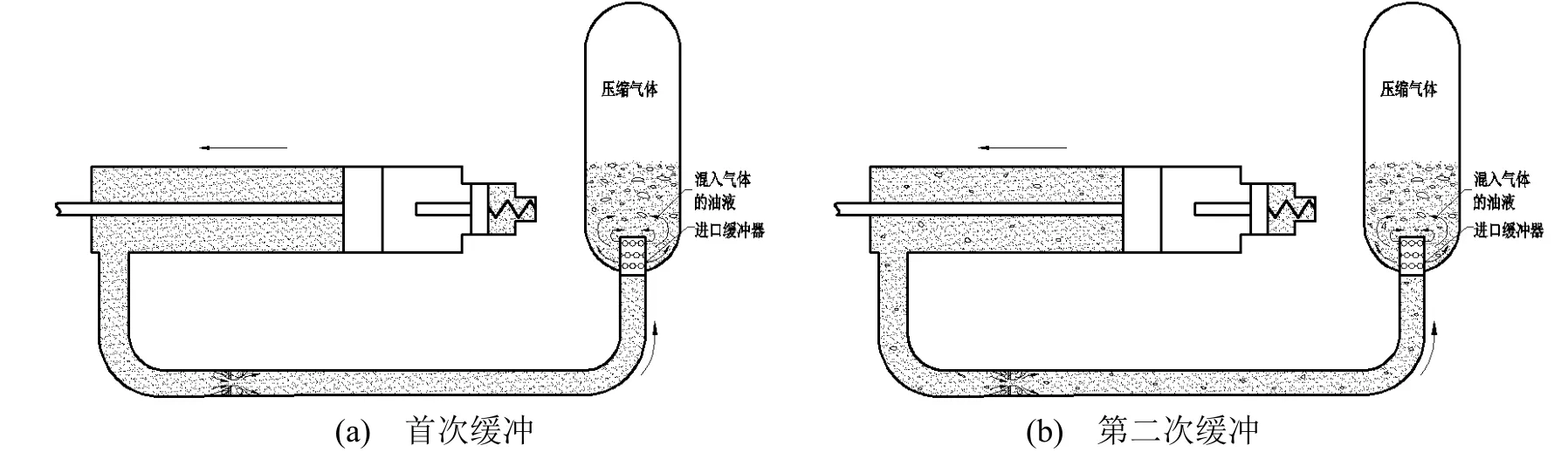
图8 加装进口缓冲器后气液混合示意

5.2 加装进口缓冲器液压缸压力计算模型

蓄能器加装进口缓冲器后，混入缓冲液压缸油液中的气体量大大减少，可认为缓冲液压缸内油液为不可压缩的纯液体，根据不可压缩流体伯努利方程，可得到流量控制阀节流压差Δp为

式中：Δp为节流前后总压降；ρL为油液密度；Cd为流量系数；Ap为液压缸有杆腔面积；A0为流量控制阀节流孔面积；v为活塞杆速度。

在蓄能器加装进口缓冲器后，蓄能器内虽存在气液混合流体，但由于进口缓冲器的气体分离作用，蓄能器气体质量基本保持不变，可用式（22）计算蓄能器压力，故加装进口缓冲器后高速冲击缓冲装置的缓冲过程液压缸压力计算公式为

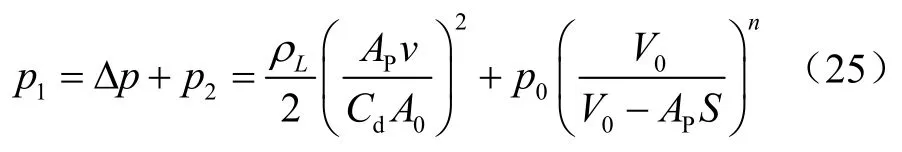
式中：p1为液压缸压力；p2为蓄能器压力；p0为初始压力值。

5.3 试验结果与仿真计算数据对比分析

试验过程中首次试验前对装置进行排气，随后连续进行20次试验，模拟高速冲击缓冲装置实际工作状态。选取试验中第1、2、5、15次试验数据，将加装进口缓冲器后液压缸压力计算数学模型的仿真结果与试验结果进行对比，作出液压缸缓冲过程压力变化曲线如图9所示。

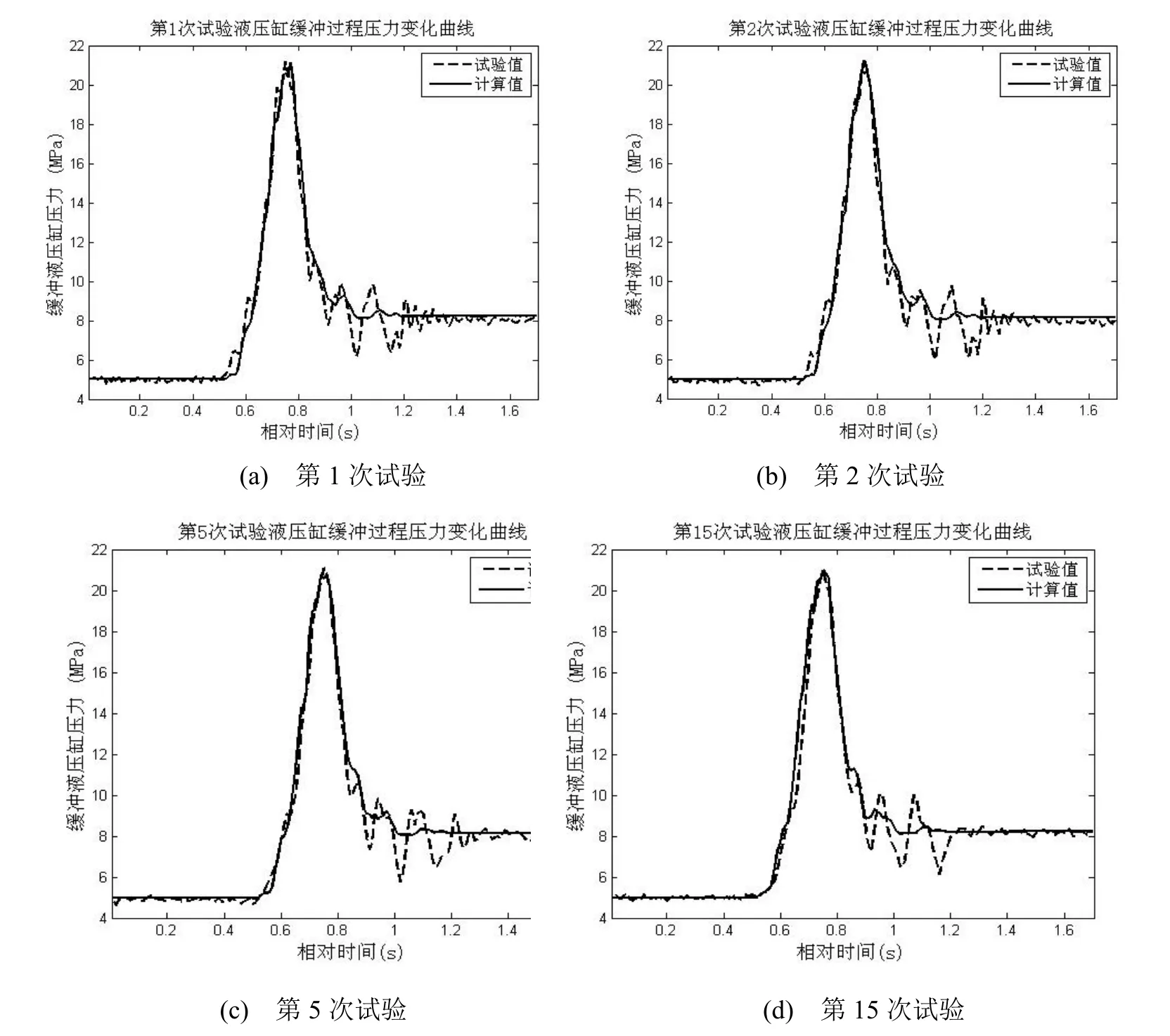
图9 加装缓冲器后液压缸压力变化曲线对比

在加装进口缓冲器后，连续缓冲时蓄能器液位缓慢升高，直至达到气液饱和。试验过程中经过20次缓冲试验后，蓄能器液位升高了70 mm，表2为压力试验值和仿真计算值对比表。

从图9结果来看，液压缸压力模型仿真计算结果与试验结果能够较好地吻合，说明加装进口缓冲器后缓冲液压缸内油液基本是不可压缩的纯液体。从表2可以看出，随着连续试验次数的增加，蓄能器内油液气液的混合程度有所加深，但液压缸最大压力基本保持不变，说明加装进口缓冲器可有效减少非隔离式蓄能器内的气体进入液压缸，形成可压缩的气液混合流体，保证高速冲击缓冲装置多次连续缓冲性能的稳定性。

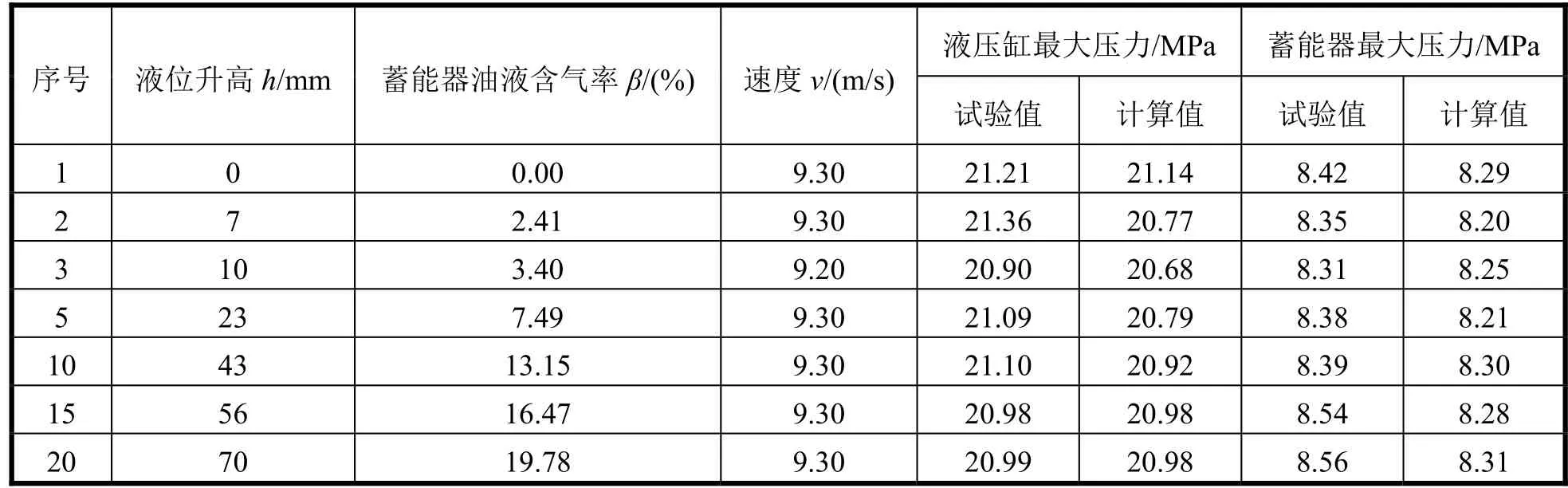
表2 加装缓冲器后压力试验值和仿真计算值对比表

6 结论

本文通过对非隔离式蓄能器气液混合机理的分析，对气液混合流体节流特性进行了深入研究，建立了液压缸压力计算数学模型，并对所建模型进行了试验验证，证明非隔离式蓄能器气液混合形成的可压缩流体，使得流量控制阀节流压降升高，是高速冲击缓冲装置在连续使用后压力升高，进而导致缓冲性能下降的主要原因。此外针对该研究问题，提出加装进口缓冲器以减少非隔离式蓄能器气液混合的解决方案，并通过试验验证了该解决方案可有效减少非隔离式蓄能器内的气体进入液压缸形成气液混合流体，避免高速冲击缓冲装置在连续使用过程中压力显著升高，保证其多次连续缓冲性能的稳定性。