推挽式谐振加速度传感器设计及仿真研究*
都捷豪, 石云波, 李 飞, 赵 锐, 曹慧亮, 刘翔天
(中北大学 电子测试技术国防科技重点实验室,山西 太原 030051)
0 引 言
硅微谐振式加速度计可以将外界的加速度信号转变为频率信号进行输出,具有体积小、精度高、价格低、易于生产等特点。随着传统行业如汽车、航天和武器制导等行业需求越来越大,并伴随着手机、玩具、可穿戴设备在内的消费电子产品迅速崛起,对硅微谐振式加速度计性能有了更高的要求。其中,美国Draper实验室采用了差分输出的谐振式加速度计,谐振频率达到20 kHz,有效灵敏度为100 Hz/gn[1,2]。伯克利分校提及了一种应用于地震监测的微机电系统(micro-electro-mechanical system,MEMS)谐振式加速度样机,其特点是在质量块和双端固定音叉之间加入了杠杆机构,放大了质量块的惯性力,最终使灵敏度提高至160 Hz/gn[3]。南京理工大学苏岩教授通过两级杠杆放大结构和差分输出的双端固定音叉(double-ended tuning forks,DETF)谐振器,设计出样机尺寸约为45 mm×30 mm×20 mm的加速度计,零偏不稳定度达到1 μgn,分辨率为2.5 μgn/Hz[4]。清华大学通过对结构的优化和测试电路补偿技术,减少环境温度变化导致的谐振频率的变化。使零偏稳定性降低到10 μgn[5]。为了提升加速度计的灵敏度和精确度,从而提出本文所设计结构。
本文采用微杠杆和双端固定音叉差动输出的方式设计了一种新型的单轴推挽式谐振加速度传感器,提高了谐振式加速度传感器的输出灵敏度,解决了两个独立谐振器受力不同的问题。
1 工作原理与结构设计
1.1 工作原理
推挽式谐振加速度计在工作时将加速度信号转换成谐振器的谐振频率,通过测量谐振梁频率的变化量从而得到载体的加速度[6]。测试时,质量块在加速度作用下产生惯性力,惯性力经杠杆机构放大后传递到两个DETF谐振器上,一个受轴向拉力导致谐振频率增加,另一个受轴向压力导致谐振频率下降,经过信号的差分输出得到它们的频差。在一定加速度范围内,其值与输入加速度值呈线性关系。
通过将谐振梁振动模型视为欧拉伯努利模型,忽略非线性项,可以得到梁的振动方程为[7]
(1)
其中
(2)
式中E为低阻硅的杨氏模量;F为谐振梁受到轴向力;f0为谐振器在没有受到轴向作用力时的谐振频率;ρ为低阻硅的密度;w,l和t分别为谐振梁的宽、长和厚。因此,两差分输出的谐振器的频率差值为
Δf=f1-f2
(3)
在忽略DETF谐振器梁的弯曲挠度时,谐振梁受到的轴向应力和轴向应变关系可以近似为
F=wt·σ
(4)
因此,根据上述公式可以得出
(5)
1.2 结构设计和优化
本文设计一种推挽式MEMS谐振加速度计结构如图1所示,整个结构由固定锚点、折叠梁、质量块、杠杆机构,连接梁和双端固定音叉构成,呈中心对称。设计差分输出的两谐振器通过它们之间的连接梁连接,质量块的作用力通过两组对称的杠杆放大机构实现对连接梁的推挽,将作用力传递到两谐振器上。通过这一设计,两谐振器受到的惯性力都是来自于连接梁,此时两谐振器受到的力大小相同,分别受到压力和拉力。实现了对两谐振器的全差动输入,进而保证差分输出的一致性。

图1 推挽式MEMS谐振加速度计结构示意
对所设计结构进行尺寸优化,目的在于提高结构的灵敏度,增大工作模态和干扰模态的频差。本文利用Ansys对加速度计的结构进行优化。通过对连接梁长度及宽度进行有限元仿真分析,发现连接梁的长度和宽度对灵敏度和谐振器模态频差的影响较为明显。如图2(a)所示,随着谐振梁长度的增加到1 500 μm,灵敏度达到相对稳定,并且谐振器模态频差也随长度增加达到稳定。本文将连接梁的长度设计为1 600 μm,保证谐振式加速度计灵敏度的稳定性增大,谐振器工作模态和干扰模态的频差达到最大值1 473 Hz。
连接梁宽度对灵敏度和频差的影响如图2(b)所示。通过仿真发现灵敏度随着连接梁的宽度变化状况,当宽度达到800 μm时,灵敏度达到210 Hz/gn,谐振器的工作模态与干扰模态的频差也随之增加,可以设计连接梁最佳宽度为800 μm。
通过对谐振器梁间距进行有限元分析,找出谐振器两个模态频差最大的尺寸。谐振梁间距与谐振器工作模态频率以及工作模态与干扰模态频差的变化规律如图2(c)所示。可以看出在改变间距时,谐振频率变化不明显。在间距为40 μm时,频差最大,故本文选择间距为40 μm。
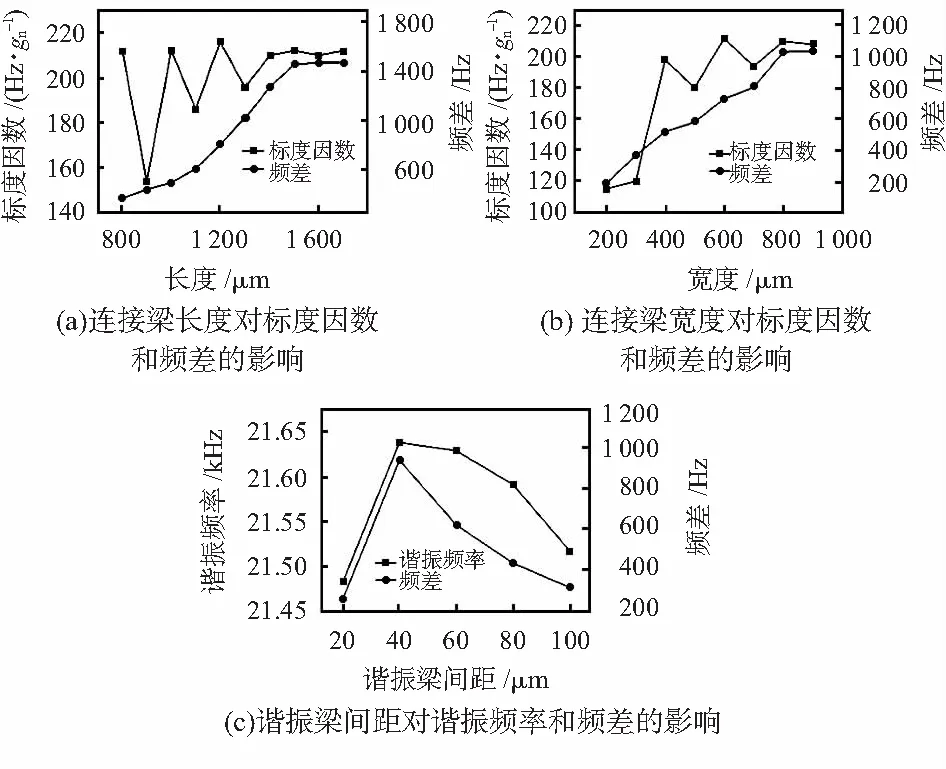
图2 谐振梁长度、宽度、间距对谐振频率和频差的影响
其余关键结构参数如表1所示。

表1 部分关键结构参数
2 仿真分析
2.1 模态仿真
根据图1所示的结构方案,建立仿真模型验证推挽式谐振加速度计的工作原理,利用Ansys仿真软件对其进行有限元模型优化。为了提取加速度计谐振器的工作模态如图3所示,通过Ansys对谐振式加速度计进行模态仿真,提取谐振器的高阶模态直至仿真出谐振器呈工作模态的振型,仿真得到的第23阶和第24阶模态的振型为谐振器的工作模态,谐振器谐振的频率值为21.708,21.715 kHz。

图3 谐振器的工作模态
由于仿真的误差使得两对称谐振器的谐振频率存在一定的误差,通过对比仿真结果均值与理论计算的结果的相对误差为2.6 %,并且仿真得出了双端固定音叉的其它不同模态,确定其它干扰模态与工作模态的频差,仿真得出谐振器的同向模态即干扰模态为20.532 kHz,如图4所示。通过计算工作模态频率的均值与干扰模态频率的差值为1.179 5 kHz。结果表明,工作模态与其他干扰模态频差明显,有效实现了隔离,证明了此推挽式谐振加速度传感器的可行性。

图4 谐振器的干扰模态
2.2 静力灵敏度仿真
通过静力学仿真给加速度计在敏感轴方向施加不同的加速度,再结合模态仿真得出两谐振器在工作模态时的谐振频率[7,8]。通过比较施加加速度前后谐振器谐振频率的增量和减量,通过差分计算频率变化量可以得出加速度与频率变化量的关系如图5所示。可以看出谐振式加速度计谐振器的谐振频率在一定范围内与加速度呈线性关系,加速度计在±5gn的灵敏度为280 Hz/gn。

图5 频率变化量和加速度的关系
通过在非敏感轴方向施加不同的加速度仿真出两谐振器的频率变化量,得出频率变化量与横向加速度的关系[7]。即X轴方向和Z轴方向加速度对谐振器频率变化的影响,仿真结果如图6所示的关系。可以看出此加速度计在X轴方向上在10gn范围内谐振频率的变化量为0.4 Hz/gn,在Z轴方向上在10gn范围内谐振频率的变化量为0.1 Hz/gn,因此可以得出加速度计在非敏感方向在一定范围内的加速度对谐振器谐振频率的影响微弱。说明该结构可以很好地避免横向加速度对传感器输出的影响。
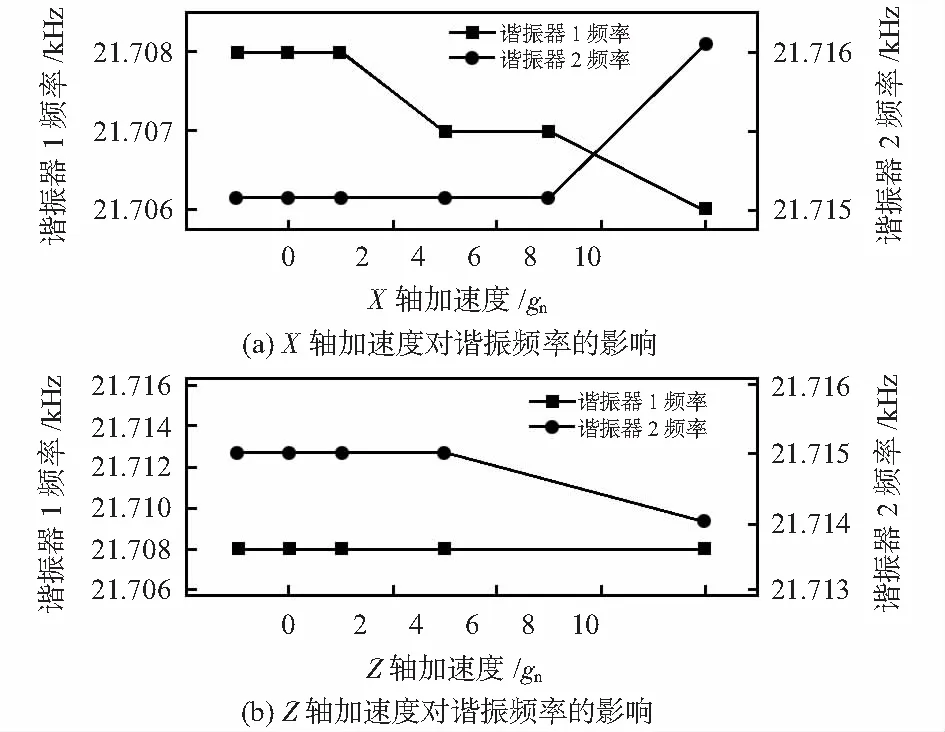
图6 非敏感方向对谐振频率的影响
2.3 谐响应仿真
通过谐响应分析在谐振梁上施加不同驱动力,得出谐振梁上驱动位移,由于施加的驱动力进行了扫频分析,对于同一驱动力在频率达到谐振梁的谐振频率时,谐振梁的驱动位移达到最大值。仿真求解得出了谐振梁在一定Q值不同驱动力的作用下的驱动位移和相位关系。图7反映了在Q值为10 000时谐振梁的振幅与相位在不同驱动力作用下的变化曲线。对比不同驱动力作用下,驱动力增大,谐振梁的振幅也随之增大。

图7 Q=10 000时谐振梁在不同驱动力作用下的幅值与相位
图8反映了在不同Q值条件下谐振梁最大振幅与驱动力的关系,可以得出在同一驱动力作用下谐振梁在其谐振频率点振幅急剧增大,远大于其它频率点,其谐振器谐振频率的响应点为21.716 kHz。通过数据处理发现谐振梁的振幅与驱动力的大小成正比,并且随着Q值越大,谐振器振幅越大。驱动力与驱动电压的关系为驱动电路的设计提供仿真依据。

图8 不同Q值条件下最大振幅与驱动力的关系
3 闭环驱动系统仿真
对推挽式谐振加速度计中DETF谐振器采用MATLAB中的SIMULINK软件进行闭环驱动回路仿真,可以通过自激振荡的方式来实现系统闭环[9,10]。当系统满足式(6)所示幅值和相角条件时,整个闭环系统就能形成稳定的自激振荡
|A(jω)·H(jω)|ω=ω1=1;
arg(A(jω)·H(jω))=0+k·2π,k=0,1,2…
(6)
加速度计闭环控制实现幅值闭环和相位闭环两个闭环回路,加速度计的控制目标是谐振频率的准确性和稳定性。通过构造系统闭环来保证谐振音叉的动态特性和力学特性,保持系统稳定工作。本文所设计自激振荡闭环驱动SIMULINK模型图如图9所示。

图9 加速度计自激振荡闭环系统SIMULINK模型
SIMULINK模型框图主要包括两个闭环。首先,是由前置的C/V转换放大器和90°移相模块构成,来满足自激振荡的相角条件。其次,通过整流器、低通滤波器以及PI控制器构成稳幅控制回路,满足所需幅值条件。
对此闭环系统进行仿真,仿真结果如图10所示。其中图10(a)表示此加速度计机械模型在闭环控制中谐振器振动幅度为0.1 μm,谐振器可在其振幅下可以进行线性振动;同时为系统闭环工作所需驱动电压为1 V左右,满足驱动要求。图10(b)为PI控制前后曲线,上图可以看出系统在0.2 s左右达到稳定控制,下图PI控制后的输出波形系统频率稳定时间为0.01 s左右,较无PI控制时间有了大幅提升。通过上述仿真说明加速度计可以在此闭环系统下正常工作,也再次验证了结构设计的合理性。

图10 自激振荡闭环控制仿真
4 结 论
本文提出了一种新型单轴推挽式MEMS谐振加速度计,主要研究了其微杠杆、DETF等的工作原理,并对其中的连接梁、谐振器进行了结构参数优化。结合相关的参数对其进行了模态、静力和谐响应分析。模态分析结果表明DETF工作模态(21.708 kHz和21.715 kHz)与干扰模态(20.532 kHz)保持了1.179 5 kHz的频差,保证结构可以正常工作;静力分析其在敏感轴的灵敏度为280 Hz/gn,非敏感轴方向的灵敏度分别为0.4 Hz/gn和0.1 Hz/gn;谐响应分析谐振结构可以很好地工作在谐振频率点上,并且分析了Q值对谐振器振幅的影响。最后通过搭建自激振荡闭环驱动系统,验证结构可行性。上述结果对提出推挽式MEMS谐振加速度计提供了理论依据。

