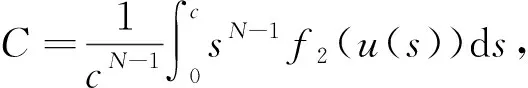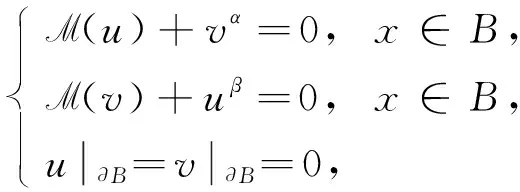Minkowski空间中含平均曲率算子的拟线性微分系统Dirichlet问题径向正解的唯一性
苗亮英, 何志乾
(1. 青海民族大学 数学与统计学院, 西宁 810007; 2. 青海大学 基础部, 西宁 810016)
0 引 言
Minkowski空间中给定平均曲率方程在微分几何和广义相对论中应用广泛, 例如相对论状态下的质点运动状态研究[1]及非线性电动力学理论中的Born-Infeld模型[2-3]等. 目前, 关于其正解的存在性和多解性研究已取得了丰富成果[4-13], 其中Coelho等[4]研究了一维Minkowski空间给定平均曲率型方程Dirichlet问题
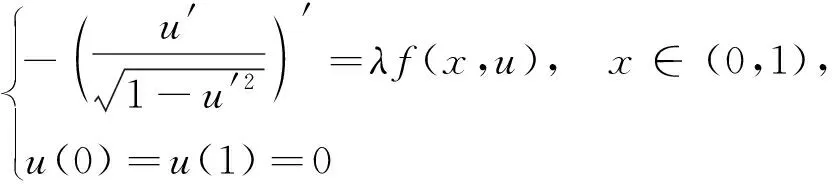
(1)
正解的存在性和多解性, 用变分法和拓扑度方法得到了问题(1)至少存在1个、 2个、 3个正解的存在性, 其中f是一个Lp-Carathéodory函数.Gurban等[5]研究了两参数问题
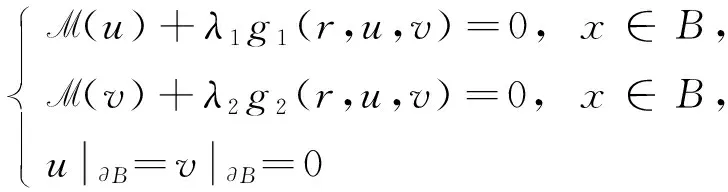
(2)
径向正解的存在性, 用锥上的不动点理论, 得到了如下结果:
定理1[5]假设gi: [0,1]×[0,∞)2→[0,∞)是连续的, 关于变元s,t拟单调非减并满足对任意的r∈(0,1], 有
g1(r,s,t)>0,g2(r,s,t)>0, ∀s,t>0;g1(r,ξ,0)=g2(r,0,ξ)=0, ∀ξ>0,

文献[6-7]用分歧理论和Leggett-Williams不动点定理分别研究了问题(2)径向正解的全局结构以及至少存在3个甚至无穷多个径向正解的存在性. 但关于含平均曲率算子的拟线性微分系统Dirichlet问题径向正解的唯一性研究目前尚未见文献报道. 受上述研究启发, 本文考虑含平均曲率算子的拟线性微分系统Dirichlet问题
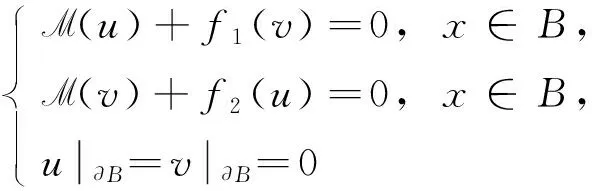
(3)
径向正解的唯一性, 其中fi∈C([0,∞),[0,∞)),i=1,2,B为N(N≥2)空间中的单位球.
本文总假设:
(H1)fi: [0,∞)→[0,∞)是连续函数且fi(i=1,2)不恒为零.
1 预备知识
考虑问题(3)径向正解的存在性, 令r=|x|, 则u(|x|)=u(r),v(|x|)=v(r), 问题(3)退化为如下混合型边值问题:

(4)


引理1[14]对任意的u∈C([0,1],[0,∞))满足当r∈[0,1] 时,u′(r)是递减的, 则


φ-1(s1)φ-1(s2)≤φ-1(s1s2)≤s1s2, ∀s1,s2∈[0,∞).
特别地, 当0 定义P是C中的锥, 其中P={u∈C[0,1]:u(t)≥0,t∈[0,1]}.定义PR={u∈P: ‖u‖ (5) (6) 由文献[9]可知, 每个解算子Ti(i=1,2)都是非负上凸函数, 结合引理1可知Ti:P→P是全连续算子.定义复合算子T(u)=T1∘T2(u), 则由T的定义可知T(u):P→P也为全连续算子.由式(5),(6)可知(v1,v2)∈C1[0,1]×C1[0,1]是问题(4)的解当且仅当v1=T1v2,v2=T2v1, 其中(v1,v2)∈P{θ}×P{θ}. 1) 若‖Tx‖≥‖x‖,x∈∂Kr, 则i(T,Kr,K)=0; 2) 若‖Tx‖≤‖x‖,x∈∂Kr, 则i(T,Kr,K)=1. 定义1[15]令K为实Banach空间Y中的锥.令A:K→K且u0>θ, 其中θ表示Y中的零元素. 1) 对任意的x>θ, 存在θ1,θ2>0, 使得θ1u0≤A(x)≤θ2u0; 2) 对任意的αu0≤x≤βu0且t∈(0,1), 存在某些η>0, 使得A(tx)≥(1+η)tAx. 则A称为u0-次线性算子. 引理4[15]一个递增的u0-次线性算子T最多有一个正的不动点. 定理2假设(H1)成立且fi递增, 使得对任意的u>0,t∈(0,1), 存在某些η>0, 使得 fi(tu)≥(1+η)tfi(u),i=1,2. 则问题(3)存在唯一的径向正解. 证明: 由T1和T2的定义可知,T1和T2都是P诱导的递增算子.令T=T1∘T2, 则为得到问题(3)径向正解的唯一性, 只需证明T在P中最多有一个不动点.由引理4, 只需验证在C[0,1]空间中, 对某些u0>0,T:P→P是u0-次线性的. 令u0=1-r,r∈[0,1]且θ2=M/N, 则T2(u)(r)≤θ2u0. T2(u)(r)≥T2u(c)≥Γ3(1-c),r∈[0,c]. 其次, 证明对任意的θ1u0≤x≤θ2u0且ξ∈(0,1), 存在某些η>0, 使得 T(ξu)≥(1+η)ξTu. 由T1和T2的定义, 易得 同理可得T1(ξu)≥(1+η)ξ(T1u)(r).即 T(ξu)≥T1∘((1+η)ξT2(u))≥(1+η)2ξT1∘T2(u)≥(1+η)ξTu, 表明T满足定义1中2), 从而T是u0-次线性的, 由引理4可知,T在P中最多有一个不动点.因此, 问题(3)至多存在一个径向正解.特别地, 在文献[7]中利用引理1和引理3, 可证明问题(3)至少存在一个径向正解, 故问题(3)恰好存在一个径向正解.证毕. 例1考虑如下边值问题: (7) 其中0<α,β<1.显然, 问题(7)的非线性项满足定理2的所有条件, 由定理2可知问题(7)恰好存在一个径向正解.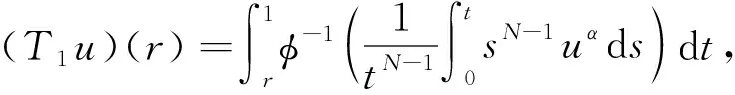
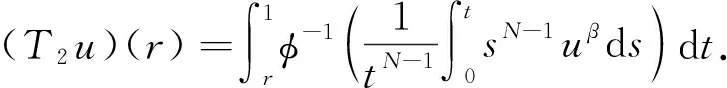

2 主要结果