一类Poisson-Nernst-Planck方程的边平均有限元计算

倪宇晖, 阳 莺

(桂林电子科技大学 数学与计算科学学院, 广西高校数据分析与计算重点实验室, 广西密码学与信息安全重点实验室， 广西 桂林 541004)

本文考虑一类Poisson-Nernst-Planck(PNP)数学模型, 它是由Nernst-Planck(NP)方程和Poisson方程耦合而成. PNP方程组在半导体[1]和生物分子[2]等领域应用广泛. 例如, 在半导体领域中, 半导体器件中的电流通常由电子和空穴两类载流子移动产生, PNP模型用于描述半导体载流子的运动规律, 通过计算方程可得到半导体内的电势分布和载流子浓度分布.

由于PNP模型是一个强耦合、 强非线性的偏微分方程组, 所以仅在极少数情形下能找到它的解析解. Gummel[3]首次用数值方法代替解析方法讨论了一维双极晶体管的电学性质, 从而开启了计算机数值模拟半导体器件的时代. 基于半导体器件复杂的空间结构和边界条件, 善于构造高精度格式的有限元方法[4]和满足流守恒的有限体积法[5]在实际应用中被广泛应用.

基于半导体的电学性质, PNP方程常有对流占优的特点, 而利用标准有限元方法对对流占优问题进行求解时易出现伪振荡. 对于一般的对流占优问题, 目前已有一些特殊的有限元方法, 例如Petrov-Galerkin有限元法[6]、 流线扩散有限元法[7]以及边平均有限元方法[8]等. 边平均有限元方法是一类迎风有限元方法, 其能自动选择迎风方向, 用该方法可使离散所得的刚度矩阵是M-矩阵. 本文针对半导体中的一类PNP方程构造一种边平均有限元离散形式. 在合适的网格假设下, 离散所得的总刚度矩阵是M-矩阵. 将边平均有限元的数值结果和标准有限元进行对比, 得出边平均有限元方法在求解这一类PNP方程所需时间仅为标准有限元的40%, 且计算出的解误差略低.

1 预备知识

设Ω是3中的有界区域, 满足Lipchitz连续, ∂Ω表示边界.本文用H1(Ω)表示一阶导数属于L2的函数构成的Soblev空间,C0(Ω)表示区域上的连续函数空间.Γh表示区域Ω分解的单元集合,T∈Γh表示四面体单元.Nh表示节点总数, 用xi(i=1,2,…,Nh)表示区域Ω内的所有节点, 用qi(i=1,2,3,4)表示单元T上的节点,E表示边,Eij表示以qi为起点、 以qj为终点的边.

考虑一类在半导体领域中的稳态PNP方程[9]：

方程(1)为Poisson方程, 描述了静电势与空穴、 电子浓度分布的关系, 在半导体领域称为电势方程. 方程(2),(3)为NP方程, 描述了空穴和电子两种载流子的运动规律, 又称为载流子连续性方程. 方程的边界为Dirichlet边界条件：

其中ud,pd,nd是与位置坐标相关的已知函数.

2 边平均有限元的离散形式

首先在线性有限元空间Vh上定义一组基函数φi(i=1,2,…,Nh), 它们均在区域Ω内连续, 在每个单元内是线性函数, 且

φi(xi)=1,φi(xj)=0,j≠i.

(4)

2.1 Poisson方程的离散形式

迭代计算中,p和n会用上一步求解得出的值或为给定初值, 所以方程(1)会变成Poisson方程的形式.下面给出边平均有限元离散步骤[8].

(5)

针对任意有限元空间的函数Φ定义记号δE为

δEΦ=Φ(qi)-Φ(qj).

(6)

基于式(5)的结果, 可得Poisson方程的边平均有限元的离散形式:

(7)

(8)

引理1[8]Poisson方程边平均有限元的离散形式对应的总刚度矩阵是M-矩阵, 当且仅当对所有边E, 下列等式均成立:

(9)

这里,T⊃E表示包含边E的所有单元T.

2.2 NP方程的离散形式

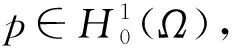
其中

首先定义J(p), 函数ψE和e-ψE在边E上的调和平均αE如下:

J(p)=p+pu,

(10)

(11)

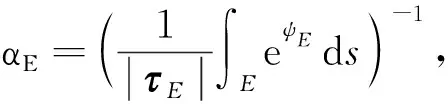
(12)

(13)

这里,δE由式(6)定义.

如果将J(p)在单元T上视为一个常向量JT(p), 则由式(12)和式(13)可推出

JT(p)·τE≈αEδE(eψEp).

(14)

利用式(7)和式(8)可知, 对任意的vh∈Vh, 均有

(15)

将式(10)和式(14)代入式(15), 可得在单元上满足

(16)

式(16)右端的ψE与u有关.利用式(16)可得

(17)

(18)

因此可得方程(2)的边平均有限元离散形式: 寻找ph∈Vh, 满足

ah(ph,vh)=f(vh),vh∈Vh.

(19)

引理2[8]NP方程的有限元离散形式(19)对应的总刚度矩阵是M-矩阵的充分必要条件是式(9)成立.

由引理1和引理2可见, 当式(9)成立时, PNP方程的总刚度矩阵均为M-矩阵, 使求解过程变得更稳定.

2.3 边平均有限元的实际计算

当Vh是线性有限元空间时,uh在每个单元上是常数, 此时式(18)可进一步简化.下面讨论ah(ph,φi), 首先将φi代入式(18)并利用基函数的特性(4), 可得

(20)

在实际计算中, 式(20)中αEeψE(xi)和αEeψE(xj)的计算较复杂, 所以本文针对这两项做进一步处理.如果x是边E上的一点, 则该点必能表示为x=s(xi-xj)+xj(0≤s≤1), 根据式(11)的定义有

这里τE=qi-qj.因此

(21)

对式(21)沿边E积分, 并利用微分学基本定理, 可得

这里B(s)是一个Bernoulli函数, 定义为

αEeψE(xj)=B(uh·τE).

(22)

由式(22)可推出

αEeψE(xi)=B(-u·τE).

(23)

将式(22)和式(23)代入式(19), 可得方便计算的边平均有限元离散形式: 寻找ph∈Vh, 使得对∀φi(i=1,2,…,Nh), 满足

ah(ph,φi)=f(φi),

这里,

2.4 数值实验

为验证边平均有限元方法在PNP方程计算中的有效性, 本文选取一个有真解的数值算例, 并与标准有限元方法进行比较. 实验环境为个人电脑, CPU为2.10 GHz, 内存为32 GB, 在电脑上运行MATLAB 2018b软件.

计算区域Ω=[-1/2,1/2]3是边长为1 nm的正方体区域, 边界∂Ω为正方体的6个面. 网格内所有单元的二面角均小于等于90°, 所以采取的网格剖分满足总刚度矩阵为M-矩阵的充分必要条件(9), 如图1所示.

图1 四面体网格剖分Fig.1 Tetrahedral mesh division

这里,cbulk是为模型真解设定的浓度, 此处取为6.022×1026m-3, 即10-3mol/L.将各物理参数值和单位代入并无量纲化后可见, 真解pr和nr的值非常大, 达到1025数量级, 由于计算机的精度限制, 该值可能对结果有影响, 因此本文做如下系数规范化：

进行系数规范后可得新的方程组：

这里cλ=0.179 07, 边界条件和真解为

显然, 求出该方程即可得原问题的解.在不同的自由度下, 本文分别使用边平均有限元方法和标准有限元方法对该方程进行求解, 结果分别列于表1和表2.

表1 精确解与边平均有限元解的L2模误差

表2 精确解与有限元解的L2模误差

由表1和表2可见, 在自由度相同的情形下, 边平均有限元方法所用的CPU时间约是有限元方法的40%.

综上, 本文给出了半导体器件中一类PNP方程的边平均有限元离散形式, 该离散形式下的总刚度矩阵为M-矩阵. 数值实验结果表明, 边平均有限元方法得出的解在误差上略小于标准有限元法, 且CPU时间更短.

感谢中国科学院数学与系统科学研究院张倩茹在数值实验方面提供的帮助.