基于3×3高维核矩阵的终止极化码研究

文 豪，曹 阳

重庆理工大学电气与电子工程学院，重庆400054

极化码是一种理论上证明在离散无记忆信道中可以达到信道容量的编码方案，并且其编译码复杂度较低[1]。传统极化码是基于2×2 核矩阵构造的，其码长只能为2n，研究表明由l×l(l＞2)生成核矩阵构造的极化码有望实现更好的纠错性能[2-3]。文献[4-5]表明：极化核矩阵要满足矩阵可逆且置换后非上三角矩阵，同时给出极化码的渐进性能为PE(N)＜2-lnE(G)，其中E(G) 为矩阵G的极化率。文献[6]进一步研究不同3×3 极化核矩阵编译码的复杂度。文献[7-8]利用RS 码、代数几何编码作极化核矩阵，进一步提高了极化码的渐进性能。文献[9]提出归一化极化距离的概念，分析不同核矩阵下的极化码性能，并给出3×3 与4×4 核矩阵构造极化码的误块率（block error rate,BLER）上界。上述文献表明只要满足相应的约束条件，高维核矩阵也可作为极化码的编码生成矩阵，但会造成更高的计算复杂度和译码延迟。

针对极化码的高计算复杂度和译码延迟问题，专家与学者对极化码的构造进行了以下研究：文献[1]提出以巴氏参数的方法递归构造极化码，通过提出巴氏参数来衡量比特信道质量；文献[10]引入密度进化法（density evolution,DE）计算极化后每个比特信道的错误传输概率，继而确定其比特信道的可靠性；文献[11]引入高斯近似法（Gaussian approximation,GA）进而通过估计近似值来降低密度演进方法的计算复杂度。文献[12]将高斯近似与蒙特卡罗相结合，提出一种基于蒙特卡罗的两阶段极化码构造方法。文献[13]将通用偏序应用于大气弱湍流信道中，提出一种适用于大气弱湍流信道的低编码复杂度的构造法。虽然上述极化码构造方法优势明显，但对计算复杂度的降低还有一定的提升空间。文献[14-15]引入终止极化的思想，终止极化是当信道极化到一定程度后部分信道已经足够好或非常差，于是停止该部分信道继续极化的操作，其计算复杂度能减少19.4%～23.7%，但其理论证明仅限于2×2 核矩阵。

本文针对高维核矩阵构造的极化码以计算复杂度换取纠错性能的问题，将终止极化思想应用于高维核矩阵构造的极化码，提出基于3×3 高维核矩阵终止极化码的构造方案。不同于2×2 核矩阵只有一种形式，3×3 核矩阵具有多种形式，本文首先基于文献[16]将3×3 核矩阵进行分类，以此表示出不同核矩阵巴氏参数公式的形式；再针对不同3×3 核矩阵构造的终止极化码性能可能不同的问题，列出满足信道极化条件的所有3×3 核矩阵及其极化率，以具有最高极化率核矩阵G531进行终止极化码的构造，理论证明其纠错性能优于传统完全极化码；最后在二进制擦除信道（binary erasure channel,BEC）上推导出G531终止极化码复杂度降低比（complexity reduction ratio,CRR）的上下界，并验证了其合理性，在保证3×3 高维核矩阵极化码的误码率性能的同时又保证其计算复杂度较低。

1 极化码构造原理

1.1 信道极化

极化码是基于信道极化的，信道极化包括信道组合及信道分裂。将信道W复制N次形成N条独立同分布信道，N条信道经过信道组合形成合成信道WN，再将WN进行信道分裂得到N条具有前后依赖关系的子信道，子信道i表示为WiN。经过以上极化操作，一部分子信道信道容量I(W) 趋为1，这部分信道称为好信道，表示为GN(W,β)，用来传输载有有用信息的比特位；另一部分子信道信道容量趋为0，这部分信道称为差信道，表示为BN(W,β)，用来传输收发双发都已知的冻结位，其中β为正常数，且满足β＜1/2。X和Y分别表示二元离散无记忆信道的输入输出符号集，X={0,1}，若信道为BEC，则Y={0,q,1}，其中q为擦除概率。为了构造极化码，需要对巴氏参数Z(W) 进行信息位的选取

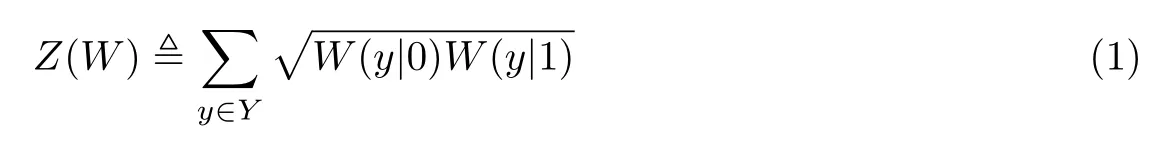
式中：Z(W) 用来衡量子信道的可靠性，Z(W) 越大表示子信道的可靠性越低。W(y|x) 为信道的转移概率，且x ∈X,y ∈Y。

二元无记忆对称（binary memoryless symmetric,BMS）信道，信道W的错误概率为

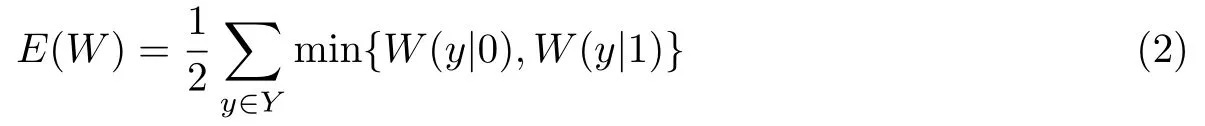
BMS 信道错误概率上界与巴氏参数需满足以下条件[16]

在进行极化码信息位选取时，选取巴氏参数小或错误概率低的好信道进行信息传输。好信道集合表示为

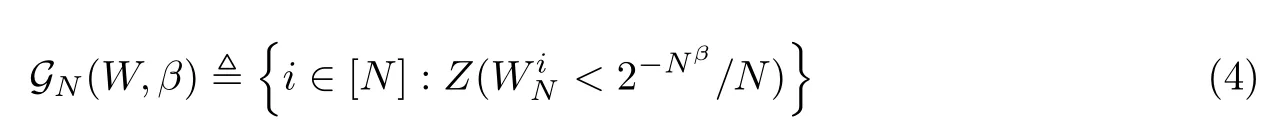
当常数β＜1/2 时，BMS 信道中的W满足

即当码长足够大时，信息传输速率能达到信道容量，实现无错传输。

1.2 3×3 核矩阵的巴氏参数

3×3 核矩阵的构造形式多样，列出每个核矩阵对应的巴氏参数公式太过赘述，因此首先对G3进行分类，再给出每类的巴氏参数计算公式。

当G3核矩阵最后一行“1”的个数为1，即m=1 时，满足信道极化的3×3 核矩阵Gm=1有4 种形式[5]，其巴氏参数为

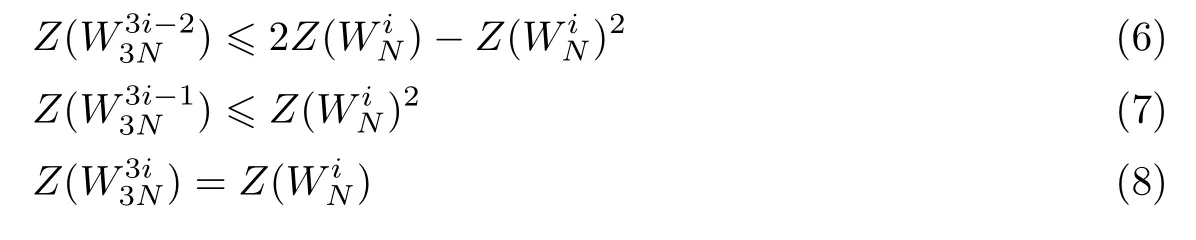
当m=2 时，满足信道极化的核矩阵有9 种。这9 种核矩阵的巴氏参数有两种形式：一种为Gm=2，其巴氏参数公式与Gm=1相同；另一种巴氏参数为

当m=3 时，满足信道极化的核矩阵Gm=3有4 种[5]，其巴氏参数为

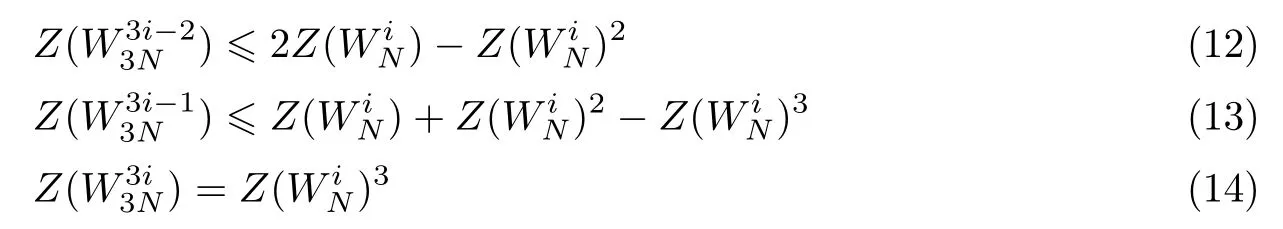
若信道为BEC 信道，则式(14) 等号成立。3×3 核矩阵形式不唯一，其极化率也不同，根据文献[3]所述，3×3 矩阵核的极化率可表示为

式中：Di为核矩阵的部分距离。Gabc为某一核矩阵，Eabc(G) 为对应核矩阵的极化率，a、b、c分别为核矩阵第1、2、3 列的十进制表示形式。例如极化率为0 的G421=表示为E421(G)。不同核矩阵极化率如表1所示。

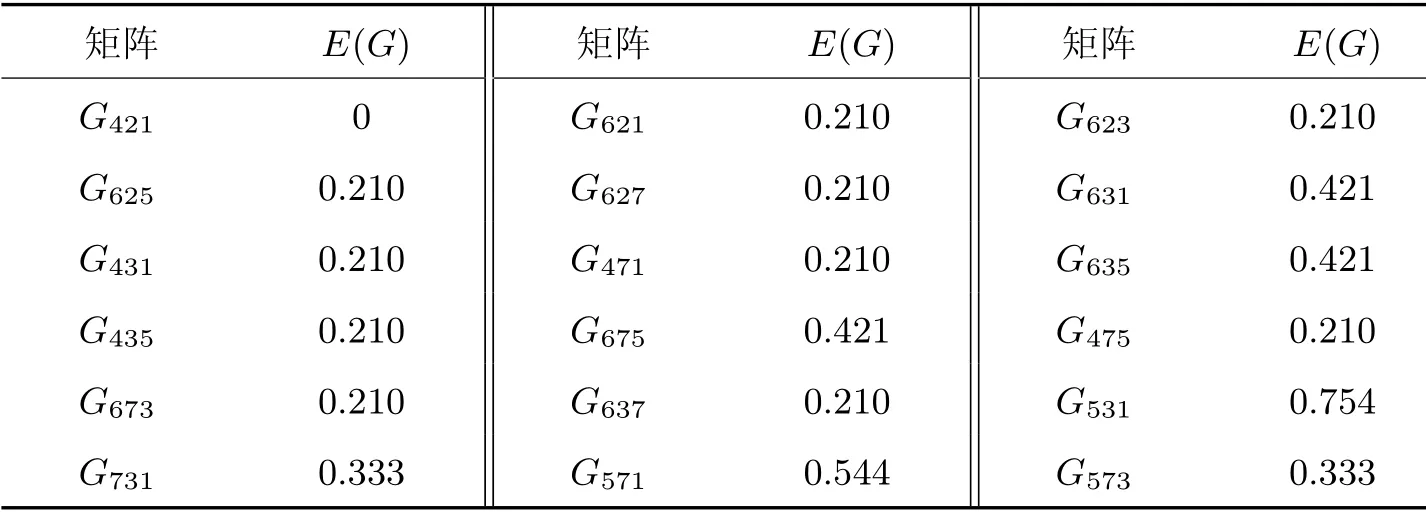
表1 3×3 核矩阵极化率Table 1 Polarizability of 3×3 nuclear matrix

2 l=3 终止极化码

2.1 终止极化原理

信道经过t次极化后，部分信道已经足够好，这部分信道不需要继续进行极化。通过设置终止门限Tg停止该部分信道极化

式中：ER为目标误帧率，N为极化码码长，E(G) 为对应核矩阵极化率。设置Tb=Tg-1 为差信道终止门限，若信道WiN满足Z(WiN) ≤Tg，则表示信道已经足够好，不需要继续极化，相应的节点称为好信道终止节点；若信道WiN满足Z(WiN)≥Tb，则表示信道已经足够差，也不需要继续极化，相应的节点称为差信道终止节点。若父节点为终止节点，则直接将子节点错误概率值设为父节点的错误概率值，即终止节点的子节点为终止节点。

根据目标误帧率ER构造终止极化码，并使用串行抵消（successive cancellation,SC）译码，由式（2）可知译码后其实际误帧率满足

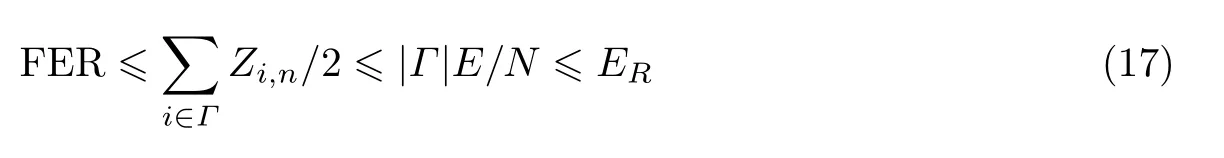
式中：Γ表示好信道集合，码长为N=3n。

2.2 终止极化码纠错性能分析

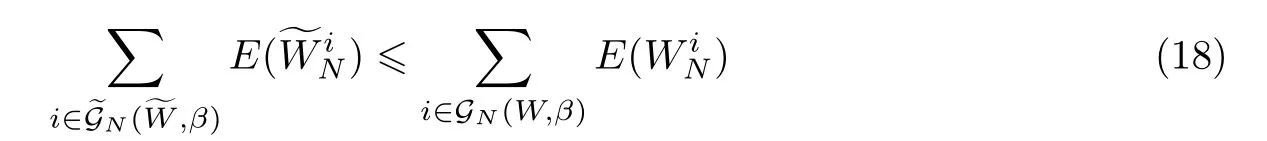
下面说明式（4）的证明过程。

核矩阵G531为为便于证明，令ςi=min{W(y|0),W(y|1)},ηi=max{W(y|0),W(y|1)}。根据式(1) 有因此BEC每个信道的错误概率均可计算得到。在不引起误解的前提下将每个信道的错误概率E(WiN)表示为E。基于核矩阵G531的极化码在进行极化时，其组合信道与原始信道的转换关系为(x1,x2,x3)=(u1,u2,u3)G531，表2为其具体的转化结果。

表2 G531 核矩阵转换结果Table 2 G531 kernel matrix conversion results

子信道的转移概率为

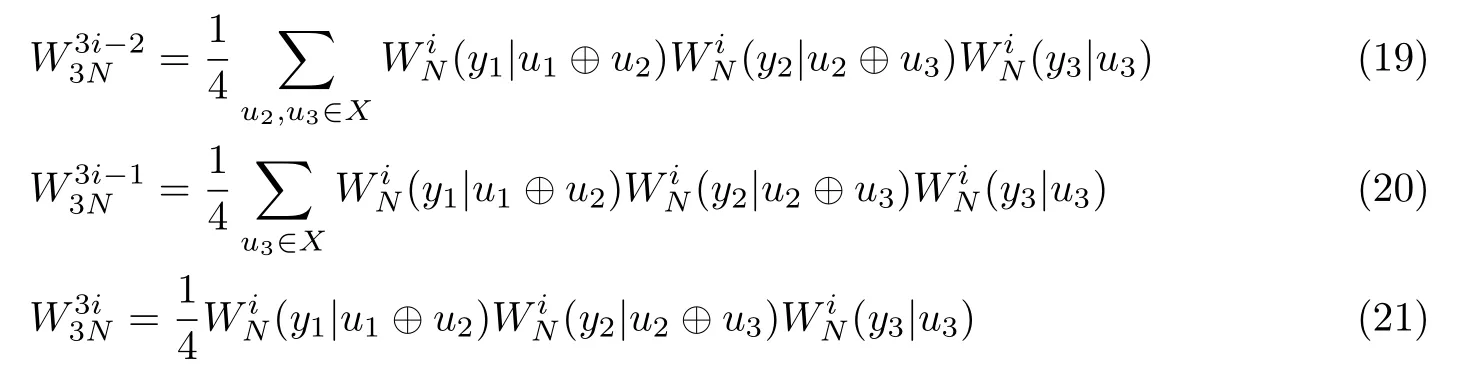
不失一般性，设WiN(y1|0) 为ςi，WiN(y1|1) 为ηi，则信道的转移概率可以表示为

或

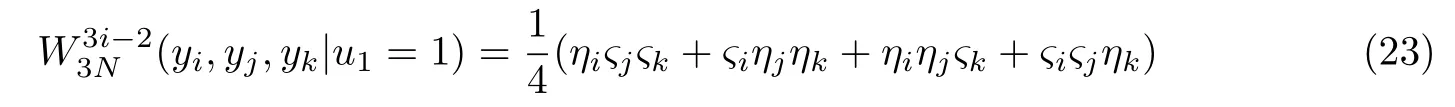
通过计算与比较得

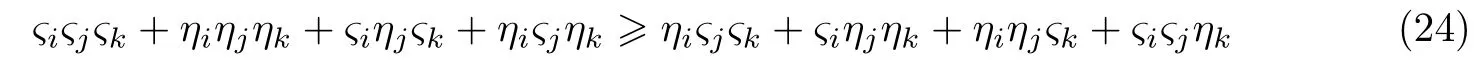
所以子信道为

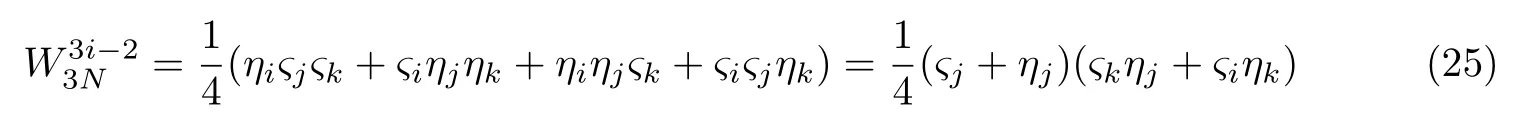
其错误概率为

经计算，子信道为

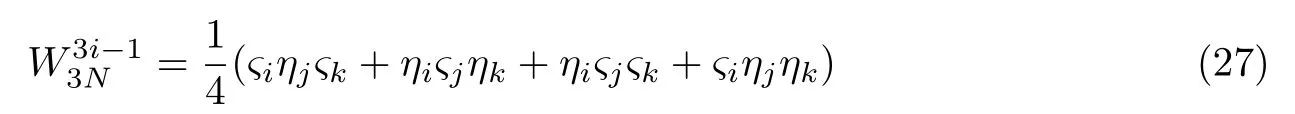
则有

子信道的错误概率为

定义ϑF为完全极化码的比特错误概率，可以写为

终止极化码的比特错误概率ϑS为

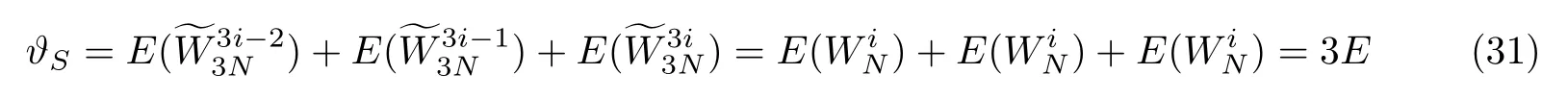
令

则

因为E(WiN)＜0.5，即E＜0.5，所以Δ＞0。因此，式(4) 成立，进一步得出基于3×3核矩阵G531的终止极化码的纠错性能要优于完全极化码。如果按照上述推导过程，假设终止极化码差信道集合表示为(,β)，其含义如同完全极化码里BN(W,β) 的定义，类似好信道推导过程，同样可以推导出终止极化码差信道的纠错性能要优于完全极化码，即有

2.3 CRR 的上下界分析

对于终止极化码的好信道，其终止门限为Tg，t层极化后最小巴氏参数为Z3t,t=p3t，p为擦除概率。如图1所示，当信道经过tg-1 次极化后，比特信道巴氏参数Zi,tg-1均大于Tg，而经过tg次极化后，至少有一个比特信道的巴氏参数小于Tg，即tg次极化后最右边子节点v3tg,tg的巴氏参数小于Tg，此时该节点不需要极化，后续(n-tg)2n-tg的极化步骤可以跳过。于是终止极化码好信道的CRR 上界为

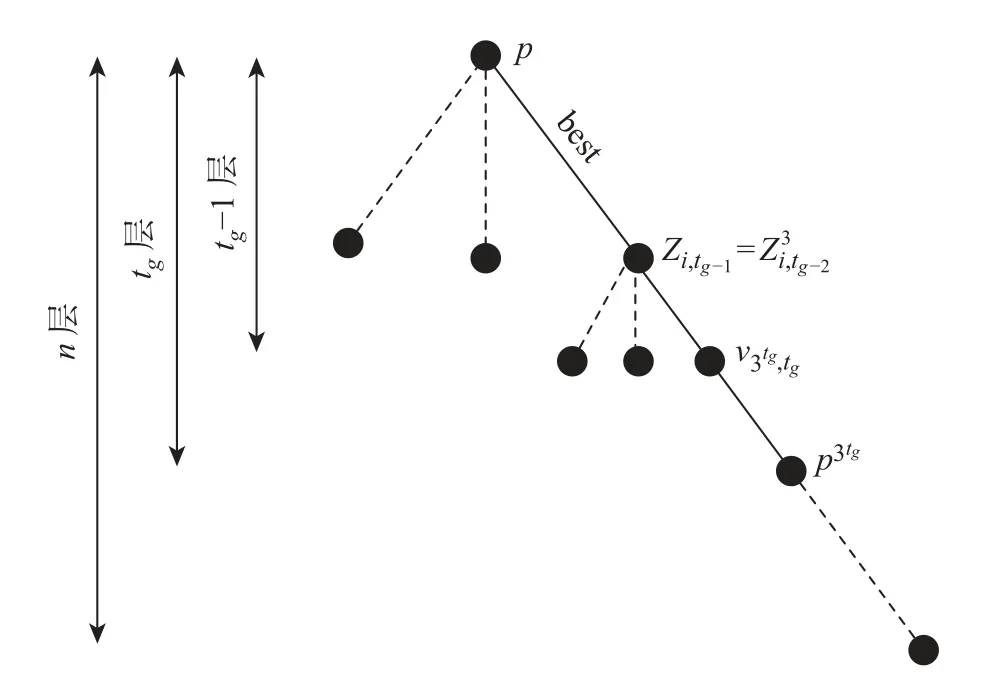
图1 复杂度降低上界Figure 1 Upper bound of complexity reduction

对于任一极化层t,设定阈值B,GB,t表示极化第t层所有比特信道的集合，且任一比特信道的巴氏参数都不超过B，即GB,t={i:Zi,t≤B}，存在定理1。

定理1对于任意阈值B，令tb=若极化层tγ≥tb，其中γ=则终止极化码好信道复杂度降低比的下界为

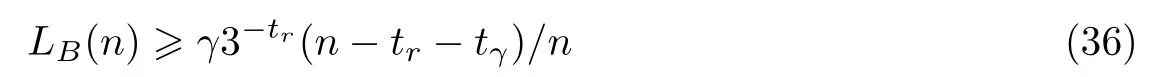
证明因为tγ≥tb，所以集合GB,tγ非空。在极化层tγ中，对于GB,tγ中任一个节点，若至少存在一个子节点的巴氏参数小于Tg，即GB,tγ中任一个节点最右边的子节点的巴氏参数最大可为B3tγ，且B3tγ≤T，则在极化层tγ+tr，至少有γ3γ=|GB,tγ|个节点的巴氏参数小于Tg。每个节点终止极化可跳过的极化步骤数共为

于是总共可跳过γ3tγS步极化步骤，与原极化步骤数比值为γ3tγS/(n3n)，所以复杂度降低比的下界为γ3-tr(n-tr-tγ)/n。

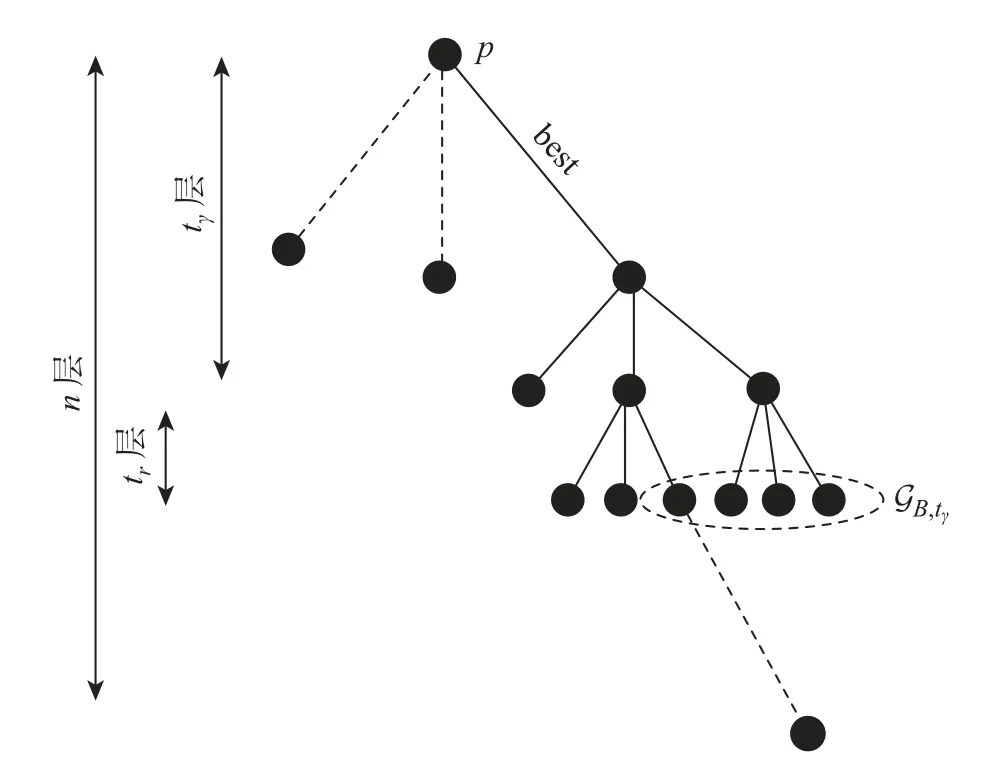
图2 复杂度降低比的下界Figure 2 Lower bound of complexity reduction

3 仿真与结果

为验证所提的基于3×3 高维核矩阵的终止极化码的可行性，本文以下列模拟参数进行实验仿真。

表3 模拟参数Table 3 Simulation parameters

基于以上的分析与证明，在码长为N=37的情况下，设定目标误帧率为10-5，由表1知G531的极化率为0.754，根据式(3) 计算出终止极化码好信道的终止门限Tg为6.064×10-9。在BEC 信道上构造终止极化码，运用Matlab 仿真出终止极化码复杂度降低比与擦除概率p的关系。计算CRR 的上下界，令如图3为终止极化码CRR 与其上下界的对比。

图3 当目标FER 为10-5 时终止极化码好信道复杂度降低比Figure 3 Terminal polarization code good channel complexity reduction ratio when target FER is 10-5

图3中UB 表示CRR 上界，LB 表示CRR 下界。仿真表明终止极化码好信道的CRR可以用其上下界来表征，当目标FER 为10-5时甚至可以实现高达71.43% 的复杂度降低比。随着p的增大，好信道的CRR 逐渐减小。这是由于p增大，信道极化到足够好需要极化的次数更多，能够跳过的极化步骤就更少，所以CRR 减小。差信道终止门限Tb=1-Tg，且差信道对改善FER 不起作用，而给出的目标FER 是相对于全部信道，下面给出全部信道在FER=10-5时终止极化码的复杂度降低比。图4中曲线AC 表示终止极化码全部比特信道的CRR 随p发生的改变，GR 表示好比特信道的CRR 随p发生的变化。

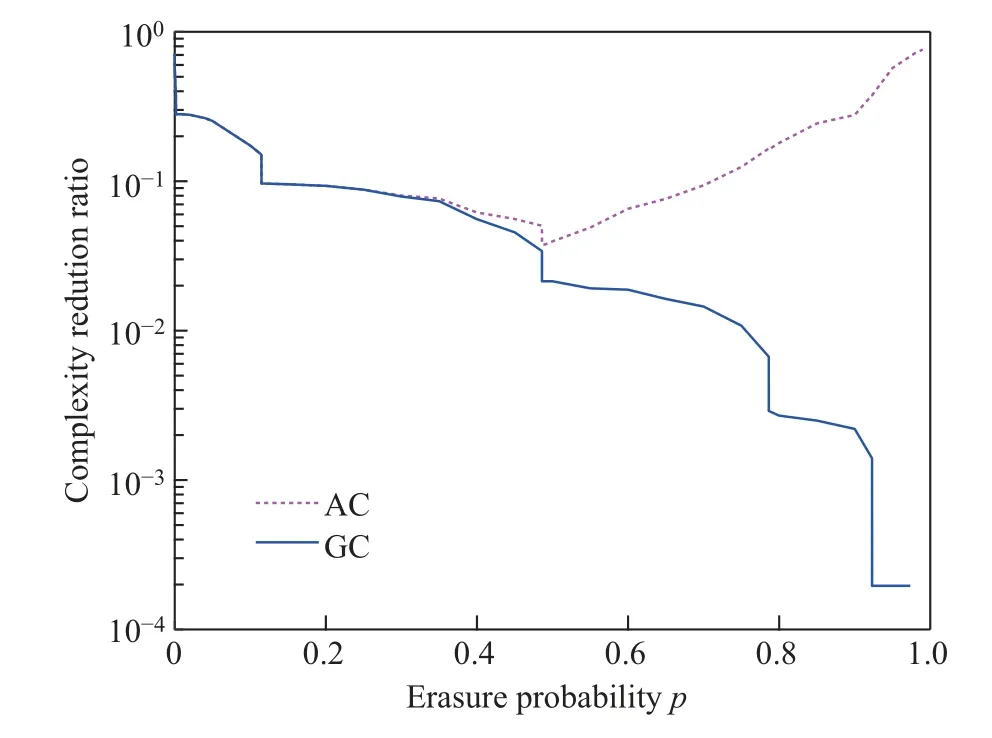
图4 当目标FER=10-5 时终止极化码复杂度降低比Figure 4 Complexity reduction ratio of termination polarization code when target FER=10-5

图4中曲线AC 能够反映出终止极化码全部比特信道的CRR 随擦除概率p发生的改变，GR 反映了好比特信道CRR 随p发生的变化。仿真表明在目标误帧率为10-5时，G531核矩阵构造的终止极化码在p=0.5 附近时其复杂度降低比最小。这是因为虽然差信道对改善译码FER 不起作用，但随着p的增大，达到差信道终止阈值需要的极化操作就越少，可以省去的极化步骤越多，所以全部比特信道的CRR 随着p的增大呈现图中AC 线条的走势。AC的仿真表明，在BEC 信道上终止极化码可以大大降低编译码计算量，从而降低串行抵消译码因顺序计算而造成的时延。

本文提出的终止极化码是根据译码后需满足的目标FER，设定相应的终止门限T，减少不必要的极化操作步骤，从而降低编译码的计算复杂度。在BEC 信道上设定需要达到的不同目标FER 时，终止极化码好信道可以实现的复杂度降低比如图5所示。

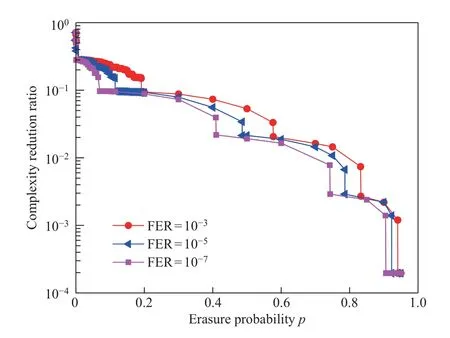
图5 不同目标误帧率下的复杂度降低比Figure 5 Frame error rate complexity reduction ratio for different targets

仿真表明：随着擦除概率p的增大，终止极化码好信道的CRR 逐渐变小，即终止极化码好信道计算复杂度降低的能力逐渐变小。且随着要求所需达到的目标误帧率越小，CRR 也逐渐减小，如图5所示，在BEC 上擦除概率相同的情况下，目标误帧率为10-3时的CRR 最大，目标误帧率为10-5时次之，目标误帧率为10-7时复杂度降低比最小。因此，在实际应用中，可根据通信链路条件和所需达到的通信质量来设定终止阈值，从而设计出满足不同需求的通信链路系统。

为证明3×3 高维核矩阵终止极化码的误码率性能，本文采用3×3 高维核矩阵的终止极化码与两种不同构造方法的极化码（巴氏参数构造的3×3 高维核矩阵极化码和2×2 核矩阵的终止极化码）进行SC 译码分析对比。如图6所示，2×2 核矩阵的终止极化码与3×3 高维核矩阵的终止极化码采用的码长分别为（1 024,2 048）、（1 093,2 087），两种方法的码长比较接近，以保证其BER 性能对比的公正性。当误码率为10-2时，3×3 高维核矩阵极化码较2×2 核矩阵的终止极化码有0.3 dB 的性能增益，3×3 高维核矩阵的终止极化码误码率性能明显优于2×2 核矩阵的终止极化码。同时，传统构造方法（巴氏参数）的3×3 高维核矩阵极化码与3×3 高维核矩阵的终止极化码的译码性能几乎一致。因此，3×3 高维核矩阵的终止极化码在保证3×3 高维误码率性能的同时其计算复杂度也较低。

图6 高维核矩阵的终止极化码SC 译码性能Figure 6 SC decoding performance of the terminating polarization code of the high-dimensional kernel matrix

4 结 语

本文提出了3×3 极化核构造终止极化码的方案，并严格证明了所提方案的可行性，给出了终止极化码复杂度降低比的上下界值，定量地分析了终止极化码对编译码计算复杂度的降低比。文中给出的CRR 上下界比较宽松，在之后的工作中可进一步使两值逼近。最后，对所构造的终止极化码进行仿真验证，结果表明，根据所需达到的目标误帧率不同而设定相应阈值，终止极化码在不影响性能的情况下能不同程度地降低复杂度。