科学研究中的化归思想在化学问题解决中的应用讨论

张文广,计从斌*,丁百林,过文学

(1.上饶师范学院 化学与环境科学学院,江西 上饶 334001;2.上饶中学,江西 上饶 334000)

何为化归?顾名思义,化归即转化和归结。把有待解决的问题,通过思维变换,转化、归结为某个比较容易解决的问题并最终解决它,这样的思想方法,称为化归思想。它的哲学基础是事物的普遍联系和变化发展等唯物辩证思想。

化归思想是人们思考问题和解决问题的一种独特的思维方法,在科学研究和教育教学中均具有广泛的应用。

1 科学家运用化归思想进行科学研究的典型案例

化归思想可以为科学研究启迪智慧、引导方向、优化思路、修正偏差,这方面具有很多实例,可以给我们深刻启示。

(1)理想气体状态方程pV＝nRT虽然是从实验事实中总结出来的规律,但只有在足够低的压力和较高的温度下才适合于真实气体。对于压力较高、温度很低的实际气体,上述状态方程会产生较大的偏差。科学探究偏差产生的原因,人们发现主要是由于忽略气体分子本身的体积和分子间的相互吸引作用引起的。1873年,荷兰科学家范德华(van der Walls)针对这种情况,就理想气体状态方程适用于实际气体进行了修正,提出了著名的范德华方程,其表达式如下:

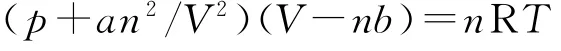
上式考虑了真实气体分子本身的体积及分子间的相互作用力,对理想气体状态方程进行了两项修正。第一项修正是考虑体积因素:由于气体分子本身是有体积的,扣除了这一体积才是分子自由运动的真正空间,它才相当于理想气体的体积。假设一摩尔气体的体积为b,则V理想＝V－nb。第二项修正是考虑压力因素:气体分子间的作用力对压力也有影响:气体分子运动到容器内壁时,分子间的相互吸引作用一定会削弱分子本身对器壁的碰撞,这必定会使得体系的实测压力比按理想气体处理而产生的压力更小,所以在实测压力的基础上应该加上由分子间引力而导致的压力减小才相当于理想气体的压力。又如何推定气体分子间本身引力对体系压力的影响呢?可以这样考虑:一方面,气体分子对容器内壁的碰撞是弹性碰撞,弹性碰撞产生的压力正比于气体的浓度n/V;另一方面,分子间的相互吸引导致体系压力减小,其减小值也正比于气体的浓度n/V,综合考虑之,体系的压力校正项应该是an2/V2,即p理想＝p实际＋an2/V2(式中a为比例常量,不同的气体有不同的数值,须由实验确定,国际制下其单位为Pa·m6·mol－2)[1]。

上述例子是科学研究中将对象从实际状态化归为理想状态的典型案例。

(2)根据原子光谱及更进一步的研究,科学家得出了氢原子及类氢离子(He＋或Li2＋)等单电子体系核外电子能量的求算公式:

式中的Z为原子的核电荷数,n为电子所处的电子层。上式说明,原子的核电荷数越大,或电子所处的运动空间离核越近,其受到原子核的吸引力越大,能量越低。那么又如何求算多电子原子中核外电子所具有的能量呢?

在多电子原子体系中,不仅存在原子核对各电子的吸引作用,还有电子之间的排斥作用。科学家为了问题研究的方便,往往把其他电子对被讨论电子的排斥作用,看作相当于屏蔽或抵消了一部分核电荷对它的吸引作用,所以,原子核对所讨论电子产生吸引作用的有效核电荷(Z*)为:

σ被称作屏蔽常数,相当于其他电子对所讨论电子的总的屏蔽效应,代表着对核电荷吸引作用的抵消部分,在精度要求不高的情况下,其值可用Slater规则计算[2]。通过这样的处理之后,对多电子原子中的某个电子来说,其能量就可用单电子原子类似的公式来求算了:

上述例子是科学研究中将对象从复杂问题(多电子原子)化归为简单问题(类似于单电子原子)的典型案例。

从上述实例中,我们可以得到这样的启示:化归是一种独特而极富价值的思想方法,在科学研究中具有重要的作用.

2 化归是问题解决的思维法宝

通过检索,我们发现,到目前为止,在化学方法论教育类研究文献中,系统研究化归思想的内容几乎很少看到。实际上,化归思想在化学教学或化学问题解决中具有极其广泛的应用。从科学家研究问题、处理问题的思路,我们可以得到启发:在教学中面对纷繁复杂的化学问题,尤其是化学计算问题,引导学生通过化繁为简,化隐为显,化零为整,化实为虚等灵活的思维变换,也许能够达到化难为易、使问题得以顺利解决的目的。

2.1 活用守恒原理,将繁杂化归简单

“天下大事,必作于细;天下难事,必作于易。”把繁杂问题化归为简单问题,是问题解决的不二法门。

例1:已知Cu、Ag元素的相对原子质量分别为64和108。14 g铜银合金与足量某浓度的HNO3反应,产生的气体在标况下与1.12 L O2混合后通入水中恰好完全吸收而不剩任何气体,求合金中Cu、Ag的物质的量[3]。

分析:HNO3与Cu、Ag反应时其还原产物有NO2和NO,其量比关系随HNO3浓度的不同而不同;NO2在H2O中可歧化反应生成HNO3和NO,NO(包括HNO3被还原得到的产物及NO2在水中歧化得到的产物)又可被O2氧成NO2。显然,本问题涉及的反应及数量关系过于复杂,无法通过合金与HNO3、NO2与H2O、NO与O2的连锁反应来解题。实际上,如果我们弱化惯性思维,另辟蹊径,抓住氧化－还原这一对立统一过程得失电子数必定相等这一守恒原理(Cu、Ag被氧化所失去的电子数应等于HNO3被还原所得到的电子数,同时也等于NO被氧化所失去的电子数,还等于O2被还原时所得到的电子数,见图1),问题就迎刃而解了。

图1 氧气和铜银在硝酸转化中的氧化－还原作用

解:设合金中Cu、Ag的物质的量分别为x和ymol,则有:

解上述联合方程,得x和y分别为0.05和0.01 mol。

2.2 巧赋物质数值,将隐晦化归显明

把无数据的隐晦问题赋予适当的数值,使其成为显明的问题,可能就比较好解决了。

例2:将木炭和CaCO3的混合物在空气中加热,使CaCO3完全分解,木炭完全氧化成CO2。若产物中CO2的质量与原CaCO3的质量相等,则原混合物中木炭的质量是多少(已知C、O和Ca的相对原子质量分别为12、16和40)?

分析:对于无物质数量的隐晦问题,巧妙的解决办法是根据其相对分子质量适当赋值,使问题明朗化。解:本问题涉及的化学反应为:

设原混合物中CaCO3的质量为100 g(CaCO3的相对分子质量值),根据上述反应可知,木炭氧化生成的CO2

与100 g CaCO3分解生成的CaO质量相同,等于56 g。故木炭的质量为56×12/44＝15.27(g)。

2.3 善找对象通式,将零散化归整体

把问题中的多个零散分子化归为一个整体变式分子,让思路“曲径通幽”,往往就会使问题“柳暗花明”。

例3:在硫化钠、硫酸钠和亚硫酸钠三种物质组成的混合物中,若氧元素的质量分数w为0.22,则钠元素的质量分数是多少?在甲醛、乙酸和丙酸三种物质组成的混合物中,若氧元素的质量分数w为0.48,则碳元素的质量分数w是多少?

分析:两种混合物中,都含有三种元素,但只已知一种元素的质量分数。只有求出其他两种元素的量比关系及总的质量分数,才能得出其中各种元素的相对含量。而其他两种元素的量比关系必须通过化归思想才能确定:将硫化钠(Na2S)、硫酸钠(Na2SO4)和亚硫酸钠(Na2SO3)三种分子的化学通式变换为Na2S·On(n值分别为0,4,3),将甲醛(CH2O)、乙酸(C2H4O2)和丙酸(C3H6O2)三种分子的化学通式变换为(CH2)m·On(m分别为1,2,3;n值分别为1,2,2),问题也迎刃而解了。

解:(1)硫化钠、硫酸钠和亚硫酸钠混合物的通式可表示为Na2S·On,故:

钠、硫元素(Na2S组合)的总质量分数w(Na2S)＝1－0.22＝0.78,

钠元素的质量分数w(Na)＝0.78×23×2/(23×2＋32)＝0.46。

(2)甲醛、乙酸和丙酸混合物的通式可表示为(CH2)m·On,故:

碳、氢元素(CH2组合)的总质量分数w(CH2)＝1－0.48＝0.52,

碳元素的质量分数w(C)＝0.52×12/14＝0.447 5。

2.4 多作类比迁移,将陌生化归熟悉

类比迁移,就是根据两个或两类特定对象之间存在某些方面的相似或可联系之处,进而推出它们在其他方面也可能相似的逻辑推理或信息迁移的方法。把类比推理运用到教学中去,将熟悉问题迁移到陌生问题上,也能使问题解决取得积极的效果。

例4:(1)硼和氮可生成二元固体聚合物,试指出这种聚合物的可能结构;(2)无机苯B3N3H6在常温下是一种无色液体,具有芳香气味,许多物理性质相似于苯,化学性质比苯更活泼,易发生加成反应。画出无机苯的结构,并写出其与HCl加成的反应式[4]。

分析:只要有等电子体的概念,并找到中学已熟悉的等电子分子,进行结构和性质方面的类比迁移,问题不难解决。

解:(1)BN与C2是等电子体,根据等电子原理,氮化硼与碳单质具有相似的结构。实验表明,氮化硼有类似于金刚石和石墨两种常见晶型结构,前者是结构基元为四面体的三维空间大分子结构(图2(a)),N、B的原子轨道都采取sp3方式杂化;后者是以平面六边形为结构基元的二维片层大分子(图2(b)),N、B原子轨道都呈sp2杂化。两种晶型结构中,N、B原子间都有配位键存在(分别为σ配键和π配键)。

图2 金刚石型BN的结构单元(a)和石墨型BN的结构单元(b)

(2)无机苯B3N3H6与有机苯C6H6是等电子分子,根据等电子原理,它们具有相似的分子结构(见图3),其中的C、B、N原子轨道都呈sp2杂化,分子内都有离域π66键。无机苯与HCl的加成类似于双键的加成,富电子的Cl－应加在缺电子的B上,缺电子的H＋应加在富电子的N上(见图4)。

图3 有机苯(a)和无机苯(b)的分子结构

图4 无机苯与HCl的加成反应

2.5 虚构中间过程,将一步化归多步

根据多重平衡共存－互动思想[5],很多化学反应都可以看作是分步进行的,反应体系中存在着多个化学平衡,它们之间相互依存,相互影响。由化学热力学中的盖斯定律或状态函数的性质可知,化学反应不管是一步进行还是分几步进行,只要始、终态一定,体系状态函数的改变值如自由能变或焓变、熵变值不变。因此,有时为了问题解决的需要,可以把问题中一步进行的过程化归为多步进行的过程。

例5:(1)已知Ag2C2O4的Kspθ＝3.5×10－11,电对Ag＋/Ag的电极电势φθ＝0.799 V,试求电对Ag2C2O4/Ag的φθ。

(2)已知碱性介质中氯元素的电势图如下,试求电对Cl O3－/Cl－的φθ的值。

分析:根据反应体系多重平衡共存－互动思想,所求电极反应:

可看作分下列两步进行,各物质平衡浓度关系服从化学平衡关系式:

步骤(2)中没有电子得失,不会有电极电势产生;所求电极反应即总式(1)中的电子得失实际上是通过步骤(3)来实现的。所以,总式(1)产生的电极电势实际上是步骤(3)的电极电势。

解(1):根据上述分析,结合能斯特方程及相关定量关系,有:

依题意,当总式(1)中C2O42－的浓度为1 mol/L时,其电极电势即为Ag2C2O4/Ag电对的标准电极电势,故:

解(2):类似上面的分析,所求电极反应:

可看作由下列三步完成:

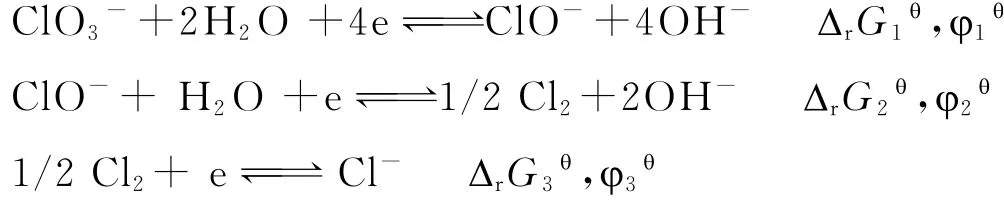
根据状态函数的性质有:

2.6 外推目标极限,将实际化归理想

把目标推至极端,或将实际状态问题化归为理想状态问题,也是问题解决的有效方法。

例6:(1)图5是273 K时CH3F蒸气的ρ/p～p图,求CH3F的摩尔质量M;(2)标况下将NO2、NO、O2混合起来,充满于一密闭容器内,最后把容器注满水,气体全部消失,无一剩余,求所得溶液的物质的量浓度范围[4]。

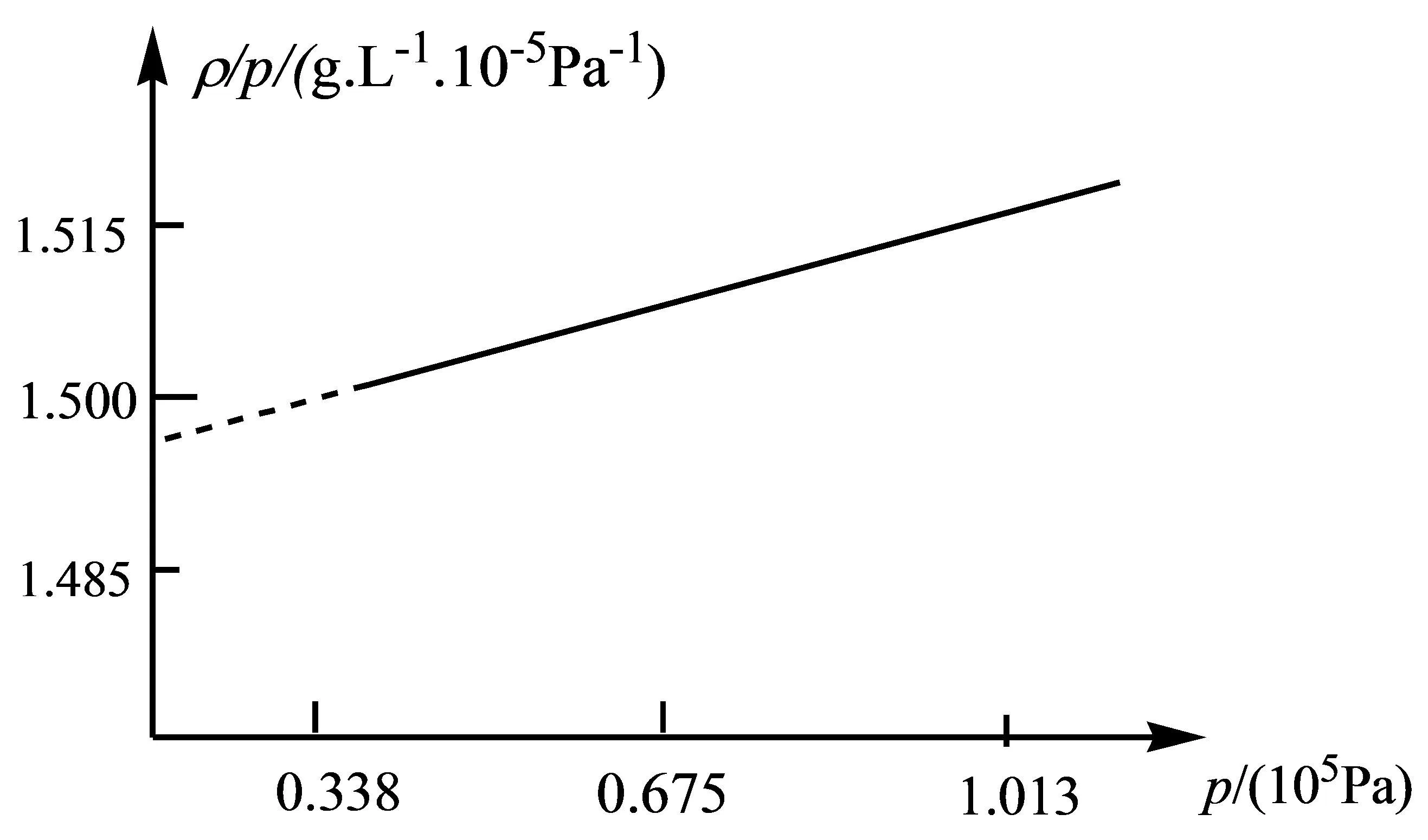
图5 CH 3 F的ρ/p～p关系

分析:(1)根据理想气体状态方程pV＝nRT＝mRT/M,可推得M＝(ρ/p)RT,故理想气体在恒温下ρ/p应该是一常数(水平线),但图5所示并非如此,说明CH3F并非理想气体,但只要把图中直线外推至p＝0时,就可认为是理想气体了。

(2)假设容器的体积为V升,题中涉及的化学反应有:当反应全按③进行时,生成的HNO3浓度值应为(4V/5)/22.4V＝1/28;当反应全按④进行时,生成的HNO3浓度值应为(4V/7)/22.4V＝1/39.2;

题设情境理当落在这两个极端之间。

解:(略)

3 结语

教学中只要善于动脑、敢于总结,还可以归纳出很多类似的问题化归方法。教学实践中运用上述方法时,关键是要对化学的基本概念、基本原理、基本公式清楚明白,解决问题的思路才会清晰明了。

世上没有一成不变的事物,当我们在问题解决的过程中遭遇困扰的时候,试试变换思路,找找通幽曲径,也许就能从“山重水复”的迷境中走出来,欣赏到“柳暗花明”的美景,甚至让问题解决的方案变得多种多样、多姿多彩!