不平衡数据分类的类依赖属性加权朴素贝叶斯算法改进

樊顺星, 李楚进, 沈澳

(1.华中科技大学数学与统计学院, 湖北 武汉 430074;2.华盛顿大学文理学院, 华盛顿 西雅图 98195)

1.引言

不平衡数据分类问题是近年来机器学习领域的重要研究内容.不平衡数据是指数据集内不同类的样本数量失衡, 即一个类的样本数量很少, 另一个类的样本数量却很多, 此时我们把样本数量少的类叫做少数类, 把样本数量多的类叫做多数类.不平衡数据在疾病诊断、风险管理、生物学等领域经常出现.比如在进行癌症早期筛查时, 检测者中健康人的数量远大于癌症患者.传统分类方法是以总体分类效果为指导的, 所以受多数类的影响较大, 进而在分类决策时偏向于把样本分到多数类.这样的分类偏向导致传统分类方法对于少数类的分类效果不佳,而在现实中人们往往更在意少数类的分类效果.因此, 即使传统分类方法能在不平衡数据分类中取得较高的总体分类正确率, 但依然无法满足人们的现实需要.如何改进传统分类方法使其能胜任不平衡数据分类成了一个热点问题.不平衡数据的分类策略主要分为两个层面: 数据层面和算法层面.

数据层面.这类方法通过减少多数类样本(欠采样)或增加少数类样本(过采样)的方法使不平衡数据集变为平衡数据集.欠采样时, 若是直接随机移除多数类数据, 则有可能恰好把某些重要的多数类数据移除, 进而损失多数类分类的重要信息, 极大损害总体分类性能.所以常用EasyEnsemble等算法获得欠采样的平均效果[1].过采样时, 如果直接简单重复已有的少数类样本, 可能会造成过拟合.为避免这个问题, 常用SMOTE等算法合成新的少数类样本[2-3].

算法层面.这种方法不改变数据集的原始分布, 而是对传统算法进行修改使其能用于不平衡数据分类或是提出新的不平衡分类算法.其中最常用的是代价敏感学习.它给少数类设置更高的错分代价, 给多数类设置较低的错分代价, 然后以整体错分代价最小化为目标确定模型.这样做能减少在分类决策时传统分类器对于多数类的偏向.人们已经把代价敏感学习应用在了许多传统的分类方法上, 例如支持向量机[4]、K邻近[5]、决策树[6].

另一方面, 关于朴素贝叶斯分类器用于不平衡数据分类的研究较少.但是关于改进朴素贝叶斯总体分类能力的研究较多.例如通过最大化CLL或最小化MSE目标函数来确定权重值的一般属性加权朴素贝叶斯模型WANBIACLL、WANBIAMSE.[7]以及通过最大化CLL或最小化MSE目标函数来确定权重值的类依赖属性加权朴素贝叶斯模型CAWNBCLL、CAWNBMSE.[8]这些属性加权方法能增强朴素贝叶斯对训练数据的拟合能力, 进而减少现实数据违反条件独立性假设所带来的不良影响, 提高朴素贝叶斯的总体分类性能.

但是这些改进朴素贝叶斯模型依然在不平衡数据分类中存在对多数类的偏向性, 无法胜任不平衡数据分类任务.且与传统分类算法在二分类问题中可以通过调节分类阈值来调节少数类的召回率与精确率不同的是, 属性加权朴素贝叶斯算法估算出的后验概率不符合概率定义, 有可能正类和负类的后验概率都大于0.5, 所以无法视作是根据分类阈值进行分类决策, 进而无法通过调节分类阈值的方法调节少数类的召回率与精确率.

针对原始的朴素贝叶斯拟合能力不强、属性加权后的朴素贝叶斯无法通过调节分类阈值来调节少数类的召回率和精确率这两个缺点, 本文提出了CAWNBλ-CLL、CAWNBλ-MSE, 实验证明, 这两个算法既有较强的总体分类能力, 也可以通过调节λ对少数类的召回率、精确率进行调节, 从而适用于不平衡分类任务.

2.常见类依赖属性加权

Ⅰ 类依赖属性加权方法

一般的属性加权方法是给每个属性分配一个权重值, 也就是说权重值只与属性相关, 比如表2.1的加权模式.

类依赖属性加权顾名思义是一种更细致的属性加权, 它的权重值既与属性相关又与类相关.类依赖属性加权方法在K邻近分类器[9]、朴素贝叶斯分类器[8]的相关研究中都有应用.

Ⅱ CAWNB

类依赖属性加权朴素贝叶斯(CAWNB)顾名思义就是将类依赖属性加权应用在朴素贝叶斯上的一种算法[8].它跟朴素贝叶斯的最大不同就是在估算后验概率时它将所有的条件概率的指数由1改成了它所对应的权重值.

CAWNB估算后验概率(这里的后验概率是不符合概率定义的)的公式如下:

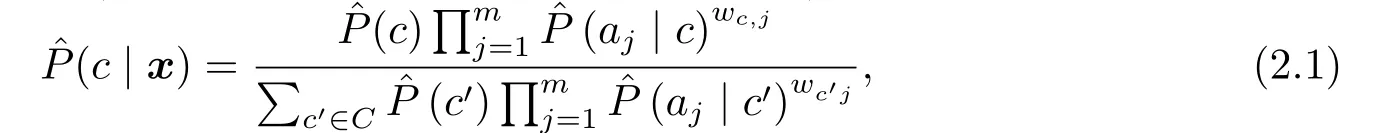
其中先验概率和条件概率的估算公式为:

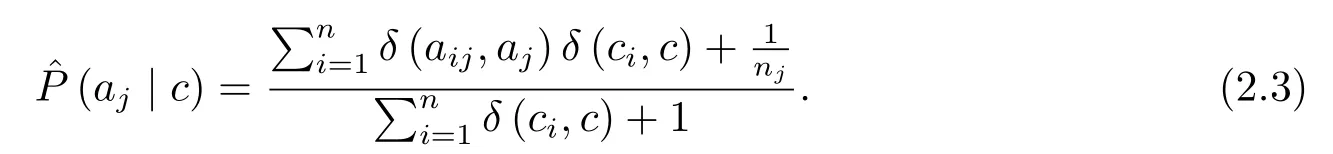
(2.1)式中的权重值确定方法是利用优化算法L-BFGS最大化或最小化以权重矩阵为自变量的目标函数, 进而确定最优的权重值.

最后根据最大后验概率原则进行分类决策:

3.用于不平衡数据分类的CAWNB

为了能使CAWNB运用在不平衡数据分类上, 所以本文考虑在目标函数的数学形式上削弱多数类对目标函数的影响.

常用的目标函数有条件对数似然(CLL)和均方误差(MSE):

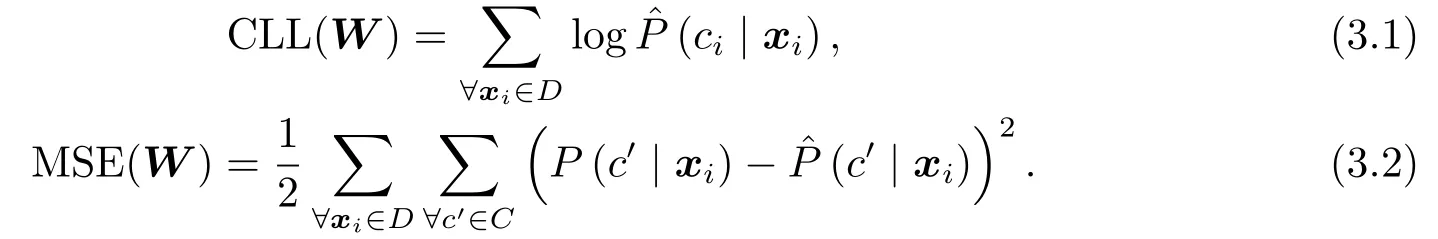
假设c是少数类, 则对目标函数中的多数类部分乘上平衡系数λ,λ的取值一般为0到1之间的实数, 这样做是为了减弱多数类对于目标函数的影响, 让优化算法更专注于优化少数类的分类情况.由此提出两个新的目标函数:

以λ-CLL 和λ-MSE为目标函数的类依赖属性加权朴素贝叶斯算法分别记作CAWNBλ-CLL和CAWNBλ-MSE, 算法的步骤总结如下:

算法:CAWNBλ-CLL/CAWNBλ-MSE

输入: 训练数据D, 待预测实例x

1) 根据(2.2)式和(2.3)式分别估算先验概率和条件概率;

2) 利用L-BFGS优化算法,λ-CLL /最小化λ-MSE , 从而确定最优权重矩阵W;

3) 根据式(2.1)估算后验概率;

4) 根据式(2.4)将实例分到具有最大后验概率的类标签.

4.实验评估

本文采用的四个数据集均来自UCI机器学习数据库, 其中多分类数据集会将相似类进行合并, 把其转换成二分类数据集.数据集的基本信息如表4.1所示.

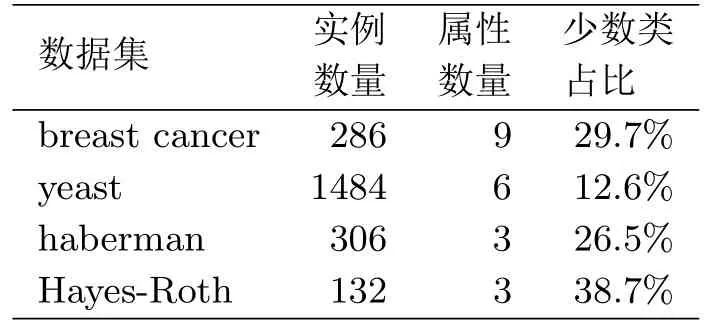
表4.1 数据集的基本信息

Ⅰ 平衡系数λ的作用

平衡系数λ的预期作用是改变分类器的分类偏向进而调节少数类的召回率与精确率.然而对于朴素贝叶斯分类器可以运用更直接的方法调节召回率、精确率, 那就是调节分类阈值.由于原始的朴素贝叶斯分类器可以看作是以分类阈值0.5 在进行分类决策, 即当正类的后验概率大于0.5则将待预测实例分到正类, 否则分到负类, 那么我们通过调节分类阈值一样可以改变分类器的分类偏向进而调节少数类的召回率与精确率.

所以本节的实验有两个作用, 一是验证λ是否真的可以调节召回率和精确率, 二是将上述两种调节召回率和精确率的方法进行对比.

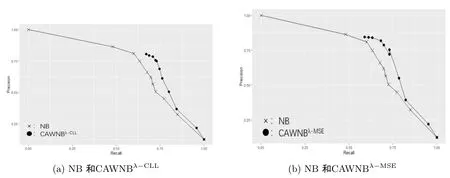
图4.1 调节λ与调节分类阈值的效果对比

以yeast数据集为例,λ和分类阈值取遍0、0.1、0.2、...、0.9、1.以横轴为召回率, 纵轴为精确率,×代表朴素贝叶斯, 实心圆代表本文算法, 画出少数类召回率、精确率与λ和分类阈值的关系.

从图4.1中可以看出调节CAWNBλ-CLL、CAWNBλ-MSE的平衡系数与调节朴素贝叶斯的分类阈值的作用是类似的, 都可以对分类器的召回率和精确率进行调节.并且本文算法在Precision-Recall图中比调节分类阈值的朴素贝叶斯更加靠近右上角, 这说明在绝大多数情况下, 本文算法的调节效果好于直接调节分类阈值的朴素贝叶斯.

关于λ的选择: 在处理实际的不平衡数据分类任务时, 既可以根据领域专家经验人为选择符合实际需求的λ, 也可以利用搜索算法, 在训练集上建模, 以F 指标或G指标这类的召回率与精确率的综合指标为指导, 让计算机自动选择λ的值.

Ⅱ 算法性能

为了评估合适取值的CAWNBλ-CLL、CAWNBλ-MSE算法在实际数据集上的性能, 本文在breast cancer和haberman数据集的实验中选择λ= 0.4, 在yeast和Hayes-Roth的实验中选择λ= 0.5, 做分层十折交叉验证, 并与原始的朴素贝叶斯做对比, 实验结果如表4.2和图4.2所示.

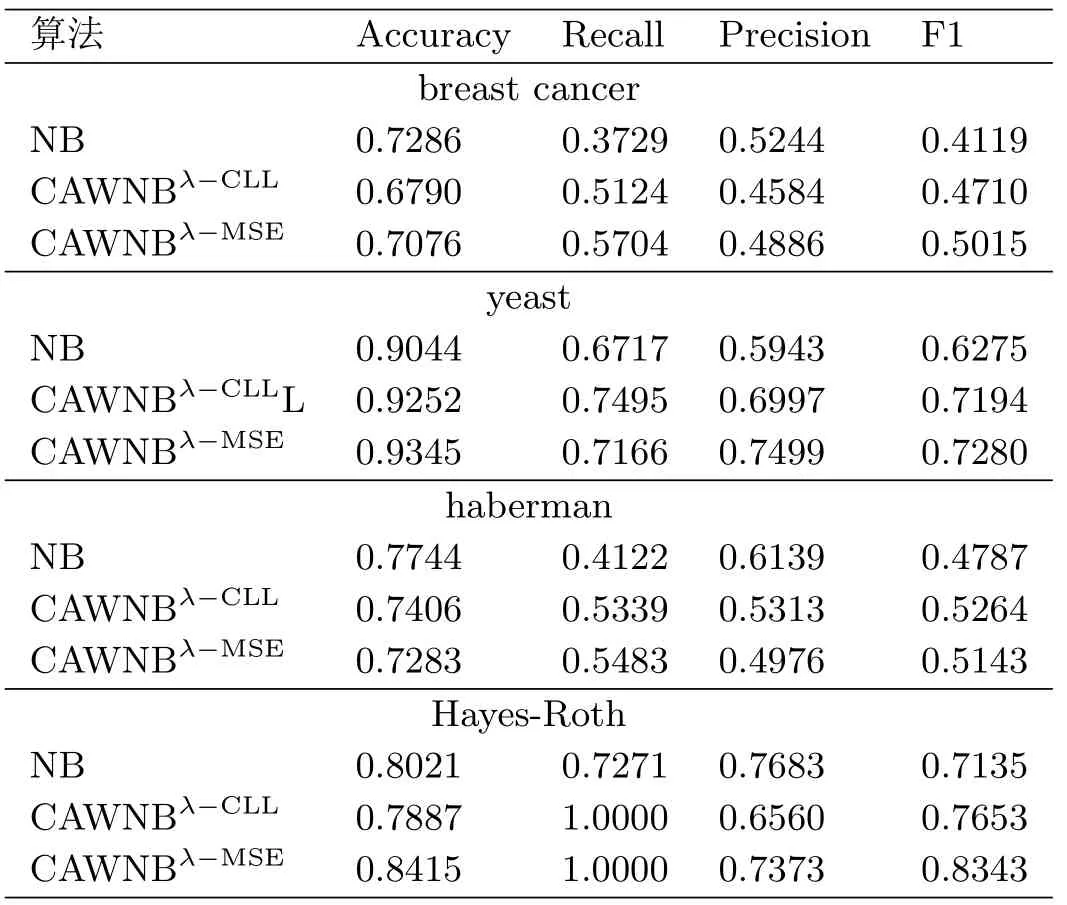
表4.2 4种数据集上的分类结果

图4.2 4个数据集分类结果的平均值

由图4.2可以看出, 合适取值的CAWNBλ-CLL、CAWNBλ-MSE算法在F1值和召回率上明显优于朴素贝叶斯, 在正确率上与朴素贝叶斯相近.这说明本文算法在不平衡数据分类问题中表现良好, 并且在不过分影响总体正确率的情况下改变了分类器对于多数类的分类偏向, 使得分类器对于少数类有较高的识别率.

5.结论

本文针对不平衡数据分类任务提出了CAWNBλ-CLL、CAWNBλ-MSE算法.实验证明本文方法简单有效.本文算法主要有两个作用: 一是能通过调节λ来调节分类器的分类偏向, 进而调节少数类的召回率与精确率, 并且这种调节方法比直接调节阈值更有效; 二是选择了合适的λ值后, 算法可以胜任不平衡数据分类任务, 即在不过分影响总体分类效果的情况下提高少数类的召回率, 进而获得较高的F1值.