一类Moran集的拟对称packing极小性
付晓慧 李彦哲
(1.广西大学数学与信息科学学院, 广西 南宁 530004;2.广西大学广西数学研究中心, 广西 南宁 530004)
1.引言
拟对称映射是一类重要的映射, 它比双Lipschitz映射更广泛, 与双Lipschitz映射最本质的区别是它可以改变分形维数, 拟对称极小集是关于拟对称映射如何影响和改变分形集合的分形维数这个课题的一个重点研究对象.关于拟对称Hausdorff极小性, 国内外学者得到了大量的经典结果.[1-9]相比较拟对称Hausdorff极小性, 关于拟对称packing极小性的结论就要少一些, 主要的结论都是在实直线上, 特别是Moran集上完成的.Kovalev[4]证明了实直线上拟对称packing极小集的packing维数要么为0, 要么为1; LI、WU和XI[10]证明了实直线上两类特殊的packing维数为1的Moran集是拟对称packing极小集; WANG, WEN[8]证明了所有packing维数为1的齐次Cantor集是拟对称packing极小集; YANG, WU和LI[9]将文[8]中的结果推广到一类packing维数为1的齐次完全集上.
本文利用质量分布原理, 证明了实直线上一类特殊的Moran集为拟对称packing极小集, 在一定条件下推广了文[10]的结果.
本文在第二节介绍一些预备知识, 包括拟对称映射、Moran集与递减Moran集的定义; 第三节给出本文的主要结果; 第四节对主要结果进行了证明.
2.预备知识
定义2.1[11](拟对称映射) 设X,Y为两个度量空间, 称同胚f:X →Y为(η- )拟对称映射.若存在一个同胚η:[0,∞)→[0,∞)使得对X中任意三个不同的点a,b,x都有

如果X=Y= Rn, 则称f为n维拟对称映射.对于集合E ⊂Rn, 如果对于任意n维拟对称映射f,都有dimHf(E)≥dimHE(dimPf(E)≥dimPE),则称E具有拟对称Hausdorff(packing)极小性, 称E为拟对称Hausdorff(packing)极小集.
本文研究Moran集的拟对称极小性, Moran集是一类重要的分形集, 被国内外分形几何学者广泛研究, 下面给出Moran集的定义.

令Fk={Iσ:σ ∈Ωk}, 则F=k≥0Fk={Iσ:σ ∈Ω}, 称Fk中的元素Iσ为E的k阶基本区间.
注2.1不失一般性, 本文总假设对∀k ≥1,σ ∈Ωk-1, 闭区间Iσ*1,Iσ*2,··· ,Iσ*nk是从左往右排列的.
对Moran集的基本区间长度做一定的要求, 可以定义递减Moran集.
定义2.3[13](递减Moran集) 设E ∈M(I,{nk},{ck,j}), 如果存在正整数a使得对任意k ≥1都有k+a阶基本区间的长度小于k阶基本区间的长度, 则称E为递减Moran集.
注2.2齐次Moran集[12]是满足a=1的递减Moran集.
关于Moran集更多经典结论见文[14-16].
3.主要结果

从而若E为满足c* >0和dimP E= 1的递减Moran集, 则由定理3.1得到对任意1维拟对称映射f都有dimP f(E)=1.由上面的讨论知定理3.1在递减Moran集的条件下推广了文[10]中定理2的结论.
4.主要结果的证明
定理3.1证明的关键是用质量分布原理对支撑在拟对称映射像集上的概率测度做估计, 质量分布原理如下.

为了使用质量分布原理来估计拟对称映射像集的packing维数, 需要定义一个支撑在拟对称映射像集上的概率测度μd, 下面定义μd并利用引理对其做估计.
设E ∈M(I,{nk},{ck,j}),Iσ为E的k阶基本区间.由f是同胚映射知f(Iσ)是R的一个区间.类似地, 也称f(Iσ)为f(E)的k阶基本区间.令Jσ=f(Iσ).
固定d ∈(0,1), 定义μd(f([0,1]))=1, 对任意k ≥1,f(E)的任意基本区间Jσ(σ ∈Ωk), 定义
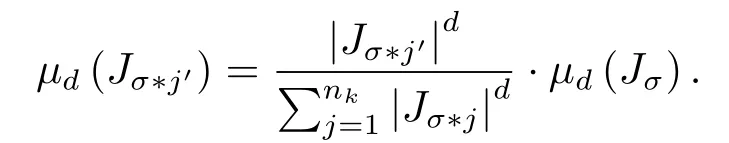
由测度扩张定理知,μd可唯一扩张成支撑在f(E)上的概率测度.
设k >1,σ ∈Ωk-1, 记

当σ=φ时, 记

下面4个引理来源于文[10], 在后面的证明中将会被使用到.

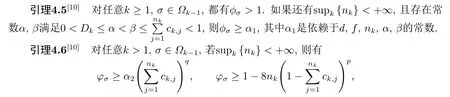
其中λ,p,q是引理4.2中的常数,α2是依赖于f,nk的常数.

对∀k ≥1, 令

根据引理4.6可得

从而要证明(4.5), 只需证当t →∞时, I→0, II→0, 且III→0.
由引理4.7结论(B)知, 当t →∞时

由引理4.7结论(A)知, 当t →∞时

由引理4.7结论(C)知, 当t →∞时
在醇类燃料中氧分含量较高,因此,燃烧更加充分,燃烧的效率也更高,另外在燃烧过程中不会出现大量排放一氧化碳的状况,但是甲醇本身具有较大的危害性,同时还有腐蚀性,故而甲醇汽车在现阶段很难得到广泛的应用。

其中第二个不等号利用了不等式log(1-t)≥-2t对任意t ∈[0,1/2)成立.
由(4.6), (4.7)和(4.8)可得(4.5)成立, 从而完成了引理4.8的证明.
利用引理4.8可得到下面这个重要命题.
命题4.1设E ∈M(I,{nk},{ck,j})为满足supk{nk} <+∞的递减Moran集, 且存在常数α ∈(0,1)和满足=s*的子序列{kt}t≥1, 使得

成立.若s*=1, 则对于任意1维拟对称映射f, 都有dimP f(E)=1.
证任取x ∈f(E).∀k ≥1, 令Jk表示满足x ∈Jk的f(E)的k阶基本区间, 则J1⊃J2⊃J3⊃···.由于E为递减Moran集, 从而存在正整数a使得对∀k ≥1, 都有k+a阶的基本区间长度小于k阶的基本区间长度.令P=min{t:kt >2a-1},Tt=t+1-P.
对∀k ≥1, 用Mk,i(i= 1,2,··· ,Nk)表示E的k阶基本区间的长度, 其中Nk=n1n2···nk,注意到gx(α)=|f-1(B(x,α))|是连续映射, 所以存在序列{rTt}t≥P, 使得

从而

所以f-1(B(x,rTt))与E的kt-2a-1阶基本区间至多相交2个, 这意味着f-1(B(x,rTt))与E的kt阶基本区间至多相交2(supknk)2a-1个, 即B(x,rTt)与f(E)的kt阶基本区间至多相交2(supknk)2a-1个.
记与B(x,rTt)相交的f(E)的kt阶基本区间为则

由引理4.8得

注意到对∀1≤i ≤h都有

从而有
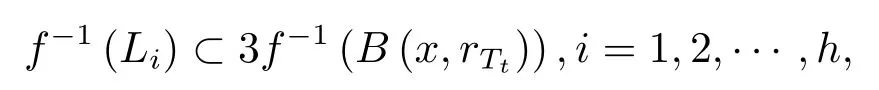
其中3f-1(B(x,rTt))是与f-1(B(x,rTt))同心、长度为3|f-1(B(x,rTt))|的区间.由引理4.2得

其中K >0为常数.联立(4.9)可得

注意到当t →∞时,rTt →0.所以对∀x ∈f(E), 存在常数C >0, 使得

由引理4.1和(4.11)可得
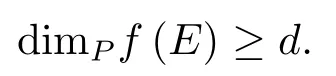
再由d的任意性得到dimPf(E)=1.
有了命题4.1, 就可以快速完成定理3.1的证明.
定理3.1的证明设E ∈M(I,{nk},{ck,j})为满足定理3.1的条件的递减Moran集, 则E显然满足命题4.1的条件.又因为从而若dimPE= 1, 则由引理4.3可得s*= 1,这样由命题4.1就可以得到, 对于任意1维拟对称映射f, 都有dimPf(E)=1.
- 应用数学的其它文章
- 不确定离散时间输入饱和系统的鲁棒预见控制
- Maximal Operator of (C,α)-Means of Walsh-Fourier Series on Hardy Spaces with Variable Exponents
- Empirical Likehood for Linear Models with Random Designs Under Strong Mixing Samples
- 带分数阶边值条件的差分方程组的正解问题
- An Interior Bundle Method for Solving Equilibrium Problems
- 纵向数据下非参数带测量误差的部分线性变系数模型的估计

