闭子模中K-框架的几个新的不等式

相中启, 肖祥春

(1.新余学院数学与计算机学院, 江西 新余 338004;2.厦门理工学院应用数学学院, 福建 厦门 361024)

1.引言

1952年, Duffin和Schaeffer[1]正式定义了框架的概念.1986年, Daubechies等[2]发现了框架理论和小波理论之间的密切联系, 自此框架开始成为研究的热点.因许多好的性质, 目前框架已在量子力学、抽样理论、声学、信号处理等诸多领域得到了广泛的应用.

另一方面, 框架概念被类比到了HilbertC*-模的情形[3], 这为我们提供了框架理论研究的新途径.值得注意的是, 由于C*-代数的复杂性以及HilbertC*-模与Hilbert空间的本质差异,致使HilbertC*-模中的框架问题要远比Hilbert空间来得复杂.此外, 已有研究表明, HilbertC*-模理论与小波特别是框架理论在许多方面都有着紧密的联系, 这促使越来越多的学者将关注点投向HilbertC*-模中框架的研究[4-7].

作为框架的拓广,K-框架的概念最早出现在关于算子的原子分解的工作中[8].因与框架在许多性质上的显著差异性以及潜在的重要应用,K-框架已得到了国内外众多学者广泛而深入的研究[9-11].最近, 文[12]将K-框架的概念推广到了HilbertC*-模中并研究了K-框架在新的架构下的一些性质.

在研究信号重构的有效算法时, Balan等[13]发现了著名的Parseval框架恒等式.在对这些恒等式做进一步研究时, 他们得到了Parseval框架的一个有趣的不等式.随后, G˘avrut¸a[14]将该不等式推广到一般框架和交替对偶框架的情形.借助于文[13-14]的思想, 最近一些学者又建立了Hilbert空间和HilbertC*-模中广义框架的一些不等式[15-18].受上述工作的启发, 本文利用K-对偶给出了HilbertC*-模的闭子模中K-框架的一些新的不等式, 所得结果可自然推导或类比产生文[13-14,18]中的相应结果.

2.定义和引理

本节回顾证明主要结论所要用到的一些定义, 以及可伴算子的一些基本事实.

如果C=D= 1, 则称F是Parseval框架.如果只有(2.1)式右端的不等式成立, 则称F是界为D的Bessel序列.

设F={fj}j∈J是H的框架, 则它可以诱导一个自伴的正可逆算子, 称为F的框架算子,定义如下

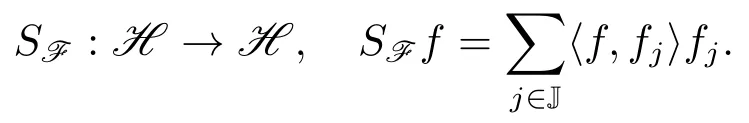
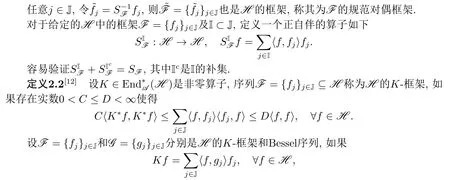
则称G是F的K-对偶.此时称(F,G)是一K-对偶框架对.

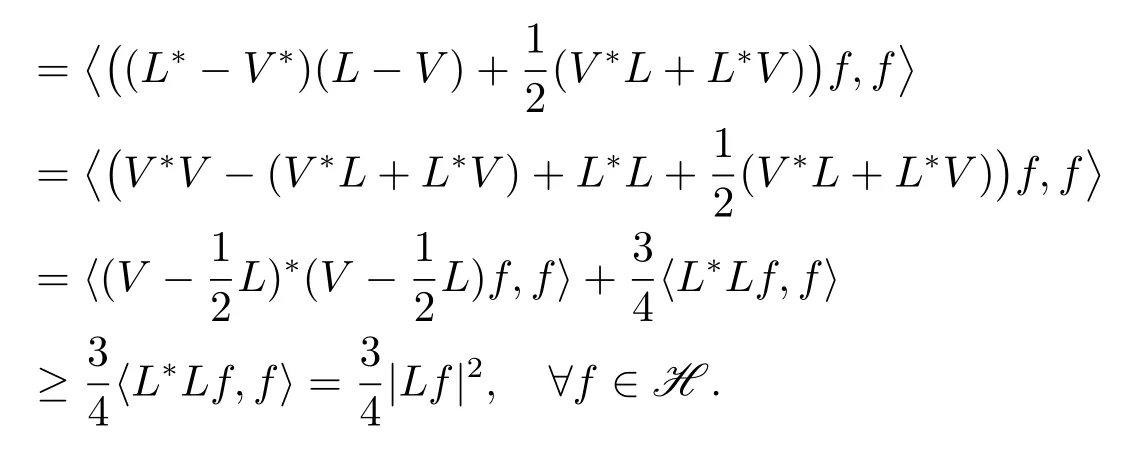
3.定理及其证明

因此

由于Range(K)是闭的, 联合引理2.1和(3.3)式可得

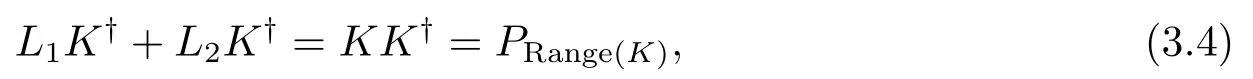
其中PRange(K)表示Range(K)上的正交投影.故此

任意f ∈Range(K)和λ ∈R, 由引理2.2可得

由此可知

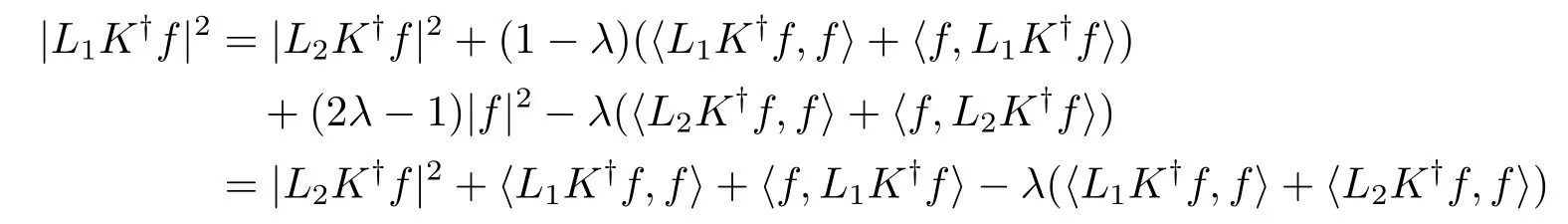
于是

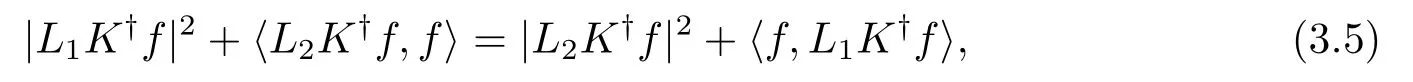
这表明

下证(3.1)式中的不等式.再次利用引理2.2有

于是

这就完成了证明.

任意I⊂J, 直接计算可得

类似地, 有

因此在(3.7)式中取aj=即得结论.

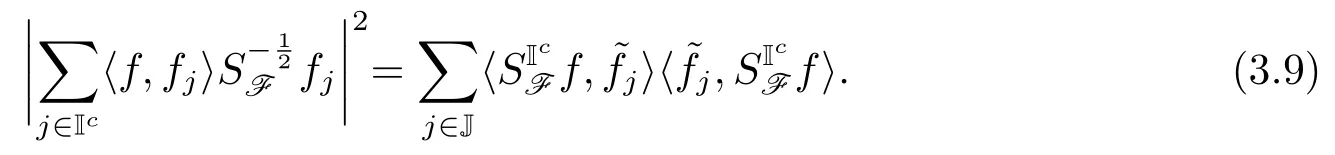
由推论3.1立即可得

推论3.2设F={fj}j∈J是H的Parseval框架, 则对任意的I⊂J,f ∈H及λ ∈R, 有

再次利用引理2.2, 则“此外”部分的结论由下述不等式可得:

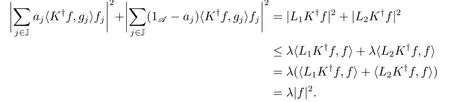
推论3.3设F={fj}j∈J是H的框架, 则对任意的I⊂J,f ∈H及λ ∈[1,+∞), 有

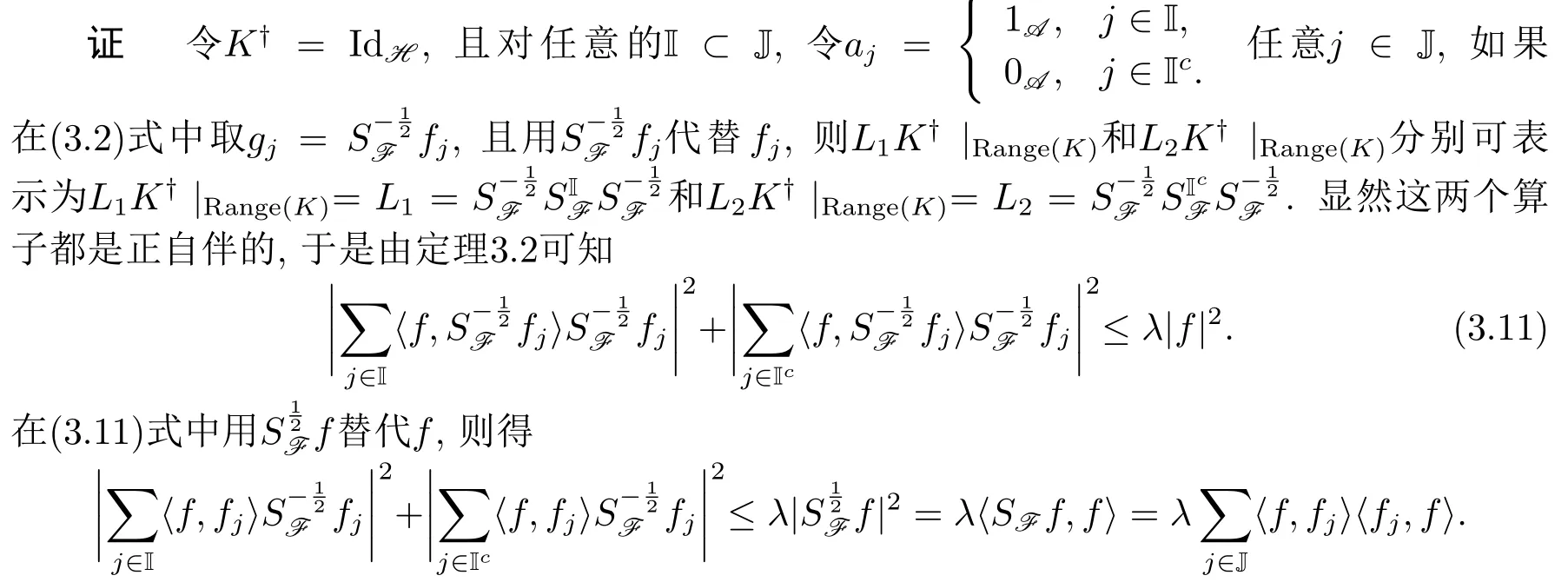
由此式及(3.8)、(3.9)式可得(3.10)式右侧的不等式.(3.10)式左侧的不等式可以通过类似的讨论得到.

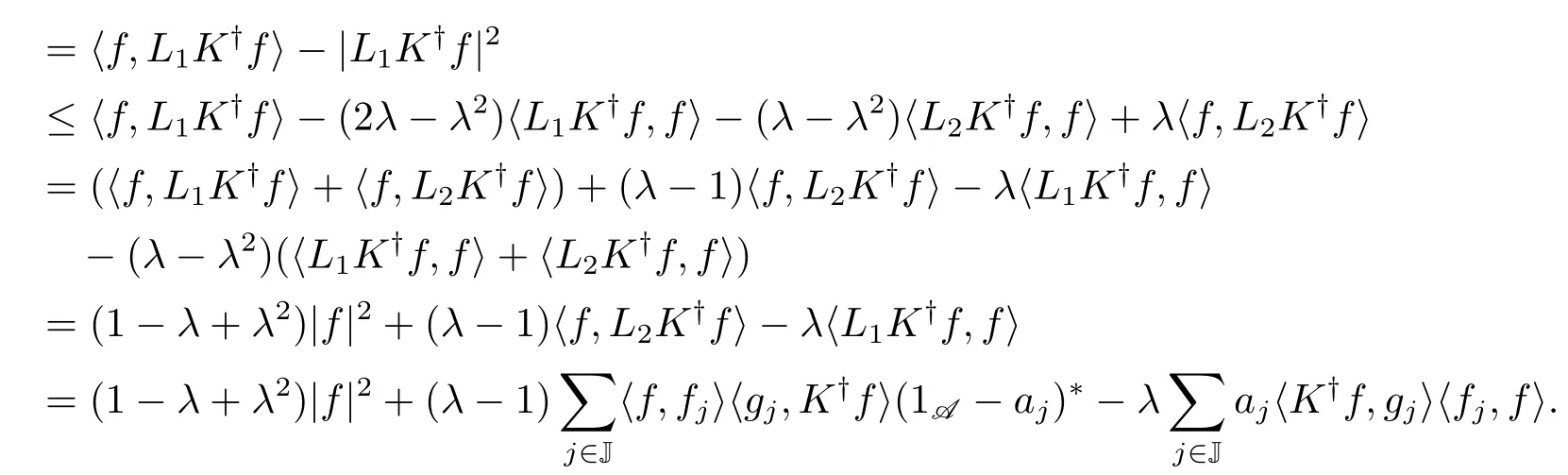
现在, 由(3.5)式可得“此外”部分的结论:

推论3.4设F={fj}j∈J是H的框架, 则对任意的I⊂J,f ∈H及λ ∈[1,+∞), 有

证 证明类似于推论3.3, 故略去.

由引理2.3可知

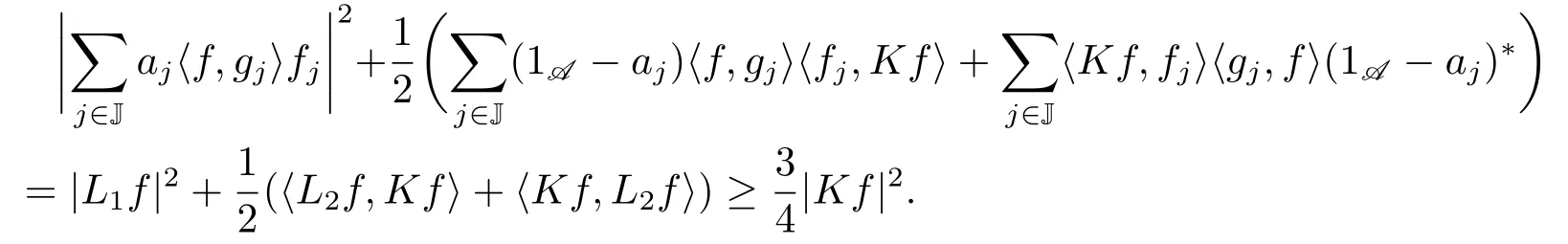
另一侧的不等式由下式给出: