计及电气特性的空调负荷建模及集群控制策略

刘志伟，苗世洪，杨炜晨，张世旭，梁志峰，汪 鹏

（1. 华中科技大学电气与电子工程学院强电磁工程与新技术国家重点实验室电力安全与高效湖北省重点实验室，湖北 武汉 430074；2. 国家电网有限公司，北京 100031；3. 国网湖北省电力有限公司电力科学研究院，湖北 武汉 430077）

0 引言

微电网具有节能降耗、运行灵活、供电可靠性高的特点，一直是新能源领域研究的热点［1］。然而，微电网中风电、光伏等分布式电源（DG）出力的随机性与间歇性给电网的稳定性以及电能质量带来了严重影响［2-3］。目前，在微电网中通过装设大量的储能设备来平抑分布式电源的功率波动，然而储能设备的建设与运行费用昂贵，在经济性方面不具有优势［4］。

近年来，高级量测体系以及智能能量管理系统发展迅速［5］，使得感知并控制终端负荷成为可能。同时也推动了需求响应技术的发展。直接负荷控制作为激励型需求响应的一种［6］，可以增加需求侧弹性，有效解决新能源接入下微电网功率的波动问题。其中，以空调负荷（ACL）为代表的温控负荷凭借其响应速度快、调节潜力大［7］等特点已成为需求响应的重要资源。据统计，在我国夏季用电高峰期，空调负荷占负荷尖峰的比例达到30%～40%［8］，具有巨大的调控潜力。通过直接负荷控制调控温控负荷集群，能够有效平抑微电网中新能源的功率波动，减小对储能设备的投资。因此研究温控负荷的集群调控策略，对于维持微电网稳定运行，提高微电网运行的经济性具有重要意义。

温控负荷具有复杂的热-电特性，其储热特性与电气特性相互影响加大了调控难度，因此对其精准控制依赖于准确的模型和完善的控制策略。对于温控负荷的建模，现有文献大部分只考虑了温控负荷的热力学模型以及热电转换关系［9-10］，并未充分分析其电气特性。对此，文献［11］使用感应电动机模型来模拟空调负荷，研究了在电压扰动下，空调负荷的稳态运行特性；文献［12］使用三相异步电动机来描述空调负荷，通过对大量电动机进行聚合，建立了空调负荷聚合模型；文献［13］通过实际实验研究了定频空调的运行特性，详细分析了其静态特性、动态特性、启动过程以及堵转过程，建立了完善的电气模型。然而文献［11-13］均只分析了空调负荷的电气模型，未考虑空调负荷的储热特性及利用其储热能力参与电网的调控，因此对于空调负荷的建模有待进一步完善。

温控负荷集群控制策略可分为群内控制策略与集群整体控制策略两部分讨论。针对群内控制策略，文献［14］首先提出一种基于温度排序的状态队列算法，然而该算法会造成部分设备频繁启停，影响使用寿命；在此基础上文献［15］引入了分组约束，提出考虑用户舒适度的温度优先序列控制策略，在一定程度上减小了热泵的启停次数，但在特定情况下热泵的频繁启停问题仍然突出；文献［16］针对热泵频繁启停问题设置了最小控制时间约束，避免了对热泵的连续控制，但仍未能较好解决热泵频繁启停问题。另有文献通过调节温度设定值来实现对温控负荷的控制［3，10］，控制过程中并不涉及设备的频繁启停问题，但改变了室内温度，影响了用户舒适度。因此，如何在满足用户舒适度的前提下对温控设备的启停特性进行改善，成为目前亟需解决的问题。

针对集群整体控制策略，文献［17］以电冰箱为例，提出变用户参与度的控制策略，实现对孤立微电网的功率波动平抑，维持系统频率的稳定，减小了对储能装置的容量需求；文献［18］建立了空调负荷集群暂态模型，并提出基于跟踪微分器的优化控制策略，在保证用户舒适度的情况下，实现了调频辅助服务，优化了调控成本；文献［19］将电热水器应用到电力系统的低频减载中，考虑用户行为的影响，建立了温控负荷集群模型，并进一步建立了其需求响应策略架构，为系统提供了调频服务。此外，部分文献对空调负荷与其他可控单元的协调控制策略［20-21］开展了研究。然而上述文献只考虑了有功功率调节或将负荷视为恒功率模型，并未深入分析负荷电压变化对控制策略的影响，无法保障在实际电网环境下控制策略的有效性。

综合以上分析，在温控负荷建模方面，现有研究均只单独分析了温控负荷的热力学模型与电气模型，未将二者综合考虑；在温控负荷集群群内控制方面，现有研究采用温度优先序列控制，未能较好解决负荷频繁启停问题，影响设备使用寿命；在集群整体控制方面，现有研究将负荷理想化为恒功率模型，未深入分析负荷功率与电网电压的双向影响。因此，亟需对温控负荷的建模与控制策略进行更深入的研究。

本文在上述研究的基础上，以空调负荷作为研究对象，提出计及电气特性的空调负荷集群控制策略。首先，综合考虑空调负荷的储热特性与电气特性，构建了完善的空调负荷模型；其次，在温度优先序列算法的基础上，进一步结合调节空调温度设定值的控制思想，提出一种基于改进温度优先序列的空调负荷集群群内控制策略，保证用户舒适度的同时，优化了群内空调的启停特性；最后，考虑调控过程中负荷节点电压变化对空调负荷集群功率的影响，提出了基于下垂控制的空调负荷集群策略，在计及电压及集群等效荷电状态的约束下，实现对控制指令的准确响应。仿真结果表明，在所提的集群控制策略下，空调负荷集群能够有效平抑微电网中风电引起的功率波动，保障微电网的安全稳定运行。

1 空调负荷集群控制模型构建

1.1 空调负荷模型

空调负荷作为典型温控负荷，在用户中使用普遍，具有良好的储热特性，调控潜力巨大。本文选择制冷空调作为研究对象，分别构建空调负荷的热力学模型与电气模型。

1.1.1 空调负荷热力学模型

空调负荷热力学模型主要描述了室内温度的动态变化过程。在工程上，一般使用一阶等效热参数（ETP）模型，该模型主要考虑了室内与室外的热交换过程，如附录A图A1所示。

室温变化的一阶微分方程为：

式中：Qac为空调制冷量，单位为kW；Tin为室内温度，单位为℃；Tout为室外温度，单位为℃；Ra为建筑物的等效热阻，单位为℃／kW；Ca为建筑物的等效热容，单位为kJ／℃。

定频空调运行时功率不能连续调节，仅通过开启与停止2 种状态的不断转换来维持室内温度的稳定。室内温度变化过程如图1 所示。图中，Tset为空调设定温度，室内温度在其上限值Tmax、下限值Tmin之间波动；θ为温度死区。当室内温度高于Tmax时，空调开启，室内温度逐渐下降，此时空调以额定功率持续运行；当室内温度下降到Tmin时，空调关闭，室内温度逐渐上升，当上升至Tmax时，空调再次开启，如此循环，维持室内温度的稳定。

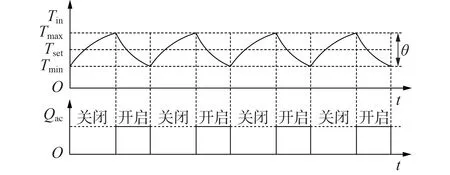
图1 空调负荷动态特性Fig.1 Dynamic characteristics of air conditioning load

1.1.2 空调负荷电气模型

空调负荷的电功率与制冷量的关系为：

式中：η为空调的性能系数；P为空调电功率，单位为kW。对于定频空调，其性能系数近似为定值［9］。

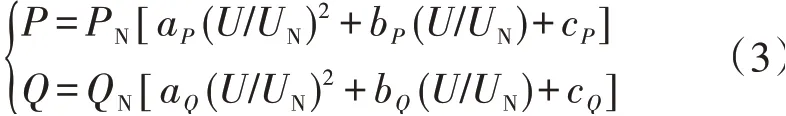
根据文献［13］，在运行时空调负荷功率会随着负荷节点电压的变化而改变，其负荷特性可由恒阻抗-恒电流-恒功率（ZIP）静态电压模型描述，如附录A图A2所示，电压静态特性表达式为：式中：Q为空调负荷的测量无功功率，单位为kvar；PN、QN分别为空调负荷的额定有功功率和无功功率，单位分别为kW、kvar；U、UN分别为空调负荷测量电压和额定电压，单位均为V；aP、bP、cP、aQ、bQ、cQ为功率系数。

1.2 改进群内温度优先序列控制

假定空调负荷集群中有N0台空调，在任一时刻，按运行状态可将空调负荷集群分为开启群与关闭群：

当集群自由运行时，各空调按照自身运行特性改变开关状态，集群总体上表现为一种随机负荷；当集群参与调控时，集群控制中心通过改变集群中处于开启或关闭状态空调的数量，以改变集群整体功率，从而满足电力系统的运行需求。

为有序地调控集群中各空调负荷的运行状态，前期研究提出了一种考虑用户舒适度约束的温度序列算法。其基本步骤如下：①确定当前时刻空调负荷的开启群与关闭群；②对开启群与关闭群中的空调进行排名，根据所采集到的室内温度，对开启群中的空调按室温升序排列，对关闭群中的空调按室温降序排列；③在温度上下限［Tmin，Tmax］之间设置可控温度范围［Tmin，TH］与［TL，Tmax］（TH、TL分别为所设置的空调可控温度的最高值、最低值），选择在可控温度范围内的空调组成可控开启群与关闭群参与调控；④进行功率响应，若集群功率需要减小，则优先关闭处于开启群中排名靠前的空调，若集群功率需要增加，则优先开启处于关闭群中排名靠前的空调。具体开启与关闭的空调数目由调控功率的大小决定。

然而当对集群中室温靠近Tmax或Tmin的空调进行启停控制（如关闭室温靠近Tmax的空调）时，经过较短的时间，这些空调将会因室内温度到达上下限而再次开启或关闭，从而导致设备频繁启停，危害使用寿命，同时也影响了控制效果。为避免上述问题，文献［15］设置了空调的可控温度TH与TL，并选择在室温可调控区［TL，Tmax］与［Tmin，TH］的空调参与控制，而在可调控区外的空调因其开启或关闭时间较短，不宜再次控制。通过设置可调控区，在一定程度上避免了部分空调频繁启停，但是当空调温度死区θ较小时，空调启停问题依然十分严峻。

为减小空调被控次数，本文在此基础上，进一步结合改变空调温度设定值的控制思想，提出了改进温度优先序列控制算法，如图2 所示。假设根据电网功率需求，在t1时刻关闭了某空调，则同时提高其温度设定值，并有ΔT1=Tin-Tmin；在t2时刻开启了某空调，则同时降低其温度设定值，并有ΔT2=Tmax-Tin，在温度调节过程中保持温度死区θ不变。经过上述处理，调控后的空调仍需要运行温度变化为θ的时间后才改变运行状态，从而避免了空调频繁启停。同时在对某一空调进行调控后，由于可控温度范围的约束，该空调在一段时间内将不再参与调控，从而避免了对空调的连续控制。该控制策略的流程图见附录A图A3。

图2 改进温度优先序列控制Fig.2 Improved temperature priority sequence control

上述控制策略改变了空调温度的设定值，在长时间下会对用户的舒适度造成一定的影响。基于此，本文设置了空调负荷闭锁约束：当某空调连续2次受控关闭并提高温度设定值后，对该空调实行闭锁操作，再次受控时仅允许降低该空调的温度设定值；同理，当某空调连续2 次受控开启并降低温度设定值后，再次受控时仅允许提高该空调的温度设定值，从而减小对用户舒适度的影响。

2 面向微电网功率波动平抑的空调负荷集群控制策略

2.1 空调负荷集群控制架构

用户侧空调负荷属于分散资源，相较于传统机组，单个空调负荷调控容量较小，因此，需要一个负荷控制中心将各分散空调整合，实现空调负荷集群与电网的交互。在电力市场环境下，负荷聚合商可以充当这一角色。负荷聚合商能够实时检测电网状态信息，通过一定的控制策略调控空调负荷集群功率以满足电网的需求。

在微电网中，分布式电源功率波动会造成频率的变化，因此可通过频率下垂控制实现对电网功率波动的平抑。空调负荷集群控制架构如附录A 图A4 所示，负荷聚合商实时监测各空调负荷的状态信息，包括负荷功率、室内温度及启停状态等，在检测到电网频率偏差信号后，根据集群控制策略，对群内空调的开关状态进行调控，从而实现集群功率的实时响应，满足电网的运行需求。

2.2 空调负荷集群控制策略

在微电网中，空调负荷集群可通过频率下垂控制实现对功率波动的平抑。传统下垂控制策略是仿照同步发电机一次调频曲线，根据频率的变化来实时调整机组出力，维持功率平衡。对于空调负荷集群，下垂控制策略如式（7）所示。

式中：P*为空调负荷集群目标功率，单位为kW；P0为集群初始功率，单位为kW；kf为频率下垂系数，单位为kW／Hz；f、fN分别为电网的实时测量频率和额定频率，单位为Hz。

然而，在电网中由于线路阻抗的存在，在对负荷进行调控时，负荷功率的改变会导致电压的变化，进而对调控效果以及电网的安全性造成影响，仅通过传统下垂控制无法满足电网控制需求，因此本文对下垂控制进行了改进。图3 为简单电力系统等值电路。设负荷节点电压为V∠0°；E∠δ为电源电压，δ为功角；Z为线路等值阻抗；R与X分别为线路等值电阻与电抗；I∠-φ为线路电流。

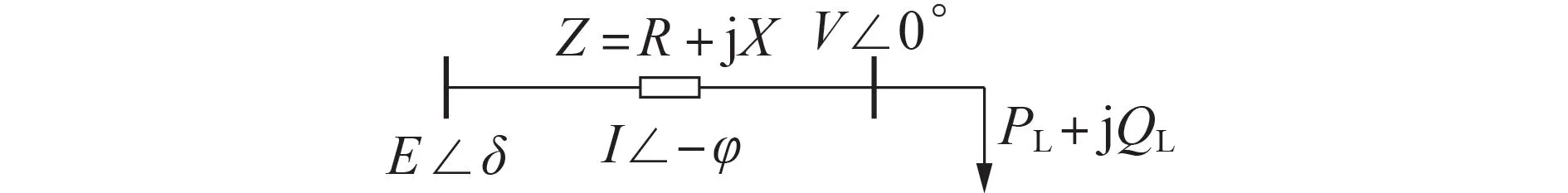
图3 电力系统等值电路Fig.3 Equivalent circuit of power system

根据潮流方程可得负荷有功功率PL及无功功率QL为：

因此，系统的电压降落受负荷功率以及线路阻抗的影响。根据空调负荷的电气模型，相较于通过换流器控制的其他可控资源，空调负荷的有功功率与无功功率无法解耦，负荷聚合商在调控集群有功功率时，会不可避免改变其无功功率［13］。由式（10）可知，当对空调负荷集群进行控制时，集群有功、无功功率的变化会导致负荷节点电压的改变［22］。同时根据空调负荷的ZIP 模型，其实际消耗的功率与负荷电压大小有关，当电压发生变化时，空调实际有功功率会偏离其额定值，从而使得集群实际响应功率偏离目标功率，具体过程如图4所示。

图4 响应功率偏差Fig.4 Deviation of response power

由图4 可知，空调负荷集群运行在点A，当电源出力增加时，系统频率上升，负荷聚合商按下垂曲线增加集群功率，最终系统在点B达到功率平衡。然而集群功率增加，导致负荷电压下降，进而使得每台空调的实际运行功率小于额定功率，集群实际运行在点C，响应功率小于目标功率。因此，本文对开关空调的数目进行实时调整，通过实时监测各空调负荷的功率，调整开关空调的数量，以消除响应功率的偏差。假设各空调负荷的ZIP 模型参数相同，在某一时刻开关空调的数目由式（11）决定。

式中：P*为当前各空调的有功功率，单位为kW；ΔN为当前时刻需要启停空调的数目。

由式（10）可知，系统的电压降落受负荷功率的影响，当空调负荷集群功率变化过大时，可能会导致负荷节点电压超过安全限值，给电网的安全运行带来威胁。根据式（10），可以得到负荷节点电压变化方程为：

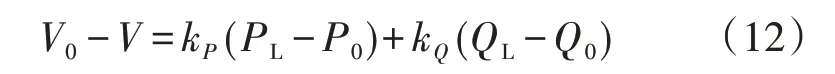
式中：V0为负荷节点初始电压，单位为V；Q0为空调负荷集群无功功率初始值，单位为kvar；kP与kQ为电压变化系数，kP=R/V，kQ=X/V。

为避免负荷节点电压越限，将式（12）引入电压约束，如式（13）所示。

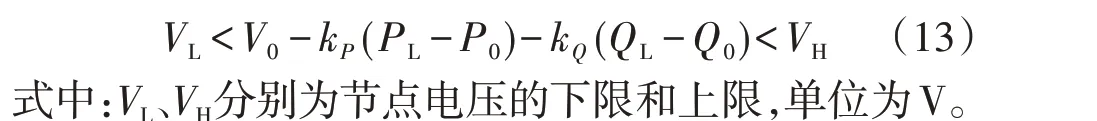
根据空调负荷集群群内控制策略，集群可控容量由处于可调节区的空调数目决定。为表征空调负荷集群的容量状态，定义空调负荷集群的等效荷电状态λSOC为：

式中：Δf=f-fN为电网频率变化量。

当集群可调容量充足时，下垂系数较大，以充分发挥其调节作用；而当集群可调容量较少时，下垂系数较小，以避免目标功率超出集群调节范围。

上述空调负荷集群控制策略能够实时平衡功率波动，使系统频率维持在一定范围内，保障了电网的安全运行。然而频率下垂控制为有差控制，在控制结束后，电网频率与额定频率仍然存在偏差，不利于电网稳定运行，因此需要构建频率辅助控制环节使之恢复到额定值。常用的方法为积差调频法，该控制策略的表达式为：

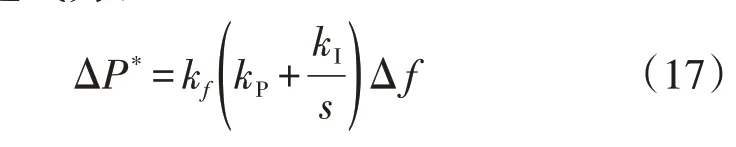
式中：kP、kI分别为比例系数和积分系数。根据式（17），当t→∞时，s→0，Δf→0，从而保证系统频率恢复到额定值。

需要说明的是，系统频率的恢复速度主要由积分系数的大小决定。本文将频率辅助控制环节与变下垂系数控制环节串联，当集群可控容量充足时，kf较大，则控制系统的等效积分系数较大，在调控过程中空调负荷集群功率变化较快，电网频率恢复也较快，当集群可控容量较小时，集群的控制效果同理，从而满足变下垂系数控制策略的控制需求。

然而，在实际情况下，电网的频率经常发生微小波动，为避免在微小频率波动下对空调负荷集群的频繁调控，本文进一步设置了频率调节死区：

-fh≤Δf≤fh（18）

式中：fh为频率调节死区限值。综上所述，空调负荷集群控制策略见附录A图A6。

3 仿真算例与分析

3.1 算例场景说明

为验证所提空调负荷集群控制策略的有效性，仿照IEEE 4 节点网络结构，在MATLAB／Simulink上搭建了如图5所示的微电网仿真模型。

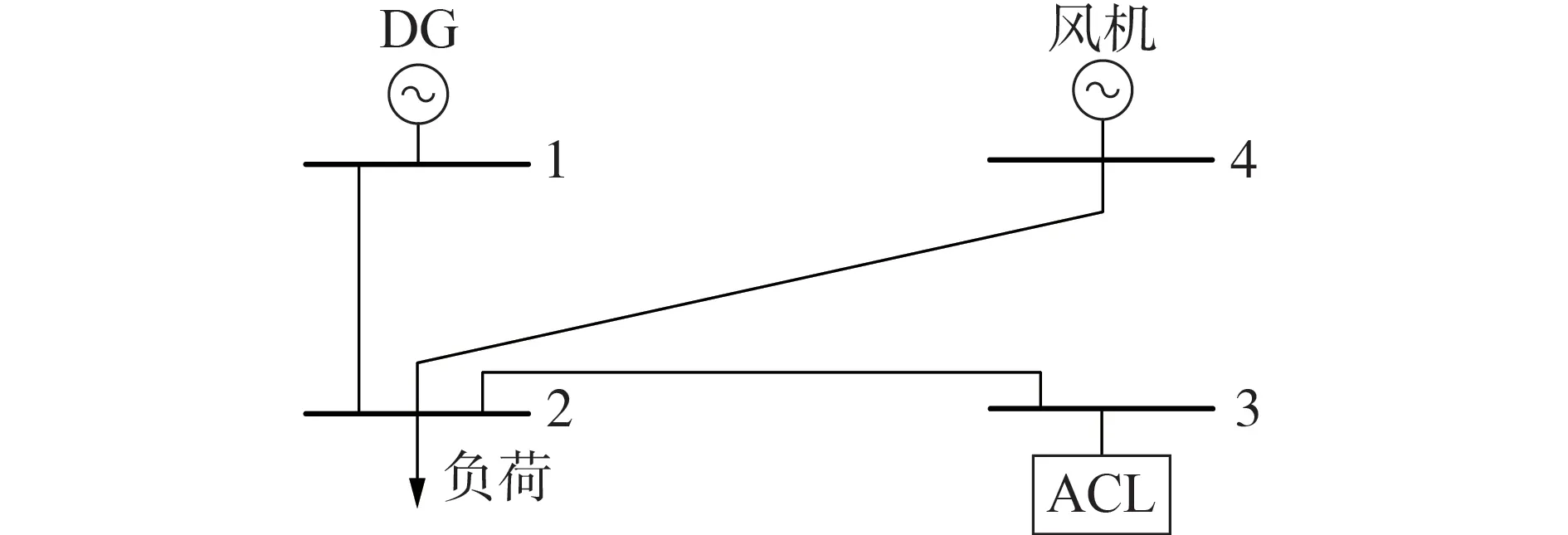
图5 仿真系统结构图Fig.5 Structure diagram of simulation system

取夏季某区域空调负荷集群作为研究对象，风机容量设置为275 kV·A，出力受风速影响；DG 容量为300 kV·A，采用下垂控制，下垂系数k*0=1；典型空调房间参数如附录A 表A1 所示，可控温度上、下限分别设置为TH=Tmax-0.2θ、TL=Tmin+0.2θ，空调负荷ZIP 模型参数如附录A 表A2 所示，额定有功功率为1 kW，无功功率为200 var，比例系数与积分系数分别设置为k*P=1、k*I=0.2；频率调节死区限值fh为0.01 Hz；系统网络参数见附录A表A3。

3.2 仿真分析

为了验证空调负荷集群控制策略的效果，本文设置了如下2 个算例场景：①微电网短时突增负荷；②微电网长期功率波动。

3.2.1 微电网突增负荷时空调负荷集群控制效果

设定在150 s 时微电网中负荷功率分别突增50 kW与100 kW，系统仿真结果如图6所示。

图6 负荷突增时微电网仿真结果Fig.6 Simulative results of microgrid during sudden load increase

当负荷功率突增50 kW 时，系统发电侧功率不足，频率下降，在频率下垂控制策略下，空调负荷集群功率逐渐减小。当系统达到稳定时，由图6 所示空调负荷集群功率变化曲线可知，空调负荷集群有功功率降低了40 kW，无功功率降低了7 kvar。按额定功率计算应关闭40 台空调，但由于此时节点3 电压升高，根据空调负荷ZIP 模型，各空调实际运行功率大于额定功率，根据功率偏差调整环节，实际关闭空调的数量为44 台，从而消除了由电压变化带来的集群响应功率偏差。根据图6 所示频率与节点3 电压变化曲线，在频率辅助控制环节的作用下，系统频率先突降到49.86 Hz 后逐渐恢复，经过15 s 后，频率基本恢复至50 Hz，保障了系统稳定运行；同时，由于集群功率降低，节点3 电压（线电压）上升了约12 V，在安全电压范围内。

当负荷功率突增100 kW 时，基于空调负荷集群控制策略，当系统功率达到平衡时，空调负荷集群有功功率应降低90 kW 左右。然而由于集群有功功率与无功功率变化过大，节点3电压上升至405 V，超过安全电压限值，给系统运行带来风险。通过式（13）所示的电压约束，当系统稳定时，节点3 电压被约束至最大值400.5 V，避免超出安全电压范围，而此时由于集群调控功率受到电压约束的限制，空调负荷集群功率降低了80 kW，无功功率降低了11 kvar，系统功率由空调负荷集群与DG共同平衡。由图6所示频率变化曲线可知，系统频率先突降到49.68 Hz后逐渐恢复，稳定时频率恢复到49.97 Hz，基本恢复至额定值。因此，当系统发生功率突变时，通过空调负荷集群控制策略，空调负荷集群能够及时维持系统的功率平衡，同时避免了负荷电压越限，保证了系统频率的快速恢复。

3.2.2 微电网功率波动时空调负荷集群控制效果

图7 为一天内室外温度变化与系统连续风电波动情况，所对应的微电网仿真结果如图8 所示（节点电压为标幺值）。

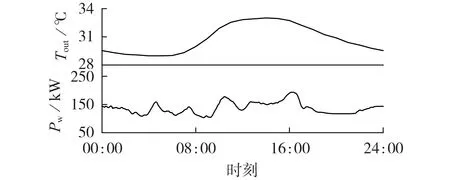
图7 室外温度及风电出力曲线Fig.7 Curves of outdoor temperature and wind power output

图8 风电功率波动时微电网仿真结果Fig.8 Simulative results of microgrid when wind power fluctuates

由图8中空调负荷集群功率变化曲线可知，基于空调负荷集群控制策略，空调负荷集群能够实时跟踪风电出力的变化，维持系统的稳定。同时，相较于有功功率的变化，空调负荷集群无功功率变化幅度较小，其原因是空调负荷的无功功率受电压的影响较大，从而在一定程度上减小了启停空调所带来的无功变化。在04:00 时开启一定数量的空调以增加集群有功功率，相应地其无功功率也会增加，而随着集群功率的增加，节点3 电压下降，使得每台空调的实际消耗的无功功率降低，因此集群无功变化较小。

根据图8中电网频率变化对比曲线，仅采用频率下垂控制时，系统频率最高超过50.1 Hz，而在加入频率辅助控制后，频率变化大幅降低，限制在±0.05 Hz内，极大地提高了系统的稳定性。由图8 中节点电压变化对比曲线可知，节点3（末端节点）电压变化幅度较节点2 大，同时在电压约束下，节点3 电压被限制在安全电压范围内，避免了电压越限给电网运行带来安全隐患。

图9 为在集群控制过程中，集群等效荷电状态（SOC）的变化情况。根据空调群内控制策略，在对空调负荷集群进行调控后，集群中最大可开启与关闭的空调数目在不断变化，因此集群等效荷电状态的最大与最小值也呈现出动态变化的特征。通过变下垂系数控制，当集群等效荷电状态靠近上下限时，集群响应功率变化相对较小，避免功率超出集群调控范围。

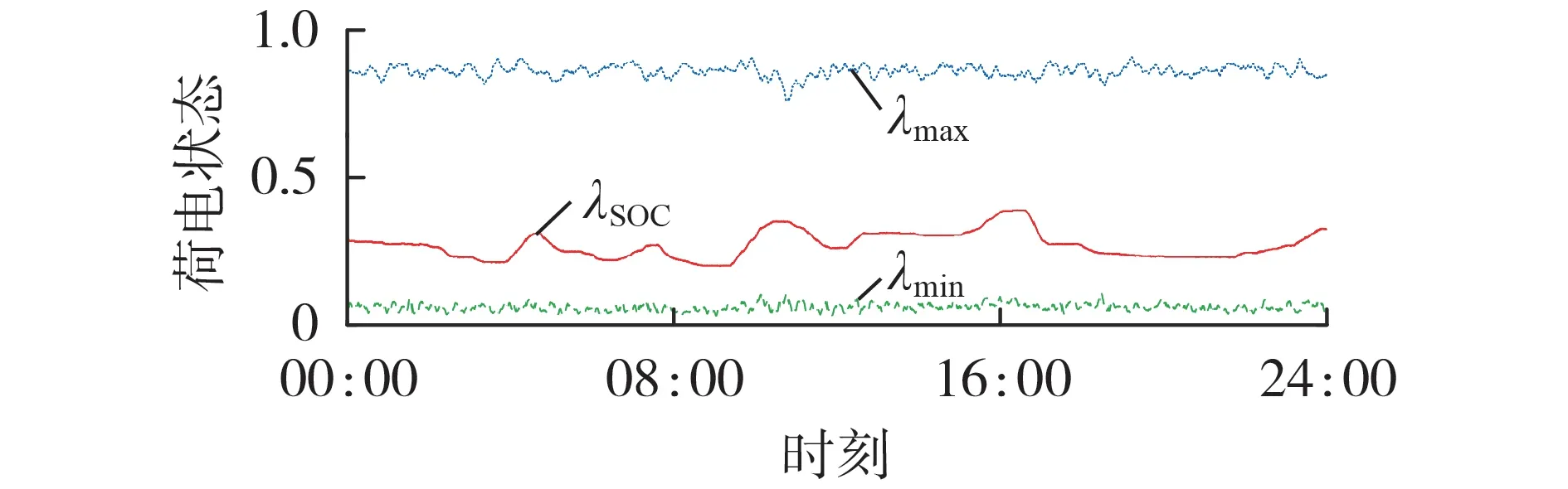
图9 空调负荷集群等效荷电状态变化Fig.9 Changes of equivalent SOC of air conditioning cluster

在空调负荷集群调控过程中，基于本文的改进温度优先序列控制策略，空调负荷集群的总受控启停次数为12 809 次，相较于文献［15］的控制策略减小了4405次，从而在一定程度上减小了对空调使用寿命的影响。附录A 图A7 展示了［00:00，04:00］时段中，400 台空调室内温度的变化曲线，可以看出通过设置空调闭锁约束，各空调室内温度基本维持在23～26 ℃范围内，有效保证了用户舒适度需求。因此，改进温度优先序列控制策略在满足用户舒适度需求的同时，能够有效避免空调频繁启停，减小对其使用寿命的影响。

4 结论

本文建立了空调负荷的热力学模型与电气模型，针对空调负荷集群群内，提出了改进温度优先序列控制策略；对于空调负荷集群整体，提出了一种基于下垂控制的空调负荷集群策略。仿真算例证明了本文控制策略的有效性，得出以下结论：

1）所提出的改进温度优先序列控制策略在保障用户舒适度的同时，降低了空调的启停次数，减小了对空调使用寿命的影响；

2）分析了在调控过程中空调负荷电压变化对集群响应功率的影响，通过实时检测各空调负荷功率，修正功率响应偏差，有效改善了集群控制效果；

3）采用本文所提出的空调负荷集群控制策略，能够实时平抑风电引起的功率波动，提升了电网运行频率的稳定性。

受用户使用行为的影响，空调负荷的运行状态具有一定的随机性，计及用户响应行为不确定性的空调负荷与电网的动态交互问题将是后续研究的重点。

附录见本刊网络版（http：//www.epae.cn）。