基于改进教与学优化的光伏阵列模型参数辨识研究
丁 晓,郑文明,岳 立,刘啸瑜,许一川,张峰毓
(1.国网江苏省电力有限公司,南京 210024;2.国网江苏省电力有限公司 常州供电分公司,江苏 常州 213003)
0 引言
能源问题是21世纪人类社会面临的重大课题,传统化石能源不可再生,且其带来较严重的环境问题,不符合清洁低碳、安全高效的能源发展趋势,因而太阳能、风能、水能等绿色可再生能源成为研究热点。随着我国能源结构的转型,可再生能源占比不断升高,能源有效消纳问题日渐突出。多能源互补综合能源系统能够实现各种能源协调优化,提高能源开发和利用效率,降低用能成本,有效解决能源问题。其中,太阳能作为可再生能源,在综合能源系统中占有重要席位。因此,光伏阵列作为光伏发电系统的重要组成部分之一,其模型以及工作参数的准确性对于故障诊断[1]、最大功率点跟踪[2]、发电功率预测[3]以及光伏发电系统并网运行稳定性评估[4]有着至关重要的意义。
光伏阵列模型可分为单二极管模型[5]、双二极管模型[6]和三二极管模型[7]。单二极管模型和双二极管模型能够在精确表征光伏模型的同时,兼顾模型简单性和参数提取迭代速度,因而应用最为广泛。文献[8]提出一种三参数单二极管模型,为了避免迭代过程忽略串联电阻和并联电阻,以牺牲精度为代价直接求解光伏模型。文献[9]提出一种四参数单二极管模型,忽略并联电阻的影响,可以得到较高精度的光伏模型,但由于并联电阻对阵列功率消耗有重要影响,因此其适用性较低。文献[10]考虑并联电阻和串联电阻的影响,提出一种五参数单二极管模型,该模型计算出的电流与实测电流相对误差控制在6%以内,能够精确表征光伏模型。文献[11]提出一种五参数双二极管模型,以短路、开路以及最大功率点这3个关键点对模型参数进行迭代求解,该模型仿真结果与实测数据的归一化均方根误差在7%以下,在温度与辐照度较高时误差接近7%。文献[12]提出一种双二极管七参数模型,在高温与低辐照度下精度高,功率误差控制在3%以内。文献[13]对比了单二极管五参数模型与双二极管七参数模型,双二极管模型虽然更精确,但由于未知参数更多,方程更复杂,因此需要在模型精度与代价之间平衡。
光伏阵列模型参数辨识方法主要有解析法和数值法[14]。解析法对求解模型要求较高,但由于光伏阵列模型参数关联性强,导致求解过程复杂、求解精度不高。数值方法虽不能求解得到精确解,但若控制求解精度,则可得到满足使用需求的数值解,因此越来越多的研究趋向于使用数值法对光伏阵列模型参数进行辨识。传统数值方法有牛顿法、雅可比法、高斯-赛德尔迭代法等。文献[15]采用牛顿迭代法对光伏阵列双二极管模型进行参数辨识,仿真数据与实测数据均方根误差为0.08。文献[16]提出一种高斯-赛德尔迭代法用于提取光伏模型参数,整体上仿真数据接近实测数据,但在最大功率点附近,实测数据与仿真数据差异较大。由于传统方法对迭代初值敏感且容易陷入局部最优,因此其在光伏阵列模型的参数辨识应用上并不广泛。近年来随着人工智能的发展,各种元启发式算法被用于光伏阵列模型参数辨识。元启发式算法的核心为尽可能搜索整个空间并充分利用有效信息,因此能够快速收敛于全局最优。文献[17]提出一种混合遗传算法对光伏模型参数进行辨识,通过染色体交叉实现算法收敛于全局最优值,通过基因变异来跳出局部最优,但该方法在进化后期搜索效率低,迭代至收敛所需次数较多。文献[18]提出一种改进人工鱼群算法,通过鱼群觅食、聚群、追尾和随机行为来搜索全局最优值,该算法辨识精度高,但收敛速度较慢,且较难避免陷入局部最优。
为快速、高效、准确地建立光伏电站中阵列电气特性数学模型,本文基于单二极管五参数模型提出一种改进教与学优化算法,对模型参数进行辨识。该算法初始化参数少、局部搜索能力强、迭代次数少,在模型参数辨识上具有较好的适应性和实用性。然后将辨识的参数回代到模型中,对比分析模型仿真数据与实测数据,验证了该光伏阵列模型的准确性,为下阶段综合能源系统建模奠定模型基础。
1 光伏阵列数学模型
光伏阵列是由若干数量的光伏电池串并联构成的,因此其数学模型可以通过光伏电池模型叠加求得。由于单二极管五参数模型相对简单、求解参数少、精度高、应用广泛,因此本文采用单二极管五参数模型描述光伏电池I⁃V特性,并基于单二极管光伏电池模型对光伏阵列进行建模。
1.1 光伏电池模型
光伏电池单二极管模型如图1所示[19],根据基尔霍夫电流定律可得

图1 光伏电池单二极管模型等效电路Fig.1 Equivalent circuit model of PV cell single diode

式中:IL为输出电流;Iph为光生电流;ID为等效二极管电流;Ish为并联电阻电流。
根据肖克莱方程可求得等效二极管电流ID,如式(2)所示[20]。根据基尔霍夫电压定律可计算得并联电阻电流Ish,如下所示

式中:Is为二极管反向饱和电流;q为元电荷,q=1.60×10-19C;UL为输出电压;Rs为串联电阻;n为二极管理想因子;k为玻尔兹曼常数,k=1.38×10-23J/K;T为光伏电池工作下的热力学温度;Rsh为并联电阻。
将式(2)、式(3)代入式(1)可得其等效电路数学模型,如下所示
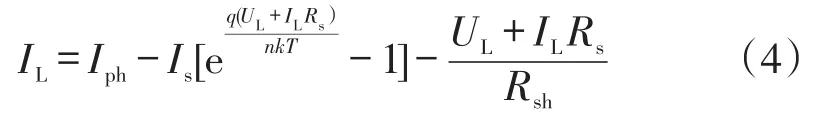
1.2 光伏阵列模型
光伏阵列等效电路模型可由光伏电池模型叠加求得,该等效电路模型如图2所示。其由Ns个光伏电池串联构成一个串联子串,并由Np个串联子串并联构成。光伏阵列单二极管数学模型如下所示
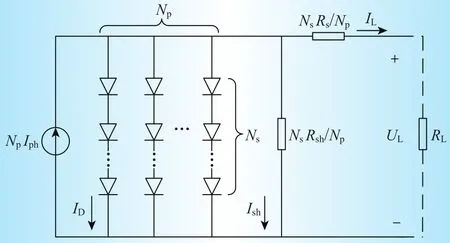
图2 光伏阵列等效电路模型Fig.2 Equivalent circuit model of PV array
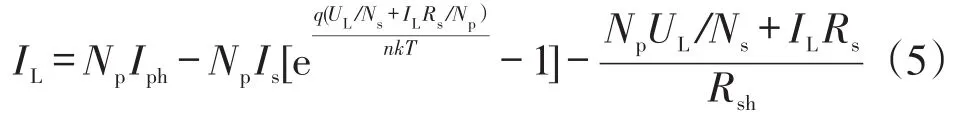
光伏阵列数学模型主要参数有等效光生电流NpIph,等效反向饱和电流NpIs,二极管理想因子n,等效串联电阻NsRs/Np,等效并联电阻NsRsh/Np。为简化模型,将带入式(5)中,可得光伏阵列数学模型,如下所示
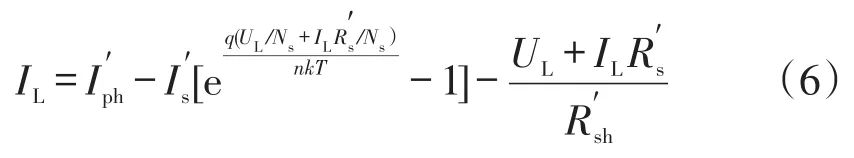
2 教与学优化算法
教与学优化(teaching learning⁃based optimiza⁃tion,TLBO)算法[21]是一种基于种群的启发式算法。该算法模拟老师与学生之间的教学与学习过程,以提高学生总体水平,使得全部学生趋向并收敛于最优解。
TLBO算法可分为教学阶段和学习阶段,在这两个阶段前需要对班级学员初始化。为保证初始学生具有随机性与多样性,班级成员初始化如下所示

式中:rand为随机数,取值范围为[0,1];xmax和xmin分别为学员x能取到的最大值和最小值;xi为第i个学生的值。
教学阶段取班级最优学生为教师,所有学生向教师学习,如下所示[22]
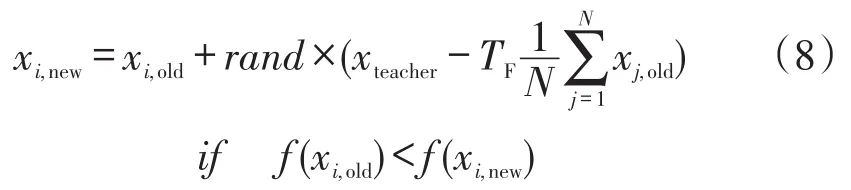
式中:xi,new为第i个学生新值;xi,old为第i个学生旧值;xteacher为所有学生中水平最优的学生;TF为教学因子,TF=round(1+rand),round为取整;N为学生总数;f(xi)为第i个学生的水平,即适应度值。
学习阶段班级学生相互学习,如下所示[23]
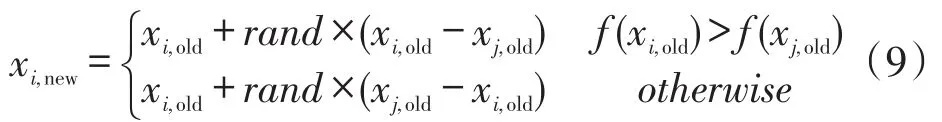
TLBO算法是一种在求解域搜索最优值的寻优算法,即寻求函数f(x)在定义域内取得最优解对应的x值。初始化班级学员x1,x2,…,xN后,对学生进行评价,记录班级最优值f(xi),再通过学生向教师的学习和学生之间相互学习来改善学生水平,即通过式(7)和式(8)迭代更新学生x1,x2,…,xN的值并在求解域内搜索最优值,直到所有学生水平都达到最优,即所有学生都收敛于x,从而得到最优解x。由于该算法采用全体向最优学习和随机个体相互学习更新学生且所需参数较少,相较于其他算法在保证算法精度较高的同时拥有较快的迭代速度。
3 基于改进TLBO算法的光伏阵列模型参数辨识
3.1 目标函数的建立
光伏阵列参数辨识是将阵列实测电流-电压数据代入光伏阵列数学模型,寻求使得模型仿真结果与实测数据差距最小时的参数值,因而可将光伏模型参数辨识问题转化为优化问题。以光伏阵列等效电路模型式(6)计算的电流值和实测电流值间的均方根误差(root mean square error,RMSE)作为目标函数,模型参数辨识为在求解域内寻求目标函数RMSE最小值过程,如下所示

式中:N为实测样本点数量;IL、UL为光伏阵列实测输出电流、输出电压值;x为光伏阵列等效光生电流、等效反向饱和电流、二极管理想因子、等效串联电阻和等效并联电阻构成的向量,x=[Iph,Is,n,Rs,Rsh]。
3.2 基于改进Tent混沌映射的辨识参数初始化
为提高TLBO算法的全局搜索能力,引入改进Tent混沌映射以替代随机数对待辨识参数构成的向量x=[Iph,Is,n,Rs,Rsh]进行初始化,使得x1,x2,…,xN在求解域分布均匀且具有多样性,以获得更优的遍历搜索性能。
基于改进Tent混沌映射的待辨识模型参数xi初始化如下所示
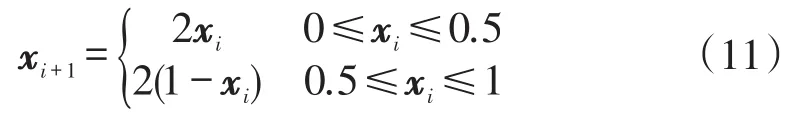
由于求解得到的x1,x2,…,xN为各个分量,取值范围均为(0,1),因此需要对其各个分量反归一化使其映射到求解空间,得到初始化模型参数向量组x1,x2,…,xN。
3.3 基于扰动机制的早熟解决策略
由于TLBO算法在多维度空间搜索可能陷入局部最优,因此需要判断算法是否停滞于局部最优,并增加扰动机制,在算法早熟时增加扰动使其跳出局部最优。
本文采用适应度值即目标函数值RMSE(xi)的方差σ2作为早熟判断标准,如下所示

式中:E(RMSE)为适应度值均值,若算法早熟陷入局部最优,则迭代计算的σ2与其前几次迭代计算的σ2差异较小,且当前最优适应度值劣于理论最优适应度值。
当算法陷入早熟时,需引入扰动以打破收敛状态,使其在求解空间再次进行搜索。本文改进Tent混沌映射,通过式(11)进行0.5N次迭代产生混沌序列,并计算该混沌序列反归一化后的适应度值,取其最优适应度值对应的混沌数,计算其反归一化值替代原光伏阵列辨识参数向量组x1,x2,…,xN中最劣适应度值的对应向量,得到新的向量组进行迭代求解。
3.4 改进TLBO算法流程
Step1:根据式(6)建立光伏阵列模型,确定待辨识参数向量x=[Iph,Is,n,Rs,Rsh],并根据式(9)构建目标函数RMSE。
Step2:改进Tent混沌映射迭代N-1次并反归一化后得到待辨识模型参数的初始化向量组x1,x2,…,xN。
Step3:计算每个向量对应的适应度值,选取适应度值最优对应的向量xi作为xteacher。
Step4:向量组x1,x2,…,xN中除xteacher外的每一个向量xi通过式(7)向xteacher学习,得到更新的x1,x2,…,xN。
Step5:向量组x1,x2,…,xN中的任意一向量通过式(8)随机向其他向量学习,得到更新的x1,x2,…,xN。
Step6:通过式(11)计算目标函数值RMSE(xi)的方差σ2,若σ2与上次计算的σ2差值的绝对值即|Δσ2|较小,且当前最优适应度值RMSEmin劣于理论最优适应度值RMSEtv。则执行Step7,否则执行Step8。
Step7:通过式(10)进行0.5N次迭代产生混沌序列并计算该混沌序列反归一化后的适应度值,取其最优适应度值对应的混沌数,计算其反归一化值替代原光伏阵列辨识参数向量组x1,x2,…,xN中任意向量,得到新的向量组x1,x2,…,xN。
Step8:若达到迭代次数,输出辨识参数向量x,并终止。否则执行Step3。
算法流程如图3所示。
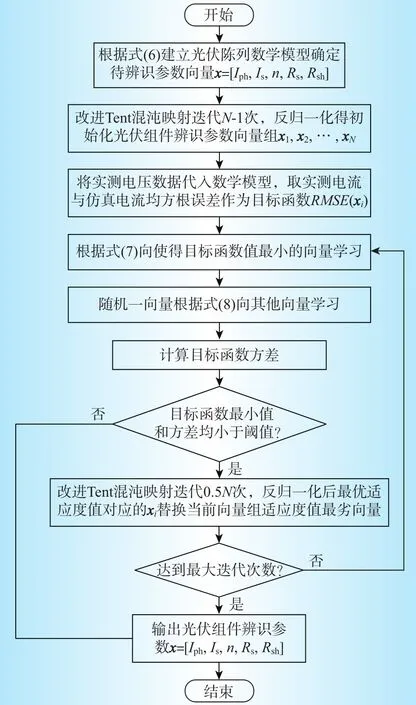
图3 改进TLBO算法流程Fig.3 Improved TLBO algorithm flow
3.5 光伏阵列模型求解
将辨识结果x=[Iph,Is,n,Rs,Rsh]代入式(6)得到光伏阵列模型,并令IL=0,得到式(13)如下

式(13)为关于UL的隐式方程,难以通过令IL=0求解开路电压Voc,因此采用史蒂芬森迭加速代[24]计算开路电压Voc,史蒂芬森加速迭代公式如下所示

式中:yj=φ(xj);zj=φ(yj)。
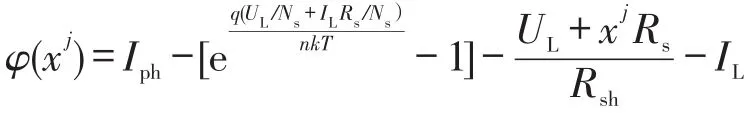
4 光伏阵列参数辨识结果与分析
为验证光伏阵列模型的准确性以及改进TLBO算法在光伏阵列参数辨识的可行性与准确性,本文采用光伏电站22个光伏组件串联而成的光伏阵列实测数据进行验证。光伏组件参数如表1所示。

表1 TSM⁃240组件电气参数Table 1 Electrical parameters of TSM⁃240
为验证改进TLBO算法在光伏阵列参数辨识的准确性和稳定性,对不同辐照度下的电压电流数据分别进行30次参数辨识,求取目标函数RMSE的最大值、最小值、均值及标准差,结果如表2所示。由表2可知,改进TLBO算法求解的目标函数RMSE量级为10-2,RMSE理论值为0,误差在百分位,表明该算法寻优准确性较高。进行30次辨识求得RMSE标准差量级在10-5,表明该算法有较好的寻优稳定性。

表2 不同辐照度下目标函数RMSETable 2 Objective functionRMSEunder different irradiances
为进一步验证改进TLBO算法在不同辐照度下寻优性能,对不同辐照度下的1 000组数据进行参数辨识,求取目标函数值RMSE,并进行多项式拟合,拟合结果如图4所示。由图4可知该算法在参数辨识过程中,随着辐照度增加,目标函数值RMSE先降低后升高,即辨识结果准确性先升高后下降,在辐照度为300 W/m2下寻优结果最为准确。

图4 不同辐照度下目标函数RMSE拟合曲线Fig.4 Fitting curve of objective functionRMSEunder different irradiances
为验证改进TLBO算法在光伏阵列参数辨识的快速性,对不同辐照度下求取目标函数最小值收敛过程绘制曲线,如图5所示。并统计其在Windows 10系统中,处理器为R7⁃5800H,MATLAB环境下参数辨识结果和所需时间,如表3所示。由图5和表3可知,改进TLBO算法在迭代150次以内已经收敛,且该算法在参数辨识过程耗时较短,平均耗时为1.193 s。

表3 不同辐照度下光伏阵列参数辨识结果Table 3 Identification results of photovoltaic array parameters under different irradiances

图5 不同辐照度下迭代收敛过程Fig.5 Iterative convergence process under different irradiances
为进一步验证光伏阵列模型准确性和改进TLBO算法参数辨识结果的准确性。在相同条件下对辐照度为908.4 W/m2,温度为56.86℃的实测数据采用不同元启发式算法进行模型仿真求解。不同辐照度下仿真电流-电压曲线如图6所示。
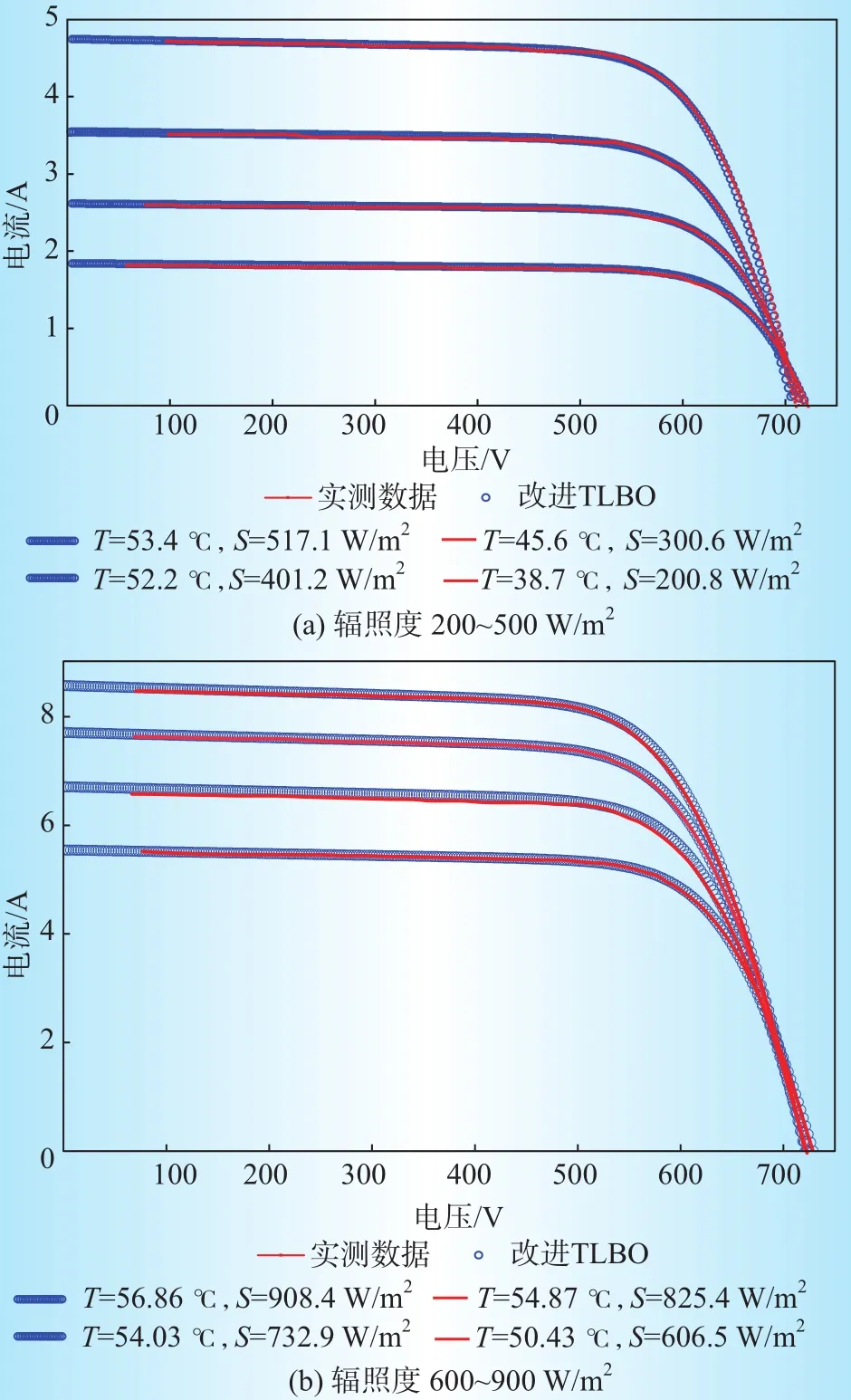
图6 不同辐照度下仿真电流-电压曲线Fig.6 Simulation ofI⁃Vcurves under different irradiances
图7为改进TLBO算法、遗传算法(genetic algorithm,GA)和花授粉算法(flower pollination algorithm,FPA)下的仿真电流-电压曲线与实测电流-电压曲线对比图。

图7 不同算法下仿真I⁃V曲线Fig.7 Simulation ofI⁃Vcurves with different algorithms
为更加准确地表明模型的准确性和算法的精确性、快速性,计算仿真数据与实测数据开路电压相对误差δV、短路电流相对误差δI、最大功率点相对误差δP,结果如表4所示。由表4可知,仿真结果与实测数据误差控制在1%以内,该光伏阵列模型准确性较高,改进TLBO算法在保证较高的精确度的条件下能够拥有较快的参数辨识速度。

表4 不同算法下模型仿真误差Table 4 Error of simulation results with different algorithms
5 结束语
本文建立光伏阵列数学模型,并提出一种基于改进TLBO算法的光伏阵列模型参数辨识方法。引入改进Tent混沌映射进行初始化,使得初始化参数分布随机且均匀。采用扰动机制,使得该算法具有较强的跳出局部搜索能力,以提高光伏阵列电气特性建模的准确性。通过光伏电站实测数据对该算法进行验证,验证结果表明,该模型准确性较高,且改进TLBO算法在光伏阵列模型参数辨识过程中具有较优的准确性、快速性和稳定性,为下阶段综合能源系统建模奠定模型基础。

