基于集合卡尔曼滤波与相空间重构的负荷预测方法研究

付文杰，李 化，杨伯青，宋 杰

（1.国网河北省电力有限公司 保定市供电分公司，河北 保定 071000；2.国电南瑞南京控制系统有限公司，南京 211100）

0 引言

电力负荷预测对电网调度的自动控制十分重要，随着能源互联网的发展及电力改革的推进，负荷预测的应用也逐步扩展到售电侧和用户侧［1—2］。准确的负荷预测不仅能够增加售电商的收益，而且可以改善用户侧需求响应的实施效果，对电网运行的稳定性和经济性都大有裨益［3］。

受到多重非线性因素的影响，电力负荷时间序列具有混沌性质，这使得利用混沌理论对其进行处理具有天然的适合性［4—5］。混沌预测是建立在重构电力负荷时间序列相空间基础上的，延迟坐标嵌入作为广泛应用的相空间重构方法，在使用时需要选取延迟时间和嵌入维数［6］。对于延迟时间的选取，通常用自相关系数法和互信息法，后者由于考虑了系统的非线性因素，因而性能更佳。嵌入维数的确定，常用几何不变量法、虚假最邻近点法和改进虚假最邻近点法。其中虚假最邻近点法对噪声比较敏感，且阈值的选取具有主观性。而改进虚假最邻近点法则不存在这些问题，只需要用到延迟时间和较小的数据量就可以确定嵌入维数［7—8］。本文所采用的实测数据来自智能电力终端采集的海量电力负荷数据，这些数据中往往包含许多采样噪声，这些噪声无疑会侵蚀负荷预测的精度。将随机滤波与相空间重构相结合，以便将噪声对时间序列预测结果的影响最小化，提升预测精度。常用的非线性随机滤波有扩展卡尔曼滤波、无迹卡尔曼滤波、集合卡尔曼滤波（ensembleKalman filter，EnKF）等［9］。其中，EnKF用一系列状态的采样值来近似系统的非线性，无需求解雅可比矩阵。当集合中采样点的数量远小于状态维数时，其时间复杂度小于扩展卡尔曼滤波。同时，EnKF对系统模型的要求较低，对模型偏差和不完整性的容忍度较高［10—11］。

本文使用数据驱动的方法对家庭分项电器负荷与总负荷进行短期预测。首先，由非侵入式量测终端获得的海量历史负荷数据组成一维时间序列。依据提出的基于集合卡尔曼滤波和相空间重构（reconstructing phase space，PSR）的组合模型（EnKF⁃PSR），应用延迟坐标嵌入法对该一维时间序列进行相空间重构。采用互信息法和改进虚假最邻近点法分别选取延迟时间和嵌入维数，并且采用局部平均法预测下一时刻的负荷。根据无迹变换理论，对负荷预测值选取合适数量的Sigma点组成预测值集合，并使用EnKF算法进行数据同化，最终得到经过随机滤波的分项电器负荷预测值和家庭总负荷预测值。本文的方法旨在优化负荷预测结果，减小数据采样噪声对预测结果的影响，具有较高的预测精度。

1 EnKF⁃PSR组合模型

1.1 传统的PSR模型

对于具有混沌性质的电力负荷时间序列，根据Takens嵌入定理，可以从该序列中重构一个与原动力系统在拓扑意义下一样的相空间［12］。由于对初始条件极其敏感，因此相空间重构方法往往用来进行短期预测。利用延迟坐标的方法重构相空间，关键在于延迟时间和嵌入维数两个参数的选取。

1.1.1 延迟时间

定义两个电力负荷的时间序列S、Q如式（1）所示，其中Q为S经过延时τ后所得

两个时间序列之间的互信息为延迟时间τ的函数，互信息I(τ)的大小代表在已知时间序列S的情况下，时间序列Q的确定性大小。可表示如下

式中：I(τ)的第一个极小值表示两个时间序列之间不相关的最大可能性，因此使用I(τ)的第一个极小值作为最终的延迟时间τ；H(S)、H(Q)和H(S,Q)分别为各自时间序列的信息熵及联合信息熵，如式（3）—式（5）所示

式中：P为相应的概率。

1.1.2 嵌入维数

基于电力负荷的时间序列S和延迟时间τ，可以构造相空间yi(d)如式（6）所示

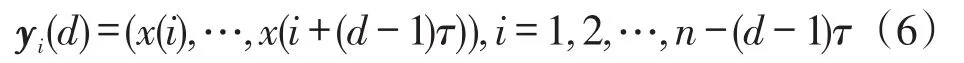
式中：d为嵌入维数。

所谓虚假临近点，是指高维相空间并不相邻的两个点投影到一维空间上，有的时候会成为相邻的两点。在d维相空间中，每个向量yi(d)都有一个最临近点。衡量两点之间距离的尺度可以是欧几里德距离|·||2或最大模范数||·||∞，本文使用后者。定义变量a(i,d)、E(d)、E1(d)如下所示

式中：a(i,d)为使得对应向量在最大模范数下离向量yi(d)最近；E(d)为在d维的范围内，对a(i,d)求取平均值；E1(d)为当维数从d变为d+1时，变量E(d)的变化程度。通过迭代计算，当维数d大于一定值dc，而E1(d)不再变化时，选取dc+1为时间序列的嵌入维数。

1.1.3 局部平均预测

依据选取的延迟时间和嵌入维数完成相空间重构，形成第i个向量yi如式（6）所示。因此，可以在d维欧式空间建立系统模型如下所示

式中：F为一个连续函数。令N=n-(d-1)τ，根据连续函数的性质，如果yN与yh很接近，则可用x(h+1)作为x(N+1)的近似。以最大模范数||·||∞为衡量标准，从相空间中选取k个与yN最接近的向量，根据局部平均预测思想可以得到电力负荷时间序列下一时刻的预测值x(n+1)如下所示

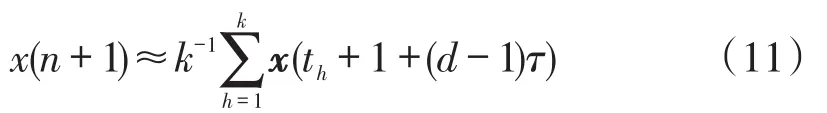
式中：th为第h个最接近的向量。

1.2 EnKF⁃PSR模型

基于传统PSR模型得到的负荷预测值中依然包含采样噪声和随机噪声。本节通过EnKF算法对负荷预测值进行分析与校正，EnKF算法将噪声纳入迭代计算中，容忍其存在的同时能够给出最优的负荷状态预测。

1.2.1 模型系统结构

EnKF-PSR组合模型的系统结构如图1虚线框中所示。模型对输入数据的处理过程主要分为以下3个阶段：

图1 模型系统结构图Fig.1 Structure diagram of model system

（1）PSR参数选取。基于电力负荷时间序列S，根据互信息I(τ)极小值法选取延迟时间τ；根据虚假临近点法选取嵌入维数d。参数选取完成后，相空间重构即可完成。

（2）无迹变换及PSR预测值集合形成。通过无迹变换方法得到相空间中各个变量的Sigma点集，再依据局部平均预测法得到PSR预测值集合。

（3）EnKF分析及校正。使用EnKF算法对PSR预测值集合进行分析和校正处理，最终得到负荷预测结果。

1.2.2 无迹变换与EnKF

电力负荷背后隐藏的动力系统是一个受多重因素影响的强非线性系统，可用式（12）所示的方程描述其动态规律和观测行为。庞大的电力负荷通常很难用准确的数学模型进行预测，因此本文采用数据驱动的方法。对应到式（12）中，主要考虑vk代表的量测噪声，即采样噪声。

式中：xk为状态变量；yk为观测值；wk、vk分别为代表模型噪声、量测噪声的白噪声过程。

在EnKF理论中，通过对系统在k时刻的状态进行有限次采样，组成一个状态集合，然后使用此集合来近似系统的非线性。鉴于电力负荷预测中，精确的非线性函数f和g未可知，因此考虑使用无迹变换的方法来创建描述状态xk的点集。假设随机变量xk的均值和协方差分别为xˉ和Pk，采取对称采样的策略选取2n+1（n为状态变量的维数）个Sigma点及其相关权重来表征xk，如式（13）所示。Sigma点和相关权重的选取原则如式（14）所示，其中上标为a的量代表预测值相关，上标为0的量代表均值相关，即Sigma点集的中心，其他所有点关于均值对称分布，且所有权重之和为1。

由于相空间中的向量反映系统状态，因此考虑如式（15）所示的k时刻d维观测延迟向量xk。

根据式（11）所示的局部平均预测法，可对点集中的每一个Sigma点进行处理，得到相应下一时刻的预测值。当预测部分完成后，结合k+1时刻的量测值yk+1。再根据式（16），即可对预测值进行校正，从而得到最优的预测结果。

式中：Kk为卡尔曼增益；为状态与观测的交叉协方差；为量测协方差；Pk为状态的协方差；为状态预测值；为观测预估值；Q、R分别为模型噪声的协方差和量测噪声的协方差，本文假定它们为零均值白噪声。

1.2.3 数据处理与算法流程

模型的输入数据源自非侵入式量测终端。非侵入式负荷辨识技术是一种新型高级量测技术，通过在用户关口安装终端、表等采集电力负荷输入总线的总电流、电压等实时信息，利用总电流、电压等包含的负荷特征信息和高级算法来实现负荷辨识。目前预测精度平均85%以上，其中300 W以上大功率电器识别率95%以上［13］。当前的非侵入式负荷辨识数据辨识精度可支撑电力供需互动的负荷预测，特别是家庭主要大功率电器。非侵入式负荷辨识细化了家庭电器负荷类型感知，能提升负荷预测精度。

由于人为因素或某些特殊原因，采样得到的负荷数据有时包含一些坏点。本文对采样数据进行预处理，基于最大熵算法［14］建立了坏点分类模型，如图2所示。

图2 基于最大熵的坏点分类模型Fig.2 Abnormal data classification model based on maximum entropy

基于EnKF⁃PSR组合模型的电力负荷预测算法流程如图3所示。在利用局部平均法预测下一时刻的状态时，对最临近向量的个数采取迭代的方式选取，从2个最邻近向量个数开始进行计算直至状态预测值收敛为止。这样处理可以根据不同的电力负荷数据训练集实时选取合适的最临近向量数目，具有自适应性，从而最优化算法执行时间。

图3 负荷预测算法流程Fig.3 Load forecasting algorithm flow

2 案例分析

2.1 预测误差评价指标

在电力负荷的预测过程中，由于数学模型的简化、各种影响因子的忽略、不当的参数选取、训练样本不完整等因素，导致预测值与真实值之间一般总有误差。一种简单的评价指标是绝对误差，即负荷预测值与真实值之间的差值。但是，这种评价指标对误差大小的表达不够直观。本文使用相对误差来作为评价指标，更加直观。假设y(i)和ŷ(i)分别是i时刻的负荷真实值和预测值，则它们之间的相对误差如式（17）所示

2.2 样本数据

样本数据来自基于图2所示的非侵入式终端量测得到的河北省保定市50个家庭用户的2019年7月10日到7月15日的用电数据，包括电热水器、空调的负荷以及家庭总负荷，采样间隔为15 min。表1给出了所采集的样本数据，为50个家庭的负荷数据总和。

表1 样本数据Table 1 Sample data

对于一维电力负荷时间序列，对每一个状态选取3个Sigma点组成点集。中心点的权重W0取0.5，另外两点的权重W1、W2均取0.25。表1中电热水器SWH、空调SAC和总负荷STOTAL的时间序列可分别表示如下：

根据式（1）—式（5）求出相关概率后再利用互信息I(τ)极小值法求出延迟时间。根据式（7）—式（9）求取嵌入维数。算法中的主要参数如表2所示。

表2 算法主要参数Table 2 Main parameters for algorithm

由于本文的主要工作是初步验证所提算法对电力负荷预测的可行性和有效性，因此，延迟时间与嵌入维数的选取并不是最优的。在下一步开展的工作中，需要对比多组延迟时间和嵌入维数对符合预测效果的影响，以优化参数选取。

2.3 实验结果

基于EnKF⁃PSR组合模型算法分别得到热水器、空调和家庭总负荷的预测值。图4给出了一天中电热水器负荷的预测值、实际值和相对误差。

图4 电热水器负荷预测效果Fig.4 Forecasting effect of electrical water heater load

由图4可以看出，误差范围主要集中在+7～-10之间，预测效果令人满意。通过电热水器的负荷预测结果可以得知，用户对电器的主要使用时段集中在21:00—23:00，这也符合多数用户工作和休息时段的实际情况，再次说明预测结果能够较为准确的反应真实的用户行为。

图5给出了一天中空调负荷的预测值、实际值和相对误差。误差范围主要集中在-15%～+15%之间，预测效果比较令人满意。根据式（17）所示的相对误差计算方法，由图2、图3可以看出，相对误差的大小不仅取决于绝对误差，还同时受到公式中的分母即负荷实际值大小的影响。由于空调的使用受个人习惯、家庭经济状况等众多因素影响，因此随机性较大，故预测误差相对较大。通过空调的负荷预测结果可以得知，用户对电器的主要使用时段集中在12:00—15:00以及21:00—23:00。由于本文采集的数据归属于夏季，因此预测结果符合多数用户工作和休息时段的实际情况，再次说明预测结果能够较为准确的反应真实的用户行为。

图5 空调负荷预测效果Fig.5 Forecasting effect of air⁃conditioner load

图6为基于EnKF⁃PSR模型的总负荷预测值与实际值的比较以及相对误差。误差范围为-10%～+10%，取得了较好的预测效果。总负荷的变化趋势符合夏季用户侧负荷的实际变化规律。同时，将单纯基于PSR模型的预测结果与实际值作比较，相对误差如图7所示，误差范围为-11%～+22%。由于采样噪声的存在，使得负荷预测结果与实际值之间存在较大的偏差。对比图6和图7可以看出，EnKF⁃PSR组合模型预测方法能够在存在采样噪声的情况下给出更为优化的负荷预测结果，因此具有更好的预测效果。

图6 基于EnKF⁃PSR模型时总负荷预测效果Fig.6 Forecasting effect of total power load based on EnKF⁃PSR model

图7 基于传统PSR模型时总负荷预测效果Fig.7 Forecasting effect of total power load based on traditional PSR model

3 结束语

本文基于提出的EnKF⁃PSR组合模型对家用分项电器和家庭总负荷进行短期预测。在存在采样噪声的情况下，使用EnKF算法对负荷预测值进行分析和校正，给出最优负荷估计。通过非侵入式终端获取河北保定50个家庭用户的历史用电数据进行样本训练，从而得出算法所需的延迟时间、嵌入维数等主要参数。实验结果表明，与传统PSR方法相比，本文提出的EnKF⁃PSR组合模型方法具有更好的负荷预测效果。下一步的工作重点在于对比不同延迟时间和嵌入维数对负荷预测效果的影响，以期得到优化的延迟实际和嵌入维数以及更佳的负荷预测效果。