质子辐照对RADFETs的γ辐照剂量响应的影响研究

马 函孙 静何承发荀明珠

1（中国科学院新疆理化技术研究所乌鲁木齐830011）

2（中国科学院大学北京100049）

辐射敏感晶体管（Radiation Sensitive Field-Effect Transistors，RADFETs）是基于辐射导致P沟道金属氧化物半导体（Positive channel Metal Oxide Semiconductor，PMOS）氧化层陷阱电荷变化的一种剂量计，也被称为PMOS剂量计，最早由Holmes-Siedle提出［1］。经多年的发展，由于其较好的线性度、体积重量小、使用便利等特点，RADFETs已被广泛应用于空间科学、放射医学、核工业等各种场景［2-5］。

RADFETs在使用前需要进行剂量刻度标定，由于60Co γ射线被认为和空间辐射带的电子造成的影响类似［4，6］，RADFETs在使用前的标定通常都采用60Co γ射线源来进行。然而，根据AE9/AP9/SPM模型，空间的电离辐射源主要以质子（p）和电子（e）为主，内辐射带中质子占比相对外辐射带更高，太阳活动也会改变质子通量［7］，因此RADFETs在空间应用时，需要考虑质子的剂量响应以及质子辐照后对后续电子剂量响应的影响。目前的研究结果认为，RADFETs对不同质子、电子以及γ的电离辐射响应都能够保持较好的线性响应［5，8-9］，但这些研究结果都是在单一辐射源条件下实验得到的，并没有考虑空间实际存在的不同入射粒子的共同作用所产生的协和问题。

因此，针对RADFETs在地面标定使用60Co γ源而实际空间应用时的质子与电子辐射环境的差异性，以及质子和60Co γ复合场环境下的响应机制问题，本文分别进行了单独γ辐照实验和先质子后γ的协和辐照实验，并通过中带电压法和电荷泵法分离氧化物陷阱电荷和界面态陷阱电荷的影响，结合Geant4仿真PKA（Primary Knock-on Atom）的产生，对响应的微观物理机制进行了解释，为RADFETs的空间环境应用提供了参考。

1 实验器件与过程

实验器件为Tyndall公司400 nm栅氧厚度的RADFETs，结构如图1所示［10］。辐照灵敏区为栅氧介质，下端的支撑衬垫作为射线的背散射模体，与普通MOSFETs结构相比，RADFETs具有更厚的氧化层以及更大的有源区面积，因此剂量响应更加灵敏。辐照器件根据栅压条件分为两组：一组辐照时所有管脚短接，即栅端为0 V，另一组器件栅端接4 V电压，其余管脚接地。

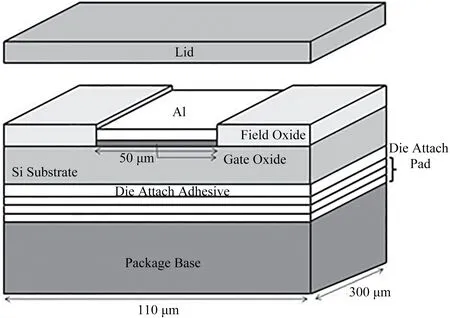
图1 RADFET器件结构示意图Fig.1 Schematic diagram of the RADFET device structure

辐照总剂量为40 krad（SiO2），辐照次序为先质子后γ辐照，质子剂量分别为0 krad（SiO2）、10 krad（SiO2）和20 krad（SiO2）。质子剂量D通过线性能量转移系数（Linear Energy Transfer，LET）换算：

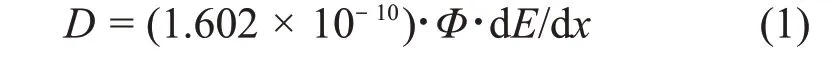
式中：Φ为质子注量，对应注量点分别为0、1.7×1010p·cm-2和3.4×1010p·cm-2；dE/dx为10 MeV质子在SiO2中的LET值。γ辐照在中国科学院新疆理化技术研究所的60Co γ辐照装置上进行，剂量场在辐照前通过PTW-UNIDOSE剂量计进行了标定，换算为等效SiO2吸收剂量，剂量率为18.7 rad·s-1（SiO2）。

2 结果分析与讨论

2.1 阈值电压漂移（ΔVth）

在每个剂量点，我们测试了器件的转移特性曲线，通过最大跨导法提取出了器件的阈值电压。辐照栅压为0 V的ΔVth随累积剂量的变化如图2（a）所示，栅压为4 V的结果如图2（b）所示。

从图2可以看到，在10 krad（SiO2）和20 krad（SiO2）等效剂量点下，栅压0 V时10 MeV质子辐照导致的ΔVth仅为γ辐照情况的30%左右，原因一是剂量换算没有考虑氧化层上部其他材料层的屏蔽以及薄材料层剂量的误差，二是质子和γ辐照电荷产额的差异导致的。栅压为4 V时，ΔVth的变化量是0 V情况下的5～6倍，质子导致的ΔVth与γ结果差异更大，即栅压增加对质子电离过程的影响相对较小。

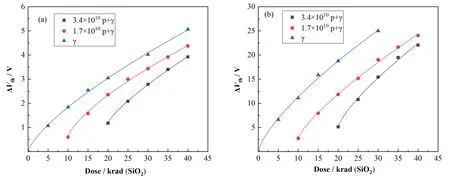
图2 RADFETs随累积剂量的阈值电压漂移量及拟合曲线(a)栅压为0 V，(b)栅压为4 VFig.2 Change of theΔVth change with accumulated dose and the fitted curve(a)Gate voltage at 0 V,(b)Gate voltage at 4 V

RADFETs作为剂量计的基础，是其阈值电压随着累积剂量的变化呈一定关系，在此选用Kimoto and Jaksic响应模型［4］，可表示为式（2）：

式中：ΔVth为器件的阈值电压漂移量；D为器件的累积吸收剂量；A和n表示电场、氧化层厚度、剂量等因素的线性依赖度。在理想情况下，n=1，响应呈线性关系。通过式（2）的拟合，得到不同实验组的拟合参数（表1），拟合曲线如图2所示。4 V栅压的结果与0 V结果相比，线性度参数n差异并不大，而灵敏度参数A升高5～8倍。10 MeV质子辐照后再进行γ辐照，RADFETs对γ射线的剂量响应依然可以与Kimoto and Jaksic响应模型较好的拟合，而且线性度n比单独γ辐照的结果更高，残差平方和（Residual Sum of Squares，RSS）更小。

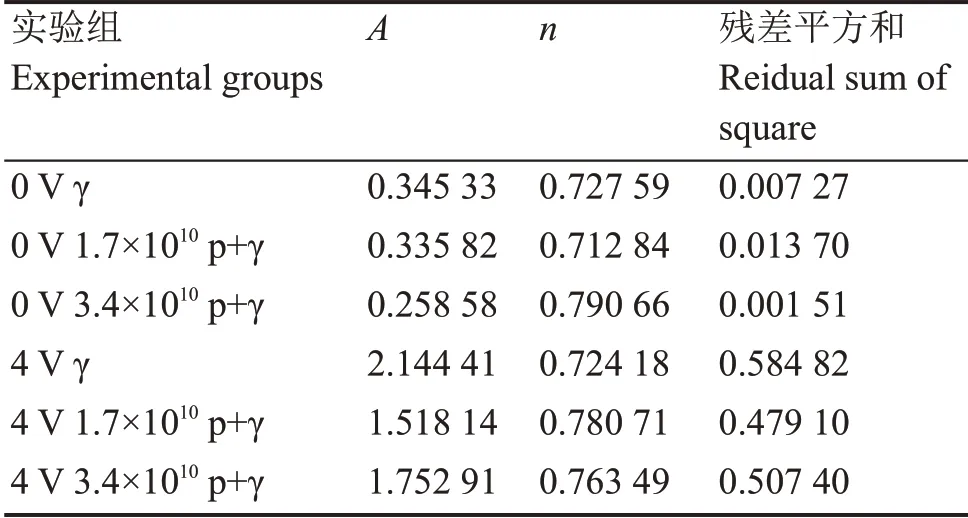
表1 Kimoto and Jaksic响应模型拟合参数Table 1 The fitting parameters of Kimoto and Jaksic model

质子在SiO2中阻止本领较大，产生的电子-空穴对较γ更为密集，更加符合柱状复合模型，复合率更高。因此逃出初始复合的空穴（即电荷产额）低，最后形成的陷阱电荷数目更少［6］，因此质子的剂量响应相对γ较差。栅压为4 V的情况下，栅氧介质中的电场会使得电子空穴对的1/r势垒边界发生畸变（Frenkel-Poole效应），电子更容易逃离出势垒范围，使得电子-空穴对的复合变少，最终的电荷产额增加（图3），从而RADFETs的灵敏度提高［11］。在Srour等的研究中［12］，说明了电场对位移损伤的影响可以忽略，电场主要是通过改变电离辐射后的复合机制来改变对器件参数的影响。

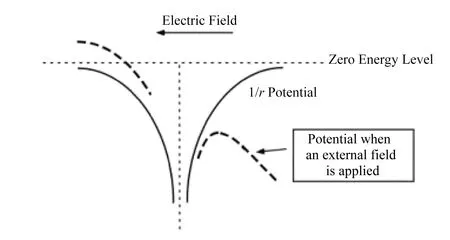
图3 外加电场作用下势垒边界的畸变Fig.3 Distortion of the potential well when an external electric field is applied

为了分析辐照过程中的微观机制，中带电压法（Mid-gap Technique，MGT）和 电 荷 泵法（Charge Pump，CP）被用来分离氧化物陷阱电荷密度（ΔNot）和界面态陷阱电荷密度（ΔNit）的变化。

2.2 氧化物陷阱电荷和界面态陷阱电荷分离

中带电压法是利用界面态陷阱电荷在价带中心呈电中性的原理［13］，以中带电压的变化量为氧化物陷阱导致的阈值电压变化量，由式（3）、（4）决定ΔNit和ΔNot：

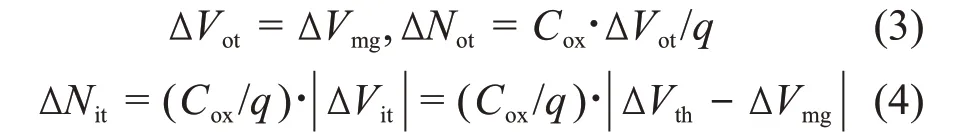
式中：ΔVmg表示中带电压的变化量；Cox表示栅氧介质的电容；q表示单位电荷。

MGT法分离的ΔNot和ΔNit分别如图4（a）和（b）所示。

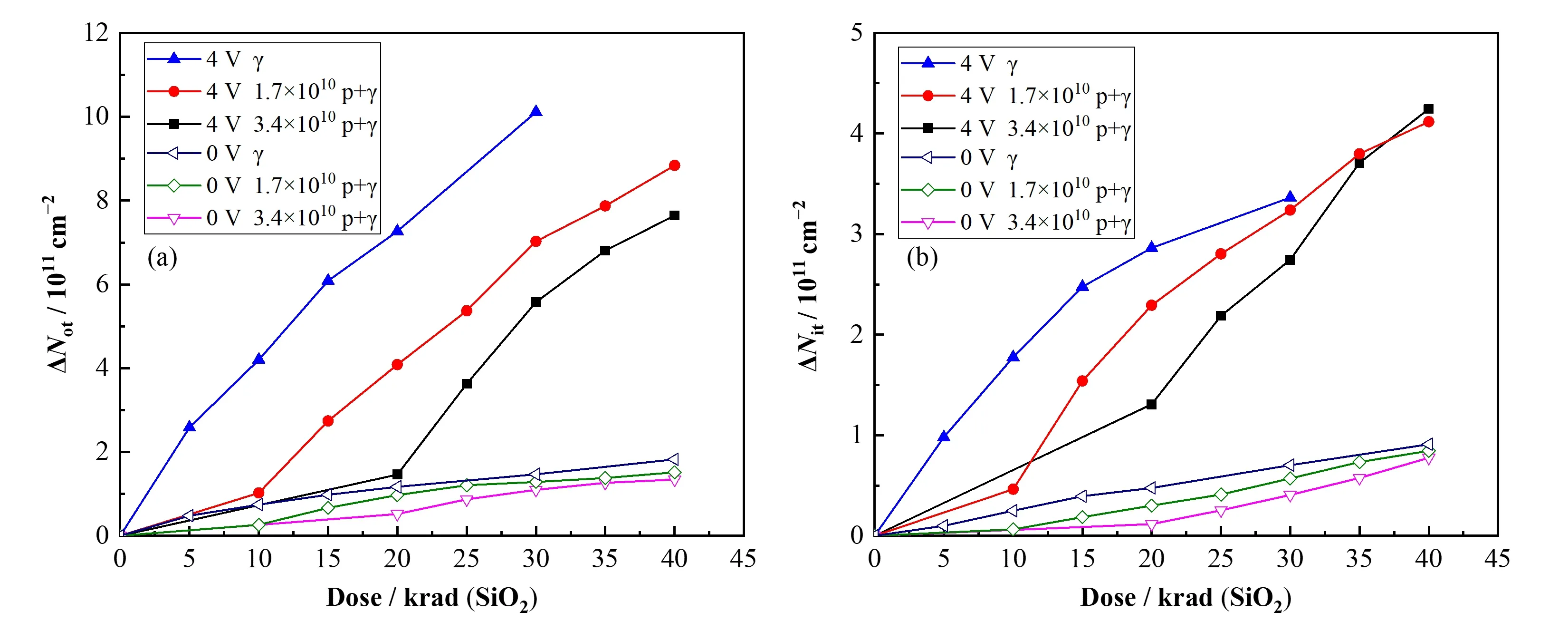
图4 MGT分离陷阱电荷密度随累积剂量的变化(a)ΔNot，(b)ΔNitFig.4 Change of the charge density with the accumulated dose separated by MGT(a)ΔNot,(b)ΔNit

ΔNot的变化通常由E'陷阱中心模型和极子假设中的空穴捕获活动来解释［15］。从分离结果可以看到，质子辐照导致的ΔNot明显小于γ辐照后，原因是质子辐照逃出初始复合的空穴数目更少［6］。在质子辐照后进行γ辐照的ΔNot在栅压为0 V时差异并不大，栅压为4 V时明显观察到ΔNot的显著增加，考虑0 V栅压的电荷产额并不高，空穴捕获概率保持不变，所以差异不大，但存在电场后，电荷产额明显增加，使得陷阱捕获的空穴数显著增加。

对于ΔNit的变化，目前的研究主要通过氢输运模型解释［15-17］。在电子-空穴对产生复合以及输运过程中，栅氧介质中会释放一部分的氢，氢通过势阱间的跳跃向SiO2/Si界面输运。在邻近界面时，由于存在一个较大的势垒，质子会横向输运，在横向输运过程中可能被捕获形成陷阱电荷。在栅压为0 V时，ΔNit的变化不明显，而栅压为4 V时存在较大差异。质子辐照后再进行γ射线辐照时ΔNit的变化增强，可能是质子引入了新的界面陷阱导致的，考虑到中带电压法存在一定误差，电荷泵法被用于ΔNit的分离来进行对比。

电荷泵法是在栅极加一个扫描电压脉冲，使沟道在积累和反型状态间不断转换，从而使漏源区的少数载流子在SiO2/Si界面陷阱上与衬底的多数载流子反复复合，由此产生净的衬底电流，即电荷泵电流（Icp）。通过分析扫描脉冲与电荷泵电流的关系，得到界面陷阱电荷的信息［14］，Nit(cm-2)由式（5）决定：

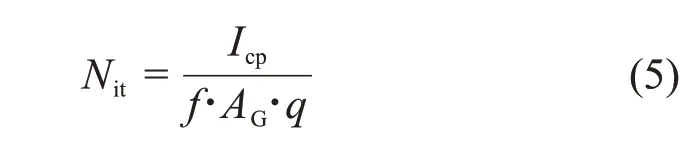
式中：Icp表示电荷泵电流；f为扫描频率（采用1 MHz）；AG为有效沟道面积；q为单位电荷。

分离结果如图5所示。从电荷泵法分离的ΔNit变化趋势可以看出，在相同的入射粒子辐照下，界面态变化随累积剂量的变化呈较好的线性关系，质子辐照导致的界面态依旧小于γ辐照。存在栅压下的ΔNit反而小于没有栅压的情况。质子辐照后再进行γ辐照与全部γ辐照时的变化趋势一致，没有MGT分离的ΔNit变化增强现象。

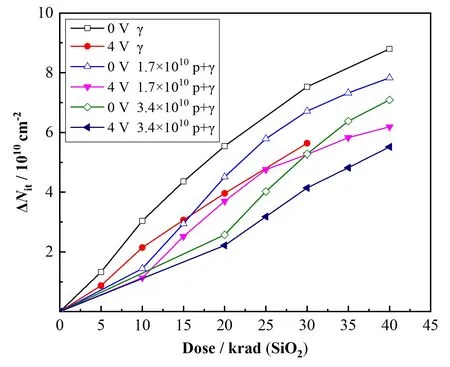
图5 电荷泵法分离ΔNit随累积剂量的变化Fig.5 Change of theΔNit change with the accumulated dose separated by CP

电荷泵法分离结果与中带电压法的结果存在一定 差 异，Ristic等［18-19］使 用 快 转 换 态 陷 阱（Fast Switch Trap，FST）和慢转换态陷阱（Slow Switch Tarp，SST）进行了解释。CP法分离的界面态只包含FST，即真界面态陷阱电荷，而MGT法分离的界面态包含了FST和SST。MGT将一部分邻近界面处的陷阱电荷（SST）也分离为界面陷阱电荷，这是CP分离的ΔNit明显小于MGT分离结果的原因。因此两种方法差异的来源在于SST的影响。通过两种方法的结果对比，可以认为质子使得邻近界面处的陷阱捕获空穴活动增强，或者质子在邻近界面处引入了新的陷阱。为了讨论质子引入的陷阱情况，Geant4工具包被用来仿真质子在SiO2中的初级反冲原子（Primary Knock-on Atom，PKA）产生过程。

2.3 Geant4仿真质子在SiO2中的初级反冲原子产生

质子除了电离效应之外，还会在材料晶体中形成点缺陷或团簇缺陷，这些辐射诱发的缺陷可能是电中性或电活性的，电活性的缺陷可以成为载流子的产生-复合中心或者捕获中心，最终会导致器件的电参数变化。为了从微观层面探索界面态陷阱电荷产生差异的来源，Geant4（Geometry and Tracking）工具包被用来仿真质子入射后与栅氧介质的相互作用过程，Geant4是由欧洲核子中心开发的开源蒙特卡罗计算工具，在射线与物质相互作用的仿真计算上有很好的适用性与灵活性［20］。

通过SRIM软件计算得到10 MeV质子在SiO2中的射程为709 μm，在Geant4中建立了2 cm×2 cm×709 μm的SiO2靶几何模型，记录质子在栅介质SiO2中的PKA相关信息。注册的物理过程包括电磁物理过程G4hIonisation，质子弹性散射G4 HadronElastic，非弹性散射G4CascadeInterface，与核相关的物理过程G4IonElasticPhysics、G4 BinaryLightIonReaction，与γ相 关 的 物 理 过 程GammaNuclearPhysics，仿真粒子数为2×109。

沿入射深度的PKA数目如图6所示，在SiO2中产生的PKA信息如表2所示，可以看到，入射深度较浅时，PKA数目较稳定，随入射深度增加，PKA数目缓慢上升，在射程尾部形成一个布拉格峰后迅速下降，这是由于随着质子能量降低，散射截面的增加导致的。对于400 nm栅氧厚度的RADFETs，PKA在栅介质中呈相对均匀的分布。

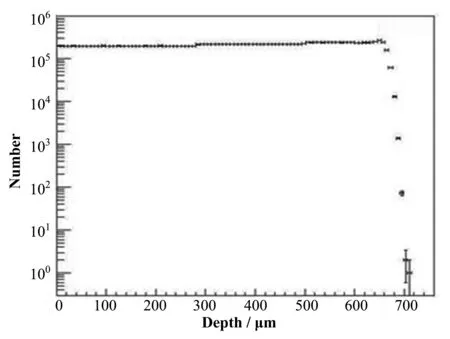
图6 10 MeV质子在SiO2中产生的PKA沿深度位置信息图Fig.6 Change of the 10 MeV proton-induced PKA number with the depth in SiO2

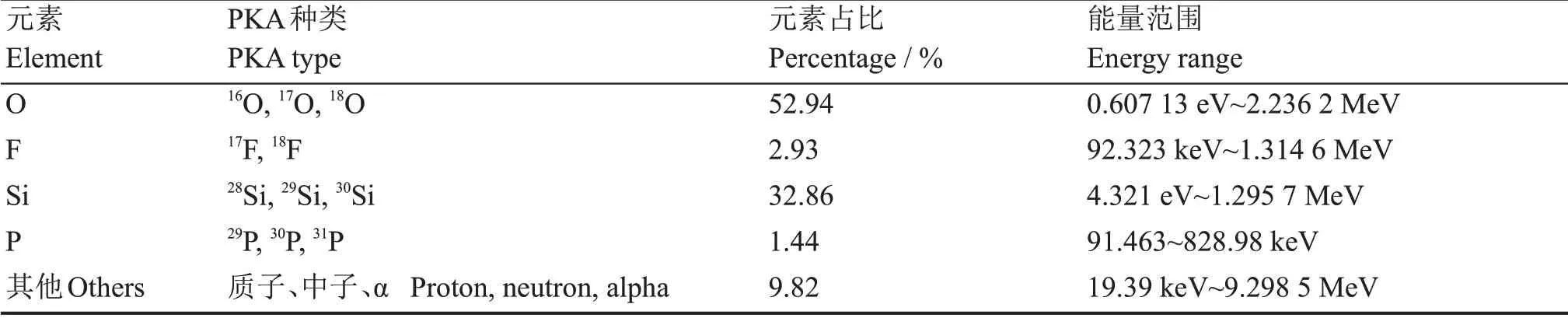
表2 10 MeV质子入射SiO2模拟的PKA信息Table 2 PKA information generated by 10 MeV proton in SiO2

从仿真结果可以看到，质子在氧化层中引入了一定量的初级反冲原子，PKA相对均匀分布在氧化层中，最终PKA演化形成的位移缺陷会由PKA的种类、能量以及氧化层材料特性等因素决定。由于产生的反应截面很小，对器件而言，氧化层内部位移缺陷的作用并不明显，而边界处的陷阱捕获电荷活动的影响较大，边界处陷阱电荷对沟道载流子的影响也更大。

对于RADFETs而言，主要考虑其阈值电压漂移量与累积剂量的关系。这部分影响是由栅氧化层中的辐射诱发陷阱电荷决定的。在工艺条件确定的情况下，栅氧介质中的陷阱数目一定。随着累积剂量的增加，参与捕获的陷阱数目越来越少，则RADEFTs的线性度会逐渐降低。但是我们发现经过质子辐照后再进行γ辐照，拟合得到的线性度参数并无减少，反而有增加的现象，同时分离得到的陷阱电荷也表现出增加的趋势。我们认为是质子辐照引入的新的陷阱，使得捕获过程并未减弱。仿真显示PKA分布较为均匀，而陷阱电荷的分离说明临近界面处的电荷影响更大，这是由于邻近界面处捕获的电荷对沟道的影响更大。

从实验和仿真分析可以看到，RADFETs在空间混合场中的剂量响应与地面标定剂量存在一定误差，RADFETs对10 MeV质子的剂量响应较差，且质子引入的缺陷会使得后续剂量响应发生变化，这部分误差在进行相对剂量标定时可通过质子/电子通量模型进行修正或设计特定的剂量标定方案。

3 结语

针对RADFETs在地面标定使用60Co γ源而实际空间应用时的质子与电子辐射环境的差异性以及空间质子和γ复合场环境下的响应机制问题，本文通过质子和60Co γ的单独及协和辐照实验，探讨了RADFETs对质子、特别是质子与60Co γ协和辐照的响应特性及机制。实验表明：在栅压为0 V和4 V的情况下，质子导致的ΔVth都小于γ辐照，质子辐照后RADFETs对γ响应的线性度略微增加。通过中带电压法和电荷泵法对陷阱电荷进行分离，发现质子辐照对邻近界面的陷阱电荷影响较大，且存在栅压时影响更大。Geant4仿真显示，质子在RADFET的栅氧中均匀产生了PKA。因此，使用60Co标定的RADFETs在测量空间环境剂量时，需要考虑剂量的射线成分差异。研究认为，RADFETs对于质子的电离效应响应较差，但质子会引入一定的位移损伤，加剧邻近界面处的陷阱电荷的影响。空间应用时可使用质子电子的通量模型对数据进行修正或设计特定的剂量标定方案。

作者贡献声明马函负责文章的起草及最终版本修订；孙静负责实验器件及实验流程的相关内容；何承发负责研究的提出与设计；荀明珠提供了仿真方面的帮助。