RPV下封头熔融池换热特性数值模拟研究

朱光昱闵金坤靖剑平王昆鹏刘福东

1（生态环境部核与辐射安全中心北京100082）

2（国家环境保护核与辐射安全审评模拟分析与验证重点实验室北京102488）

3（中国核电工程有限公司北京100840）

4（清华大学工程物理系北京100084）

核电厂发生严重事故后，堆芯各类构件由于失去冷却后熔化，逐渐在压力容器下封头内形成了Fe、Zr和UO2-ZrO2组成的高温熔融池。为防止事故进一步发展造成大规模放射性释放后果，第三代核电厂设计过程中均进行了堆芯熔融物滞留设计。主要包括：将熔融物滞留在压力容器内的堆内滞留（In-vessel Retention，IVR）技术［1］，以及在压力容器破损后将熔融物重新收集冷却的堆外滞留（Exvessel Retention，EVR）技术［2］。我国的先进压水堆设计更倾向于采用IVR技术，在第三代反应堆（如HPR1000）以及随后的新型设计中均使用了该策略［3］。

在堆芯熔融池形成后，由于轻金属与氧化物并不相溶，金属层会浮于氧化物层之上形成双层熔融池结构［4］。在此基础上，由于部分析出的U与Zr混合可能会形成重金属层，而形成三层熔融池结构。然而，根据Bechta等［5］基于熔融池中U-Zr-Fe-O的相平衡机理分析结果，三层熔融池仅属于过渡段形态，双层结构是熔融池发展的最终形态。由于轻金属层的热聚集效应会使反应堆压力容器（Reactor Pressure Vessel，RPV）下封头更容易发生熔穿，在IVR设计过程中必须考虑双层熔融池对压力容器完整性的挑战。由于真实熔融物的大尺度熔融池实验存在一定困难，国内外一些学者采用数值模拟手段对双层［6-7］或三层［8-9］熔融池的热工水力特性、金属层的聚焦效应和下封头机械性能进行了研究。本文基于当前大型三代压水堆的设计参数，采用COMSOL Multiphysics多物理场耦合软件建立了一个双层熔融池仿真模型，对RPV下封头内双层熔融池的换热特性进行了数值模拟研究。

1 仿真模型

1.1 计算域设置

图1为采用四边形网格建立的二维轴对称计算模型，其中熔融池半径为2.2 m，下封头厚度为0.15 m，下封头顶部区域延伸了长度为0.4 m的不锈钢壁面。仿真过程中，温度场采用固体、流体传热模型计算，流场采用低雷诺数k-ε模型［4，10］计算，通过非等温流动模块进行多物理场耦合。

图1 计算域和网格划分示意图Fig.1 Diagram of calculation domain and mesh generation

计算域中，氧化物层高度为1.58 m，金属层高度为0.56 m，金属层顶部和下封头延伸部分的内壁面均设置为表面对环境辐射条件，发射率分别设置为0.45和0.8［1］。目前，大型压水堆采用的堆腔注水冷却系统均是从下封头底部注入冷却水，所以沿着下封头弧形面由下至上的冷却水流速是逐渐降低，因此循环流速一般采用通道内平均流速表征。在AP1000堆型以及国内自主研发的国和一号堆型中，堆内熔融物滞留系统的冷却水循环流量分别为3 000 t·h-1和3 800 t·h-1，结合流道尺寸计算平均流速分别为0.5 m·s-1和0.6 m·s-1。结合上述参考，将下封头外侧设置为强制对流换热边界条件，冷却水侧流速取0.5 m·s-1，过冷度设置为50 K。

在熔融物稳定分层后，可以认为衰变热全部集中在氧化物层中，其内热源可采用式（1）计算：

式中：Q为堆芯衰变热功率，MW；fd为衰变热修正系数，可设置为0.75［11］；P0可认为是反应堆正常运行时的热功率，本文取3 050 MW；t为计算时长，s。

考虑到事故初期并未形成双层熔融池，仿真过程中，由事故发生4 h后开始进行计算，氧化物层的初始体积释热率约为1.49 MW·m-3。

1.2 物性设置

熔融池内通过引入相变模型模拟凝固过程，材料密度采用Boussinesq近似［4］处理。其中，氧化物层参考温度为2 650 K，参考密度为8 196.41 kg·m-3，完全凝固后的密度和导热系数设置为9 512.8 kg·m-3和2.8 W·m-1·K-1。金属层参考温度为1 750 K，参考密度为6 818.50 kg·m-3。根据VULCANO熔融物铺展实验相关数值模拟经验［12］，可以采用式（2）计算各层熔融池中糊状区的黏度。

式中：μl为液相黏度，氧化物层和金属层分别取0.008 12 Pa·s和0.003 01 Pa·s；系数C一般取3.5～8［13］；θs为固相体积分数，可直接在计算过程中实时调用参数。

熔融池内其他计算所需物性参照文献［4］和［14］设置，具体如表1所示。冷却水参数直接引用COMSOL数据库中的物性参数，不考虑实际工况下水中含有硼酸带来的影响。

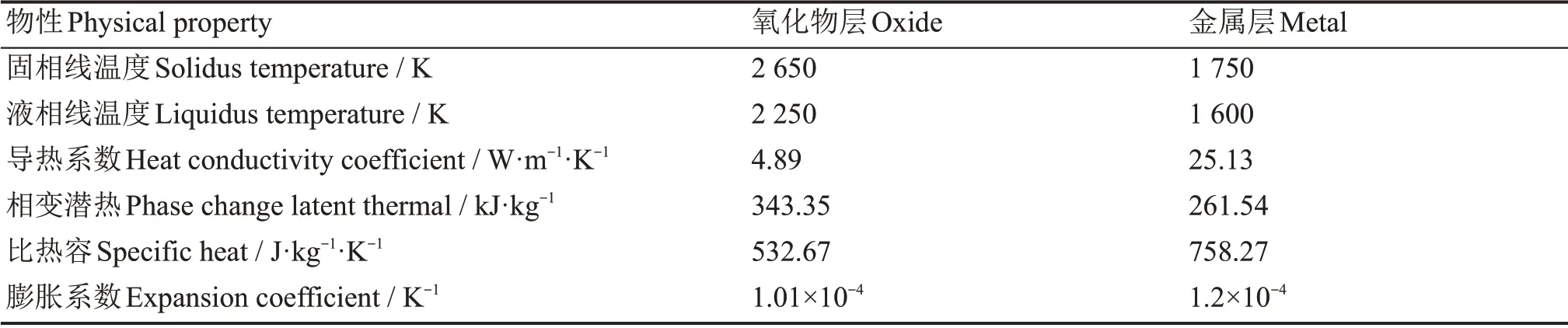
表1 物性参数Table 1 Physical property

计算过程中依然采用相变材料来模拟下封头熔化过程，熔化前下封头的材料物性设置为A508-3钢的物性，熔点为1 600 K，导热系数为32 W·m-1·K-1，相变潜热为269.55 kJ·kg-1，并设置了20 K的相变温度区间。由于实际计算中下封头与氧化物层接触区域没有发生熔化，与金属层接触区域熔化后的钢相对于金属层总质量而言很小，可以认为下封头熔化后的材料物性参数与金属层一致。在当前COMSOL计算模型中，下封头部分设置为固体域，无法模拟材料熔化后混入临近熔融池的过程，为了考虑下封头熔化区域内流动导致的换热，在材料本身的导热系数之外将湍流导热添加至熔化后区域的导热系数当中，湍流导热可采用式（3）计算。

式中：kT为湍流流动产生的导热系数，W·m-1·K-1；μ为湍流动力黏度，Pa·s，可在用户定义项中调用邻近金属层内的参数作为参考。PrT为湍流普朗特数，对于一般的湍流边界层问题取0.9。Cp为比热容，参照熔化后的金属层参数设置。

初始化过程中，氧化物层、金属层以及下封头的初始化温度分别设置为2 650 K、1 750 K和1 000 K。

1.3 网格无关性分析

经预计算测试，网格宽度大于1.7 cm后计算会直接发散，而网格数小于1.5 cm时，仅当计算时长较短时可以获得收敛结果。因此仅在网格宽度1.5～1.7 cm内进行网格无关性测试。图2为不同网格数下计算时长为0.5 h时，模型中轴线上的温度分布情况。网格数对氧化物层的温度分布影响很小，但对金属层温度分布影响较大。随着网格加密，金属层处的温度差异逐渐减小，本文最终采用的网格数为19 603的模型进行后续的仿真工作。

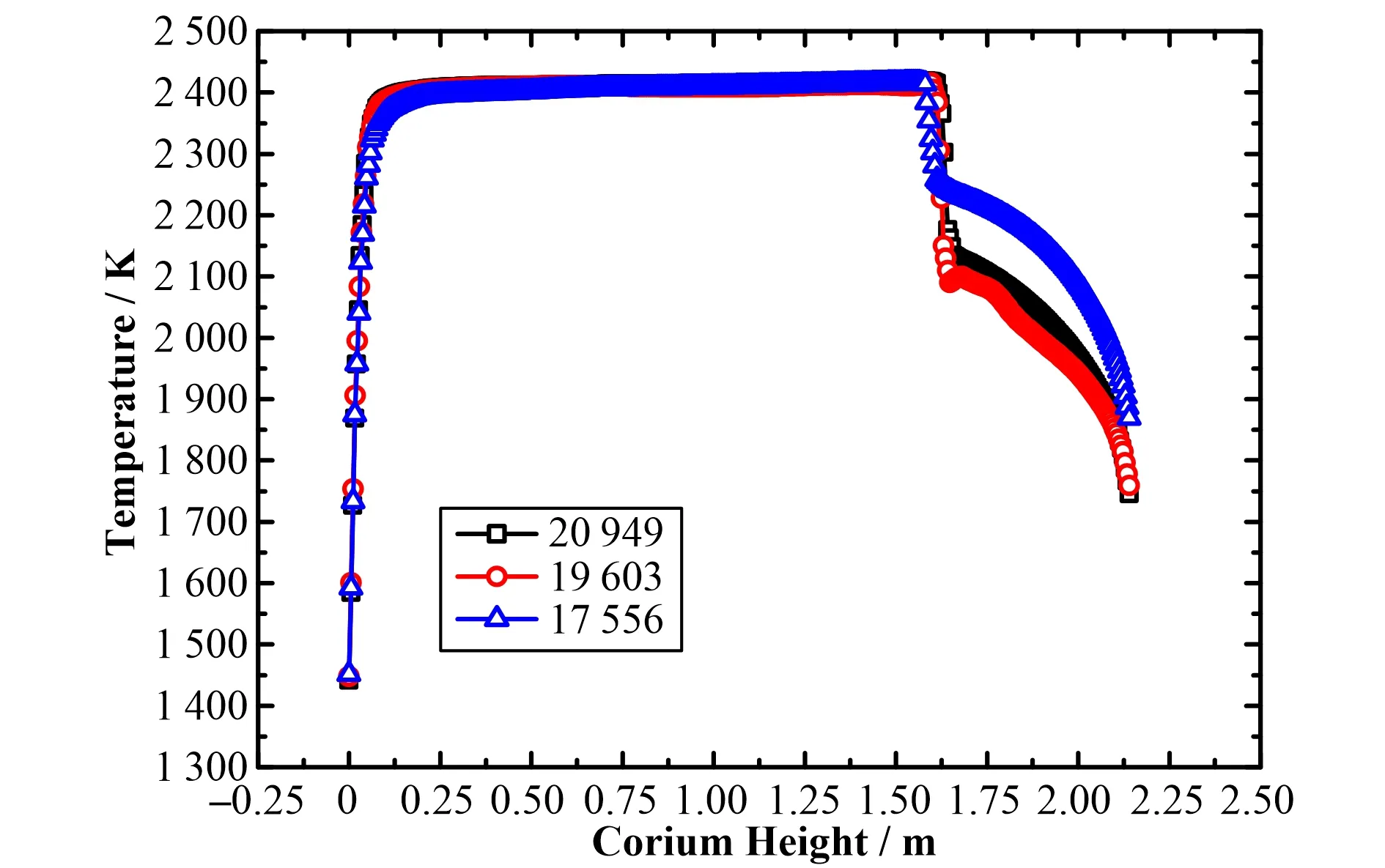
图2 不同网格数下的模型中轴温度分布Fig.2 Temperature distribution on the axis of calculation domain under different mesh number

2 计算结果分析

图3给出了计算时长为1 h、1.5 h和3 h的熔融池速度场。两层流体由于密度差异较大形成了稳定的分层状态，氧化物层在衰变热的作用下很快形成了自然循环，熔融物在靠近冷却壁面一侧受到冷却向下流动，在主流中受热后转向上流动。初始阶段金属层不存在稳定的循环流动状态，在约1.5 h时逐渐建立了自冷却壁面一侧向下、在吸收金属层热量后向上的自然循环流动。然而，与氧化物层始终存在一个稳定的自然循环流动不同，在顶部辐射换热冷却和底部氧化层流动剪切作用的共同影响下，除了冷却壁面附近存在一个较稳定的自然循环外，金属层中还同时存在多个不断变动的涡流，导致流场不断发生变动。

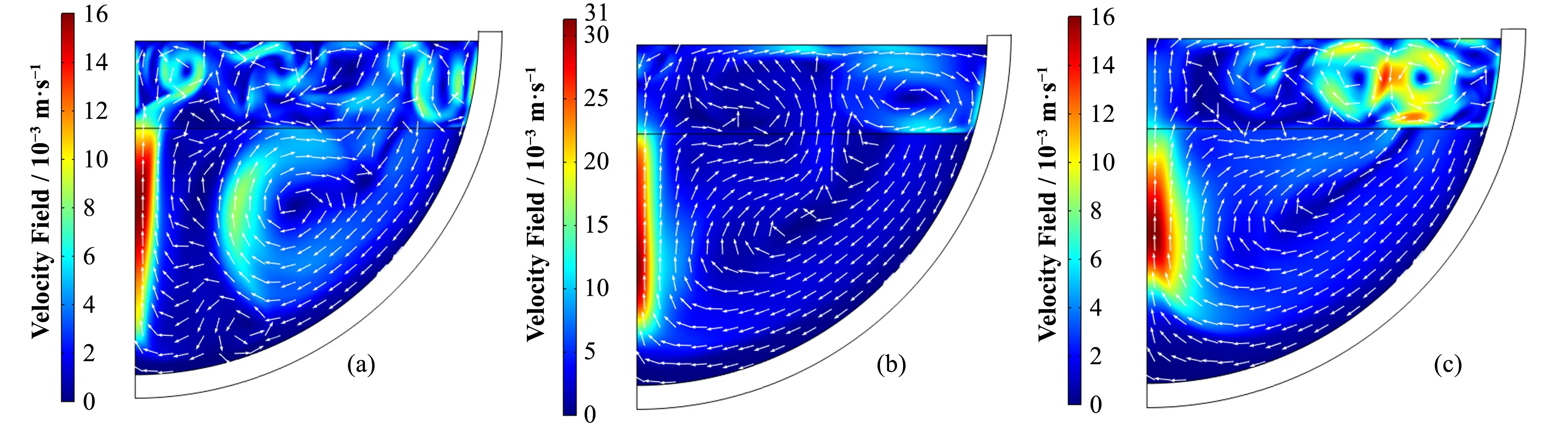
图3熔融池内的速度场(a)1 h，(b)1.5 h，(c)3 hFig.3 Velocity field of RPV corium pool(a)1 h,(b)1.5 h,(c)3 h

图4 展示了当计算时长为2 h时，下封头和熔融池内的温度场。在自然循环流动的搅拌作用下，氧化物层和金属层的温度近似一致且分布较为均匀，没有出现明显的热分层现象。在金属层热聚集效应作用下，与其接触的下封头温度明显升高，而与氧化物层接触的下封头温度则相对较低。

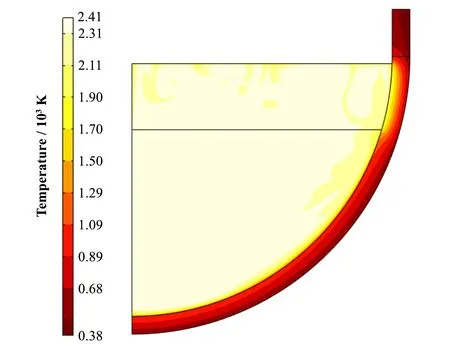
图4下封头和熔融池温度分布Fig.4 Temperature distribution of RPV lower head and corium pool

图5 展示了当计算时长为1 h时，各计算域内的固相体积分数，此时氧化物层已经进入到UO2-ZrO2糊状区状态而金属层则依然保持纯液态状态。此外，氧化物层中的熔融物会迅速在下封头处结壳，在低导热系数硬壳的良好保护和外侧冷却水的共同作用下，该区域的下封头并未发生明显的熔化。与金属层中接触的下封头区域由于温度超过熔点发生了明显的熔化，但最薄的区域的厚度依然大于10 cm。

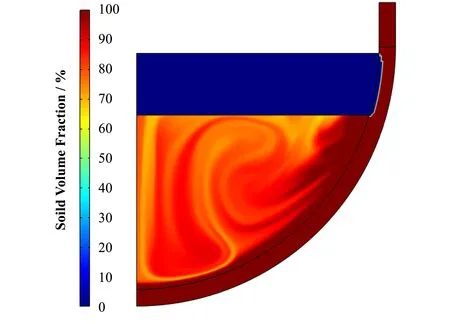
图5 下封头和熔融池内固相体积分数Fig.5 Soild volume fraction of RPV lower head and corium pool

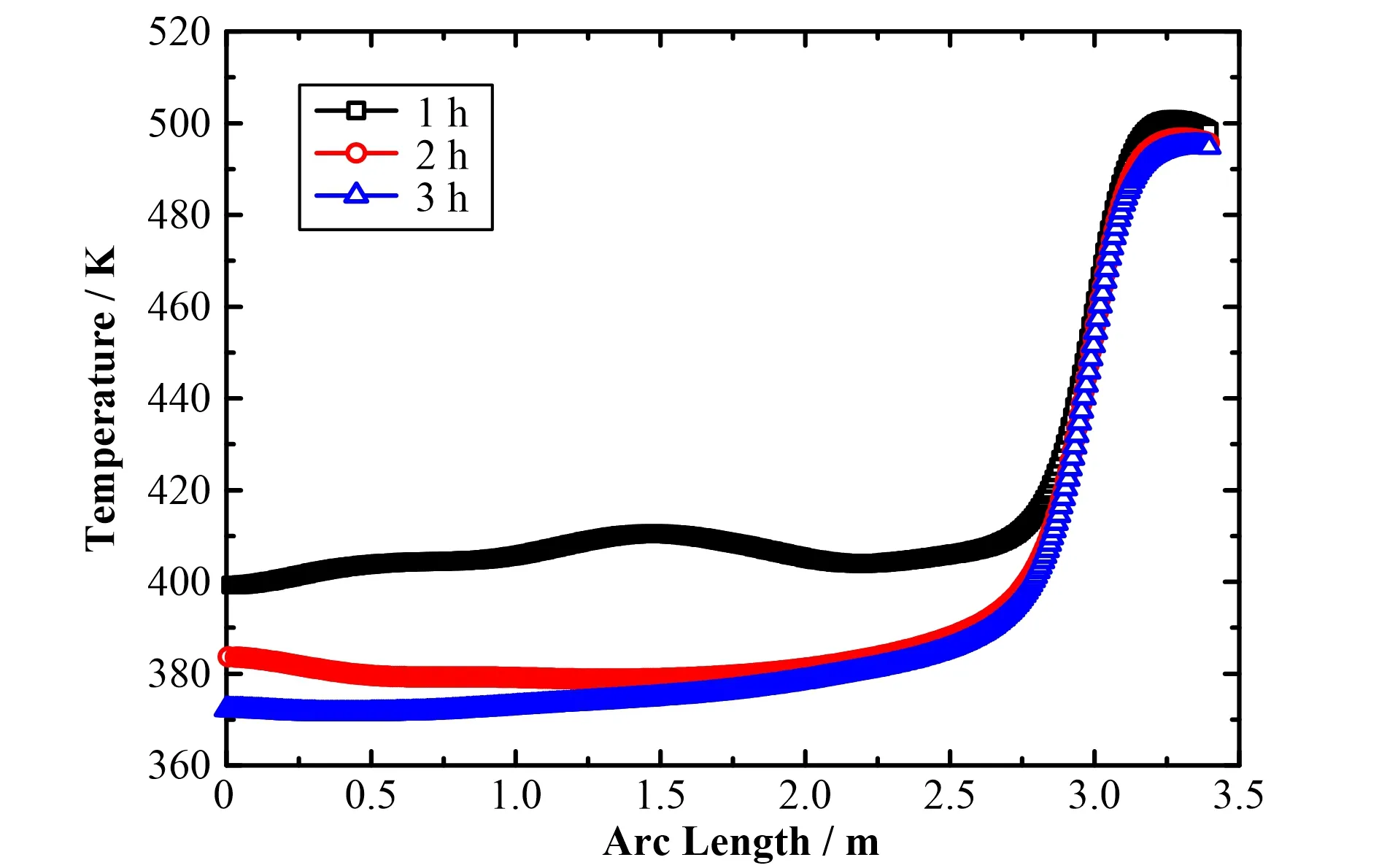
图6下封头外壁面温度分布Fig.6 Temperature distribution on outer wall of RPV lower head

图6为下封头计算时间1～3 h时下封头外壁面的温度分布，可见对于双层熔融池结构，将下封头外壁面考虑为强制对流冷却边界条件时下封头外壁面温度分布并不均匀，与金属层接触的下封头区域温度会显著升高。图7为计算时间1 h时下封头计算域内的热流密度分布，金属层导入的热量除了向冷却水侧径向传递之外，还会沿着下封头不锈钢壁面进行周向传递。对比张卢腾等［4］将冷却壁面设置为400 K恒温壁面得到的仿真结果，在径向角度50°以下的区域，外壁面处的热流密度均在0.15～0.20 MW·m-1。然而，在与金属层接触的区域，当前模型计算得到的热流密度显著低于张卢腾［4］的计算结果。

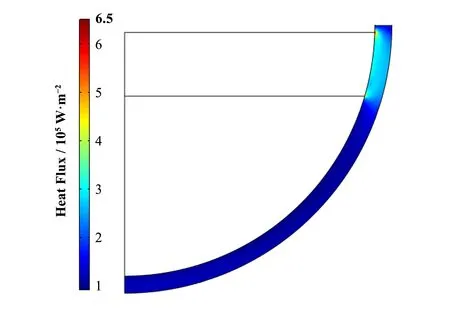
图7 下封头计算域内热流密度分布Fig.7 Distribution of heat flux in RPV lower head calculation domain

根据图6所示温度分布，与金属层接触的下封头外侧应处于沸腾状态，因此采用强制对流边界条件计算得到的换热量会偏低。综合上述分析，对于下封头外部的冷却壁面而言，采用单一的恒温壁面模型或强制对流换热模型进行仿真仍具有很大的局限性，相关仿真模型尚有改进空间。

3 结语

采用COMSOL软件建立了一个熔融池仿真模型，对核电厂严重事故后压力容器下封头内双层熔融池的演变进行了仿真研究，结论如下：

1）在稳定分层情况下，氧化物层会迅速形成存在稳定的自然循环。金属层中除靠近冷却壁面的区域存在稳定自然循环外，在其他区域还存在一些不稳定的涡流。

2）在自然循环和涡流的搅浑作用下，氧化物层和金属温度分布较为均匀，不会发生热分层现象。

3）氧化物层中，熔融物会迅速在冷却壁面附近结壳，从而防止该区域下封头熔化。由于金属层的热聚集效应，与其接触的下封头会发生明显的熔化，但在良好的冷却条件下，不会发生熔穿现象。

作者贡献声明朱光昱：采集数据和文章撰写；闵金坤、靖剑平、王昆鹏：文章撰写；刘福东：工作支持。