水陆两栖式水生植物收割装置运动分析与仿真

王 斐，周竹馨，沈 辉

（1.江苏联合职业技术学院 扬州分院，江苏 扬州 225003；2.扬州大学 机械工程学院，江苏 扬州 225127）

湿地水生植物收割作业量大，采用传统人工方式劳动强度大、工作效率低。水陆两栖式水生植物收割装置可适应复杂湿地环境下的行走和对挺水植物的切割，作业效率高，成本低，可满足市场需求[1]，而切割器作为工作装置的关键部件，其性能将直接影响切割质量及收割效率。本文对水陆两栖式水生植物收割装置切割器进行运动学分析与仿真，以期为后期生产提供理论依据。

1 总体结构与工作原理

水陆两栖式水生植物收割装置的结构如图1 所示,该装置由车架、行走底盘、动力单元、连接架、提升架、快换接头和工作装置等组成。提升架的作用是调整工作装置的高度，控制切割高度；连接架起到伸长和减震的作用；快换接头方便工作装置的安装和拆卸，可装配不同的工作装置，满足多功能的需求。工作机除装配T 型刀头用来收割水草和湿地植被外，也可装配钻头用于厚冰钻孔，进行冰上抢险救灾。

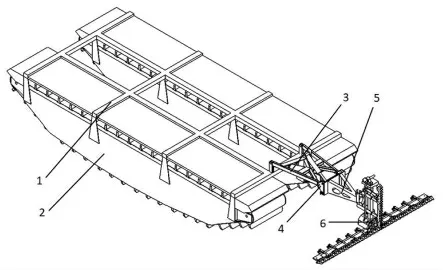
图1 湿地轻型两栖式多功能工作机结构

2 往复式切割器工作原理与运动分析

2.1 工作原理

往复式切割器结构如图2 所示，工作原理如图3 所示。

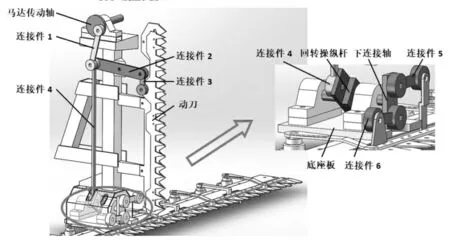
图2 往复式切割器结构

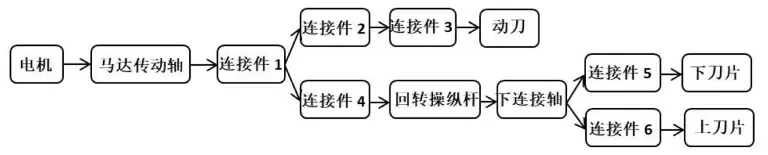
图3 工作原理

2.2 割刀运动方程

割刀的运动特性将对切割器性能产生直接影响，为此，可以将往复式切割器简化为曲柄连杆机构，连杆在曲柄的驱动下做往复直线运动，如图4 所示。

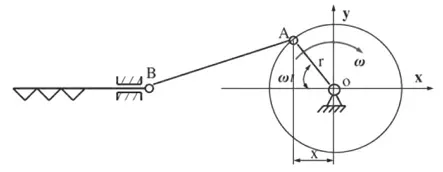
图4 切割器的机构运动简图

建立动刀片的运动方程[2]：

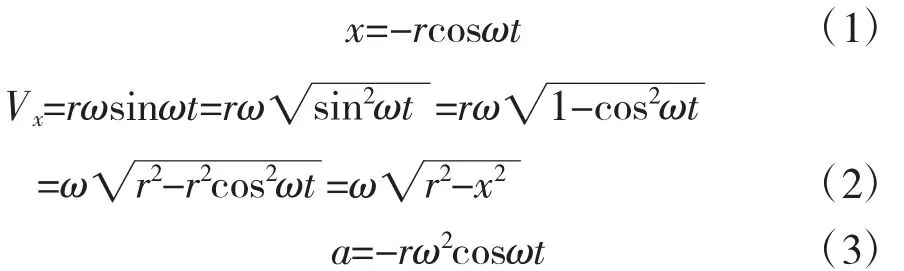
其中：ω 为动刀片的角速度，rad/s；r 为曲柄半径，mm；x 为割刀位移，mm；Vx为割刀在x 方向的速度，mm/s；t 为时间，s；a 为加速度，mm/s2。

联立式（1）、式（2）可得式（4）：

可以看出，割刀速度与割刀位移的关系满足椭圆方程式，椭圆长半轴的长度为rω，短半轴的长度为r，如图5 所示，说明割刀上任一点的速度都不相同。

图5 割刀速度与割刀位移的关系

综上可知，刀片上某一点的速度变化规律与椭圆方程式是一致的。当位移为零，即x =0 时，该点位于刀片的中点，此时Vx取得最大值，即为rω；当位移为r，即x=±r 时，该点位于刀片的极左或极右处，此时Vx=0，为最小值。

2.3 工作机运动学仿真

为直观地分析切割器工作过程中刀具的位移、速度和加速度特性，使用ADAMS 软件进行运动学仿真分析[3]。利用电动机带动传动轴转动，转速为550 r/min。由图6 可以看出，割刀的位移曲线为正弦曲线，曲线的波峰和波谷值是动刀片在两个不同方向上的最大位移。

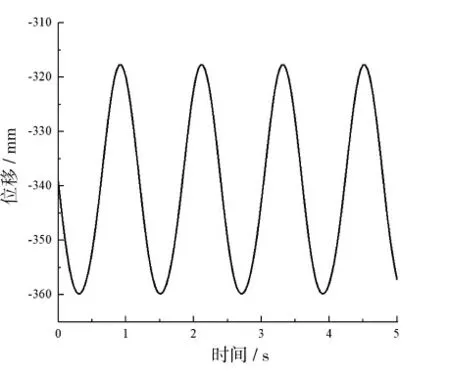
图6 割刀位移随时间变化曲线

由图7 可以看出，当曲柄以恒定速度旋转时，在连杆的驱动下，割刀的速度变化曲线可以近似为正弦变化。动刀片的最大速度值出现在初始点，动刀片的零速度在其最大位移处。

图7 割刀速度随时间变化曲线

由图8 可以看出，割刀的加速度变化曲线也呈近似正弦曲线。割刀的最大加速度出现在其最大位移处，而最小加速度出现在初始点。

图8 割刀加速度随时间变化曲线

3 性能试验研究

在挺水植物及沉水植物生长茂盛期间，对湿地轻型两栖式多功能工作机综合切割性能进行测试，测试结果见表1 所示。表1 结果表明：该湿地轻型两栖式多功能工作机可以通过调节切割深度在复杂地形条件下连续切割沉水植物和大面积挺水植物，在一定条件下满足复杂的两栖作业要求，工作性能稳定可靠，达到动力与效率的平衡。

表1 两栖式多功能工作机切割性能试验结果

4 结 论

（1）对湿地轻型两栖式多功能工作机的关键部件进行了运动分析，从理论上证明割刀相对于时间的位移、速度、加速度变化曲线均呈正弦规律。

（2）在软件ADAMS 中进行运动学仿真分析，得到割刀位移、速度和加速度的变化曲线，割刀的最大速度出现在初始点，零速度出现在割刀的最大位移处；割刀的最大加速度出现在其最大位移处，最小加速度出现在初始点。

（3）试验结果表明，湿地轻型两栖式多功能工作机在满足设计要求的同时也能保证工作效率。

对于湿地轻型两栖式多功能工作机的传动系统以及切割器刀片的高度确定还需要进一步研究，以达到更好的切割效果。