非规则坡面形态对高位滑体失稳的影响研究

胡昌文，赵腾，龚小根

（1.深圳市综合交通设计研究院有限公司，广东 深圳 518003；2.中南大学 土木工程学院，湖南 长沙 410075）

滑坡与静态边坡的稳定性分析不同，是一个变形、解体、运动、堆积的动态过程[1-5]。在中国，滑坡地质灾害日渐增多，造成了严重的人员伤亡和惨重的经济损失。因此，研究滑体失稳，提高边坡稳定性，至关重要[6]。针对滑坡失稳过程中的运动特性，国内外进行了很多研究。崔涛[7]针对壶大某公路段改扩建工程边坡滑坡灾害，通过现场工程地质调查与勘探，分析边坡滑坡失稳机制，提出了加固方案，并采用数值分析方法进行验证。鲁志雄等人[8]运用地貌学和工程地质力学等方法对滑坡变形失稳影响因素进行分析，并提出应合理规划以减少灾害的发生。王升等人[9]采用更新拉格朗日控制方程的物质点法，建立了滑坡二维模型，模拟滑坡失稳、运动和冲击过程，其结果表明：物质点法模拟分析获得的滑坡滑裂面形态、失稳和运动特征与实际观察结果较吻合。潘万成等人[10]对滑坡地质条件、变形发育特征进行分析，并结合FLAC3D 数值模拟论证了滑坡的不稳定性，提出“地表排水＋抗滑桩＋格构锚杆”的综合治理对策。Li 等人[11]采用简化Bishop 法，分析了软弱层倾角变化下边坡稳定性变化规律，明确了软弱层对边坡滑移模式及稳定性的影响。Ávila 等人[12]以65 个滑坡为研究对象，利用物理模型FS FⅠORⅠ对可能影响边坡失稳因素进行了反演分析。Subramanian 等人[13]提出了一个空间分布和顺序耦合数值模型，模拟了融雪水诱发流域尺度的边坡失稳。该模型不仅能够较好地预测融雪水诱发滑坡的触发条件、震级和空间分布，而且具有较好的精度。影响滑体失稳运动的因素较多，但以坡表几何形貌作为影响因素，研究对滑体失稳特征影响的较少。因此，作者拟针对该影响因素，基于离散傅里叶逆变换的边坡坡表轮廓重构法，以颗粒单元组成失稳滑体，将未失稳坡体设置成为静止不动的墙体，准确生成非规则坡面的几何边坡模型，并导入PFC 2D 软件进行数值计算，通过设置监测颗粒和滑体分组，有效模拟了滑体颗粒在不同坡面轮廓下的运动轨迹，可为研究非规则坡面滑坡提供借鉴。

1 PFC 2D 工作原理及离散傅里叶逆变换

1.1 PFC 2D工作原理

与建立连续介质模型的有限元软件不同，PFC 2D 离散元软件以分子动力学为基本原理，建立非连续介质模型，软件的基本单元为相互独立的离散颗粒单元与墙体单元。本研究采用平行黏结模型，它包含5 个微观力学参数：切向黏结强度、法向黏结强度、切向刚度、法向刚度、黏结半径。每一个颗粒单元都能够在外力作用下独立运动，运动方式为转动或平移，颗粒间既能传递力，也能传递弯矩。基于FⅠSH 语言编写程序，分别给颗粒和墙体赋予不同材料参数，并在每个时步内更新单个颗粒、颗粒与颗粒、颗粒与墙体之间的速度、加速度、接触力等信息。当系统平均不平衡力与平均接触力之比小于1×10-5时，认为模型处于平衡状态。

PFC 2D 中，颗粒单元与墙体单元的循环计算如图1 所示。从图1 中可以看出，颗粒单元与墙体单元信息的更新计算是一个反复循环的动态过程，在每一个循环过程中，通过运用牛顿第二定律（运动方程），计算得到每个颗粒单元的合力及合力矩。同时，对每个接触使用力-位移方程进行求解，更新颗粒单元与墙体单元的位置信息，生成新的接触，如此不断循环计算并更新信息，直至模型达到平衡，计算停止。

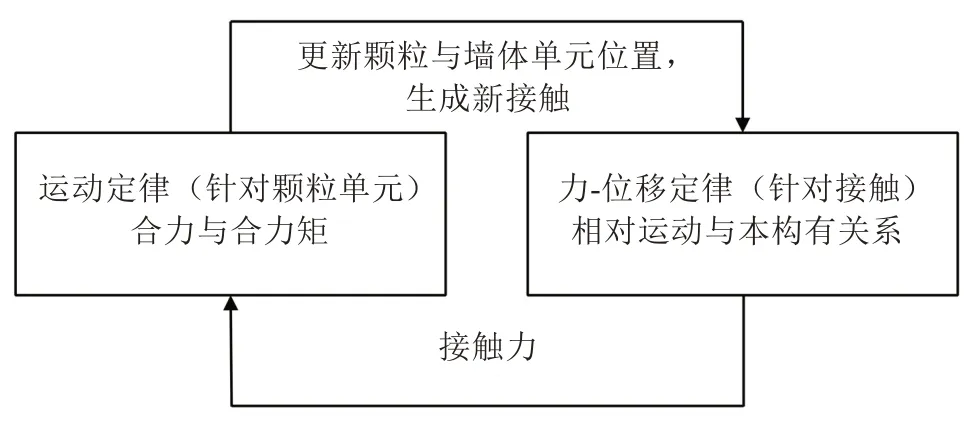
图1 计算循环示意Fig.1 Schematic diagram of calculation cycle

1.2 边坡坡表几何特征分析

以某路基边坡工程为例，对该坡表几何特征进行分析。该路基右侧边坡的边坡剖面线示意图如图2 所示。在图2 中，共5 条剖面线，利用GⅠS软件可分别得到相应的边坡剖面基线，本研究选取b、d 2条边坡剖面线进行分析。

图2 路基右侧边坡剖面线示意（单位：m）Fig.2 Schematic of the section line of the right side slope of the roadbed（unit:m）

剖面b、d 的边坡剖面基线图与剖面线起伏分量图如图3 所示。从图3 中可以看出，边坡剖面线上局部起伏特征明显，其中，图3中的剖面基线图中的直线是运用线性最小二乘法得到的整体坡度线，由此可以得到边坡坡面局部的起伏分量。边坡表面的非规则形态蕴含在该起伏分量中，即形态数据在一定水平（基线）上表现出有规律的波动。边坡剖面的起伏分量呈现多个频率的三角函数叠加特征，其中，低频成分较多，高频成分较少，而离散傅里叶正反变换分析法可以有效地描述这种规律性。因此，可基于离散傅里叶逆变换对非规则边坡轮廓进行重构。

图3 剖面b、d的边坡剖面基线与剖面线起伏分量图Fig.3 The slope profile baseline and profile line fluctuation component diagram of the section b and the section d

1.3 基于离散傅里叶逆变换的边坡坡表轮廓重构

在信号处理时，离散傅里叶逆变换（inverse discrete fourier transform，简称为ⅠDFT）具有将离散的频域信号合成为离散时域信号的特点。因此，坡表轮廓的生成过程中，可应用离散傅里叶逆变换的方法，将坡表轮廓视为时域信号，并将其基本公式[14]通过适当改写，可得到[15]：

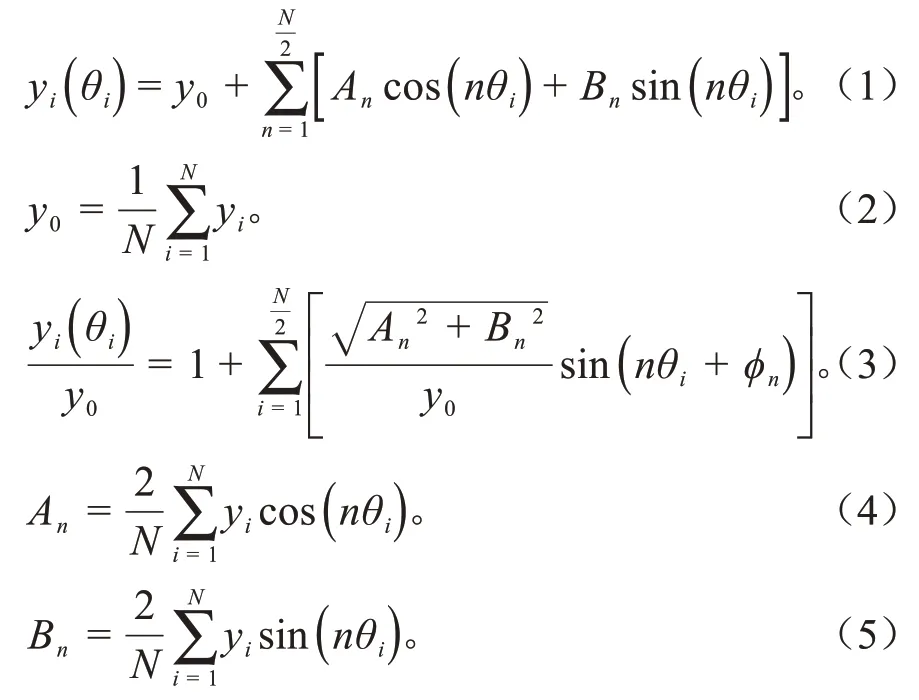
式中：n为谐波编号为谐波总个数；y为最终i通过离散傅里叶方法合成坡表轮廓在y方向的坐标值；y0为离散信号的均值；θi为坡表轮廓表达式的自变量；An和Bn为离散傅里叶正变换后得到的2个频域信号；ϕn为初相位；

由式（1）～（5）可知，当待分析的坡表轮廓线的离散点总数一定时，坡表轮廓线可完全分解为傅里叶描述因子Dn和初相位ϕn，n=1,2,3,…,64，二者均为无量纲数，即Dn和ϕn包含坡表轮廓线的全部几何特征。Dn本质上是三角函数的幅值，直接决定谐波的起伏程度（坡表轮廓线的主要形态），而初相位ϕn决定了各谐波在传播方向的平移情况。

1.4 傅里叶描述因子

根据文献[15]可知：傅里叶描述因子Di代表三角函数的幅值，其频谱整体为递减趋势，频谱分布情况大致为对数形式，可采用式（6）进行拟合。

其中，α=－1.40，β=－1.35，二者皆为无量纲的修正系数，D2、D3、D8为拟合公式中的自变量。

根据傅里叶描述因子对坡表几何形貌的控制作用，可以将傅里叶描述因子分为D2，D3→D7和D8→D64三大类。这三大类控制作用相应地由D2、D3、D8所决定，其中，D2控制坡面曲线较大的均匀起伏程度，D3控制坡面曲线较小的非均匀起伏程度，D8控制坡面曲线的最小起伏（即粗糙程度），如图4～5所示。

图4 D2与D3对坡面几何形貌的影响（D8=0）Fig.4 Ⅰnfluence of the D2 and D3 on slope geometry（D8=0）

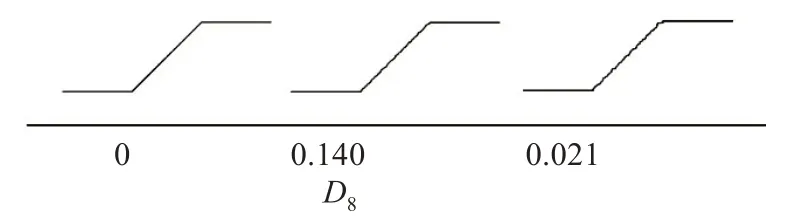
图5 D8对坡面几何形貌的影响（D2=D3=0）Fig.5 Ⅰnfluence the D8 on slope geometry（D2=D3=0）

2 坡表几何形貌对高位滑体滑移特性影响

2.1 模型建立

非规则边坡高位局部失稳滑动模型如图6 所示，采用参数t控制坡面角大小。坡面角t取值为38.7°，滑面段水平距离为2 m，坡面段水平距离为6 m，水平段长度为15 m。滑面段上方设有由墙体单元围成的矩形积土槽，用于生成并储存滑体颗粒，将滑体储存在简单矩形（二维）或长方体（三维）积土槽中。在数值模拟中，将非规则边坡高位处失稳滑体统一简化为矩形，所有墙体单元均保持静止不动。

图6 非规则边坡高位局部失稳滑移模型（单位：m）Fig.6 High-locality landslide model of irregular slope（unit:m）

生成的滑体模型如图7 所示，滑体长为2.56 m，高为1.2 m，生成的土体颗粒充满整个积土槽，颗粒总数为3 660 颗。为有效区分不同部位的滑体，在软件中编写命令语言，以矩形滑体形心为中心，将整个滑体平均分为4组，并以不同序号进行标记区分：上前部分滑体标为Ⅰ号，为第1 组；上后部分滑体标为Ⅱ号，为第2 组；下后部分滑体标为Ⅲ号，为第3组；下前部分滑体标为Ⅳ号，为第4 组。为选取滑体中具有代表性的颗粒进行分析，在矩形滑体的4个顶角处及中心位置，分别设置1个监测球，编号为1～5，用于监测该处颗粒的运动情况。

图7 滑体分组及监测球布置示意（单位：m）Fig.7 Schematic diagram of sliding body grouping and monitoring ball arrangement（unit:m）

2.2 数值模拟

由于傅里叶描述因子D2、D3、D8对坡面几何形貌具有不同控制作用，不同类因子的取值范围不同，Di取值过大或过小都会使得几何形貌失真，不符合实际情况。因此，在MATLAB 中生成大量的非规则几何形貌边坡，与实例的路基边坡工程中的边坡轮廓进行对比，经过多次试算与调整，使生成的非规则几何形貌边坡与实际自然边坡轮廓相似，从而确定合理的Di取值范围。其中，内摩擦角为5°～40°；坡面角为21.8°～90°；用于评判边坡稳定性无量纲系数γH/c为10，γ为土体重度，H为边坡高度，c为土体黏聚力；D2为0.100～0.280；D3为0.050～0.120；D8为0.007～0.021。

由确定的D2、D3、D8参数取值范围，采用控制单一变量的方法，保持初相位为定值，确定模型中D2为 0.100 或 0.250，D3为 0.050 或 0.120，D8为0.007或0.020。当D2、D3、D8皆为0时，整个坡表变为直线型。

先将MATLAB 生成的边坡轮廓数据点的坐标信息导入AutoCAD 中。再进行绘图操作，生成相应边坡轮廓图形。然后，将生成的边坡保存为dxf格式，导入PFC 2D 软件之中。最后，进一步编写命令生成组成积土槽的三面墙体，完成模型地建立。

将所有墙体摩擦系数设置为0，并在积土槽中生成滑体颗粒，初始颗粒之间接触选用线性接触，颗粒间摩擦系数为0，并赋予相应刚度，使生成的颗粒相互作用而弹开，最终充满整个积土槽。当积土槽中颗粒稳定后，摩擦系数重新规定，颗粒间定为0.25，而颗粒与墙体之间定为0.40。对于黏性土，再一次赋予颗粒之间的接触为平行黏结模型，对于无黏性土，颗粒之间仍保持线性模型不变。设置完接触模型后需要对模型进行再一次平衡，得到最终平衡后的模型参数取值。球的粒径比为1.50，密度为1 980 kg/m3；球-球的法向接触刚度为3 000 kN/m，切向与法向刚度比为1，摩擦系数为0.25；墙的摩擦系数为0.40；黏结模型（接触黏结）的法向黏结强度为5 000 Pa，切向黏结强度为5 000 Pa。

当滑体最终平衡之后，删除作为积土槽的墙体单元，让滑体在自重作用下变形解体，并沿着坡表向下运动，直到停止。

2.3 结果分析

为了研究坡面段几何形貌对滑体运动轨迹的影响，在滑体中设置5个监测球，监测并分析滑体4 个顶点和中心颗粒在不同坡面段几何形貌下的运动轨迹，每个编号颗粒的运动轨迹采用不同形式的轨迹线表示。

2.3.1 黏性颗粒的运动轨迹

直线型坡表中每个黏性颗粒的运动轨迹如图8所示。从图8 中可以看出，对于黏性滑体，编号1～5 的监测颗粒运动轨迹在直线型坡表呈现不同特征。3 号颗粒运动距离是最短的，表明：该处颗粒所受的阻力最大。1 号颗粒类似于抛物线型运动，表明：该颗粒没有受到其他颗粒的相互作用，即该颗粒的黏结接触破坏最早，随后颗粒沿着坡表运动。从整体上看，位于滑体上部颗粒的运动距离远大于位于底部颗粒的。

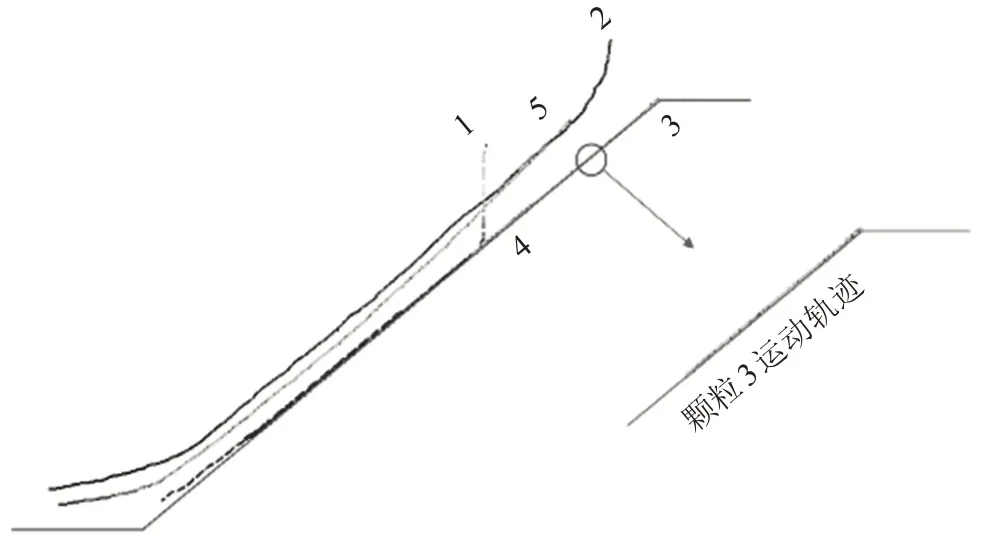
图8 直线型坡表黏性颗粒运动轨迹Fig.8 Diagram of the movement trajectory of viscous particles on the straight slope surface

D2类坡表中每个黏性颗粒的运动轨迹如图9所示。从图9中可以看出，随着D2的增大，监测颗粒的轨迹具有不同特征：4 号颗粒运动轨迹为均匀起伏型，D2越大起伏程度就越大；1 号颗粒先类似于抛物线型运动，然后与4 号颗粒一样沿坡表运动；2 号和5 号颗粒在坡面段运动轨迹类似于均匀起伏型，但与4号颗粒相比，起伏程度较小，随着D2的增大，起伏程度相应增大，相对于颗粒5平滑的运动轨迹，颗粒2的运动轨迹较为粗糙。

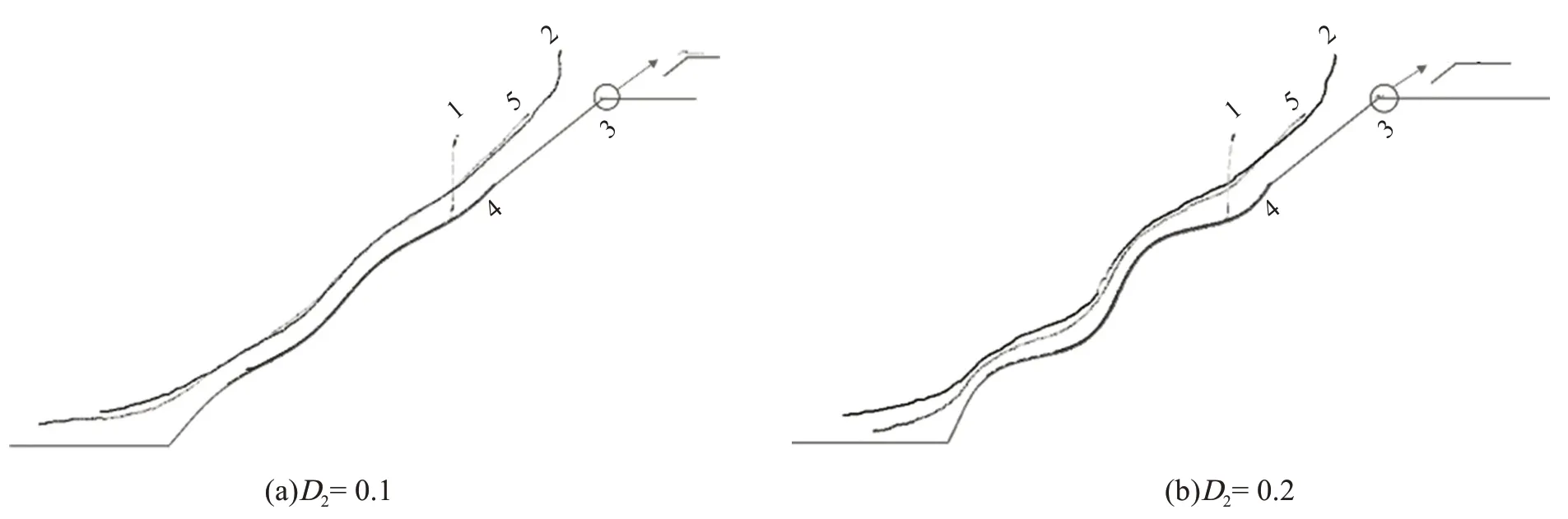
图9 不同D2下黏性颗粒运动轨迹Fig.9 Diagram of movement trajectory of viscous particles under different D2 conditions

D3类坡表中每个黏性颗粒的运动轨迹如图10所示。从图10 中可以看出，随着D3的增大，监测颗粒的轨迹具有不同特征：D3取值较小时（D3=0.05），4 号颗粒运动轨迹为非均匀起伏型，1 号颗粒先类似于抛物线型运动，随后变为非均匀起伏型；2 号和5 号颗粒运动情况类似，与4 号颗粒相比，均为程度较小的非均匀起伏型，颗粒2运动轨迹略为粗糙；D3取值较大时（D3=0.12），某一特殊几何形貌对颗粒运动轨迹影响较大，1 号颗粒做类抛物运动的距离增大，4 号颗粒在较大凹陷处运动轨迹脱离坡表，2 号和5 号颗粒在此处运动轨迹类似于直线型。

图10 不同D3下黏性颗粒运动轨迹Fig.10 Diagram of movement trajectory of viscous particles under different D3 conditions

D8类坡表中每个黏性颗粒的运动轨迹如图11所示，从图11 可以看出，随着D8的增大，监测颗粒的轨迹具有不同特征：当D8=0.02 时，4 号颗粒由于失稳时受到前方凸起坡表的影响，运动距离较短，最终停留在坡表凹陷处；1 号颗粒运动轨迹在坡面段为最小程度非均匀起伏型；2 号与5 号颗粒坡面段运动轨迹趋近于直线型，但2号颗粒轨迹线略微粗糙。

图11 不同D8下黏性颗粒运动轨迹Fig.11 Diagram of movement trajectory of viscous particles under different D8 conditions

2.3.2 无黏性颗粒的运动轨迹

直线型坡表无黏性颗粒运动轨迹如图12所示，与图8对比可知，黏性与无黏性颗粒运动轨迹并无很大差异，但也有不同之处。无黏性1号颗粒停留在水平段，黏性1号颗粒停留在坡面段，前者运动距离更长；无黏性2 号颗粒的运动距离比黏性2 号颗粒的短。

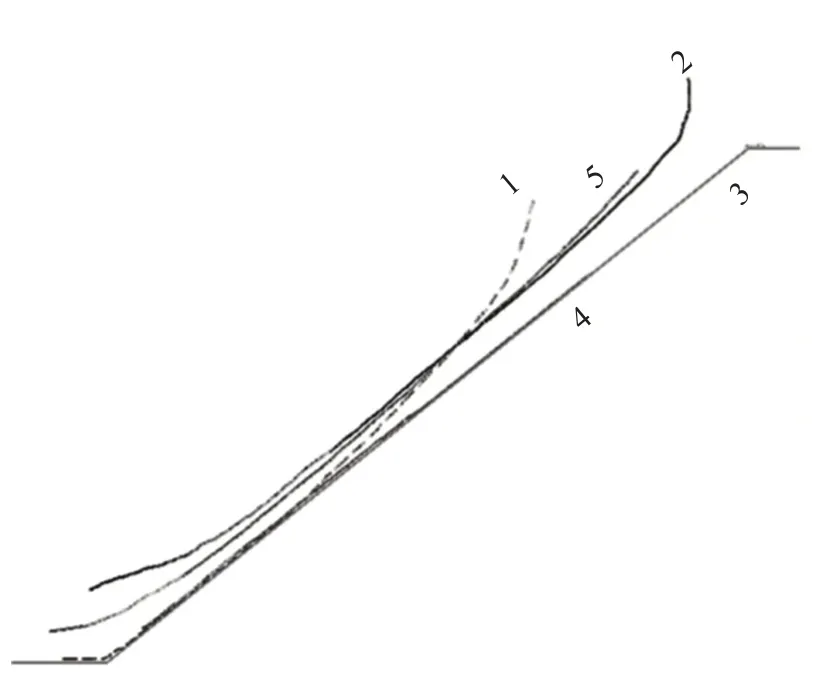
图12 直线型坡表无黏性颗粒运动轨迹Fig.12 Diagram of the movement trajectory of non-viscous particles on the straight slope surface

D2类坡表无黏性颗粒运动轨迹如图13 所示，与图9对比可知，两类监测颗粒运动轨迹相似，但也有不同之处。随着D2的增大，黏性1号颗粒与无黏性1号颗粒之间的运动距离相差越来越小；黏性2 号颗粒与无黏性2 号颗粒运动距离之差随着D2的增大而减小。当D2=0.2 时，两类颗粒运动距离大致相同，无黏性1号颗粒运动轨迹随着坡面均匀起伏程度的增大，而逐渐脱离坡表，在坡表上方运动。

图13 不同D2下无黏性颗粒运动轨迹Fig.13 Diagram of movement trajectory of non-viscous particles under different D2 conditions

D3类坡表无黏性颗粒运动轨迹如图14 所示，对比图10 可知，D3取值较小时（D3=0.05），两类1号颗粒运动距离基本一样。当D3取值较大时（D3=0.12），黏性1 号颗粒的运动距离明显大于无黏性1号颗粒的，这与直线型和D2类坡表明显不同。随着D3的增大，两类2 号颗粒运动距离相差越来越小。当D3=0.12 时，黏性2 号颗粒的运动距离反而大于无黏性2号颗粒的。当D3取值较大时，无黏性4 号颗粒由于特殊几何形貌的影响，其运动距离明显小于黏性4号颗粒的。

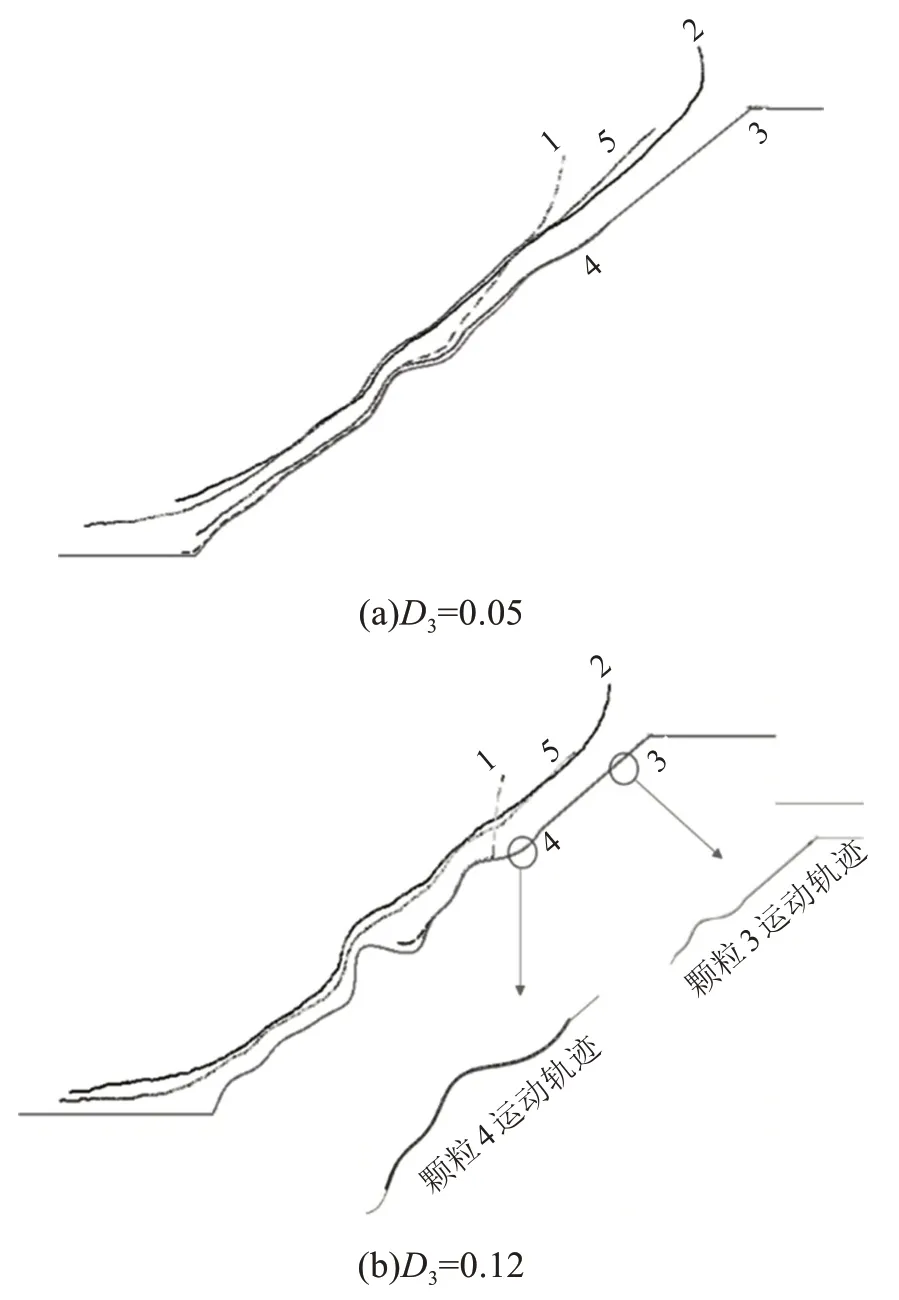
图14 不同D3下无黏性颗粒运动轨迹Fig.14 Diagram of movement trajectory of non-viscous particles under different D3 conditions

D8类坡表无黏性颗粒运动轨迹如图15 所示，对比图11 可知，随着D8的增大，两类2 号颗粒运动距离之差逐渐减小。当D8=0.02 时，黏性与无黏性2 号颗粒运动距离大致相同。两类1 号颗粒运动距离之差随D8的增大而减小，最终趋近于0。

图15 不同D8下无黏性颗粒运动轨迹Fig.15 Diagram of movement trajectory of non-viscous particles under different D8 conditions

对于黏性与无黏滑体，5 个监测颗粒运动轨迹在非规则坡表上各自特点：①当坡表为直线时，2号、4号、5号颗粒运动轨迹皆大致为直线，1号颗粒由于最先失稳且处于上前方，所以运动轨迹先为曲线型，再沿坡面运动成直线型。②当坡表为非规则几何形貌时，对1 号、2 号、4 号、5 号颗粒运动轨迹有较大影响，而对运动距离很短的3号颗粒可以忽略。滑体上方的1 号、2 号、5 号颗粒的运动距离明显大于位于底部4号颗粒的。

坡面几何形貌对不同土类滑体的运动轨迹影响也不相同。对于D2类坡表，随着D2取值的增大，无黏性1 号颗粒的运动距离逐渐趋近于1 号黏性颗粒的，2 号颗粒的运动规律也是如此，且无黏性1号颗粒随着D2的增大而略微脱离坡表运动，这是由于无黏性土内部颗粒间没有黏聚力，整体性较差导致的。对于D3类坡表，D3较小时，两类颗粒运动距离基本相同，但继续增大后，由于坡表存在较大凹陷与凸起处，导致黏性颗粒的运动距离将大于无黏性颗粒的。对于D8类坡表，当D8取值较大时，黏性与无黏性的1 号、2 号颗粒的运动距离大致相同。

3 结论

基于离散元软件PFC 2D，对非规则边坡高位滑体失稳模型进行数值分析，同时，基于离散傅里叶逆变换分析得到三类傅里叶描述因子Di对边坡坡表几何特征的影响规律，研究讨论了不同傅里叶描述因子取值条件下的坡表轮廓对黏性与无黏性滑体失稳运动特性的影响，得到结论为：

1）整体分析表明，D2、D3、D8三类傅里叶描述因子不同取值形成不同类型的非规则坡面，而且坡面非规则几何形貌对黏性与非黏性滑体的失稳运动特性都有明显影响。

2）坡面非规则几何形貌对下前方的4 号颗粒运动轨迹影响是最大的，1 号颗粒也受到坡面几何形貌的影响，2 号、5 号颗粒运动轨迹受到坡面几何形貌的影响相对较小，这是由于2 号、5 号颗粒所处位置较高且靠后的原因。因此，颗粒所处的位置越靠后、越高，其运动轨迹所受坡面几何形貌的影响越小。

3）对于相同坡表，黏性与无黏性滑体内部5个监测颗粒运动轨迹相似，但也有部分差异。对于取值较大的D3与D8类坡表，某一特殊的几何形貌出现在特定位置会对颗粒运动轨迹产生较大影响，而D2类坡表由于坡面几何形貌均匀起伏，因此不会出现这种现象。