基于固定接触约束的多指灵巧手动力学建模*

余 进 ，张红俊

（1.长安大学公路养护设备国家工程实验室，陕西 西安 710065；2.重庆长安工业（集团）有限责任公司，重庆 401120）

0 前言

多指灵巧手作为一种末端执行机构具有高自由度、高灵活性的特点，能够完成多种精细、复杂的操作，在工业加工[1]、家庭服务[2]、太空探索[3]、康复医疗[4]以及危险品处理[5]等领域都有不错的应用前景。在各种操作任务中，多指灵巧手需要通过与被操作物体进行接触来调整物体的运动状态，该过程中不同的接触方式会产生不同的操作效果。文献[6]将任意两物体间常见的接触分为点接触、线接触以及面接触，其中点接触在操作灵活度上更具有优势。常见的点接触中，固定点接触方式在实际操作应用中较为常见且其理论上受到的运动约束最为简单，便于研究。

目前，在对多指灵巧手进行动力学建模的研究中，大部分动力学模型只针对多指灵巧手进行了动力学建模，未对灵巧手与被操作物体间的接触约束进行考虑，如文献[7]和[8]提出通过Newton-Euler方法表示出单指的动力学方程。Udwadia-Kalaba方法[9]的优势在于无须引入额外的变量且适用范围广泛。文献[10]中，赵晓敏等人对比讨论了U-K方法相较于Lagrange方法和Newton-Euler方法的优缺点。

本研究中主要包括以下三个方面的工作：第一部分简要对Udwadia-Kalaba理论进行介绍；第二部分对灵巧手手指和物体在固定点接触时进行运动学分析；第三部分使用层级堆聚建模方法对多指灵巧手和被操作物体整体进行动力学建模并对该系统模型进行仿真。

1 Udwadia-Kalaba理论

若一个机械系统由s个质点或刚体组成且可以通过广义坐标向量q∈nℝ来表示该系统在任意时间t的位移，则在不受约束条件下的系统运动方程可表示为：

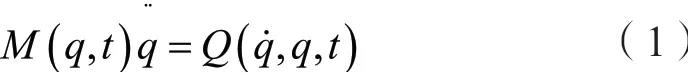
式 中M(q,t)∈ℝn×n为 系 统 的 质 量 矩 阵，为系统所受到的给定力。若该系统受到l（l＜n）个约束，其所受约束的Pfaffian形式可表示为：

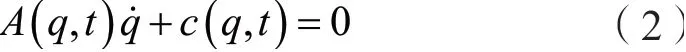
式中A(q,t)∈ℝl×n，c(q,t)∈ℝl。对式（2）进行求导后可得到二阶形式为：

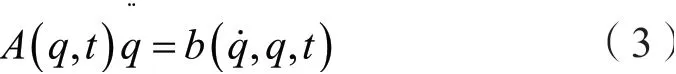
假设1：机械系统质量矩阵M(q,t)正定且对称。假设2：约束方程式（2）中的矩阵A(q,t)满足Rank(A)≥1。

定理1[11]：满足假设1～2的机械系统式受到约束时，机械系统的运动方程可表示为：

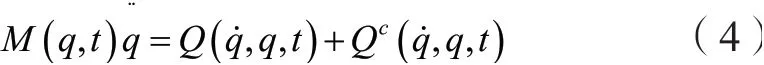
定理1给出的系统运动方程在质量矩阵满秩的情况下，能够适用于完整约束和非完整约束条件下。

2 接触分析

三指灵巧手的结构如图1所示，将固连在三指灵巧手手掌上的坐标系设为基坐标系，取用于描述第i根手指的广义坐标，为描述被抓取物体的广义坐标。若灵巧手单根手指与被抓取物体之间产生固定接触时，将满足一个约束，即手指指尖与物体在接触点处的位置相等[12-15]。

图1 三指灵巧手

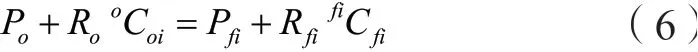
上式中，Po∈ℝ3、Pfi∈ℝ3分别为物体坐标系原点和指尖坐标系原点在基坐标系下的位置向量，oCoi和则分别为物体坐标系和指尖坐标系下接触点的位置向量。对式（6）求导可得：

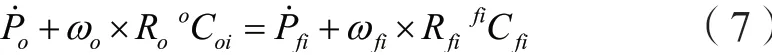
将系统所受到的约束方程式（7）整理成矩阵的形式为：

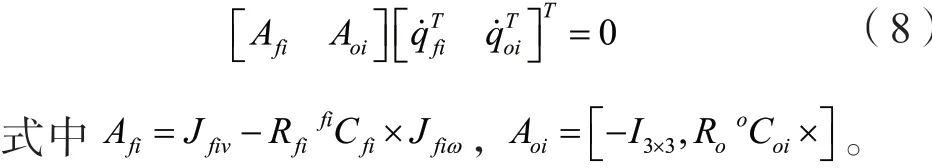
3 抓取系统动力学建模

将多指灵巧手分为四个子系统，即三个单手指子系统和被抓取物体子系统。假设单手指系统的各个连杆均为均质杆且手指运动不受摩擦力的影响，则根据Lagrange方程，单手指子系统的动力学可表示为：

式中Mfi∈ℝ6×6为单手指子系统的质量惯性矩阵，Qfi∈ℝ6则为该子系统所受到的科氏力和重力。同理，被抓取物体子系统的动力学可表示为：

式中Mo∈ℝ12×12为被抓取物体子系统的质量惯性矩阵，12

oQ∈ℝ为该子系统所受到的科氏力和重力。结合式（9）和式（10）可得到多指灵巧手在“未受约束”下的动力学方程可表示为：

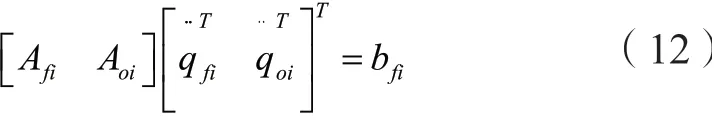
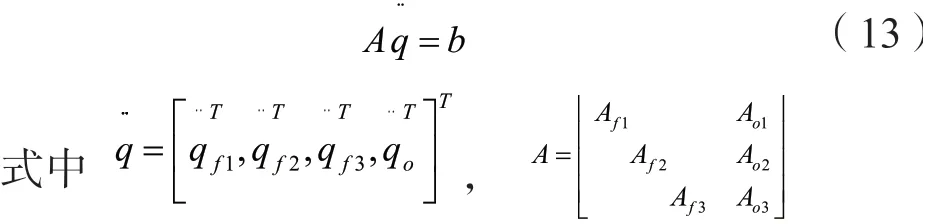
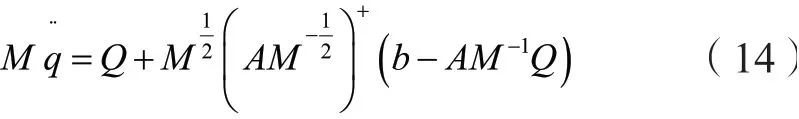
4 总结

本研究首先对Udwadia-Kalaba方法进行简要介绍，随后对灵巧手与物体间在固定接触下的运动进行分析，表示出其在空间中所受到的约束方程，然后基于层级堆聚建模方法，在对单手指和物体进行分别建模之后，基于Udwadia-Kalaba方法利用接触约束建立灵巧手与被抓取物体的整体模型，为后续对抓取系统的控制器设计提供准确的模型基础。