加载路径对副车架成形结果的影响分析**

刘邦雄

（景德镇学院机械电子工程学院，江西 景德镇 333000）

0 引言

近年来，随着新能源的推广，各大厂商都在寻求减轻汽车重量的路径，轻量化已成为汽车的一个重要研究内容，人们开始更多地去关注减轻汽车重量，减少能源消耗，降低二氧化碳排放量[1-4]。

减轻汽车重量的主要方式为材料的选择和工艺优化。内高压成形主要是从工艺上开展优化，与传统加工工艺相比，可以有效地减少模具的使用，简化工序，节省材料。最早是由国外学者在20世纪40年代提出的，经过不断的研究，已经在成形机理、实验研究等领域取得一些进展[5-6]。刘晓晶等[7]对副车架的截面进行了主要分析，主要有矩形、梯形、多边形等，针对其难成形、轴线为空间曲线、易破裂等问题进行了研究，通过AutoForm软件模拟得出最大增厚及最小减薄位置处，对成形参数作了优化，并通过实验加以验证。李鑫等[8]以副车架为研究对象，设计了多工序成形工序，针对成形结果中出现的破裂等现象进行了优化，采用响应面法对压力、初始屈服压力以及轴向进给量三个参数进行了优化。王磊等[9]对扭转异形管件进行了研究，针对其成形扭转角度困难的情况进行了理论研究，在内压力和压力的作用下共同成形，并通过实验验证，回弹较小，壁厚分布较为均匀。黄煜等[10]以三元催化器端盖为研究对象，提出一模两件的工艺方法，对端盖成形关键因素进行分析，起皱数量过多或过少都会对成形质量产生影响，起皱数量适中能够获得成形质量较好的零件。崔晓磊等[11]研究了不同加载条件对管件尺寸精度的影响，通过在模具内侧布置传感器检测位移量记录加载位移。内压力增大会产生一定回弹，提出调控精度的工艺参数方法。笔者以副车架加强梁为研究对象，借助有限元成形软件，研究不同加载路径对成形结果的影响，为副车架成形提供有益参考。

1 数值模拟

1.1 有限元模型的建立

副车架加强梁如图1所示，由两块钣金冲压焊接而成，两侧焊缝各为4条，由5个安装孔组成。传统成形工序繁多，而副车架为典型变截面零件，符合内高压成形要求。为此，将管件预成形，弯曲一定角度后导入模具中。如图2所示，1为上模具，2为下模具，3为预弯管件，将弯管件3置于上下两模具之间，封闭两端冲头，通过液压油胀形而成。从图中可以看出，管坯均匀放置于上下模具中间，未发生模具干涉，为检验合模过程能够替代预成形工艺，需对合模后的管坯件进行结果测评，判断预成形是否出现破裂或者起皱现象，为内高压成形奠定基础。预成形结果如图3所示，从图中可以看出，预成形效果较好，减薄率为18.8%，增厚率为16.2%，其结果与弯管后对比没有发生太大区别，停留在膨胀率合理区间内，其合模成形结果的减薄率和壁厚满足后续胀形要求。

图1 副车架加强梁数模

图2 CAE仿真模型

图3 预成形结果

预成形极限图如图4所示，从图中可以看出，主次应变均发生在安全区域以内，未超出临界区，且离临界区还有一段距离，能够继续开展下一步内高压成形过程的数值分析。

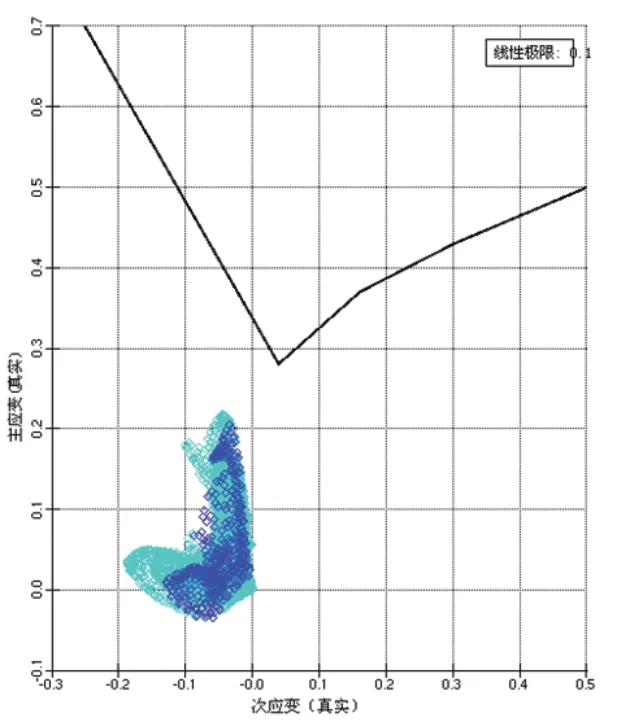
图4 预成形极限图

1.2 主要工艺参数的确定

初始屈服压力是指材料开始发生塑性变形的临界值。内高压成型初始屈服压力可以根据Tresca屈服准则理论公式来计算，公式如下：

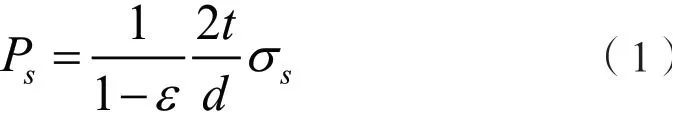
其中：sP——屈服极限压力，单位MPa；ε——轴向力与环向力比值，无轴向进给或简便计算值设定为0；t——管坯的厚度，单位mm；d——管坯外径，单位mm；sσ——材料屈服强度。计算得出屈服压力为42.4 MPa。

整形压力为管坯已完成塑性变形后，管坯外表面大部分与模具完成贴膜，但部分复杂区域还需要更大的压力，使管坯全部贴合模具。在不考虑轴向进给和加工硬化情况下，整形压力公式如下：

其中：cP——整形压力，单位MPa；t——过渡圆角处壁厚，单位mm；cr——最小圆角，单位mm。计算得出整形压力为216 MPa。

极限开裂压力为无轴向进给时，进行管坯内高压纯胀形时发生破裂的压力。简化公式如下：

其中：bP——极限开裂压力，单位MPa；bσ——抗拉强度，单位MPa。管坯抗拉强度为440 MPa，计算得出无轴向进给开裂压力为58 MPa。

轴向进给力是保证管件密封和关键塑性变形的关键参数，由三个部分组成管件，保持塑性所需压力，克服管壁与模具间的摩擦力，高压液体产生压力。工程中快速估算轴向进给力理论公式如下：

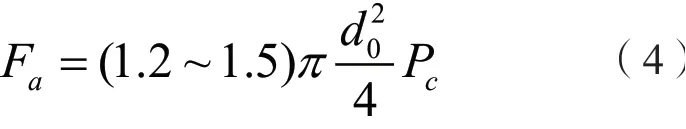
其中：aF——轴向进给力，单位N；d0——管坯初始内径，单位mm。推出轴向进给力为604 kN～700 kN。

合模压力是指上下模具在液压成形工艺过程中需要的模具压力。计算公式如下：

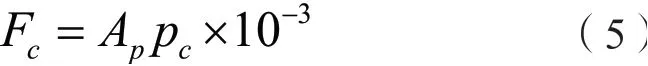
其中：cF——合模力，单位kN；pA——成形零件水平面投影面积，单位mm2。计算得出合模力为6 245 kN。

1.3 加载路径

成形过程中内压力会持续上升，上下模具和弯管之间的摩擦力也增大，轴向进给力呈现非线性变化，不同加载路径对成形结果影响较大。采用单因素变量法研究不同轴向进给加载路径对壁厚的影响。图5为不同加载路径，（a）为两端冲头都线性轴向加载，（b）（c）为不同折线加载路径。

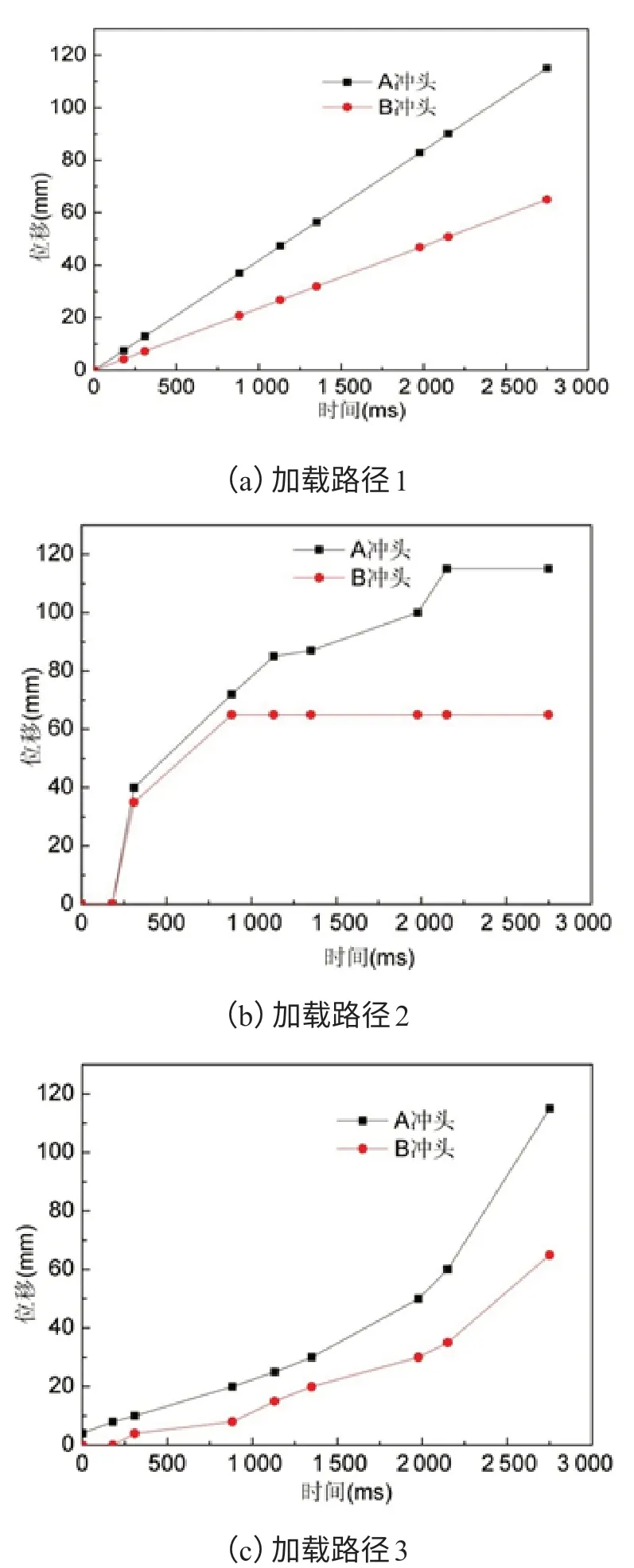
图5 不同轴向进给加载方式

2 成形结果

表1 为不同加载方式下成形壁厚结果，从表中结果可以看出，加载路径2的壁厚差最小，壁厚成形较为均匀，壁厚差为1.576 mm。加载路径1壁厚变化比较大，在加载方式1成形下的结果显示，最小壁厚为1.223 mm，最大壁厚为4.161 mm，壁厚差为2.938 mm，局部产生起皱现象。在加载路径3成形下的结果介于加载路径1和加载路径2之间，壁厚差略大于采用加载路径2成形下的结果。综上，选择加载路径2的方式进行轴向进给的加载，其成形极限图如图6所示，从图中可以看出，副车架加强梁没有发生破裂、起皱现象，壁厚分布较为合理，整体处于安全区域内。

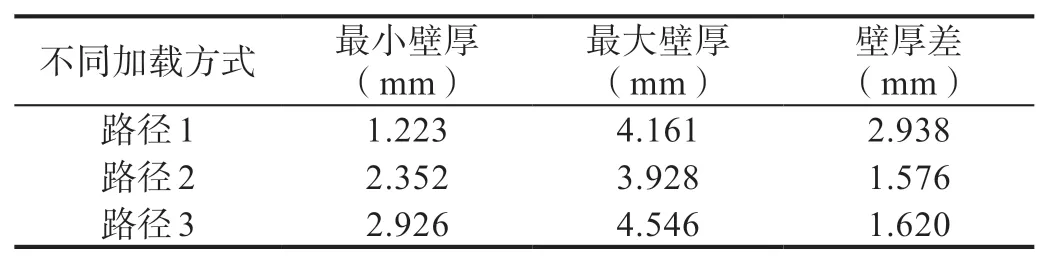
表1 不同轴向进给加载方式下成形壁厚

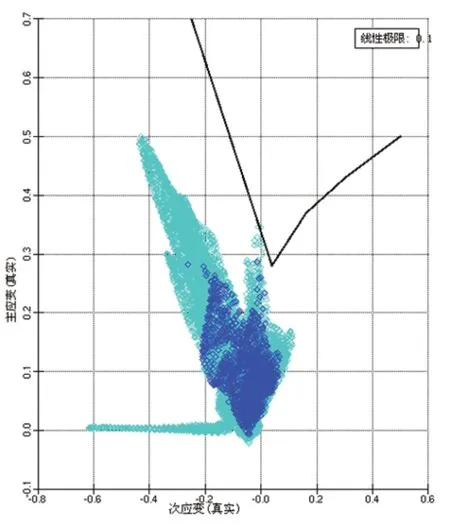
图6 成形极限图

3 结论

本文采用单因素变量法，通过壁厚分布探究不同轴向进给加载路径对成形结果的影响，结果表明折线加载路径效果较好，从成形极限图中也能看出采用折线加载路径下成形效果较好，加强梁没有发生起皱、破裂等现象。