含间隙平行四杆收回机构的非线性动力学分析**
马一帆 ,陈 强 ,潘佳煊 ,虞 浪 ,钱孟波
(浙江农林大学光机电学院,浙江 杭州 311300)
运动副两构件元素之间不可缺少的介质空间被称为运动副间隙,此处介质可以为空气、润滑油甚至真空,运动副间隙是机构间可以进行相对移动、机械系统自由度不为零的必要条件。此外,由于制造加工与装配误差、机械刚性或柔性变形、热变形等问题也会造成间隙值在一定范围内变化[1]。因此,在设计中通常采取设定公差的方式对运动副间隙的存在进行提前考虑。
间隙运动学是由现代先进机械对高位置精度、高运行速度、高工作强度、高可靠性、高经济性以及复杂多变的工作环境等要求共同促成的,已经成为力学、机械工程、航空航天工程、车辆工程等众多理工科领域的研究热点[2]。间隙运动学在很多领域是多体动力学发展的进一步延伸,例如文献[3],对于机构的虚拟样机预测在考虑运动副间隙以后会变得更加准确合理,同时也揭示了含间隙多体动力学系统的突出特征是变结构、含碰撞、非线性、非连续。本文将间隙运动副理论引入农业机械的平行四杆深度调节机构中用于提高机械的设计精度,使用Poincare理论对结果进行混沌现象的定性[4],再对具有混沌现象的非线性结果进行分析,分析出设计中重要的角度值与公差值[5]。
1 主要工作内容
1.1 工作内容概况
本文选取农用机械中的平行四杆深度调节机构为研究对象,主要工作内容分为两个部分:一部分是基于Adams软件平台进行的含间隙运动副函数子程序二次开发,一部分是平行四杆深度调节机构的模型创建、仿真及结果分析。主要步骤如图1所示。
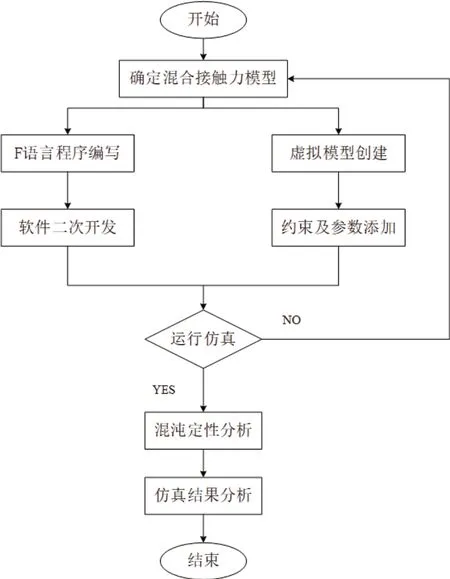
图1 含间隙分析流程图
1.2 含间隙运动副混合接触力模型选取
从20世纪70年代开始,国内外学者为了能够精准描述运动副间隙在实际工作中的运动状态,建立了一系列间隙运动学模型。依据经验,一般将法向接触力模型分为三类:间隙运动副连续接触模型[6]、间隙运动副经典碰撞模型(三状态模型)[7-8]、间隙运动副连续接触力模型(二状态模型)[9]。
本文采用二状态间隙法向接触力模型进行子程序二次开发,间隙运动副连续接触力模型将间隙运动副构件间的彼此运动状态根据边界条件分为自由分离阶段和接触碰撞阶段两类,所以又称为二状态模型。与三状态模型相比最显著的特征是所划分的运动状态少了一个,但最本质的区别则是建模所基于的平衡方程参数不同。二状态模型基于力的约束来构建平衡方程,每次构件的相互接触在开始和结束的时刻,其接触位置的接触力和形变量都为零,且过程中两个量连续变化。该类模型的接触区域是柔性的,穿刺深度和接触力成非线性函数关系,可以计算出阻尼力、摩擦力、接触力、形变速度、形变量等数据,是目前应用最多的间隙动力学模型。因此,本文选择二状态模型中使用较多的L-N模型对平行四杆机构进行含间隙动力学仿真。
这类模型同时也存在着缺陷。一方面,需要频繁地判断接触的发生与接触类型,使得用于计算的数值方法必须在保持收敛的条件下具备高精度结果和高计算效率。另一方面,这类模型的计算精度并没有三状态模型精确。但对于难以计算界定临界状态的三状态方法和较为古老的经典模型而言,二状态模型无论在计算效率还是结果精度上都有无法比拟的优势。

其中,δ˙(-)为初始碰撞速度,K为接触刚度,ce为恢复系数,δ为穿刺深度。
关于混合接触力模型中切向接触力的部分。本文的含间隙碰撞接触力模型中切向力部分沿用了经典的库伦接触力摩擦模型,此种模型的主要影响变量是法向接触力和摩擦系数。但是该模型用于本文的接触力模型计算中是存在问题的,上文已经说明在二状态模型中位移和力是处于连续变化状态的,但是库伦模型存在不连续性,在高频接触-分离中大量的离散数据点导致数值计算收敛性降低[10]。另外,随着摩擦研究的发展,学者发现库伦模型对材料属性、外界影响、黏滑现象考虑不足,会导致计算结果存在偏差[11-12]。虽然众多学者在此方面进行了研究,但是目前没有一个完善的方法,需要进一步研究。
1.3 含间隙平行四杆机构模型创建
进行构件含间隙动力学分析首先必须进行间隙运动副子函数的二次开发,其过程分为四个步骤:
第一步:编写F语言程序,模板程序中主要包含五个部分,外部变量定义、局部变量、参数定义、可执行代码、将可读的变量名分配给传递的参数并调用SYSARY采集参数。
1)外部变量定义模块为定义变量在计算机中储存位置和储存格式的模块。外部变量定义模块如图2所示。

图2 外部变量定义模块
2)局部变量为实现设定好的计算变量,一部分的具体数值只可在程序中进行修改,包括π值、指数e等。另一部分是计算中出现的定义变量,包括两构件尺寸、穿刺量、接触点位置角等。
3)参数定义模块与导入Adams后的用户输入参数界面相对应,包含18个需要在仿真前用户根据所计算运动副情况自主输入的变量值,包括孔轴构件的模型编号、孔轴半径、法向接触力等。
4)可执行代码为程序段的核心内容,其中包括了二维、三维接触及摩擦速度的判断代码,摩擦模式的判断代码,轴向接触力、径向接触力、摩擦力计算代码等核心代码。
5)将可读的变量名分配给传递的参数,调用SYSARY采集参数模块为功能模块,主要服务于计算程序中变量名的传递和数据赋值。
第二步:使用VS平台对编写的gfosub.f程序包进行编译,并将编译后形成的gfosub.dll文件加载进入Adams的函数库完成对运动学仿真平台的二次开发。VS平台编译窗口如图3所示。编译过程如下。

图3 VS平台编译窗口
1)首先需要编译完成的f代码,得到目标文件(*.obj)。然后还需生成动态链接库文件(*.dll)。
2)将生成的dll文件加入到Adams库中。
第三步:在Solidworks平台中进行对象建构,也就是平行四杆深度调节机构的三维模型建立工作,并将其导入至Adams平台中添加约束与驱动,播深调节机构模型如图4所示。此处需要使用自主编写的子函数间隙旋转副替代软件平台中自带的旋转副函数,主要步骤是在运动副销构件轴向两端中心点添加一对一般力矢量并在孔轴构件之间添加相互作用力。将仿真设置中执行栏目下的求解库改为C:/mysubroutine/gfosub.dll,并将一般力矢量的定义使用改为“子程序”,此时可以在用户参数输入根据程序定义输入对应计算参数量。一般力矢量用户参数输入界面如图5所示。

图4 播深调节机构模型

图5 一般力矢量用户参数输入界面
第四步:仿真参数设置,此处需要设置的仿真参数主要为仿真步长、仿真阶数、最大迭代次数等变量。
2 结果与讨论
2.1 含间隙平行四杆机构运动混沌现象
Poincare映射是对运动及动力学数据是否具有混沌现象进行定性分析的重要方法[4],混沌理论描述了物体运动的不可预测性,对非线性系统意义非凡,产生混沌现象表明系统的稳定性受到影响。因此,本文使用Poincare映射对加入间隙后的深度调节机构角加速度数据结果和X方向轴心轨迹结果进行分析,佐证在机构运动中考虑间隙的科学意义。
Poincare映射指多维相空间中选取一个适当截面赋予共轭状态变量,此截面称为Poincare截面,将各Poincare截面点作为离散点进行串联,观察形成的相轨迹线即可找出系统运动学特性。对于作周期运动的机构运动而言,在各个周期的相同时刻进行取点,将一个周期作为一个Poincare截面,选取的时刻与对应变量组成共轭状态变量绘制图形。本文分别对角速度(图6a)和X方向中心点位移(图6c)进行Poincare映射图绘制,由于Poincare映射对周期数具有一定要求,将仿真进行了120周期运行,每周期约2 500个数据点,选取每个周期的第1 500个数据点作为Poincare截面,各点组成共轭状态量(xk,ωk)与(xk,Xk),其中k表示周期数,x表示对应时间点坐标,ω表示对应角速度坐标,X表示对应位移坐标。除折线连接以外使用6次多项式对共轭点进行拟合绘制,如图6(b)与图6(d)所示。
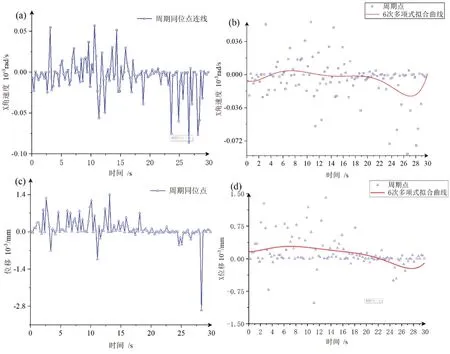
图6 Poincare映射图
从上图可以看出,无论是位移还是角速度的Poincare映射结果折线图都不在一条直线上,6次多项式拟合结果也显示多项式系数与首项系数偏差较远,不是线性拟合曲线,这表明在加入间隙后仿真结果不具有周期解,运动中出现混沌现象。
2.2 旋转副间隙大小及转速对动力学特性的影响
间隙值是影响机构动力学表现的重要参数之一,图7是在变间隙的影响下,以固定0.125 r/s的驱动速度进行仿真计算,去除了最初5个数据点并对数据点进行等间距取值后的Y轴映射结果图。从图中可知,运动副间空间的存在加大了启动阶段的运动副非线性变化,尤其是前1.25 s时间段内。此后,运动的波动明显减小,说明在机构行进角度至56.25°之后,两运动副元素由于垂直地面作用力的关系,相互运动空间被压缩,力的非线性变化程度可以被认为是相互运动自由程度的一种表现,此后的运动将存在卡死的风险,尤其是在运动角度α大于75°,也就是运行至1.5 s时,力的非线性度降低和接触力整体提升进一步加剧。
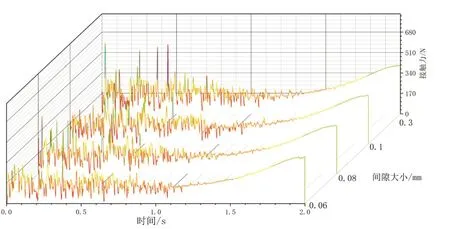
图7 间隙对接触力的影响图
由以上数值计算结果可得,在设计过程中,将α设置为60°较为合适,间隙值控制在0.1 mm附近时对机构的动力学影响较小,也不会造成成本的过度增加。
图8 是间隙大小为0.1 mm,驱动速度设为0.125 πrad/s~1 πrad/s时,销轴的轴心三维运动轨迹图像,其中Z轴方向是销轴的运动轴向,X轴和Y轴是销轴的运动径向,为便于观察轨迹圆的径向运动图形,对三维轨迹的径向进行投影,在底面绘制二维轨迹圆。
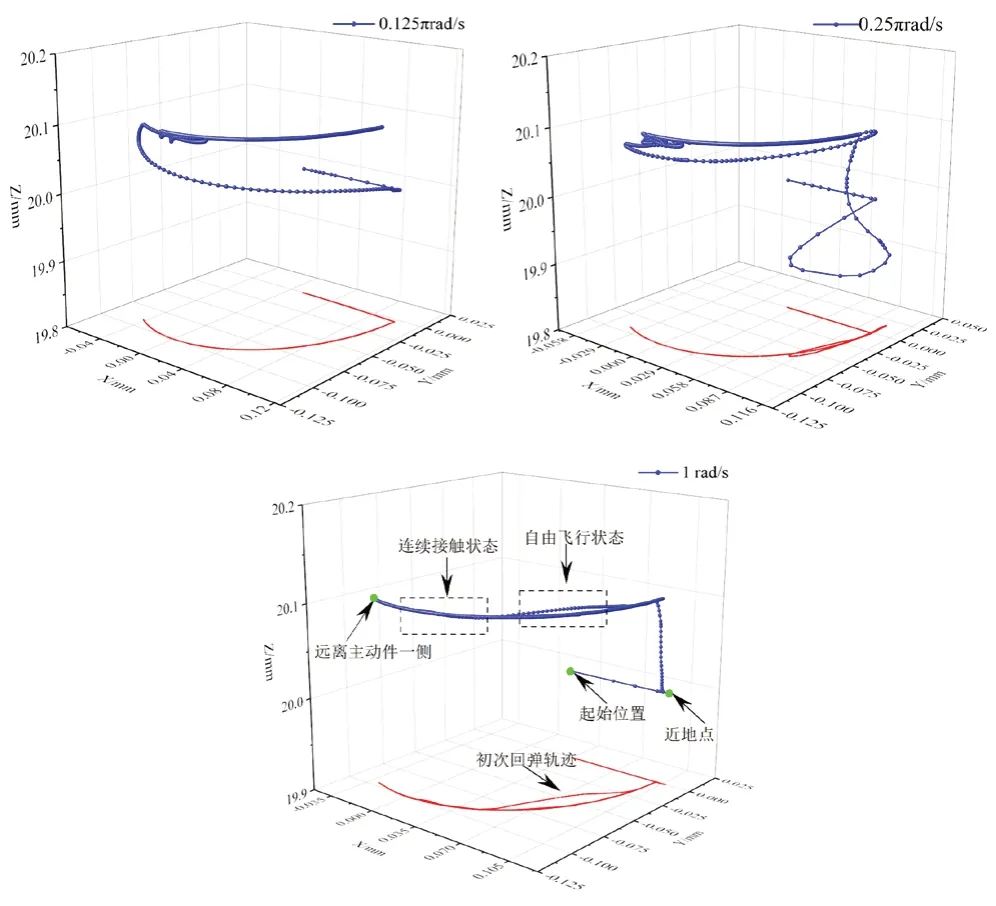
图8 不同运行速度下销中心点的空间运行轨迹图
从图中可以看出,驱动速度的不同不会影响整体的运动趋势。第一步,销构件受重力作用下坠,与孔构件在垂直方向底部首次碰撞并发生回弹。第二步,由于主动件传力的作用,轴心点移动向远离主动件一侧,背离主轴移动。第三步,在所受合力及惯性的作用下,轴心点移动接近近地点,期间两构件连续接触。驱动速度的增加将导致初次回弹轨迹幅度加深,表明了初次碰撞激烈程度的提升。设定极限强度时必须考虑设计的理论运行速度,同时,由于更大的驱动速度将带来更大的穿刺量,且最大穿刺必定发生在相对固定的位置,因此会对轴销构件的圆度产生较大的影响。
3 总结与展望
在考虑了运动副间隙以后,可以明显地观察到平行四杆深度调节机构的运动学特性和动力学特性出现了难以控制的非线性特征。由于使用了二状态模型进行仿真,可以直观地展现力的变化和穿刺现象。通过分析结果可以得到以下结论:
1)考虑间隙后,机构将产生非线性振动现象,经过本文的定性证明,含间隙机构的振荡具有混沌现象的特点。
2)为保证机构工作的可靠性和机械制造的经济性,平行四杆深度调节机构的间隙公差应控制在0.08 mm左右。
3)平行四杆机构活动角α设计为60°是合理的,可以将构件的位置精度误差控制在一个合理的范围内,避免机构卡死的发生,同时小于90°,不改变设计的运动趋势。
4)本文的结果证明,运行速度和间隙值对机构的起始阶段影响最为显著,集中表现在初次碰撞时的穿刺量和碰撞接触力,这对设计运行速度和构件的圆度公差提出了特别的要求。
5)完成了含间隙运动学分析的全过程操作,包括了混合接触力模型的选取建立、模型程序包编写、子程序函数包二次开发、机构虚拟模型创建及仿真、结果混沌定性分析以及参数的设计。
但是本文的研究使用的所有构件均为刚性结构,没有对构件的宏观变形进行考虑,需要进行下一步研究完善。

