圆形有界磁场中“磁发散”与“磁聚焦”规律的探析

湖南 王跃军

带电粒子(不计重力)在圆形有界磁场中的运动问题，在高考及物理竞赛中频繁出现，该类题型通常情境新颖，较好地综合了物理、数学知识，着重考查学生的综合分析能力，逻辑推理能力，以及应用数学知识解决物理问题的能力。而当磁场圆半径等于轨迹圆半径时，有如下两条规律。磁发散规律：如图1所示，若带电粒子从圆形有界磁场边界某点沿不同方向射入磁场，则粒子射出磁场时速度方向都相同，且与入射点处的切线方向平行。磁聚焦规律：如图2所示，平行射入圆形有界磁场的带电粒子，都将从磁场边界的同一点射出磁场，且粒子的入射速度方向一定与出射点处的切线方向平行。

图1 图2

磁发散规律的证明：

如图3所示带负电的粒子(不计重力)从圆形有界磁场O1边界上的A点射入磁场，AD为过A点的切线，已知粒子在磁场中圆周运动的轨迹圆O2的半径与磁场圆O1的半径相等。若粒子经磁场偏转后从磁场边界的C点沿CE方向射出。下面来证明CE∥AD。

图3

连接O1A、O1C、O2A、O2C，由于磁场圆半径等于粒子轨迹圆半径，故四边形AO1CO2为菱形，因而可得：

O1A∥O2C①

AD为磁场圆过A点的切线，则有：AD⊥O1A②

由①和②可得：AD⊥O2C③

CE为粒子在磁场边界C点的出射方向

CE⊥O2C④

由③和④可得：CE∥AD

由于粒子从A点射入磁场的方向是任意的，而A点的切线方向是确定的，故从A点射入磁场的所有粒子都会平行于AD方向射出，如图1所示，粒子的入射方向是分散的，但经过圆形有界磁场偏转后，转变成平行方向射出，这类比于光学中，经过凸透镜焦点的入射光线经凸透镜折射后变成平行光线。同理亦可证明磁聚焦规律。

下面笔者通过三个例题探析规律的应用。

【例1】电子质量为m，电荷量为e，从坐标原点O处沿xOy平面射入第一象限，射入时速度方向不同，速度大小均为v0，如图4(甲)所示。现在某区域加一方向向外且垂直于xOy平面的匀强磁场，磁感应强度为B，若这些电子穿过磁场后都能垂直射到荧光屏MN上，荧光屏与y轴平行，求：

(1)荧光屏上亮线的长度；

(2)所加磁场范围的最小面积。

甲

乙

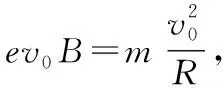
【点评】本题用到了磁发散规律，解题的关键是画好初速度沿x轴正方向及沿y轴正方向的电子运动轨迹，利用几何知识确定好磁场圆的圆心及半径。学生要准备好圆规、尺子、铅笔等作图工具进行规范作图，这有利于直观呈现题目，快捷准确找出数理关系。

【例2】如图5，ABCD是边长为a的正方形。质量为m、电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射，都只能从A点射出磁场。不计重力，求：

(1)此匀强磁场区域中磁感应强度的方向和大小；

(2)此匀强磁场区域的最小面积。

图5

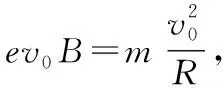
图6

【点评】本题是一个典型的磁聚焦考题，该题考查了学生对于带电粒子在磁场中运动的综合分析能力，重点考查了粒子运动的轨迹。这要求我们不仅要熟悉磁发散和磁聚焦规律中粒子在整个圆磁场区域运动情况，也要能在圆磁场局部区域运用所学规律。这要求同学们在学习中要善于分析，见微知著。

【例3】(2021·湖南卷第13题)带电粒子流的磁聚焦和磁控束是薄膜材料制备的关键技术之一。带电粒子流(每个粒子的质量为m、电荷量为+q)以初速度v垂直进入磁场，不计重力及带电粒子之间的相互作用。对处在xOy平面内的粒子，求解以下问题。

(1)如图7，宽度为2r1的带电粒子流沿x轴正方向射入圆心为A(0，r1)、半径为r1的圆形匀强磁场中，若带电粒子流经过磁场后都汇聚到坐标原点O，求该磁场磁感应强度B1的大小；

图7

(2)如图7，虚线框为边长等于2r2的正方形，其几何中心位于C(0，-r2)。在虚线框内设计一个区域面积最小的匀强磁场，使汇聚到O点的带电粒子流经过该区域后宽度变为2r2，并沿x轴正方向射出。求该磁场磁感应强度B2的大小和方向，以及该磁场区域的面积(无需写出面积最小的证明过程)；

(3)如图8，虚线框Ⅰ和Ⅱ均为边长等于r3的正方形，虚线框Ⅲ和Ⅳ均为边长等于r4的正方形。在Ⅰ、Ⅱ、Ⅲ和Ⅳ中分别设计一个区域面积最小的匀强磁场，使宽度为2r3的带电粒子流沿x轴正方向射入Ⅰ和Ⅱ后汇聚到坐标原点O，再经过Ⅲ和Ⅳ后宽度变为2r4，并沿x轴正方向射出，从而实现带电粒子流的同轴控束。求Ⅰ和Ⅲ中磁场磁感应强度的大小，以及Ⅱ和Ⅳ中匀强磁场区域的面积(无需写出面积最小的证明过程)。

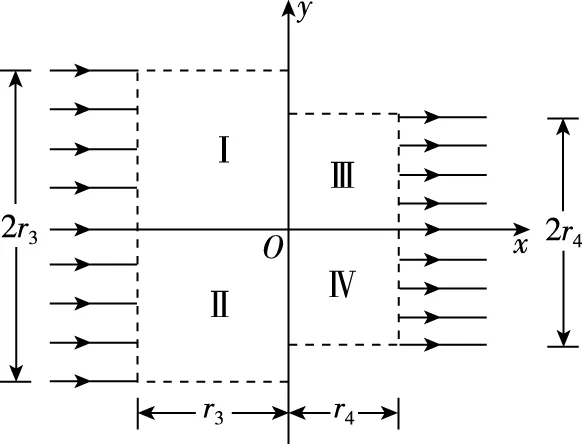
图8

图9

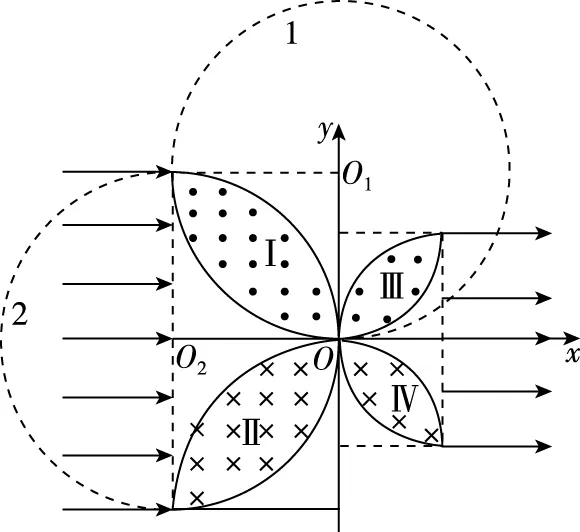
图10

【点评】本题是湖南省2021年高考计算题，本套试卷整体难度较大，学生作答的时间紧，而本题又有近五百字和两个图，学生阅读理解也需花费较多时间，题目综合用到了磁发散和磁聚焦两个规律，解题时既要用到物理中的洛伦兹力、圆周运动知识，又要用到数学中的平面几何知识，综合性较强，学生容易失分，但如果有了例题1和例题2的铺垫，学生解题时会游刃有余，从容面对，在紧张而紧凑的高考中节省宝贵时间，提升信心、稳定心态。