带电粒子在电磁组合场中运动规律探讨——对2021年全国高考物理甲卷第25题的深入剖析

安徽 王伟民 杨培军

带电粒子在磁场、电场特别是二者组合场中的运动规律问题，是近几年物理高考的热点问题，几乎每年的高考试卷都有此类问题出现，而且大多是综合性较强的计算题，在整个试卷中所占分值比例往往较高。这类综合性问题，可以考查学生对洛伦兹力、电场力、抛体运动、圆周运动等知识点的掌握情况，还可以考查学生综合运用物理知识解决复杂问题的能力。刚刚过去的2021年全国高考物理甲卷也是如此，下面的例题1就是该试卷的压轴题，单题分值高达20分。

一、原题呈现

【例1】(2021·全国甲卷第25题)如图1，长度均为l的两块挡板竖直相对放置，间距也为l，两挡板上边缘P和M处于同一水平线上，在该水平线的上方区域有方向竖直向下的匀强电场，电场强度大小为E；两挡板间有垂直纸面向外、磁感应强度大小可调节的匀强磁场。一质量为m，电荷量为q(q>0)的粒子自电场中某处以大小为v0的速度水平向右发射，恰好从P点处射入磁场，从两挡板下缘Q和N之间射出磁场，运动过程中粒子未与挡板碰撞。已知粒子射入磁场时的速度方向与PQ的夹角为60°，不计重力。

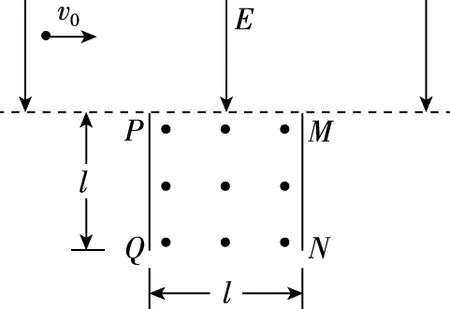
图1

(1)求粒子发射位置到P点的距离；

(2)求磁感应强度大小的取值范围；

(3)若粒子正好从QN的中点射出磁场，求粒子在磁场中的轨迹与挡板MN的最近距离。

二、试题评析

该题目共设置三个问题，三个问题彼此独立，考查的知识点全面而不重复，各问题的解决互不影响，这样可以避免考生因为前面的问题无法求解而影响后续问题解答的现象发生，使得试题的区分度更加的精细准确。否则，如果题目设置的多个问题互相牵连，前面问题的答案是解决后续问题的条件，那么，具有解答后续问题能力而前面问题没能正确解答的考生，做这样的题目将无法得分，这样对知识点掌握不全面和完全没掌握的考生就无法形成区分。

从考生反馈的消息来看，三个问题的难度也不相同，相比而言，第一个问题难度最大，考生只有熟练且灵活掌握平抛运动的规律和相关公式(包括运动学、动力学、电磁学的相关公式)，才有可能解决这个问题；第三个问题相对难度最低，但也需要考生具有正确判断带电粒子运动轨迹能力的同时，还要具有综合运用数学知识解决复杂物理问题的能力。

由此可见，本题目考查的知识点全面而有梯度，具有拉开不同水平和能力的考生分数差距的作用，这也是作为选拔性考试的试卷所必须具备的一个条件。

三、题目变式

带电粒子在电场与磁场的组合场中运动时，涉及电场强度、磁场强度、粒子质量、粒子电荷量、粒子的运动速度、轨迹圆的半径等诸多物理量以及有界电场或磁场的边界形状等条件，将这些物理量和相关条件作为常量或变量进行不同组合，可以归纳出种类繁多的问题，适合于编拟难度较大，技巧性较高的综合性推理计算或证明题目，此类问题大多需要结合数学知识方能解决，可以全面考查学生分析问题和解决问题的能力。如果我们以上面例题1给出的材料背景为蓝本，更改相关条件之后，可以将其改编为与原高考题目物理背景相似的变式题目。

由原高考题目条件可知，带电粒子在上方电场中的运动为类平抛运动，而它以一定速度由上方的电场进入下方磁场后的运动是匀速圆周运动，受电场和磁场边界形状的影响，粒子在组合场中的运动轨迹是一段抛物线与一段圆弧组合成的曲线。如果我们将题目对磁场的限制条件——磁场是“磁感应强度大小可调节的匀强磁场”更改为“磁场方向可作周期性变化的匀强磁场”，并限定其变化周期，那么带电粒子由上方的电场进入下方的磁场之后，它的运动轨迹将变得复杂起来，不再是原来的一段圆弧，而是多个相切的圆弧，这个问题的解决也将变得相对复杂。

图2

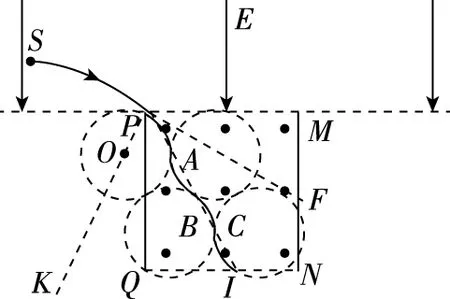
图3

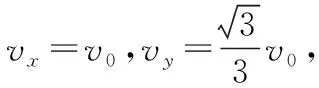
对原高考题目而言，为了使问题简化，题目限定了带电粒子的运动范围——“运动过程中粒子未与挡板碰撞”，而且粒子是“从两挡板下缘Q和N之间射出磁场”，所以带电粒子在磁场中的运动轨迹只能是一段圆弧。实际上，在不考虑粒子重力影响的情况下(不论是跟电场力、磁场力相比，还是跟粒子与挡板的作用力相比，在场强较大时，粒子的重力都是相对非常小的，通常可以忽略不计)，粒子与光滑挡板碰撞后的运动，其速度方向的改变也遵从光的反射定律，即反弹前后带电粒子的运动方向与挡板的夹角相等。因此，如果我们改变题目条件，人为的设定条件让粒子在磁场中与光滑挡板碰撞，那么，粒子在磁场中的运动轨迹也将不再是原来的一段圆弧，而是多段圆弧组合而成的曲线，这样一来，跟原来高考题目问题的求解过程相比，就需“额外”应用圆与圆之间的关系等几何知识，相关物理问题的解决难度也会相应增加。

图4

【分析】不计粒子重力时，带电粒子在有界磁场中的运动轨迹是圆或圆上的一部分(即圆弧)。由题目条件可知，带电粒子的运动分三个阶段——先在上面的电场中做类平抛运动，之后进入下面的磁场，在磁场中由于跟挡板撞击后再反弹，粒子沿一系列圆弧轨迹运动，最后由下面的磁场进入上面的电场做类斜抛运动。由于P、M关于HT对称，S、S′也关于HT对称，所以，粒子在M点离开磁场进入电场时的速度方向所在的直线，与它在P点由电场进入磁场时的速度方向所在的直线也关于HT对称。用反证法可以证明，带电粒子与挡板的4次碰撞的分布，只可能是与两个竖直挡板各碰撞一次，与底部的水平挡板碰撞2次，所以，粒子在磁场中的运行轨迹如图5所示。图5中只画出了粒子在磁场中的运动轨迹，粒子在上面电场中的运动轨迹没有画出。

图5

【解析】带电粒子在磁场中经过各挡板反弹后运动时，由于碰撞过程没有能量损失，所以，粒子在磁场中运动的速度大小保持不变，运动轨迹是半径相等的一系列圆弧，设圆弧的半径为r，图5中A、B、C、D是粒子在磁场中四次碰撞的反射点，易知，圆弧PA所对的圆心角为120°，所以：

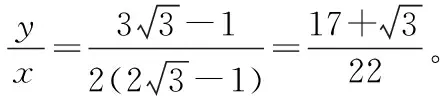
四、结语

带电粒子在电场和磁场形成的组合场中的运动，规律相对比较复杂。对带电粒子在组合场中运动规律的探讨，往往涉及多个物理知识点，问题的解决大多牵扯到很多物理公式，综合性很强，解决此类问题需要学生具有较强的分析问题和解决问题的能力，历年高考中，编者常将这类问题编拟为区分考生能力高下的压轴题的做法也就不足为奇了。

对原创题目进行改编是理科教师应该具备的一项基本技能。对于带电粒子在组合场中的运动问题，因为涉及的条件往往很多，可以改变条件与问题的组合进行变式改编，也可以将某个已知条件进行适当变化，如更改磁场或电场的边界形状，更改磁场或电场强度及方向的变化规律等，正所谓牵一发而动全身，当题目条件改换时，题目背景可能会发生质的改变。对一些高考原创题目进行改编，能够得到与原高考题目背景材料相似的变式题目，通过这样的改编，可以使我们对题目的条件与结论之间的逻辑关系，以及各并列条件之间的自洽关系有更为深入的理解。